Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

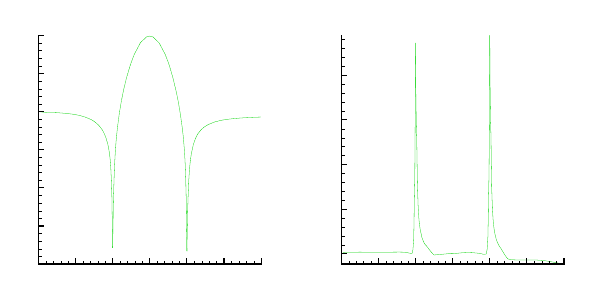
The results along the lower wall for a polynomial degree N = 4, integration order

P = 5, are displayed in Fig. 15. This ﬁgure shows that the resolution of the stagnation

points is very pronounced and the ﬂow almost retains its inﬂow Mach number after

the bump. The entropy change remains very small over the bump and the artiﬁcial

entropy increase is restricted to the location of the stagnation points.

0 0.5 1 1.5 2 2.5 3

0.1

0.2

0.3

0.4

0.5

0.6

0.7

(a) Mach number

Entropy

0 0.5 1 1.5 2 2.5 3

0.005

0.01

0.015

0.02

(b) Entropy

Fig. 15 The Mach number and entropy distribution for the subsonic ﬂow on a reﬁned mesh

6.1.2 Results for transonic ﬂow

To investigate the transonic ﬂow over a bump the geometry is the same as that for

the transonic ﬂow problems described by Spekreijse, [78], and Rizzi and Viviand,

[76].

As in the subsonic case, the chord length of the bump is c = 1. The length of the

channel however, is 5 times the chord length and the height is set at 2.073 times the

chord length. The height of the bump is 4.2% of the chord length. The mesh used

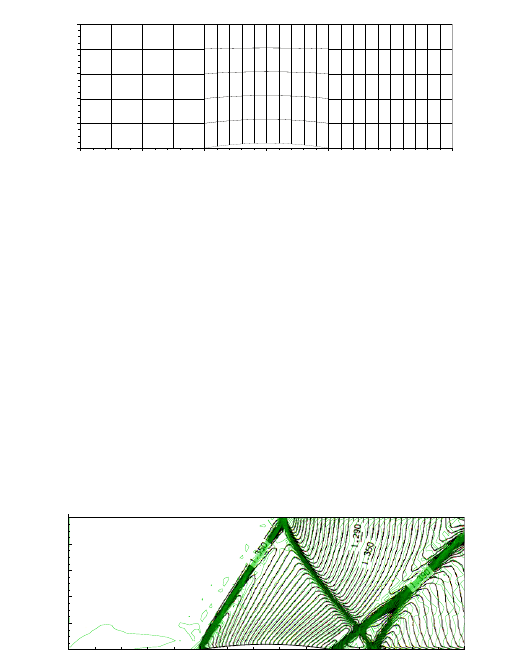
for this test case is shown in Fig. 16. The polynomial degree is N = 5 whereas the

integration order is P = 6.

In Fig. 17 the Mach contours at an inﬂow Mach number of M = 0.85 are com-

pared to the ﬁnite volume results produced by Spekreijse, [78].

The shock is positioned at approximately 86% of the bump with the Mach num-

ber just upstream of the shock being M ≈ 1.32. These results are quantitatively in

agreement with the ﬁnite volume results obtained by Spekreijse. In Fig. 18 the Mach

number distribution along the lower wall of the channel is shown.

203

Marc Gerritsma and Bart De Maerschalck

0 1 2 3 4 5

0.5

1.5

Fig. 16 The mesh used for the transonic test case. The height of the bump is 4.2% of the chord

length and 100 elements are used.

0 1 2 3 4 5

0.5

1.5

0 1 2 3 4 5

0.5

1.5

Fig. 17 Iso-Mach lines for transonic ﬂow, M = 0.85, obtained by LSQSEM (green) and Finite

Volume Method by Spekreijse [78], (black)

0 1 2 3 4 5

0.5

0.6

0.7

0.8

0.9

1.1

1.2

1.3

1.4

1.5

Fig. 18 Mach number distribution along the lower wall of the channel for a M = 0.85 ﬂow:

LSQSEM solution (green line) and Finite Volume results obtained by Spekreijse, [78], (black line)

204

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

6.1.3 Results for supersonic ﬂow

The geometry used for the supersonic test case is similar to that considered for the

subsonic ﬂow test case. The only difference is the height of the bump which is 4%

of the chord length for this test case. The mesh has a total of 120 elements as can be

seen in Fig. 19.

0 0.5 1 1.5 2 2.5 3

0.2

0.4

0.6

0.8

Fig. 19 The mesh used for the supersonic test case. The height of the bump is 4% of the chord

length and 120 elements are used.

At inﬂow the density is set to

= 1.4 and the pressure to p = 1. The Mach

number at the inlet boundary is M = 1.4.

At the leading edge of the bump a shock develops and runs into the domain until

it is reﬂected by the upper wall. From the trailing edge a shock originates at a slightly

smaller angle than the shock at the leading edge. In the region behind the bump the

two shocks collide and then merge into a single shock. The iso-Mach contours for

this test case are shown in Fig. 20 together with the results obtained by Spekreijse,

[78]. This ﬁgure reveals that the shock structures agree.

0 1 2 3

0.2

0.4

0.6

0.8

0 1 2 3

0.2

0.4

0.6

0.8

Fig. 20 Iso-Mach lines and shock structure obtained by LSQSEM (green) and Finite Volume

Method by Spekreijse [78], (black)

205

Marc Gerritsma and Bart De Maerschalck

7 Miscellaneous topics

In this section several topics will be discussed which improve the performance of

LSQSEM.

7.1 hp-adaptive LSQSEM

Although the combination of the least-squares formulation and the spectral ele-

ment technique leads to a very robust scheme which does not require any form

of stabilization and renders highly accurate solutions, using high order polynomi-

als throughout the entire computational domain is very expensive. The following

procedure is described in [33].

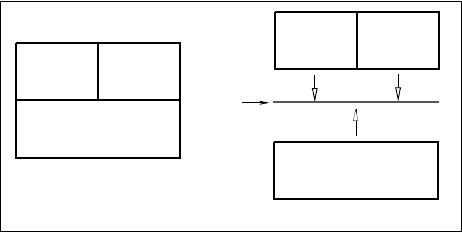
7.1.1 The mortar element method

Mortar

Computational domain

Ω

Fig. 21 The mortar element approach - patching the element edges with one

approximation space

In the mortar element method (MEM), neighbouring elements in R

are patched

together by mortar-like elements in R

d−1

. In R

the mortar elements consist of line

segments as sketched in Fig. 21. The i

boundary of element k, denoted by

, is

associated with a number of mortars,

. The solution on the mortars,

, is connected

to the solution at the border of the two neighboring elements. This establishes a

connection between the solution at the edge of an element, denoted by u

, and the

mortar solution

. If we choose a polynomial approximation for

on the mortar, we

can express the expansion coefﬁcients at the boundary of the element, u

, in terms

of the expansion coefﬁcients of the solution on the mortar,

, as

. (76)

206

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

The precise relation is inconsequential as long as the matrix

Z is of full rank for

at least one of the elements associated with the mortar. This condition prevents the

appearance of spurious mortar solutions.

Having established the relation between the elemental boundary unknowns and

the mortar unknowns, we can express the global system in terms of the inner element

unknowns, u

and the mortar unknowns

only:







Z 0

0 I





˜u

, (77)

where ˜u

represents the true unknowns, i.e. the projected mortar values and the

internal unknowns.

This transformation converts the least-squares formulation into

WLu

= L

⇐⇒

˜u

. (78)

Assembling all element contributions by summing over the projected element ma-

trices gives the global system to be solved.

In this paper the solution on the mortar is deﬁned by an L

-projection of the

element boundary solution

(u|

Ω

−

)

ds = 0, ∀ sides l and k = 1,.. .,K , (79)

where

∈P





and M is the polynomial degree of the mortar solution. M should

be greater than or equal to the degree of the solution in the adjoining elements to

prevent spurious mortar solutions. When the Lagrangian basis functions, deﬁned in

Section 3, are employed, the vertex condition (Maday et al. [56]) is automatically

satisﬁed. For a more extensive treatment of the mortar element method the reader is

referred to [48, 56].

7.1.2 The error estimator

Having discussed how to match spectral elements with different size and polyno-

mial representation, we now have to ﬁnd a way to detect those elements that need

reﬁnement.

In the least-squares formulation we select the solution which minimizes the resid-

ual globally over the whole domain

Ω

. Having obtained such a minimizing solution

we can evaluate the least-squares functional locally over every sub-domain A ⊂

Ω

This gives

= kL u

− f k

(A)

= kL



−u



(A)

, (80)

due to the linearity of L . Well-posedness of the problem (30) then implies that

kek

X(A)

≤

≤C

kek

X(A)

, (81)

207

Marc Gerritsma and Bart De Maerschalck

where e = u

−u

. This means that the effectivity index

A,X

, deﬁned by

A,X

kek

X(A)

, (82)

which compares the estimated error

to the exact error in the X-norm is bounded

≤

≤C . (83)

Alternatively, we may compare the estimated norm

with the residual norm

kRk

(A)

using the fact that the residual norm is norm equivalent to kek

. Denot-

ing this effectivity index by

A,R

gives the rather trivial result

A,R

kL u

− f k

Y(A)

≡ 1 . (84)

Based on this observation

will be used to identify those regions (elements in

case A =

Ω

) which are selected for reﬁnement. This estimator has also been used

by Liu, [54] and Berndt et al., [4].

7.1.3 Estimation of the Sobolev regularity

Having found a way to match functionally and geometrically non-conforming ele-

ments and an indicator

Ω

which ﬂags elements for reﬁnement, we now have to

determine how to reﬁne. This choice is based on the smoothness of the underlying

exact solution. If the exact solution is locally sufﬁciently smooth, polynomial en-

richment is employed. However, if on the other hand, the underlying exact solution

has limited smoothness h-reﬁnement is used.

Let

be a spectral element with size parameter h

and polynomial degree p

Let u

be the exact solution in that element, where u

∈H

, where k

≥0 denotes

the Sobolev regularity of the exact solution. Let u

denote the LSQSEM solution

with u

∈ H

, 0 ≤ q ≤k

then

−u

≤C

)

−q

)

−q

, (85)

where s

= min(p

+ 1,k

) and C is a generic constant. This error estimate tells

us that if the solution is very smooth (k

very large) then the error decreases more

rapidly by increasing p

in the denominator. For practical purposes the function

is considered smooth if k

> p

+ 1 and non-smooth when k

≤ p

+ 1, in which

h-reﬁnement is more effective.

So the choice between h-reﬁnement and p-enrichment is dictated by the Sobolev

index of the exact solution. Although the exact solution is in general not available,

we can still estimate this index from its numerical approximation. Houston et al.,

[50] have developed a method to estimate the Sobolev index from a truncated Leg-

208

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

endre series. They assume that the one-dimensional solution is in L

(−1,1) which

allows for a Legendre expansion

u(x) =

∞

∑

i=0

(x) , with a

2i + 1

−1

u(x)L

(x)dx . (86)

By Parseval’s identity the fact that u ∈L

(−1,1) is equivalent to convergence of the

series

∞

∑

i=0

2i + 1

. (87)

In [50] it is shown that if

∞

∑

i=[k+1]

2i + 1

(i + k + 1)

(i −k + 1)

, (88)

converges, then u ∈H

(−1,1), where

(

u ∈ L

(−1,1)



∑

j=0

−1



( j)

u(x)





1 −x



dx < ∞

)

, (89)

for integer values of k. By using the

-function in (88) this identity can be extended

to fractional Sobolev spaces, see [50] for details.

Given the Legendre coefﬁcients a

, convergence of the series in (88) can be es-

tablished by well-known techniques such as the ratio test, or the root test.

In this work the root test is employed. This leads to the calculation of

log



2k+1

2|a



2logk

. (90)

If l = lim

k→∞

> 1/2 then u ∈ H

l−1/2−

(−1,1), ∀

> 0. Else u ∈L

(−1,1). Since

in a numerical solution only a ﬁnite number of Legendre coefﬁcients a

are available,

this test is applied to the highest Legendre coefﬁcient available in the numerical

approximation. Based on the estimated Sobolev index l −1/2, the decision is made

whether to reﬁne the mesh, or to increase the polynomial degree locally.

This one-dimensional estimate of the Sobolev index can be extended to multi-

dimensional problems by treating each co-ordinate direction separately, see [50] for

details. Several tests have been performed to establish the validity of this estimator.

Proposition 1. If an element

at reﬁnement level r with characteristic mesh size

and polynomial degree p

is ﬂagged for reﬁnement by the error indicator, we

calculate l

by (90). Then for the Sobolev index k

= l

−1/2 we have







If k

> p

+ 1 then p

r+1

← p

+ 1 .

If k

≤ p

+ 1 then h

r+1

← h

/2 .

(91)

209

Marc Gerritsma and Bart De Maerschalck

7.1.4 Application to the space-time linear advection equation

This section uses the one-dimensional, linear advection problem to validate the pre-

sented hp-adaptive theory. The application of LSQSEM to hyperbolic equations has

been studied by De Maerschalck, [18, 19, 20, 21].

The model problem is deﬁned as

∂

+ a

∂

= 0 with 0 ≤ x ≤ L, t ≥ 0, a ∈R (92)

u(0,t) = 0 , (93)

u(x,0) =











−

cos



x−x



if x

≤ x ≤ x

+ L

0 elsewhere .

(94)

where a is the advection speed and L is the length of the domain in spatial direction.

On the left boundary of the domain a Dirichlet boundary condition, u(0,t) = 0, is

imposed. The initial disturbance, u(x,0), is a cosine-hill with offset x

and width L

We use a space-time formulation that treats the one-dimensional advection problem

0 0.5 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Fig. 22 Illustration of the unstructured mesh and continuous propagation of

the cosine-hill with hp-reﬁnement

with a two-dimensional least-squares formulation and considers the time variable t

210

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

as second spatial variable. Instead of calculating the solution over the whole domain

at once, we use a semi-implicit approach. The domain is subdivided into several

space-time strips for which the solution is approximated using the LSQSEM, see

[20] for details. In the following, 32 time strips are used within the domain

Ω

[0,1], where each time strip has initially 32 cells. Each time strip uses the solution at

the previous strip as initial condition, except for the ﬁrst strip that uses the prescribed

initial condition (94). All time strips use the Dirichlet condition (93) on the left

boundary. The advection speed a = 0.85, x

= 0.13 and L

= x

+ 0.5. The exact

solution of this problem u

∈ H

5/2−

(

Ω

), for all

> 0. The regularity of the exact

solution is limited in space-time over the lines x−at = x

and x −at = x

+ L

. For

all other points in the space-time domain the solution is inﬁnitely smooth.

7.1.5 Illustration of an hp-adaptive strategy

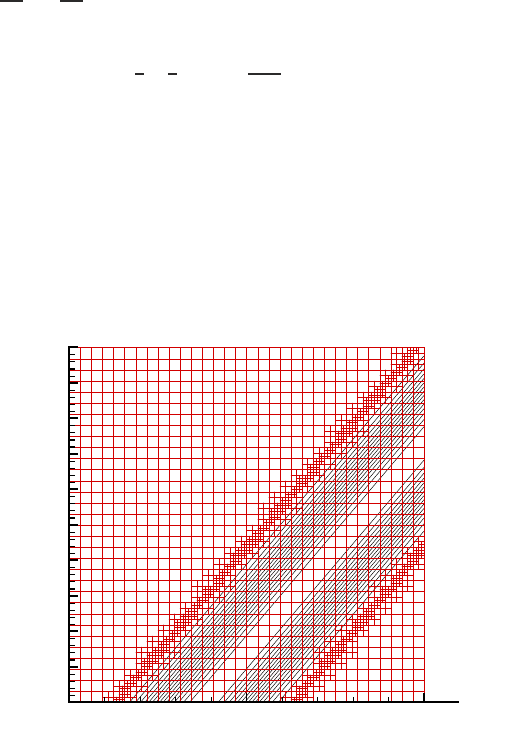
Note that even though only the second derivative is discontinuous, the regularity

estimator accurately identiﬁes the region with limited regularity as depicted in Fig-

ure 22. No h-reﬁnement is used in the smooth parts of the domain.

0 0.5 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Fig. 23 Polynomial degree distribution for hp-adaptivity within each element

Figure 23 shows the ﬁnal polynomial degree distribution. We imposed the so-

called 1-level adaptivity, where the difference in reﬁnement level between neigh-

bouring elements may not be more than one. In the regions where the exact solution

211

Marc Gerritsma and Bart De Maerschalck

is zero neither p-enrichment nor h-reﬁnement is used. Along the cosine hill polyno-

mials of degree N = 4 are used, the green strip. The only place where the algorithm

uses higher order elements is along the lines with limited regularity. Along these

lines both p-enrichment and h-reﬁnement are employed.

The reason high order elements are used along these lines is that in order to pre-

dict the Sobolev regularity accurately enough, one needs sufﬁciently high Legendre

coefﬁcients.

7.2 Direct Minimization

In this section an alternative method will be described which minimizes the residual

directly in contrast to the conventional least-squares formulation where one employs

variational analysis to set up the weak formulation. The resulting condition number

is only the square root of the condition number that would be obtained if the conven-

tional least squares method had been used. In addition, the new method circumvents

a costly matrix-matrix multiplication thus avoiding loss of precision and ﬁll-in in

the stiffness matrix. This approach is also described in [49].

7.2.1 Conventional least-squares ﬁnite element method

In Section 2 and 3 the approach for the conventional or variational least-squares

formulation is described. This approach can be summarized as

(L (u),L (v)) = ( f,L (v)) ⇐⇒

Ω

L (u)L (v)d

Ω

f L (v)d

Ω

∀v ∈X(

Ω

) .

(95)

The next step consists of domain decomposition where the integration over

Ω

written as the sum of the integrals over the sub-domains

Ω

, k = 1,.. .,K,

∑

Ω

L (u)L (v)d

Ω

∑

Ω

f L (v)d

Ω

∀v ∈ X(

Ω

) . (96)

∑

N,k

Ω

L (

)L (

Ω

∑

Ω

f L (

Ω

∀

, j = 1, ..., N .

(97)

It sufﬁces in (97) to take v =

, because L is assumed to be a linear operator and

since any arbitrary v in the ﬁnite-dimensional subspace is a linear combination of

these basis functions.

Inserting the Gauss-Lobatto integration then gives

212

N,k

∑

N,k

(x),

where the

are basis functions, which span the ﬁnite-dimensional subspace over

Ω

Then we insert the ﬁnite-dimensional approximation for each element u