Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

(a) (b)

Fig. 2 Types of ﬂow for low Re numbers, Re < 6 (a) and Re > 6 (b)

Fig. 3 Flow characteristics for a low Re ﬂow around a circular cylinder

5.5 Comparison of numerical data with experimental data

Results of Taneda [81], Coutanceau [17] and Tritton [82] are used to benchmark the

results of LSQSEM.

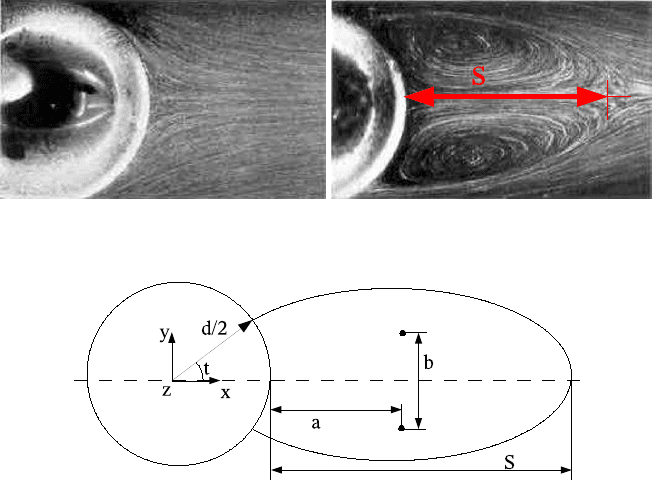
5.5.1 S/d: LSQSEM vs. Experiment

The LSQSEM values are compared to experimental values from Coutanceau and

Taneda in Table 1. The same data are depicted in Fig. 4. For the LSQSEM simula-

tions a mesh consisting of 62 elements was used with varying polynomial degree.

The LSQSEM results given in Fig. 4 were obtained with polynomial degree P = 10

in both x- and y-direction. This corresponds to an 11th-order scheme.

The Onset Reynolds number The onset Reynolds number is the lowest Reynolds

number for which the twin vortices behind the cylinder can be observed. By using

polynomials of degree N = 10, Re

onset

is sought on the mesh where symmetry is

explicitly imposed. Fig. 5 displays S/d for various Reynolds numbers.

Vortex center The vortex center, of which the location is indicated by a and b

in Fig 3, is also a property commonly investigated for this type of ﬂow. The result

for a and b can be found in Table 3 for the simulations as well as the experimental

values of Coutanceau [17].

193

Marc Gerritsma and Bart De Maerschalck

Table 1 Recirculation length S/d for

LSQSEM and data from Coutanceau

Re S/d

Groot Coutanceau Taneda

10 0.27 0.34 0.3

20 0.94 0.93 0.9

30 1.57 1.53 1.5

40 2.17 2.13 2.1

Re [-]

S/d [-]

5 10 15 20 25 30 35 40 45

0.5

1.5

Groot, P10

Coutanceau

Taneda

Fig. 4 Recirculation length S/d form LSQSEM and data form Coutanceau

Table 2 Recirculation length S/d, obtained by the least squares method and other numerical meth-

ods

Re S/d

Groot Groot Den & Shi Kaw & Jai Tak & Kel Nie & Kel

2003 1965 1966 1969 1973

10 0.27 0.25 0.56 0.3 0.25 0.217

20 0.94 0.88 1.06 1 0.935 0.803

30 1.57 1.44 1.16 1.75 1.611 1.543

40 2.17 1.94 0.94 2.515 2.325 2.179

194

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

S/d

5 5.5 6 6.5 7

0.01

0.02

0.03

0.04

0.05

0.06

0.07

S/d

Fig. 5 Recirculation length in the vicinity of Re

onset

Table 3 Position of vortex core as a function of Re

Re Groot, P = 10 Coutanceau

a b a b

10 0.12 0.24 0.12 0.32

0.35 0.44 0.33 0.47

0.53 0.52 0.55 0.54

0.68 0.58 0.76 0.59

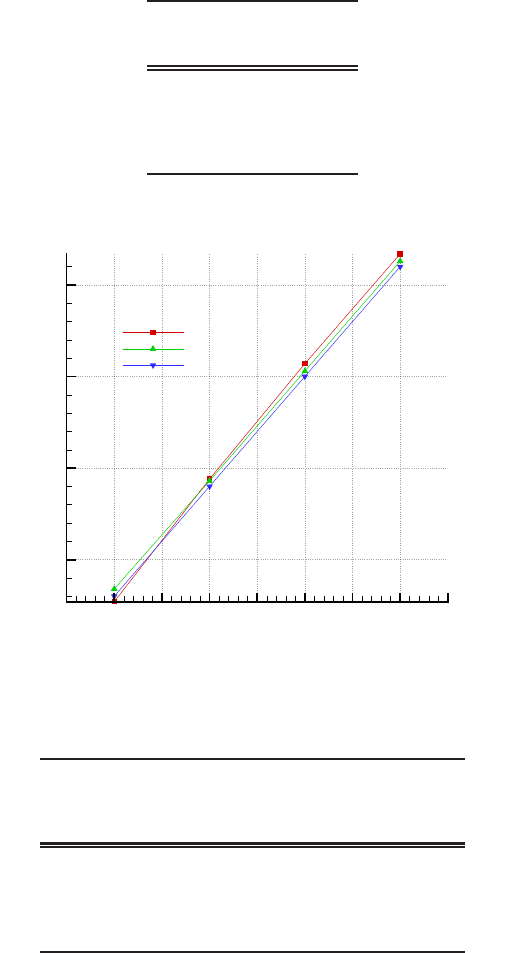
Separation angle The separation angle is also a characteristic of the ﬂow around

a circular cylinder. For the deﬁnition of the separation angle see Fig. 3. Table 4

shows the results for the separation angle in the range, 10 ≤Re ≤40, for two differ-

ent settings. Table 4 shows in the third column the experimentally obtained values

of Coutanceau [17].

Table 4 Separation angle as function of Re

Re Groot Coutanceau

P = 7 P = 10

10 29.75 30.14 32.5

43.50 43.93 44.8

49.57 49.90 50.1

53.38 53.77 53.5

195

Marc Gerritsma and Bart De Maerschalck

Drag coefﬁcient Besides the ﬂow ﬁeld features as separation angle and recircu-

lation length, also an integral quantity of the ﬂow is investigated, the drag coefﬁcient

Almost every textbook on the fundamentals of Aerodynamics gives ”accurate”

formulae to predictC

for a cylinder in uniform parallel ﬂow. Let us investigate how

well the least squares solution matches these curve ﬁtted formulae. The ﬁrst formula

is derived by Tritton [82] and valid around Re ≈1.0,

≈ 1 +

10.0

2/3

. (62)

The second formula, from Sucker and Brauer [80], is valid over a much wider range,

−4

< Re < 2.0 ·10

≈ 1.18 +

6.8

0.89

1.96

−

0.0004 ·Re

1 + 3.64 ·e −7 ·Re

. (63)

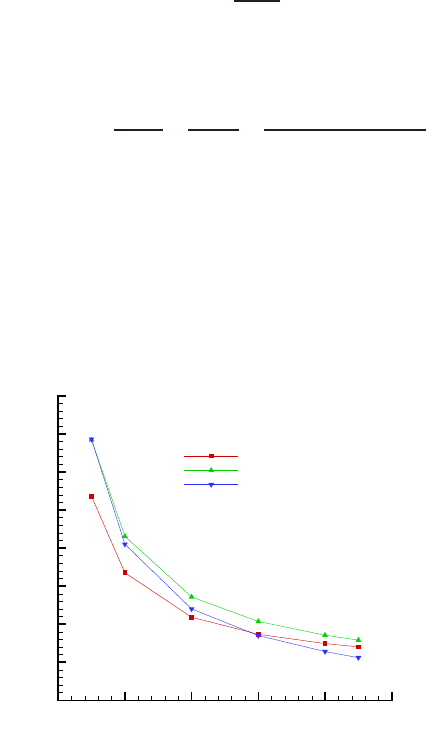
White [83] emphasizes the good accuracy of (63). Fig. 6 shows the convergedresults

from the simulation together with the curve ﬁts. Despite the claimed accuracy of the

curve ﬁts a signiﬁcant gap with the numerical data emerges. To further investigate

the accuracy of the numerically obtained C

values, experimental data of Tritton

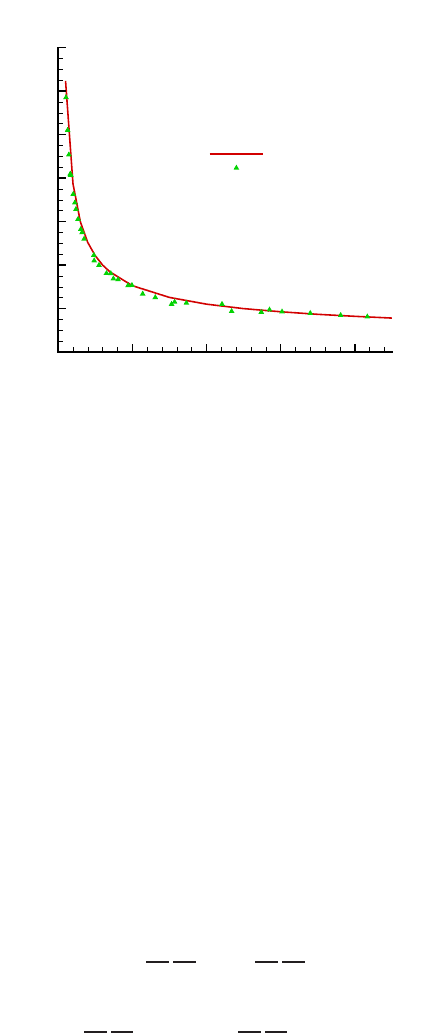
[82] was used. Fig. 7 shows the numerical results obtained with the least squares

method and the experimental results from Tritton [82] over the range: 1 ≤ Re ≤ 45.

Cd [-]

0 10 20 30 40 50

1.5

2.5

3.5

4.5

Sucker Brauer

Tritton

Groot, P=7

Fig. 6 Numerical results for C

and curve ﬁts form experimental data

196

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

Cd [-]

0 10 20 30 40

Groot, P7

Tritton

Fig. 7 Drag coefﬁcient (C

) from simulation and experiments

5.6 Unsteady ﬂow around a cylinder at low Reynolds

For time dependent ﬂows one can either employ time stepping methods or discretize

the system of governing equations in space-time. The latter approach was investi-

gated by De Maerschalck, [18, 19, 20, 21]. Kwakkel, [49, 53] performed a series of

numerical simulations for the ﬂow around a cylinder in a channel. A BDF3 scheme

was used for the time integration.

The ﬁnal test case is the periodic ﬂow around a moving circular cylinder in a

narrow channel. To be able to simulate the ﬂow around the cylinder, the cylinder is

ﬁxed and the channel is moved (change of reference frame). The boundary condi-

tions are u = 1 and v = 0 at the inﬂow and channel walls and a no-slip condition

(u = v = 0) at the cylinder surface. The outﬂow boundary condition is the same as

in the work of Pontaza, [58] and is described in Section 5.6.1.

5.6.1 Outﬂow boundary condition

The outﬂow boundary conditions are deﬁned as



−p +

∂



∂

= 0, (64)

∂



−p +

∂



= 0, (65)

197

Marc Gerritsma and Bart De Maerschalck

where n

and n

are the x and y-components of the outward unit normal along the

boundary. This boundary condition is enforced in a weak sense through the least-

squares functional, see (32).

Vortex shedding is described by the dimensionless Strouhal number

St =

f l

, (66)

where f is the frequency of the vortex shedding, l the characteristic length (diameter

of the cylinder) and V the free stream velocity of the ﬂuid. Pontaza, [58], reports a

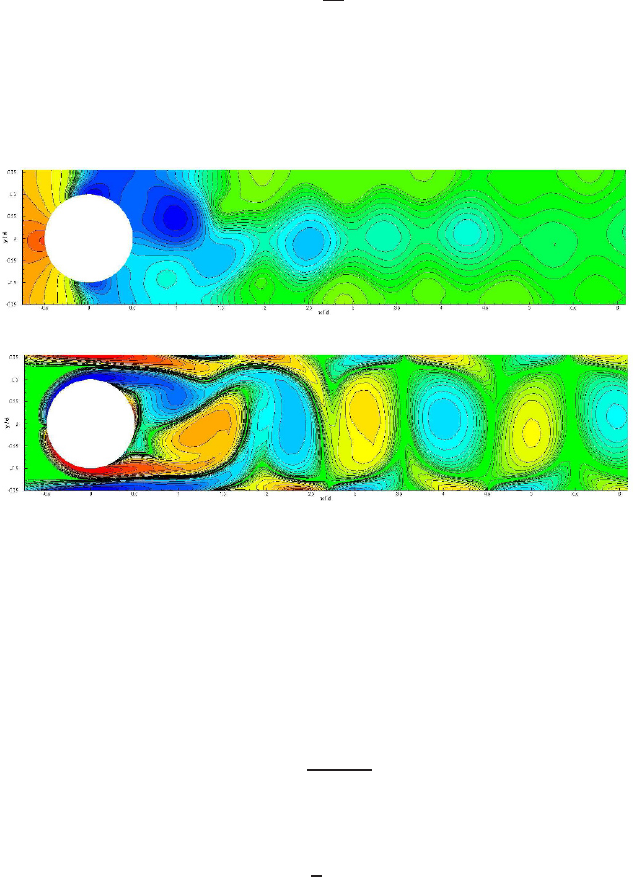
Strouhal number of St=1/1.88=0.5319, see Fig. 8. The Reynolds number was set to

Re = 100.

(a) Pressure contours.

(b) Vorticity contours.

Fig. 8 Instantaneous pressure and vorticity contours for P

= 8.

5.6.2 Base pressure coefﬁcient

The base pressure coefﬁcient C

is deﬁned by

− p

∞

, (67)

where p

is the base pressure, p

∞

the free stream pressure and where

∞

is the dynamic pressure.

198

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

0 1 2 3

4 5 6

−13.0

−12.8

−12.6

−12.4

−12.2

−12.0

Time

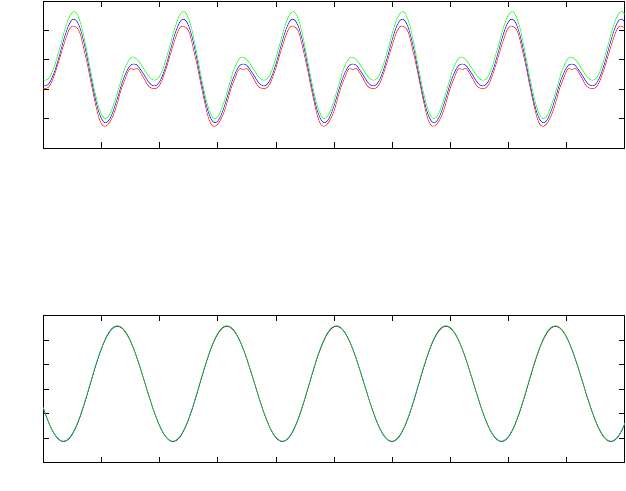
Fig. 9 Time history of C

P = 6 (red) P = 8 (blue) and the reference value from [58] with P = 6

(green)

Fig. 9 shows the time history of the base pressure coefﬁcient C

for two poly-

nomial degrees and the reference solution from [58].

5.6.3 Drag and lift coefﬁcients

The lift C

and drag C

coefﬁcients are often used to compare the results of the ﬂow

around a circular cylinder. These coefﬁcients are deﬁned by

∞

, C

∞

, (68)

where F is the force in the direction indicated, q

∞

the dynamic pressure and d the

diameter of the cylinder, which is equal to unity. The forces are calculated by

F = −

·d

, (69)

where

is the boundary of the cylinder and

the extra stress tensor. In components

this can be written as

= −

(

, (70)

= −

(

. (71)

The extra stress tensor for a Newtonian incompressible ﬂuid is

∂

, (72)

where

is the dynamic viscosity. For Re < 188 the ﬂow will be periodic in time,

so both C

and C

must be periodic. The frequencies of the drag and lift curves

both depend on the frequency of the vortex shedding. The frequency of the drag

199

Marc Gerritsma and Bart De Maerschalck

curve has twice the frequency of the lift curve however. This is because for the lift

it is important which vortex is shed off (top or bottom) and for the drag it is only

important if a vortex is shed. Comparison of Fig. 10 and 11 shows that this is the

case.

0 1 2 3 4

5 6

7 8 9 10

12.2

12.3

12.4

12.5

12.6

12.7

Time

Fig. 10 Time history of C

; P = 6 (red) P = 8 (blue) and the reference value from [58] with P = 6

(green)

0 1 2 3 4

5 6

7 8 9 10

−3.0

−2.0

−1.0

0.0

1.0

2.0

3.0

Time

Fig. 11 Time history of C

; P = 6 (red) P = 8 (blue) and the reference value from [58] with P = 6

(green)

Fig. 11 shows that the results for C

agree with the reference values. The fre-

quency that follows from (66) is St = 1/1.88 = 0.5319, which agrees with the value

of [58]. The value of 1.88 is obtained from the time history plot of the lift coefﬁcient

and is the time between two peaks, see Fig. 11.

6 Compressible ﬂows

Inviscid, compressible ﬂows may exhibit discontinuous solutions – shocks or con-

tact discontinuities. These solutions are not in H

(

Ω

) and therefore an H

-coercive

formulation is not possible. The proper functional setting for these problems is in the

weaker space H(div;

Ω

). Since in the ﬁnite-dimensional case all norms are equiva-

lent, one can still use the conventional least-squares approach but in this case opti-

mal convergence is not guaranteed.

200

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

Compressible ﬂows in the absence of dissipative terms are governed by the Euler

equations. There are several ways in which the Euler equations in differential form

can be written, but only the conservative form in terms of conserved quantities will

be presented.

The two-dimensional Euler equations in conservation form are given by

∂













∂







+ p







∂







+ p



















. (73)

These equations express conservation of mass, conservation of momentum in the x-

and y-direction and conservation of energy, respectively. Here

is the local density,

p is the pressure and (u, v) denotes the ﬂuid velocity. The total energy per unit mass

is denoted by E . The total energy can be decomposed into internal energy e and the

kinetic energy per unit mass

E =

e +



+ v



−1



+ v



, (74)

where in the last equality we assume a calorically ideal, perfect gas with

the spe-

ciﬁc ratio of heats of the gas.

6.1 Compressible ﬂow over a circular bump

In this section results are given for the ﬂow over a circular bump in a 2D channel.

Results will be given for subsonic ﬂow, M

∞

= 0.5, transonic ﬂow, M

∞

= 0.85 and

supersonic ﬂow, M

∞

= 1.4. This is a difﬁcult test problem over the entire Mach

range for spectral methods due to the presence of stagnation points at the leading

and trailing edge of the bump. See [38] for further details of this approach.

6.1.1 General geometry and boundary conditions

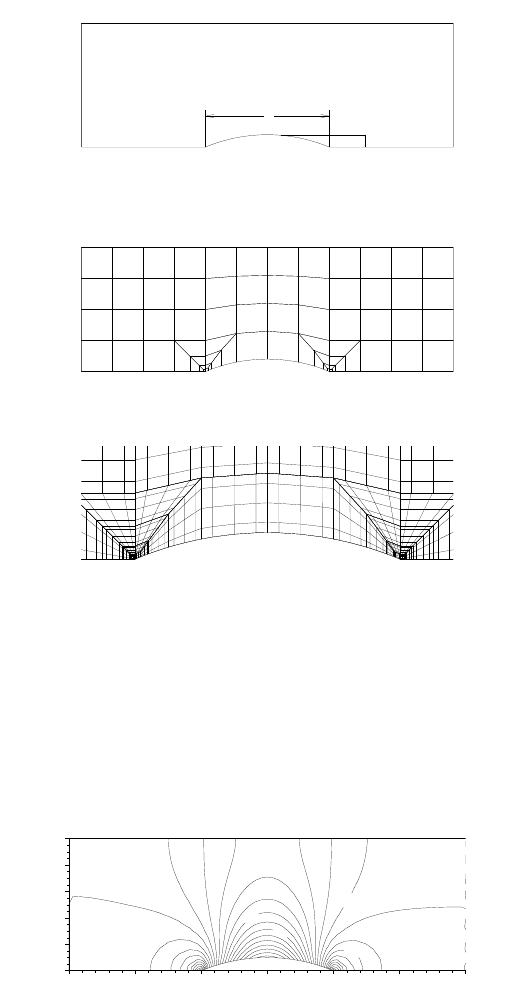
The general geometry for the channel ﬂow with a circular bump is shown in Fig. 12.

The bump is modeled by curved elements using the transﬁnite mapping by Gordon

and Hall, [40]. All length and height parameters of the channel will be scaled with

the chord length c of the bump.

The inﬂuence of the mesh is assessed by reﬁning the mesh around the stagnation

point. The reﬁned mesh consists of 72 elements, Fig. 13.

The entropy variation s in the domain is calculated with the freestream entropy

as a reference:

s =

ˆs − ˆs

∞

ˆs

∞

, where ˆs = p

−

. (75)

201

Marc Gerritsma and Bart De Maerschalck

Fig. 12 The general geometry of the 2D channel with a circular bump

(a) Mesh

(b) Details of mesh near the bump

Fig. 13 Reﬁned mesh near stagnation points consisting of 72 spectral elements of polynomial

degree N = 4. (a) Spectral element mesh, (b) close-up near the bump:spectral elements with Gauss-

Lobatto-grid

Pressure contours are given in Fig. 14.

0 0.5 1 1.5 2 2.5 3

0.2

0.4

0.6

0.8

Fig. 14 Pressure contours for the subsonic ﬂow

202