Korb K.B., Nicholson A.E. Bayesian Artificial Intelligence

Подождите немного. Документ загружается.

ALGORITHM 4.4

Decision Tree Evaluation

1. Starting with nodes that have only leaves (utility nodes) as children.

2. If the node

is a chance node, each outgoing link has a probability and each

child has an associated utility. Use these to compute its expected utility

If the node isa decision node, eachchildhas a utility or expected utility attached.

Choose the decision whose child has the maximum expected utility and

3. Repeat recursively at each level in the tree, using the computed expected utility

for each child.

4. The value for the root node is the maximal expected utility obtained if the

expected utility is maximized at each decision.

4.4.4 Value of information

The results of the decision tree evaluation are summarized in Table 4.3 (highest ex-

pected utility in each case in bold). We can see that the rational decision for Paul is to

have the inspection done, as the expected utility (which is the expected proﬁt in this

case) is 2635 compared to 2600 if the inspection is not done. Paul’s next decision,

as to whether to buy the house, will depend on whether he receives a good or bad

inspection report. If the report is bad, his decision will be not to buy, with expected

utility -600 compared to -2682 for buying. If the report is good, he will go ahead and

buy, with expected utility 4055 compared to the same -600 when not buying.

TABLE 4.3

Decisions calculated for the real estate investment problem

Evidence Bel(C=good) EU(I=yes) EU(I=no) Decision

None 0.70 2635 2600 I=yes

Given I=no EU(BH=yes) EU(BH=no)

Report=unknown 0.70 2600 0 BH=yes

Given I=yes EU(BH=yes) EU(BH=no)

Report=good 0.957 4055 -600 BH=yes

Report=bad 0.115 -2682 -600 BH=no

This is a situation where additional information may change a decision, as with-

out the test Paul would just go ahead and buy the house. The decision of whether

to gather information is based on the value of the information. The difference in

the expected utilities with and without the extra information is called the expected

beneﬁt. In general,

For our real estate example,

So, even if there is a cost associated with obtaining additional information (such as

the inspection fee), if the expected beneﬁt is greater than zero, the price is worth

paying.

4.4.5 Direct evaluation of decision networks

This decision tree evaluation method conveys the underlying ideas of evaluating de-

cision networks containing sequential decisions. We start with the ﬁnal decision and

calculate the expected utility for the various options, given the scenario that has been

followed to get there, and choose the decision with the maximum expected utility.

This is then repeated for the next-to-last decision, and so on, until the ﬁrst decision

is made.

However, expanding a decision network into a decision tree and using Algo-

rithm 4.4 is very inefﬁcient. Various methods have been developed for evaluating

decision networks (see Bibliographic notes in

4.8). Many are similar to the infer-

ence algorithms described in Chapter 3, involving compilation into an intermediate

structure, and propagation of probabilities and expected utilities (see [128, Chapter

7] for details). It is possible to avoid the repetitions of the same calculations that

we saw using decision tree evaluation, by taking advantage of the network structure.

However, all methods face the same complexity problem.

Thus far, we have only looked at sequential decision networks involving just two

decisions. There is no theoretical limit to how many sequential decisions can be

made. However, this leads us to the general problem of planning under uncer-

tainty, which once again is an exponential search problem, as the number of possible

plans is the product of the number of actions considered for each plan step.

4.5 Dynamic Bayesian networks

Bayesian and decision networks model relationships between variables at a partic-

ular point in time or during a speciﬁc time interval. Although a causal relationship

represented by an arc implies a temporal relationship, BNs do not explicitly model

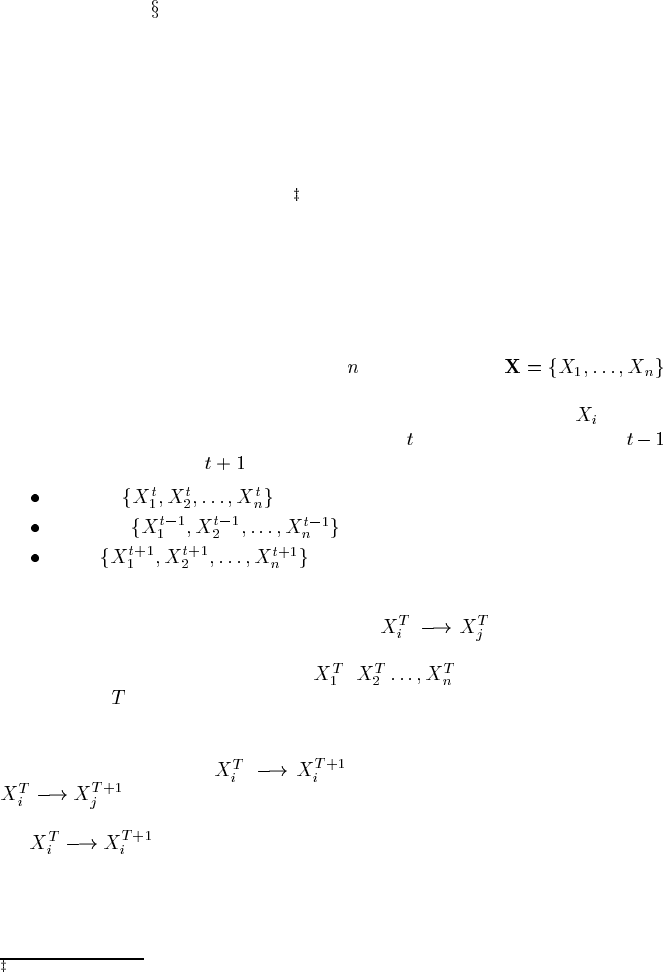
temporal relationships between variables. And the only way to model the relation-

ship between the current value of a variable, and its past or future value, is by adding

another variable with a different name. We saw an example of this with the fever

example earlier in

4.3.5, with the use of the FeverLater node. In the decision net-

works we have seen so far, there is an ad hoc modeling of time, through the use of

information and precedence links. When making a sequence of decisions that will

span a period of time, it is also important to model how the world changes during

that time. More generally, it is important to be able to represent and reason about

changes over time explicitly when performing such tasks as diagnosis, monitoring,

prediction and decision making/planning.

In this section we introduce a generalization of Bayesian networks, called dy-

namic Bayesian networks (DBNs)

, that explicitly model change over time. In

the following section we will extend these DBNs with decision and utility nodes, to

give dynamic decision networks, which are a general model for sequential decision

making or planning under uncertainty.

4.5.1 Nodes, structure and CPTs

Suppose that the domain consists of a set of random variables ,

each of which is represented by a node in a Bayesian network. When constructing

a DBN for modeling changes over time, we include one node for each

for each

time step. If the current time step is represented by

, the previous time step by ,

and the next time step by

, then the corresponding DBN nodes will be:

Current:

Each time step is called a time-slice. The relationships between variables in a

time-slice are represented by intra-slice arcs,

. Although it is not a

requirement, the structure of a time-slice does not usually change over time. That is,

the relationship between the variables

, is the same, regardless of

the particular

The relationships between variables at successive time steps are represented by

inter-slice arcs, also called temporal arcs, including relationships between (i) the

same variable over time,

, and (ii) different variables over time,

In most cases, the value of a variable at one time affects its value at the next, so

the

arcs are nearly always present. In general, the value of any node

at one time can affect the value of any other node at the next time step. Of course,

a fully temporally connected network structure would lead to complexity problems,

but there is usually more structure in the underlying process being modeled.

Also called dynamic belief networks [237, 206], probabilistic temporal networks [69, 70] and dy-

namic causal probabilistic networks [147].

Next time t+1Previous time t−1 Current time t

−

r−

t−1

t+1

t+2

FIGURE 4.10

General structure of a Dynamic Bayesian Network.

Figure 4.10 shows a generic DBN structure, with a sequence of the same static

BNs connected with inter-slice arcs (shown with thicker arcs). Note that there are no

arcs that span more than a single time step. This is another example of the Markov

assumption (see

2.2.4), that the state of the world at a particular time depends only

on the previous state and any action taken in it.

The relationships between variables, both intra-slice and inter-slice, are quantiﬁed

by the conditional probability distribution associated with each node.

In general, for node

with intra-slice parents , , and inter-slice par-

ents

and , , ,theCPTis

Given the usual restriction that the networks for each time slice are exactly the

same and that the changes over time also remain the same (i.e., both the structure and

the CPTs are unchanging),a DBN can be speciﬁed very compactly. The speciﬁcation

must include:

Node names

Intra-slice arcs

Temporal (inter-slice) arcs

CPTs for the ﬁrst time slice (when there are no parents from a previous

time)

CPTs for slice (when parents may be from or time-slices).

Some BN software packages provide a facility to specify a DBN compactly (see

B.4).

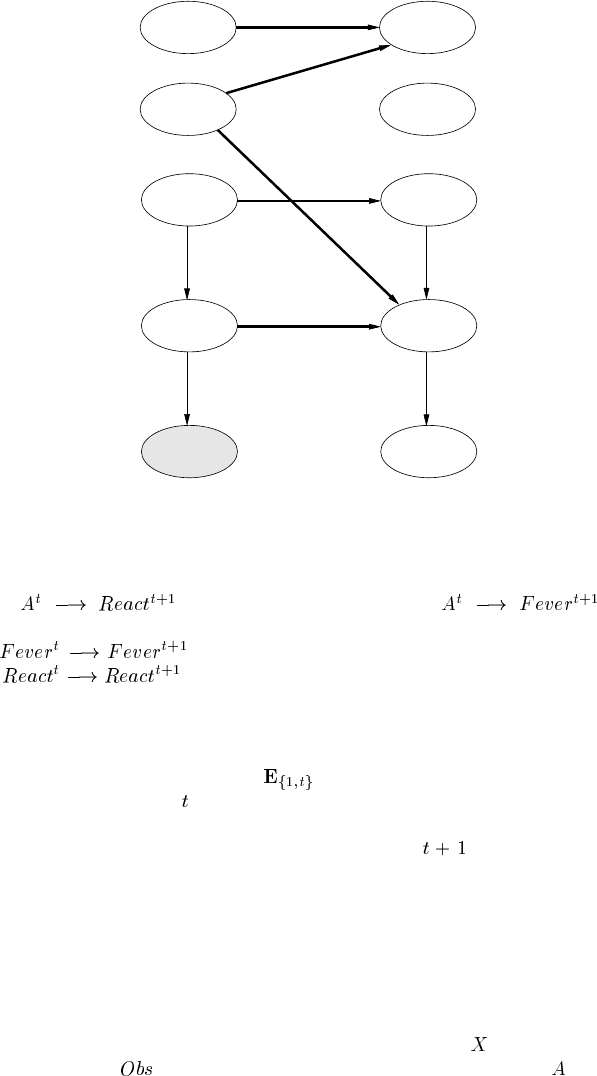
Figure 4.11 shows how we can use a DBN to represent change over time ex-

plicitly in the fever example. The patient’s ﬂu status may change over time, as

there is some chance the patient will get better, hence the

arc.

Taking aspirin at time

, indicated by , may produce a reaction at the next time

React

t+1

Flu

t+1

Fever

t+1

Fever

t+1

FIGURE 4.11

DBN for the fever example. (Shaded node indicates evidence added.)

step ( ) and it may reduce the fever ( ), al-

though the subsequent fever status depends on the earlier fever status (represented

). A person’s reaction to aspirin is consistent, hence the

arc

4.5.2 Reasoning

Given evidence about a set of nodes, , from the ﬁrst time slice up to and includ-

ing the current time-slice

, we can perform belief updating on the full DBN, using

standard BN inference algorithms. This means obtaining new posterior distributions

for all the non-evidence nodes, including nodes in the

and later time-slices.

This updating into the future is called probabilistic projection.

However, this type of DBN gets very large, very quickly, especially if the interval

between time slices is short. To cope, in most cases the DBN is not extended far into

the future. Instead, a ﬁxed size, sliding “window” of time slices is maintained. As

the reasoning process moves forward with time, one older time slice is dropped off

the DBN, while another is added.

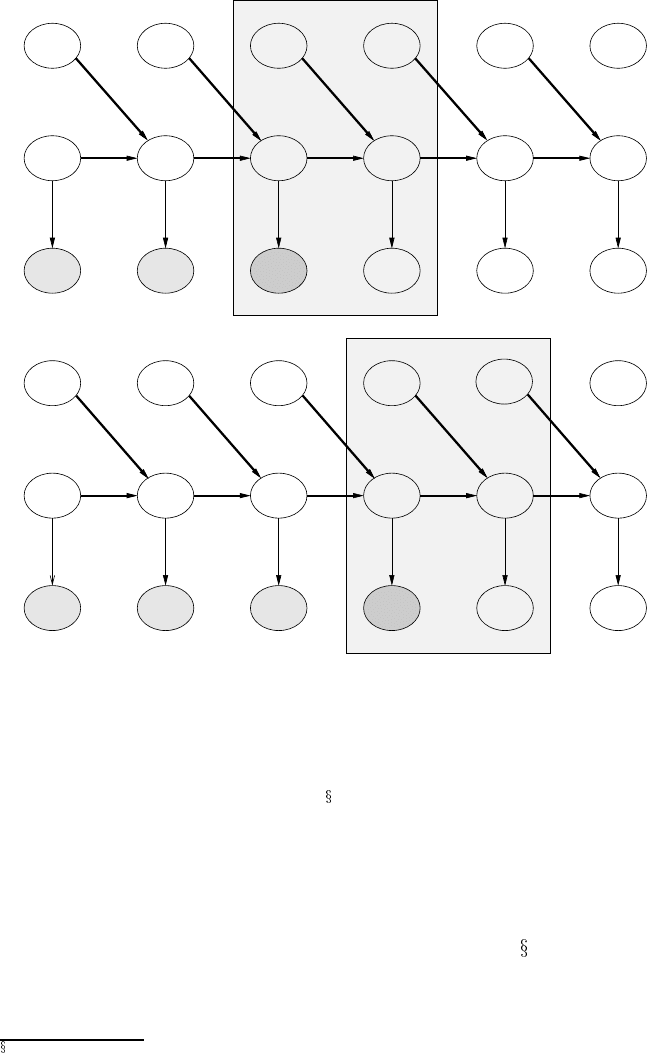
Figure 4.12 shows the progress of a simple two time-slice DBN. This structure

can be considered a generic DBN, consisting of state node

, its corresponding

observation node

, where evidence is added, and an action node that will

t+1t

t+1

current next

Obs

FIGURE 4.12

DBN maintained as a sliding “window” of two time-slices. (Shading indicates evi-

dence node.)

affect the state node at the next time step

This use of a ﬁxed window means that every time we move the window along, the

previous evidence received is no longer directly available. Instead, it is summarized

taking the current belief for (root) nodes, and making these distributions the new pri-

ors. The DBN updating process is given in Algorithm 4.5. Note that the steps of this

DBN updating algorithm are exactly those of a technique used in classical control

theory, called a Kalman Filter [138] (see Bibliographic notes in

4.8).

Note that this is a standard BN node representing a random variable, not a decision/action node from a

decision network.

ALGORITHM 4.5

DBN Updating Process

1. Sliding: Move window along.

2. Prediction:

(a) We already know

, the estimated probability distri-

bution over

(b) Calculate the predicted beliefs,

3. Rollup:

(a) Remove time-slice

(b) Use the predictions for the

slice as the new prior by setting to

4. Estimation:

(a) Add new observations

(b) Calculate

, the probability distribution over the current

state.

4.5.3 Inference algorithms for DBNs

Exact clustering algorithms can be applied to DBNs, particularly if the inference is

restricted to two time-slices

. Unfortunately, there normally is a cluster containing

all the nodes in a time slice with inter-slice connections, so the clusters become

unwieldy. The intuitive reason for this is that even if there are no intra-slice arcs

between two nodes, they often become correlated through common ancestors. A

version of the junction tree algorithm has been developed for DBNs [149]. This

method takes advantage of the DBN structure by creating a junction tree for each

time slice and performing updating for time slices up to and including the current

time-slice using inter-tree message passing. For probabilistic projection into future

time-slices, a sampling method is effective as there is no evidence yet for these future

time slices.

If the DBN clusters get too large, approximate algorithms using stochastic simu-

lation (described in

3.6) are usually suitable. As we discussed in 3.6.5, stochastic

simulation methods are more effective when the evidence is at the root nodes, while

the typical DBN structure involves the modeling of one or more state variables, each

of which is observed with a possibly noisy sensor. This structure is shown in Fig-

ure 4.12; we can see that in these models evidence is at the leaves.

This does not mean that the beliefs being maintained are exact, of course; since past evidence is being

summarized, the beliefs are inexact.

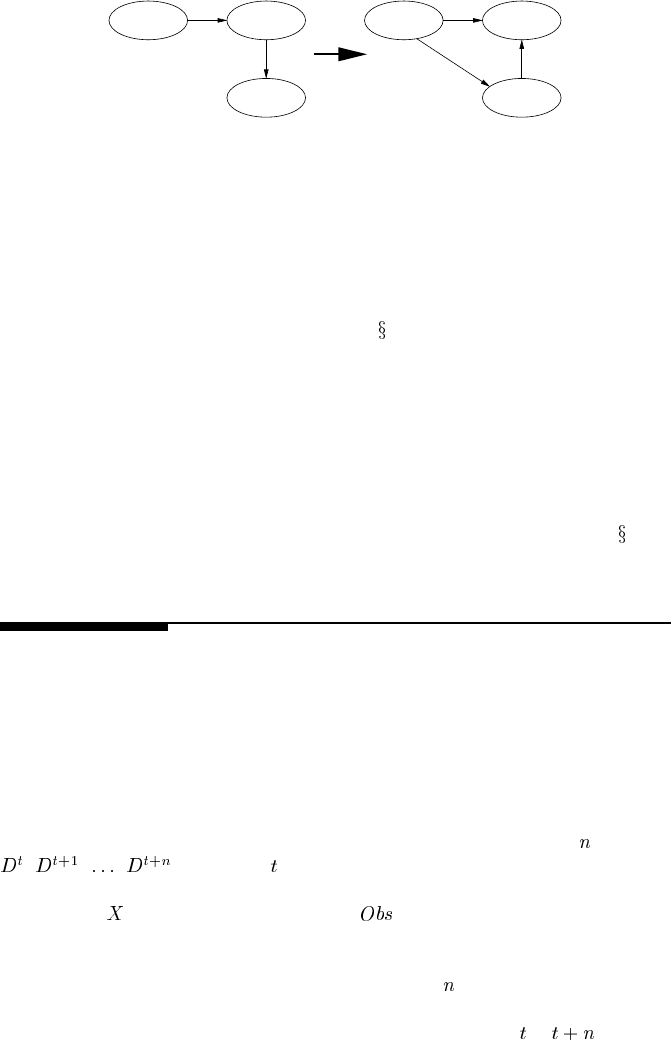
(a) (b)

State

t−1

State

Obs

State

t−1

State

Obs

FIGURE 4.13

(a) Original network; (b) new structure after arc reversal process.

One solution to this problem with stochastic simulation is to reverse the arcs to

evidence nodes, as proposed by Shachter [250], and then use the stochastic simula-

tion algorithms. This arc reversal method (see

6.3.1.1) ensures that the evidence is

at the root nodes, while maintaining the same overall joint probability distribution.

It requires the addition of arcs to maintain the conditional independencies. A simple

example is shown in Figure 4.13. The disadvantage is that we get a more complex

structure that does not model the causal relationships.

Many other approximate algorithms for DBN inference have been proposed, in-

cluding variations of stochastic simulation (e.g., [140]), ﬁltering methods (e.g., [198])

and ignoring weak dependencies in the stochastic process (e.g., [31, 133, 148]). Un-

fortunately, most of these are not implemented in BN software packages (see

B.4).

4.6 Dynamic decision networks

Just as Bayesian networks can be extended with a temporal dimension to give DBNs,

so can decision networks be extended to give dynamic decision networks (DDNs).

Not only do they represent explicitly how the world changes over time, but they

model general sequential decision making.

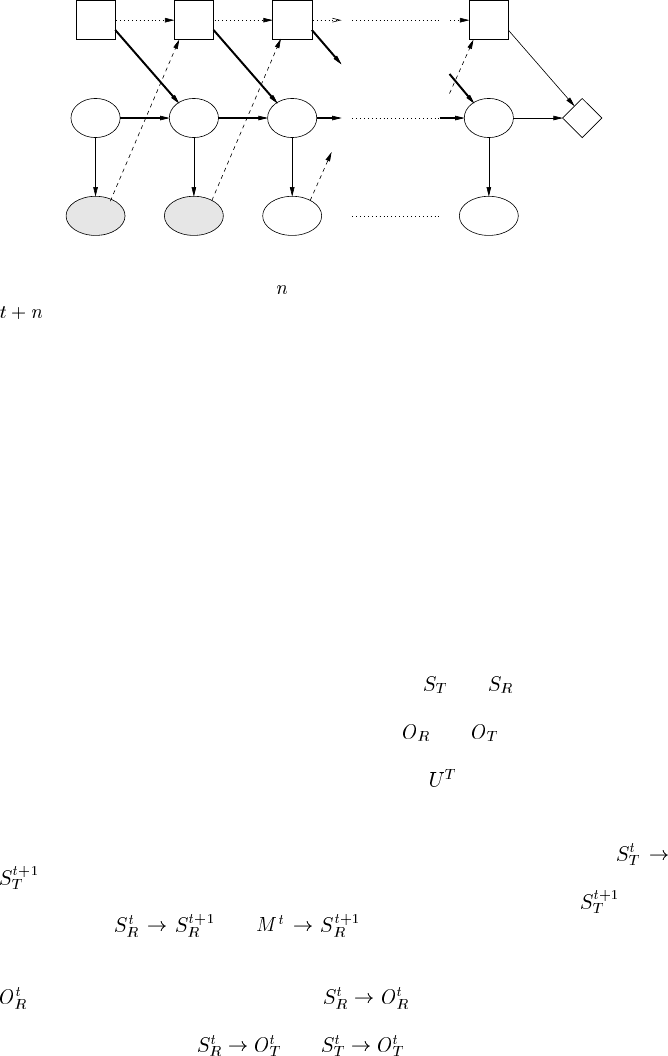
Figure 4.14 shows a generic DDN structure, for making a sequence of

decisions

, , , , from time into the future. The temporal sequencing of the

decision is represented by the precedence link (shown as a dotted line). The single

chance node

determines the utility, while is the observation node for which

evidence will be added before each subsequent decision; this sequencing is repre-

sented by the information link (shown as a dashed line). Note that in Figure 4.14 the

decision making will maximize the expected utility in

time steps. Another alter-

native would be to have a utility node at each time slice, in which case the decision

making will maximize the cumulative expected utility from time

to .

The DDN structure for the fever example is shown in Figure 4.15.

t+1

t+n

Obs ObsObsObs

t+n

t−1 t

t−1

t+1

FIGURE 4.14

A generic DDN for a sequence of

decisions, to maximize expected utility at time

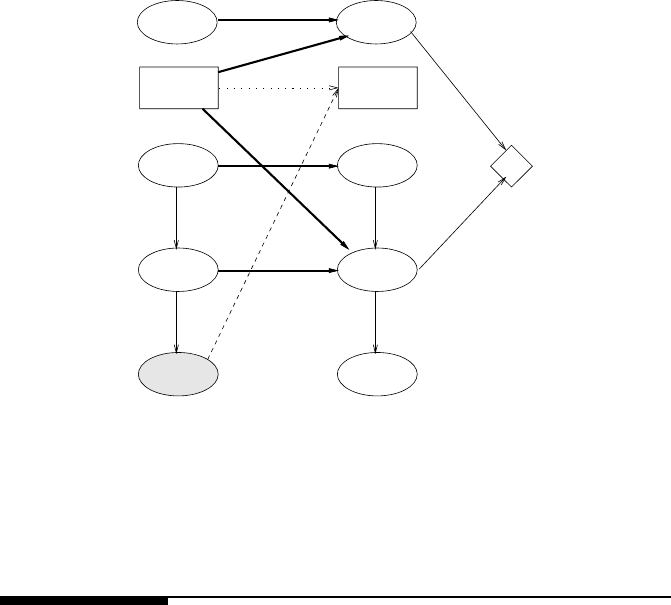
4.6.1 Mobile robot example

The robot’s task is to detect and track a moving object, using sonar and vision sensor

information, given a global map of the ofﬁce ﬂoor environment. The robot must also

continually reassess its own position (called localization) to avoid getting lost. At

any point in time, the robot can make observations of its position with respect to

nearby walls and corners and of the target’s position with respect to the robot.

This deceptively simple, yet interesting, problem of a mobile robot that does both

localization and tracking (a slightly simpliﬁed version of the one presented in [70])

can be modeled with a DDN as follows. The nodes

and represent the loca-

tions of the target and the robot, respectively. The decision node is M, representing

the robot’s movement actions options. The nodes

and represent the robot’s

observations of its own and the target’s location, respectively. The overall utility is

the weighted sum over time of the utility at each step,

, which is a measure of the

distance between the robot and its target.

The DDN using these nodes is shown in Figure 4.16. The temporal arcs

indicate that the target’s next position is related to its previous position; the

actual model of possible movement is given implicitly in the CPT for

.The

temporal arcs

and indicate that the robot’s own location

depends on its previous position and the movement action taken. Both observation

nodes have only intra-slice connections. The robot’s observation of own position

depends only on its actual position ( ), while its ability to observe the

position of the target will depend on both the target’s actual location plus its own

position (represented by

and ), as it has to be close enough for

its sensors to detect the target.

Flu

React

t t+1

React

t+1t

t+1

Flu

t t+1

t+1

Fever Fever

FIGURE 4.15

DDN structure for the fever example.

4.7 Summary

In order to make decisions, we must be able to take into account preferences between

different outcomes. Utility theory provides a way to represent and reason with pref-

erences. The combination of utility theory and probability theory gives a framework

for decision making, where a rational being should make choices that maximize her

or his expected utility. Extending Bayesian networks with decision nodes and utility

nodes gives us decision networks (also called inﬂuence diagrams). These include

an explicit representation of ordering between information and decisions, and de-

cisions and decisions, and allow us to make isolated or sequential decisions. By

adding a temporal dimension to Bayesian networks, we get dynamic Bayesian net-

works (DBNs), which allow us explicitly to model and reason about changes over

time. These in turn can be extended with utility and decision nodes, to give dynamic

decision networks (DDNs). DDNs run into complexity problems when used for gen-

eral planning, in which case special purpose planning representations and algorithms

may be more useful.