Конверський А. Є. Логіка (традиційна та сучасна)

Подождите немного. Документ загружается.

Книга друга. СУЧАСНА ЛОГІКА

471

К.Льюїс вважає, що наслідок (2) із Df 4 є джерелом

«парадоксів» матеріальної імплікації.

Якщо р p (q p р), то р ⊃ (q ⊃ р). Значить, коли «р» іс-

тинне, то будь-яке висловлювання матеріально поро-

джує «р». Але аналог зі строгою нестверджувальною ім-

плікацією не приймається:

р p (q p р).

Якщо ∼р p (р ⊃ q), то ∼р ⊃ (р ⊃ q). Отже, при хибності

«р» з нього випливає матеріально будь-яке «q». І знову

аналог зі строгою імплікацією не приймається:

∼р p (рp q).

Візьмемо наступну низку теорем:

а) ∼(р ⊃ q) p (р ⊃ ∼q) – аналогом є ∼(р ⊃ q) ⊃ (р ⊃ ∼q);

б) ∼(р ⊃ ∼q) p (р ⊃ q) – аналогом є ∼(р ⊃ ∼q) ⊃ (р ⊃ q).

Виходить, що коли ми маємо висловлювання «р» і

«q», то «р» повинно імплікувати матеріально істинність

«q», в протилежному випадку «р» буде імплікувати хиб-

ність «q».

Оскільки, якщо б «р ⊃ q» була прийнята за еквівалент

виразу «із р вивідним є q», то ні одна пара висловлювань

не могла б бути одночасно сумісною і незалежною. Тому

що відомо, коли «р» і «q» сумісні, то «р» не може імплі-

кувати хибність «q», а коли «q» незалежне від «р», то «р»

не може імплікувати істинність «q». Цей факт є основним

проти того, щоб ототожнювати змістовне логічне слідуван-

ня з матеріальною імплікацією. Для більш повного опису

змістовного логічного слідування К.Льюїс вводить ще дві

дефініції:

Df 6. р

q = ∼(р p ∼q).

Це визначення відношення сумісності: «р і q сумісні,

тоді і тільки тоді, коли не може бути такого, щоб із р

строго імплікувалася хибність q».

Df 7. ◊р = р

р = ∼(р p ∼р)

– «◊» – це модальний оператор «можливо». ◊р читається:

«р самосумісно», або «р не породжує свого заперечення»,

або «р можливо». Якщо ми введемо заперечення, то отри-

маємо низку похідних операторів:

∼◊ р – «р неможливе», або «хибно, що р можливе»;

А. Є. Конверський. ЛОГІКА

472

◊ ∼р – «можливо, що р хибне», або «р не необхідно

істинне»;

∼ ◊ ∼р – «неможливо, що р хибне», або «р необхідно

істинне».

К.Льюїс тлумачить так модальні оператори «можливо»,

«неможливо», «необхідно»:

 ◊р – розуміється як логічно можливе, як відсут-

ність самосуперечки, як логічно мислиме;

 ∼◊р – розуміється як логічна неможливість, як

логічно немислиме;

 ∼◊∼р – розуміється як логічна необхідність, як ло-

гічна немислимість того, щоб «р» було хибним.

Використовуючи модальні оператори К.Льюїс вводить

низку теорем, серед яких:

1) р p ◊р;

2) ∼◊∼р p р;

3) ∼◊∼р p ◊р.

Застосовуючи аксіоматику К.Льюса, теореми 1, 2 і пра-

вила доведення, побудуємо доведення теореми 3.

Візьмемо аксіому VI

1. [(p p q) ∧ (q p r)] p (p p r)

2. [(∼◊∼p p p) ∧ (p p ◊р)] p (∼◊∼р p ◊р) – за правилом

підстановки до 1 p/∼◊∼p, q/p, r/◊p

3. (∼◊∼р p р) ∧ (р p ◊р) – за принципом логічного до-

бутку

4. ∼◊∼р p ◊р – за правилом інференції.

До семи аксіом своєї системи К.Льюїс додає аксіому

VIII, яка іменується «постулат сумісності»:

VIII. ◊(pq) p ◊p.

За допомогою цієї аксіоми К.Льюїс виводить низку тео-

рем, серед яких вирази, що співзвучні з «парадоксами»

матеріальної імплікації, але тепер вони отримані в системі

строгої імплікації:

1. «Неможливе висловлюванння породжує будь-яке

висловлювання»

∼◊p p (p p q).

2. «Необхідно істинне висловлювання породжує будь-

яке висловлювання»

∼◊∼р p (q p p).

Книга друга. СУЧАСНА ЛОГІКА

473

К.Льюїс не важає ці формули за парадокси, оскільки вони

не суперечать змістовному тлумаченню логічного слідуван-

ня, як це відбувається з подібними виразами в системі ма-

теріальної імплікації.

В цілому концепція К.Льюїса є значимим внеском у

розвиток сучасної модальної логіки.

2. Концепція модальної логіки Я.Лукасевича

а) Тризначна система Я.Лукасевича

Ідею появи модальної логіки Я.Лукасевича спричинили

його дослідження модальної логіки Арістотеля, який у

своїх працях «Про витлумачення» та в «Першій аналіти-

ці» використовує модальні терміни: «необхідно», «можли-

во», «неможливо», «випадково».

Терміни «необхідно» і «можливо» беруться за основні.

Позначимо їх відповідно «М» і «L».

У творі «Про тлумачення» Арістотель стверджує, що

«можливість розуміється як відсутність необхід-

ності».

Я.Лукасевич фіксує цей факт у вигляді залежностей:

1. «Якщо можливо, що «р», то не необхідно «р».

Але з цієї залежності випливає, що необхідність утри-

мує в собі можливість.

2. «Якщо необхідно, що «р», то можливо, що «р».

Тоді за правилом гіпотетичного силогізму отримуємо із

2-го 1-ше.

3. «Якщо необхідно, що «р», то не необхідно, що «р».

Виходить нісенітниця. Пізніше, у «Першій аналітиці»,

Арістотель виправляє ситуацію за допомогою введення та-

кої еквівалентністі:

4. «Можливо, що «р», якщо і тільки якщо не необхід-

но, що не «р».

А відношення необхідності до можливості, про яке го-

ворить Арістотель в роботі «Про тлумачення», Я.Лукасевич

формулює у вигляді такої залежності:

5. «Необхідно, що «р», якщо і тільки якщо не можли-

во, що не «р».

Використовуючи символіку Я.Лукасевича, 4 і 5 залежніть

можна виразити таким способом:

А. Є. Конверський. ЛОГІКА

474

 QMpNLNp – читається: Mp – якщо і тільки якщо

– NLNp;

 QLpNMNp – читається: Lp – якщо і тільки якщо

– NMNp.

Я.Лукасевич вбачав основний недолік попередніх дослі-

джень у галузі модальних логік – це відсутність ефектив-

них логічних засобів для фіксації модальних понять. Та-

ким інструментом, на його думку, може стати логіка, яка

приписує одному висловлюванню більше ніж два значення.

Першою його пропозицією була тризначна пропозиційна

логіка.

Запропонована Я.Лукасевичем система складається

із немодальної і модальної частин.

Немодальна частина включає в себе:

1. Список пропозиційних змінних: p, q, r, ….

2. Список пропозиційних зв’язок: N, K, A, C, Q, (відпо-

відно: ¬, ∧, ∨, ⊃,∾).

3. Дефініцію формули.

4. Дефініцію пропозиційних зв’язок.

5. Дефініцію доказової формули.

До модальної частини відносяться:

1. Список модальних функторів: M, L, NM, D.

2. Дефініція формули.

3. Дефініція модальних функторів.

4. Дефініція доказової формули.

Кількість можливих значень, яке може мати довільне

висловлювання, дорівнює трьом (1, 0, ½).

 1 ставиться у відповідність оцінка «істинно»;

 0 – «хибно»;

 ½ – «невизначено».

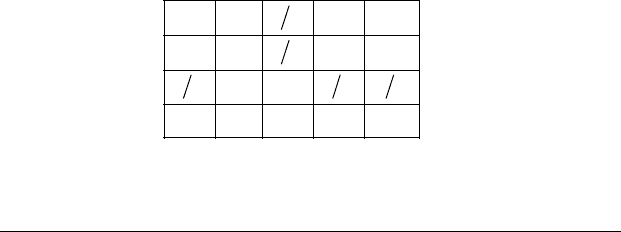
Пропозиційні зв’язки заперечення та імплікація зада-

ються табличним способом:

11110

21211121

002111

0211 NpC

Пропозиційні зв’язки кон’юнкції, диз’юнкції, еквівале-

нції задаються відповідними дефініціями.

Книга друга. СУЧАСНА ЛОГІКА

475

Розглянемо їх послідовно.

рAq = Df pCqCq

1. рАq = 1А1 = 1С1С1 = 1С1 = 1

2. рАq = 0А0 = 0С0С0 = 1С0 = 0

3. рАq = 1А0 = 1С0С0 = 0С0 = 1

4. рАq = 0А1 = 0С1С1 = 1С1 = 1

5. рАq = ½ А½ = ½ С½ С½ = 1С½ = ½

6. рАq = ½ А1 = ½ С1С1 = 1С1 = 1

7. рАq = 1А½ = 1С½ С½ = ½ С½ = 1

8. рАq = ½ А0 = ½ С0С0 = ½ С0 = ½

9. рАq = 0А½ = 0С½ С½ = 1С½ = ½.

pKq = Df N(NpANq)

1. pKq = 1K1 = N(N1AN1) = N(0A0) = N0 = 1

2. pKq = 1K0 = N(N1AN0) = N(0A1) = N1 = 0

3. pKq = 0K1 = N(N0AN1) = N(1A0) = N1 = 0

4. pKq =0K0 = N(N0AN0) = N(1A1) = N1 = 0

5. pKq = ½ K½ = N(N½ AN½) = N(½ A½) = N½ = ½

6. pKq = ½ K1 = N(N½ AN1) = N(½ AN0) = N½ = ½

7. pKq = 1K½ = N(N1AN) = N(0A½) = N½ = ½

8. pKq = 0K½ = N(N0AN½) = N(1A½) = N1 = 0

9. pKq = ½ K0 = N(N½ AN0) = N(½ A1) =N1 = 0.

pQq = Df pCqKqCp

1. pQq = 1Q1 = 1C1K1C1 = 1K1 = 1

2. pQq = 1Q0 = 1C0K0C1 = 0K1 = 0

3. pQq = 0Q1 = 0C1K1C0 = 1K0 = 0

4. pQq = 0Q0 = 0C0K0C0 = 1K1 = 1

5. pQq = ½ Q½ = ½ C½ K½ C½ = 1K1 = 1

6. pQq = ½ Q1 = ½ C1K1C½ = 1K½ = ½

7. pQq = 1Q½ = 1C½ K½ C1 = ½ K1= ½

8. pQq = ½ Q0 = ½ C0K0C½ = K1 = ½

9. pQq = 0Q½ = 0C½ K½ C0= 1K0 = 0.

Модальні функції в трьохзначній системі Я.Лукасевича

є функціями від трьох значень істинності (1, 0, ½).

Вихідною модальною функцією є можливість (М). Че-

рез можливість визначаються неможливість і необхідність.

Змістовна трактовка можливості передбачає зв’язок іс-

нування і можливого стану, дії, результату тощо. Іншими

А. Є. Конверський. ЛОГІКА

476

словами, існування чогось передбачає його можливість,

але не навпаки. Виходячи із цього, Я.Лукасевич тлумачить

істинністну функцію можливості в аспекті трьох істинніс-

тних оцінок таким способом:

1) р, q, r …. – це змінні висловлювань, в яких відбува-

ється констатація чогось;

2) Мр, Мq, Мr, … – це змінні висловлювання, в яких

висловлюється оцінка з тієї чи іншої точки зору стосо-

вно змісту висловлювання: «Можливо, що р», «Можли-

во, що q».

Тоді, якщо висловлювання «р» має оцінку «1» (підтве-

рджено факт існування), то висловлювання «Мр» теж ма-

тиме оцінку «1». Це означає, що якщо дещо існує, то во-

но можливе.

Якщо висловлювання «р» має оцінку «0» (факт існу-

вання не підтверджено), то висловлювання «Мр» має оці-

нку «0», і цим самим підкреслюється відсутність реалі-

зації якоїсь можливості.

За певних умов деякий факт може мати місце, а може й

ні. Ця ситуація фіксується висловлюванням, яке має оцін-

ку «½» («невизначено»). Модальне висловлювання, яке

утворене від нього, матиме оцінку «1», цим самим вказу-

ючи на здатність чогось реалізуватися.

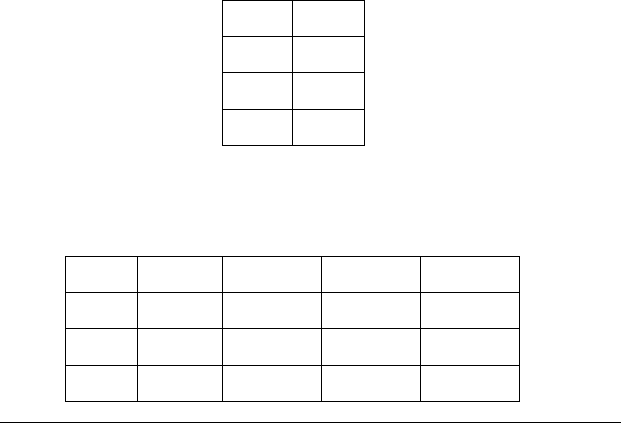
За допомогою таблиць зазначене можна відобразити так:

рМр

½ 1

Як уже зазначалося «М» є вихідною модальністю у Я.Лу-

касевича. Тому табличне визначення можливості є базовим

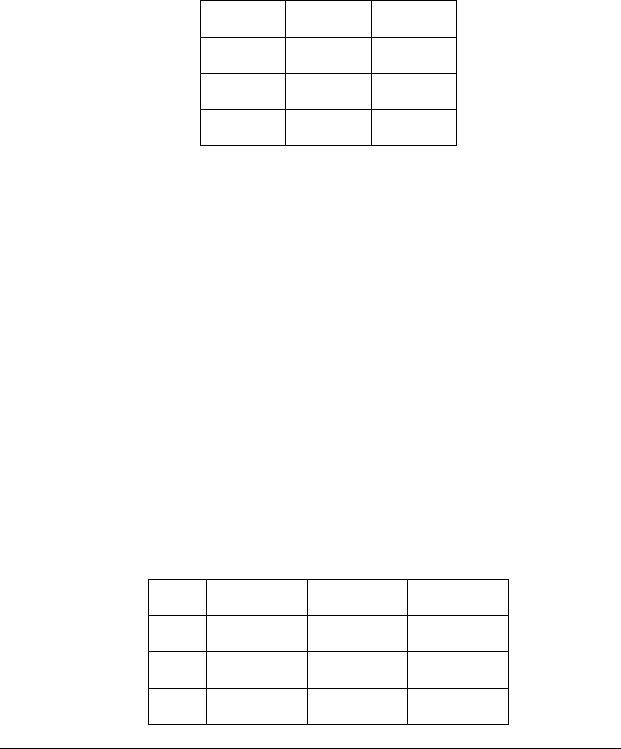
для визначеня інших модальностей.

рМрNMp MNp NMNp

11 0 0 1

½ 10 1 0

00 1 1 0

Книга друга. СУЧАСНА ЛОГІКА

477

Таким чином, ми будували таблиці для «неможливос-

ті» (NMp) і для «необхідності» (NMNp).

Я.Лукасевич задає модальну функцію «випадковість»

(D) за допомогою дефініції:

Dр = Df pQNp.

1. Dp = 1QN1 = 1Q0 = 0

2. Dp = 0QN0= 0Q1 = 0

3. Dp = ½ QN½ = ½ Q½ = 1.

У вигляді таблиці це можна представити так:

р Dр NDp

101

½ 10

001

NDp – це значення випадковості.

Прокоментуємо визначення випадковості.

З чисто змістовної точки зору, якщо у висловлюванні

«р» однозначно фіксується наявність якогось факту

або його відсутність, то це означає виключення будь-

якої випадковості. Іншими словами, якщо висловлюван-

ня «р» має оцінку «1» або «0», то модальне висловлю-

вання «Dр» матиме оцінку «0». А коли у висловлюванні

«р» фіксується рівноцінність як того, що може мати

місце, так і того, що не може мати місця (це відобра-

жається оцінкою «½»), то модальне висловлювання

«Dр» оцінюється «1».

У запропонованій Я.Лукасевичем системі вивідними

(доказовими) є тільки ті формули, які при будь-якій ком-

бінації значень приймають значення «1».

Візьмемо дві формули: pCMp і MpСр перевіримо їх на

доказовість.

рМррСМрМрСр

1111

½ 11½

00 1 1

А. Є. Конверський. ЛОГІКА

478

Отже, формула рСМр є доказовою і вона приймається в

системі Я.Лукасевича, а формула МрСр не є доказовою і

вона відкидається у цій системі.

б) Чотиризначна система Я.Лукасевича

У роботі «Арістотелівська силогістика з точки зору

сучасної формальної логіки» Я.Лукасевич розробляє сис-

тему модальної логіки, яку називає «Основна модальна

логіка».

До основної модальної логіки він відносить вісім за-

лежностей, які повинна обов’язково мати будь-яка сис-

тема, що претендує бути модальною:

1. QMpNLNp, тобто Mp – тоді і тільки тоді, якщо

NLNp (можливо, що «р» тоді і тільки тоді, якщо не не-

обхідно «не-р»);

2. QLpNMNp, тобто Lp – тоді і тільки тоді, якщо

NMNp (необхідно, що «р» тоді і тільки тоді, якщо не

можливо, що «не-р»);

3. CLpp, тобто, якщо Lp, то «р» (якщо необхідно, що

«р», то «р»);

4. CpMp, тобто, якщо «p», то Mp (якщо наявне (існує)

«р», то можливо, що «р»);

5. CMpp, тобто, якщо Mp, то «р» (якщо можливо, що

«р», то наявне (існує) «р»);

6. CpLp, тобто якщо «р», то Lp (якщо наявне (існує)

«р», то необхідно, що «р»);

7. Mp, тобто можливо, що «р»;

8. NLp, тобто не необхідно, що «р».

Посилаючись на дослідника творчості Арістотеля Алек-

сандра Афродизійського, Я.Лукасевич підкреслює, що іс-

нування (наявність) передбачає можливість, але не на-

впаки, а необхідність – існування (наявність), але не

навпаки. Ті залежності, де порушуються ці вимоги, по-

винні бути відкинуті.

Отже, формули 5 – 8 відкидаються в будь-якій системі.

Чотиризначна модальна логіка Я.Лукасевича включає в се-

бе немодальну частину і модальну. Немодальну частину скла-

дає чотирьохзначна логіка Я.Лукасевича, яка розглянута вище.

Модальну частину Я.Лукасевич задає у вигляді двох

альтернатив. У залежності від того, чи береться за

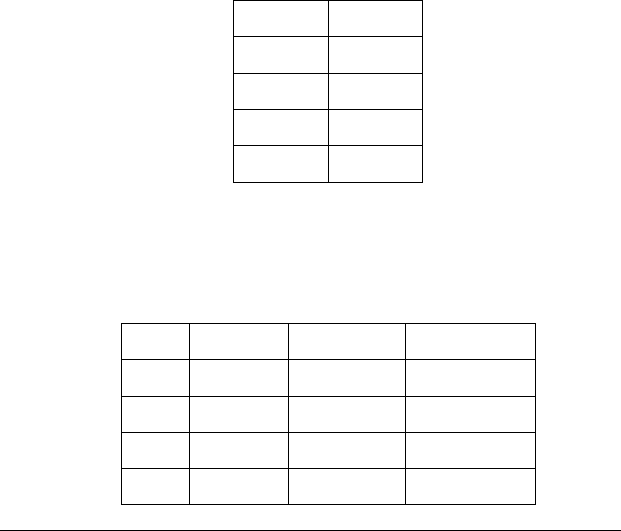
Книга друга. СУЧАСНА ЛОГІКА

479

вихідний функтор можливість (М), чи необхідність (L)

приймаються відповідні основні принципи модальної ло-

гіки:

І. СрМр, СМрр, Мр;

ІІ. СLрp, СрLр, NLp.

Характерною особливістю модальної логіки Я.Лукасеви-

ча є те, що тут модальності є функціями істинності.

Дамо визначення модальних функцій.

Визначимо можливість (М) на підставі рівності і

таблиці:

М (а,b) = (a, Cbb)

1. М (1,1) = (1,С11) = (1,1) = 1

2. М (1,0) = (1,С00) = (1,1) = 1

3. М (0,1) = (0,С11) = (0,1) = 3

4. М (0,0) = (0,С00) = (0,1) = 3.

У табличному варіанті можливість (М) має такий

вигляд:

рМр

Оскільки функтор М є вихідним, то через нього визна-

чається функтор L:

Lp = Df NMNp.

Дамо табличне визначення Lp:

p Np MNp NMNp

14 3 2

23 3 2

32 1 4

41 1 4

А. Є. Конверський. ЛОГІКА

480

У даній системі доказовою є формула, яка при будь-

яких підстановках значень приймає значення «1».

За допомогою введених визначень модальних функторів

спробуємо верифікувати декілька формул:

I) CLpp; II) CpMp; III) CМpp; IV) CpLp.

І) 1. CLpp = CL11 = C21 = 1

2. CLpp = CL22 = C22 = 1

3. CLpp = CL33 = C43 = 1

4. CLpp = CL44 = C44 = 1

II) 1. CpMp = C1M1 = C11 = 1

2. CpMp = C2M2 = C21 = 1

3. CpMp = C3M3 = C33 = 1

4. CpMp = C4M4 = C43 = 1

III) 1. CMpp = CM11 = C11 = 1

2. CMpp = CM22 = C12 = 2

3. CMpp = CM33 = C33 =1

4. CMpp = CM = 44 = C34 = 2

IV) 1. CpLp = C1L1 = C12 = 2

2. CpLp = C2L2 = C22 = 1

3. CpLp = C3L3 = C24 = 3

4. CpLp = C4L4 = C44 = 1.

Таким чином, формули I, II є доказовими, а III, IV –

ні, а це означає, що, за термінологією Я.Лукасевича, вони

повинні бути відкинуті.

Окрім функтора (М) для модальності «можли-

вість» Я.Лукасевич вводить ще один функтор (W). Позна-

чення для цього функтора виглядає як перевернута «М».

Визначає він цей функтор за допомогою рів-

ності:

W (a,b) = (Caa,b).

1. W (a,b) = (C11,1) = (1,1) = 1

2. W (1,0) = (C11,0) = (1,0) = 2

3. W (0,1) = (C00,1) = (1,1) = 1

4. W (0,0) = (C00,0) = (1,0) = 2.