Конверський А. Є. Логіка (традиційна та сучасна)

Подождите немного. Документ загружается.

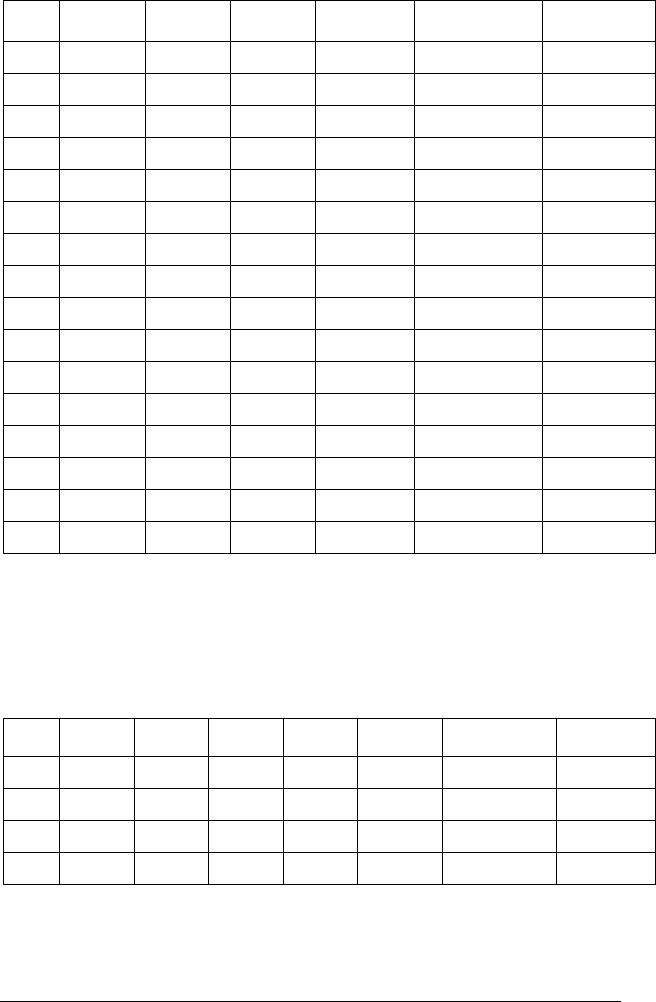
Книга друга. СУЧАСНА ЛОГІКА

451

№

qp ⊃q (p ⊃q) ∨ p (p ⊃q) ∨ p

1 1,1 1,1 0,0 0,0 1,1 1

2 1,1 1,0 0,1 0,1 1,1 1

3 1,1 0,1 1,0 1,0 1,1 1

4 1,1 0,0 1,1 1,1 1,1 1

5 1,0 1,1 0,0 0,1 1,1 1

6 1,0 1,0 0,1 0,1 1,1 1

7 1,0 0,1 1,0 1,1 1,1 1

8 1,0 0,0 1,1 1,1 1,1 1

9 0,1 1,1 0,0 1,0 1,1 1

10 0,1 1,0 0,1 1,1 1,1 1

11 0,1 0,1 1,0 1,0 1,1 1

12 0,1 0,0 1,1 1,1 1,1 1

13 0,0 1,1 0,0 1,1 1,1 1

14 0,0 1,0 0,1 1,1 1,1 1

15 0,0 0,1 1,0 1,1 1,1 1

16 0,0 0,0 1,1 1,1 1,1 1

Отже, даний вираз є доказуваним у чотиризначній ло-

гіці.

Перевіримо, чи будуть тавтологіями в чотиризначній

логіці закон виключеного третього і закон протиріччя:

(А∨



А) та  (А∧



А).

№А



АА ∨



АА ∨



АА ∧



 (А ∧А)  (А∧А)

1 1,1 0,0 1,1 1 0,0 1,1 1

2 1,0 0,1 1,1 1 0,0 1,1 1

3 0,1 1,0 1,1 1 0,0 1,1 1

4 0,0 1,1 1,1 1 0,0 1,1 1

Виходить, що закони виключеного третього і проти-

річчя залишаються тавтологіями і в чотиризначній

логіці.

А. Є. Конверський. ЛОГІКА

452

Це означає, що багатозначна логіка не завжди від-

кидає закони класичної логіки, тому більш конкрет-

ним буде все ж таки визначення багатозначної логіки

як такої, що визнає за висловлюванням більш ніж дві

оцінки.

Критика законів виключеного третього та протиріччя є

лише зовнішнім виявом тих процесів, які визначають від-

ношення між класичною та некласичною логікою. І це по-

трібно мати на увазі, даючи дефініцію класичної логіки.

Прокоментуємо дане положення.

Враховуючи факт існування класичної та некласич-

ної логіки, закон виключеного третього матиме три рі-

зні за формою дефініції:

а) «Будь-яке висловлювання або істинне, або хибне».

б) «Будь-якому висловлюванню або притаманне деяке

значення істинності, або ні».

в)

.AA∨

У наведених дефініціях закону виключеного третього

визначальними є характеристики диз’юнкції та заперечен-

ня. В усіх цих дефініціях диз’юнкція та запереченння ви-

ступають в узагальнюючому вигляді. Це означає, що для

одних визначень А ∧



А залишається законом (чотирьох-

значна логіка Я.Лукасевича), а для інших – ні (тризначна

логіка Я.Луксевича). Якщо ми приймемо, що тавтологією

є висловлювання, яке завжди приймає одне з двох значень

«1» або «½», то А ∧



А виявиться тавтологією:

А ∨



А = 1 ∨1 = 1∨ 0 = 1

А ∨



А = 0∨0 = 0 ∨ 1 = 1

А ∨



А = ½ ∨½ = ½ ∨ ½ = ½.

Третя дефініція закону виключеного третього А∨А (як

і закону протиріччя  (А∧



А) є приблизним позначенням

цього закону (тобто цей закон не можна зводити до відпо-

відної тотожньо-істинної формули, це лише певна експлі-

кація цього закону). І коли в підручниках з логіки в роз-

ділі «Закони логіки висловлювань» приводять закони

тотожності, виключеного третього, протиріччя як відпові-

дні тавтології (А ⊃ А, А ∨



А,  (А ∧



А)), то це не зовсім

коректно.

Особливо це відчутно, коли задається інтерпретація

диз’юнкції та заперечення в багатозначній логіці, при

Книга друга. СУЧАСНА ЛОГІКА

453

цьому вираз А ∨



А є законом (наприклад, в чотиризначній

логіці), то формула А ∨



А не буде законом виключеногo

третього у власному розумінні.

Виходячи з цього, завжди треба підходити прискіпливо

до тези: «закон виключеного третього в даній системі

не діє».

Якщо взяти чотиризначну логіку Я.Лукасевича, то

заява, що «кожне висловлювання або істинне, або хиб-

не» буде некоректною. Тут прийнятним є твердження:

«Будь-яке висловлювання має значення «1», або «2», або

«3», або «0». В іншому формулюванні: «Будь-яке вислов-

лювання або має значення істинності, або не має його

(має якесь інше з чотирьох можливих)».

Це ж саме стосується і закону протиріччя, але тут із

трьох можливих дефініцій перша зберігає силу і в багато-

значній логіці:

1. «Не може бути, щоб висловлювання було істинним

і одночасно хибним».

2. «Не може бути, щоб висловлювання мало і одноча-

сно не мало хоча б одне значення із числа можливих».

3. (А ∧



А).

Такі основні риси багатозначної логіки Я. Лукасевича.

2. Багатозначна логіка Брауера — Гейтінга

Як у розвитку будь-якої науки, так і у розвитку логіки

визначальними є два види причин:

а) внутрішні і

б) зовнішні.

Для логіки внутрішніми стимулами розвитку є роз-

робка та вдосконалення її апарату, а зовнішніми – ті

процеси в науковому пізнанні, для аналізу яких потріб-

ні засоби логіки.

Якщо для формування багатозначної логіки Я.Лукасе-

вича таким зовнішнім поштовхом був аналіз модальних

висловлювань, то для багатозначної логіки Брауера –

Гейтінга – потреба обгрунтування математики на

базі принципів інтуїціонізму.

Брауер виходить із положення: «Якщо закон виключе-

ного третього діє в кінцевій математичній системі, то

А. Є. Конверський. ЛОГІКА

454

в системі з нескінченними величинами він втрачає свою

абсолютність».

Гейтінг вводить таке табличне визначення для запере-

чення (N) та імплікації (С):

021

Nxx

10121

1110

21011

2101C

У формі рівностей Гейтінг так задає імплікацію:

1) С х,у = 1, якщо х

≤

у.

а) С х,у = С 0,1 = 1

б) С х,у = С 0, ½ = 1

в) С х,у = С ½,1 = 1

г) С х,у = С 0,0 = 1

д) С х,у = С 1,1 = 1

е) С х,у = С ½, ½ = 1

2) С х,у = у, якщо х > у.

а) С х,у = С 1,0 = 0

б) С х, у = С 1, ½ = ½

в) С х, у = С ½, 0 = 0

Якщо скласти результати двох рівностей, то отримаємо

наведену вище таблицю істинності для імплікації.

Порівняємо імплікацію тризначної логіки

Я.Лукасевича і Б.Гейтінга:

Я.Лукасевич: С х, у = С ½, 0 = 1 – ½ + 0 = ½

С х, у = С 1, ½ = 1 – 1 + ½ = ½.

Б.Гейтінг: С х, у = С ½, 0 = 0

С х, у = 1, ½ = ½.

Отже, повної подібності немає.

Кон’юнкцію і диз’юнкцію Б.Гейтінг визнaчає відповідно

за рівностями:

а) К х, у = min (х, у)

б) А х, у = max (х, у).

Книга друга. СУЧАСНА ЛОГІКА

455

а) б)

0000

0212121

02111

0211∧

02100

2121121

1111

0211∨

За допомогою таблиць істинності перевіримо, чи є тав-

тологіями вирази: CNNxx та AxNx:

1. CNNxx = CNN½½ = CN 0 ½ = C1½ = ½

2. AxNx = A½ N½= A½ 0 = ½.

Отже, закон подвійного заперечення і виключеного

третього в системі Брауера–Гейтінга не є доказовим.

В той час як вирази CxNNx і AAxNxNNx є тавтоло-

гіями:

1. CxNNx = C½ NN½ = C½ N0 = C ½1 = 1

2. CxNNx = C0 NN0 = C 00 = 1

3. CxNNx = C1 NN1 = C11 = 1.

Розглянемо вираз AAxNxNNx:

1. AAxNxNNx = AA1 N1 NN1 = AA101 = A11 = 1

2. AAxNxNNx = AA00 N0 NN0 = AA 010 = A01 = 1

3. AAxNxNNx = AA½ N½ NN½ = AAN½ N0 = A½1 = 1.

Даний вираз є своєрідним узагальненням закону ви-

ключеного третього: (р∨р) ∨р (враховуючи те, що в ло-

гіці Гейтінга подвійне заперечення не дорівнює ствер-

дженню). Все це свідчить про те, що багатозначна

логіка Гейтінга є доповненням, узагальненням двозна-

чної логіки.

Для доведення формул у даній системі будуються таб-

лиці істинності. Оскільки дана логіка тризначна, то таб-

лиця істинності будується за формулою «3

ⁿ

».

Візьмемо два вирази і побудуємо відповідні їм таблиці

істинності.

а) (p ⊃q) ∨ q;

б) p ⊃ (p ⊃ q).

А. Є. Конверський. ЛОГІКА

456

а)

№

qp ⊃q (p ⊃q) ∨ q

1110 0 1

21 ½ 00 ½

31 0 1 1 1

4 ½ 10 0 1

5 ½½00 ½

6 ½ 01 1 1

70 1 0 1 1

80 ½ 01 1

9001 1 1

б)

№ pq

pP ⊃ q p ⊃ (p ⊃ q)

11 1 0 1 1

21 ½ 0 ½ 1

31 0 0 0 1

4 ½ 10 1 1

5 ½½01 1

6 ½ 00 0 1

70 1 1 1 1

80 ½ 11 1

90 0 1 1 1

3. Багатозначна логіка Е.Поста

Як уже зазначалося, незалежно і майже одночасно з

Я.Лукасевичем почав розробляти систему багатозначної

логіки Е.Пост.

Він виходить із того, що висловлювання може мати не

декілька фіксованих значень, а відповідну множину «n»

(1, 2, 3, … n). Причому ці значення можуть бути різної

природи (а не тільки {істина … хиба}). Це можуть бу-

ти оцінки: {добро … зло}; {включено … виключено};

Книга друга. СУЧАСНА ЛОГІКА

457

{прекрасне ... потворне} тощо. Головне тут – логічні

відношення, у які вступають аргументи (висловлювання).

При побудові своєї системи Е.Пост вводить два запе-

речення.

Перше заперечення він називає «циклічним» поетап-

ним, а друге заперечення збігається із запереченням

Я.Лукасевича.

Перше заперечення позначимо  х, а

друге – ∼х.

Дамо табличне визначення цих заперечень:

−

......

−

......

У формі рівностей Е.Пост ще так визначав заперечення.

Перше заперечення (циклічне) визначається двома рів-

ностями:

1.  х =  х  + 1 при  х ≤ n — 1

2.  n =1.

Друге заперечення визначається однією рівністю:

∼ x = n —  x  + 1.

Прокоментуємо дані дефініції заперечення.

Візьмемо циклічне заперечення (1). Припустимо, що

наша система багатозначної логіки (у варіанті Поста) має 6

значень для одного висловлювання: 1, 2, 3, 4, 5, 6 (тобто

«6 = n», а «5 = n-1»).

Маємо висловлювання р, яке «пробігає» по множині да-

них значень. Знайдемо його значення впродовж усієї шка-

ли (від 1 до 6).

1.  р = 1+1 = 2

2.  р = 2+1 = 3

3.  р = 3+1 = 4

4.  р = 4+1 = 5

А. Є. Конверський. ЛОГІКА

458

5.  р = 5+1 = 6 (n)

6.  р = 6+1 = 1 (х = 1).

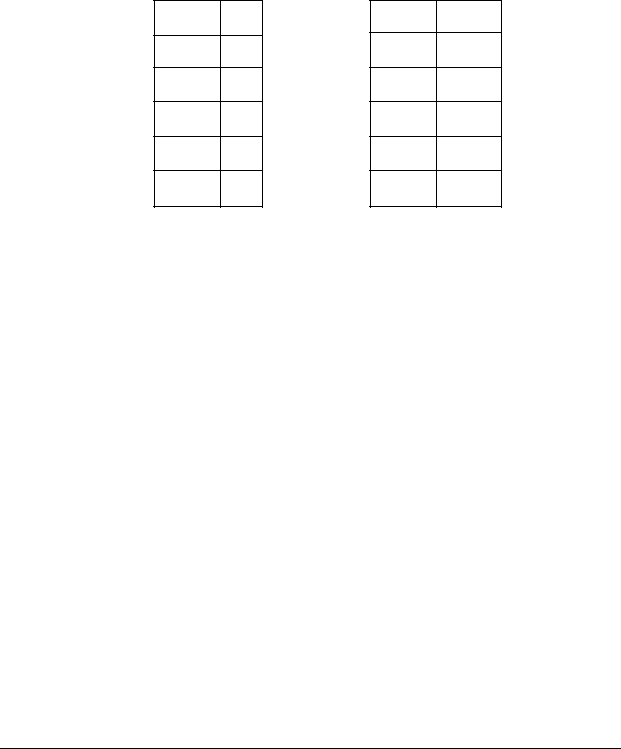
У табличному варіанті ця зв’язка матиме вигляд:

р  р

Тепер розглянемо другий варіант запереченя (∼х)

Е.Поста. Знову припустимо, що в нашій системі 6 значень

(1, 2, 3, 4, 5, 6) для довільного висловлювання.

1. ∼р = 6 — 1 + 1 = 6 при n = 6

2. ∼р = 6 — 2 + 1 = 5

3. ∼р = 6 — 3 + 1 = 4

4. ∼р = 6 — 5 + 1 = 3

5. ∼р = 6 — 5 + 1 = 2

6. ∼р = 6 — 6 + 1 = 1.

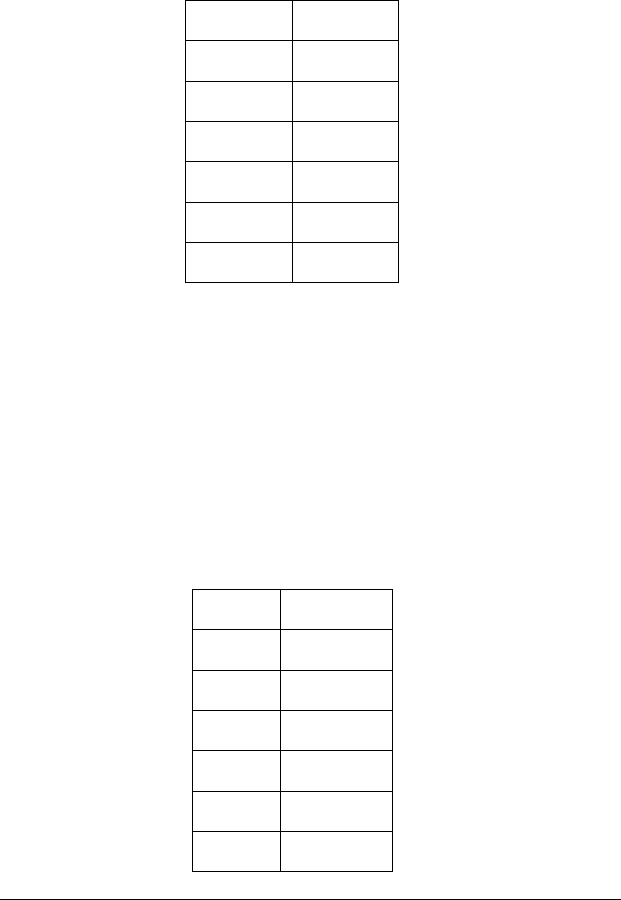
Табличний варіант для (∼х):

р ∼р

Книга друга. СУЧАСНА ЛОГІКА

459

Диз’юнкція і кон’юнкція визначаються відповідними

рівностями:

а) А xy = min (x,y)

б) К ху = max (x,y).

Тут необхідно мати на увазі, що в системі Е.Поста

більш стверджувальним (враховуючи те, що ми маємо

справу не з двозначною логікою, то за терміном «ствер-

джувальне» не треба розуміти «більш істинне») є те запе-

рчення, яке ближче по порядку до вихідного.

Наприклад, в системі із 6 значень (1, 2, 3, 4, 5, 6) більш

стверджувальним буде «2», а не «3».

Розглянемо наведені приклади диз’юнкції та кон’юн-

кції:

1. Аху = min (1, 2) = 1

2. Аху = min (2, 3) = 2

3. Аху = min (3, 4) = 3

4. Аху = min (4, 5) = 4

5. Аху = min (5, 6) = 5.

Табличний варіант:

∨ 123456

1111111

2122222

3123333

4123444

5123455

6123456

Визначимо таким самим способом кон’юнкцію:

1. Кху = max (1,2) = 2

2. Кху = max (2,3) = 3

3. Кху = max (3,4) = 4

4. Кху = max (4,5) = 5

5. Кху = max (5,6) = 5.

Табличне визначення:

А. Є. Конверський. ЛОГІКА

460

∧ 123456

1123456

2226456

3333456

4444456

5555556

6666666

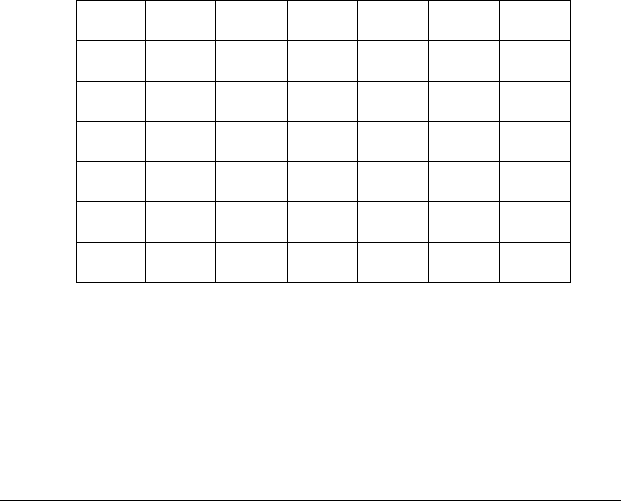
Використовуючи введені Е.Постом обидва варіанти за-

перечення, диз’юнкцію та кон’юнкцію, визначимо вирази:

p ∨р,  (р ∧р).

Припустимо, що в нашій системі n = 6:

р  р ∼ рр ∨  р  (р∨ р) р ∧ ∼р ∼ (р ∧ ∼р)

12 6 1 2 6 1

23 5 2 3 5 2

34 4 3 4 4 3

45 3 4 5 4 3

56 2 5 6 5 2

61 1 1 1 6 1

4. Тризначна логіка Д. Бочвара

Відомий математик, логік Д.Бочвар в 1938 р. запро-

понував тризначну систему логіки, яка розповсюджується

не лише на істинні та хибні висловлювання, а й на висло-

влювання, які не мають смислу.

Відповідно до цього він вводить три значення:

«1» – істинно;

«2» – хибно;

«3» – беззмістовно.