Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций

Подождите немного. Документ загружается.

диффузией факте, что в ряде случаев вычисляемая из скорости распро-

странения пламени энергия активации оказывается меньше энергии ак-

тивации реакции медленного горения. На основании этих данных Вольф-

гард и Гейдон приходят к заключению, что в случае быстрых реакций

горения либо нужно отказаться от применения закона Аррениуса, либо

под входящей в этот закон энергией активации понимать величину,

имеющую иной смысл, чем тот, какой она имеет в медленных реакциях

Основания для такого заключения нам представляются, однако, весьма

шаткими и вопрос в целом недостаточно изученным для того, чтобы были

возможны столь далеко идущие выводы. Фактическое положение дела

скорее отвечает обратной картине, так как проверка на опыте основываю-

щихся на законе Аррениуса теоретических выводов, относящихся к

распространению пламен, говорит о достаточно строгом выполнении

этого закона.

Пределы распространения пламени

Как мы видели, при изменении состава горючей смеси изменяется и

скорость распространения пламени. При некотором оптимальном составе

смеси скорость горения имеет максимальное значение и уменьшается

как в сторону бедной, так и в сторону богатой смеси. Начиная с некоторого

предельного состава, пламя не распространяется; иными словами, в

таких смесях и

= 0. Этот предельный состав, выражаемый содержанием

горючего в смеси или соответствующей величиной а, характеризует

концентрационные пределы распространения пламени. Опыт показыва-

ет, что при переходе за концентрационный предел распространение пла-

мени прекращается при некотором конечном значении и

Существование пределов распространения пламени естественно свя-

зать с явлением пределов воспламенения, перенося представления о вос-

пламенении газа в статических условиях на воспламенение свежей смеси

в условиях распространяющегося фронта горения. Из этого, однако,

не следует, что температура (Т

) и давление воспламенения (р

) смеси

данного состава в условиях пламени и в статических условиях будут

одними и теми же. Дело здесь заключается в том, что если в обоих случаях

условие воспламенения можно выразить равенством скорости разветвления

и скорости обрыва цепей (справедливом также и в случае теплового вос-

пламенения) [1656], то время приближения смеси к состоянию, отвечаю-

щему этому условию, вообще говоря, будет в каждом случае иным. При-

чиной этого может быть, например, различие теплопередачи при проте-

кании реакции в статических условиях и в условиях пламени. В резуль-

тате состояние смеси в момент воспламенения, характеризующееся

величинами Т

и р

, в обоих случаях будет различным, т. е. различными

будут соответственно Т

и р

Из определения условия воспламенения как равенства скоростей

разветвления и обрыва цепей следует, что все факторы, влияющие на про-

текание этих процессов, будут в той или иной степени влиять на Т

и р

. Не останавливаясь на анализе различных факторов, отметим, толь-

ко, что тепловой фактор (тепловые потери), по-видимому, играет здесь

доминирующую роль (см. например, [116, 117, 1215, 1349, 1524, 1568,

1569]).

С этой точки зрения Гейдон и Вольфгард [827] считают большим шагом вперед раз-

работанную Бехертом [459] формально-математическую теорию распространения

пламени, в которой энергия активации фигурирует как некоторый параметр, значе-

ние которого выбирается таким, чтобы вычисляемая при его помощи скорость пламе-

ни была ближе к измеренной величине.

Одна из первых теорий пределов распространения пламени, в основе

которой лежит представление о доминирующей роли тепловых потерь,

принадлежит Зельдовичу [116, 117], который показал, что потери тепла

приводят к уменьшению скорости пламени. На основании тепловой

теории распространения пламени Зельдовича и Франк-Каменецкого

.(см. выше) Зельдович получает равенство (см. также [365, стр. 312—316])

= ехр (50.21)

где £ =

(UQ/UQ)

(и

— скорость пламени в отсутствие тепловых потерь,

2%Ф Е 1

и'о— при наличии потерь) и а = , — (и — коэффициент темпе-

С/рро til pi

ратуропроводности, равный

% —

УС

, Я — средний коэффициент тепло-

проводности, Ф — потери тепла за 1 сек путем теплоотдачи во внешнее

пространство, отнесенные к 1 см

зоны горения, С

— теплоемкость,

Ро — плотность исходной смеси при темцературе Т

, Е — энергия

активации лимитирующего процесса, Т

— максимальная ^температура

пламени в отсутствие тепловых потерь и Т

— при наличии потерь).

Нетрудно показать, что предыдущее равенство ^имеет вещественное

решение только при определенных значениях параметра а, а именно

при значениях, разных или меньших некоторого критического значения

Якрит

• При этом критическом значении получается единственное

действительное решение £ = е, из которого следует

= Щ/ V7. (50.22)

Это значение величины щ представляет собой минимальное значение

скорости пламени, отвечающее пределам распространения. Таким образом,

в соответствии с опытом минимальное значение величины щ отлично от

нуля.

Зельдовичем также было показано [117, 122], что при определенных

условиях главную роль» играют потери тепла посредством излучения.

Линнетт и Симпсон [1161] (см. также [1172]) находят, что существен-

ное влияние на пределы распространения пламени оказывает конвекция.

О пределах распространения пламени далее см. [223, глава 5, § 12].

Вблизи пределов распространения пламени наблюдаются явления,

свидетельствующие о неустойчивости процесса горения, прогрессирую-

щей по мере приближения к пределам. Эти явления, выражающиеся в

зависимости концентрационных пределов распространения пламени в

вертикальных трубах от направления распространения (сверху вниз

пламена распространяются в более узких пределах концентрации, чем

снизу вверх, т. е. труднее [1666]), в искажениях или в неустойчивости

сплошного плоского фронта пламени [162], наиболее резко выражены

в смесях газов, сильно различающихся по молекулярному весу. Количест-

венное рассмотрение вопроса о неустойчивости пламен вблизи пределов

распространения принадлежит Лейзеру [1135]. См. также [1524].

§ 51. ДЕТОНАЦИЯ

В заключение этой главы кратко рассмотрим детонационное распро-

странение пламени в газовых смесях. Явление детонации газов, открытое

в 1881 г. Малларом и Ле-Шателье [1195] и независимо от них Вертело

[483], имеет огромное практическое значение. Поскольку одно из прояв-

лений детонации связано с ее разрушительным действием, то вполне

естественно, что именно катастрофические взрывы пылевоздушных смесей

в угольных шахтах послужили тем стимулом, который возбудил интерес

к явлениям распространения пламени и привел к открытию детонации

и в дальнейшем к ее всестороннему изучению. К той же категории явле-

ний относится детонация газовых и пылевидных смесей в условиях раз-

личных производств, как и детонация в двигателе внутреннего сгорания,

приводящая к быстрому износу и разрушению двигателя. Не входя, в

рассмотрение явления детонации с точки зрения практики, здесь коснемся

только тех его сторон, которые в той или иной мере связаны с химией

и кинетикой процессов горения.

Детонация возникает под действием ударных волн, в частности, в ре-

зультате самоускорения пламени (при распространении горения в трубах).

Вследствие самоускорения пламени возникает волна сжатия (ударная

волна), в которой благодаря высоким температуре и давлению происхо-

дит самовоспламенение смеси [118, 119., 123, 390].

Таким образом, возникающая при детонации ударная волна сопровож-

дается волной горения; обе волны, в совокупности образующие детона-

ционную волну, распространяются в газе с некоторой скоростью (скорость

детонации), которая значительно превосходит нормальную скорость пла-

мени и обычно составляет 2—5 км/сек.

В основе теории детонации, развитой Чепменом [626], Михельсоном

1239] и Жуге [1029] (см. также 460]), лежит гидродинамическая теория

ударных волн в химически инертном газе, ранее разработанная Риманом

(I860 г.), Ренкином (1870 г.) и Гюгоньо (1887, 1889 гг.). Исходя из гидро-

динамического уравнения непрерывности газового потока (закон сохра-

нения массы),

WoPo

= мр (51.1)

или

Uolvo

= u/v

где и — скорость; р — плотность и v — удельный объем газа (v = 1/р,

индекс «0» относится к холодному газу, находящемуся при начальной тем-

пературе Т

), и закона сохранения количества движения

1 и

— + = — +

(51.2)

{р — давление), путем простых преобразований находим (здесь и и и

—

••скорости газа в системе координат, движущейся вместе с ударной

волной):

р —

Ро

тт

1 Г р

— Ро

и = v

г?

— г?

vo —

Определяя скорость ударной волны кдк скорость движения фронта

волны по отношению к холодному газу и отмечая штрихом величины, отно-

сящиеся к газу во фронте волны, для скорости распространения ударных

волн будем иметь:

Соответственно скорость горячего газа относительно холодного

w = — Y(p' — p,)(vo — v'). (51.4)

(.Р' -

ро)

Ар

(vo —

v') Ay

Заметим, что при р' — р

и v

— v' << v

, когда \

~ '

ВВИД

У адиабатичности процесса при бесконечно малых измене-

ниях р и», получим —Ap/Av = yp/v (у = C

) и, следовательно,

D=Yvpv7 (51.5)

Последняя формула представляет собой известную формулу Лапласа

для скорости звука. Таким образом, при малых изменениях р и v скорость

распространения ударных волн должна быть близкой к скорости звука.

Состояние газа в ударной волне, наряду с уравнениями (51.1) и (51.2),

определяется также законом сохранения энергии

+ ^- +

= E-{-^

+ pv, (51.6)

где Е — внутренняя энергия единицы массы газа. Уравнение (51.6) при

помощи (51.1) и (51.2) может быть преобразовано к виду:

— Eo

U(p +

po)(v

—

(51.7)

или, вследствие

Т'

dT = a

(T'-T

То

к виду:

(Т* - То) - 1/а сР' + ро) (vo - v'). (51.8)

Уравнение (51.7), носящее название адиабаты Гюгонъо, при мало раз-

личающихся р и р

и соответственно v и v

в пределе переходит в уравне-

ние адиабаты Пуассона

dE =

—

pdv,

которая отвечает изоэнтропическому процессу.

Следовательно, условия в ударной волне, вообще говоря, отличаются от

изоэнтропических, причем в тем большей степени, чем больше различают-

ся между собой давления и удельные объемы холодного и нагретого газа.

Причина неизоэнтропичности процессов, протекающих в ударной вол-

не,— это их необратимость, обусловленная конечной скоростью измене-

ния состояния газа. Одним из следствий неизоэнтропичности является то,

что газ в ударной волне нагревается значительно сильнее, чем при изо-

энтропическом сжатии до того же давления. Непосредственная причина

дополнительного разогрева заключается в быстром сжатии газа потоком

отходящих горячих газов.

При наличии химической реакции, идущей в волне горения, сопровож-

дающей ударную волну, внутренняя энергия газа кроме энергии сжатия

включает в себя также химическую энергию, выделяющуюся в резуль-

тате реакции. Обозначив энергию, выделяющуюся при превращении 1 г

вещества, через L, в этом случае вместо уравнений (51.7) и (51.8) будем

иметь:

Е -

Ео

= jj C

dT = 1/2

(Р

ро) (vo

-v) + L. (51.9)

То

Поскольку получающаяся из общих законов сохранения формула

(51.3) для скорости ударной волны содержит только величины, характери-

зующие начальное и конечное состояние газа и не использует уравнения

сохранения энергии (51.7) или (51.9), эта формула, очевидно, сохранится

и в том случае, когда ударная волна сопровождается распространяющей-

ся с той же скоростью волной горения. Другими словами, формула, вы-

ражающая скорость детонационной волны, должна быть аналогична фор-

муле (51.3). Различие обеих формул состоит лишь в том, что в ударной

волне конечное состояние газа, определяется величинами р' и г?', отве-

чающими входящей в уравнение (51.8) температуре ТВ детонационной

же волне конечное состояние газа, являющееся состоянием продуктов

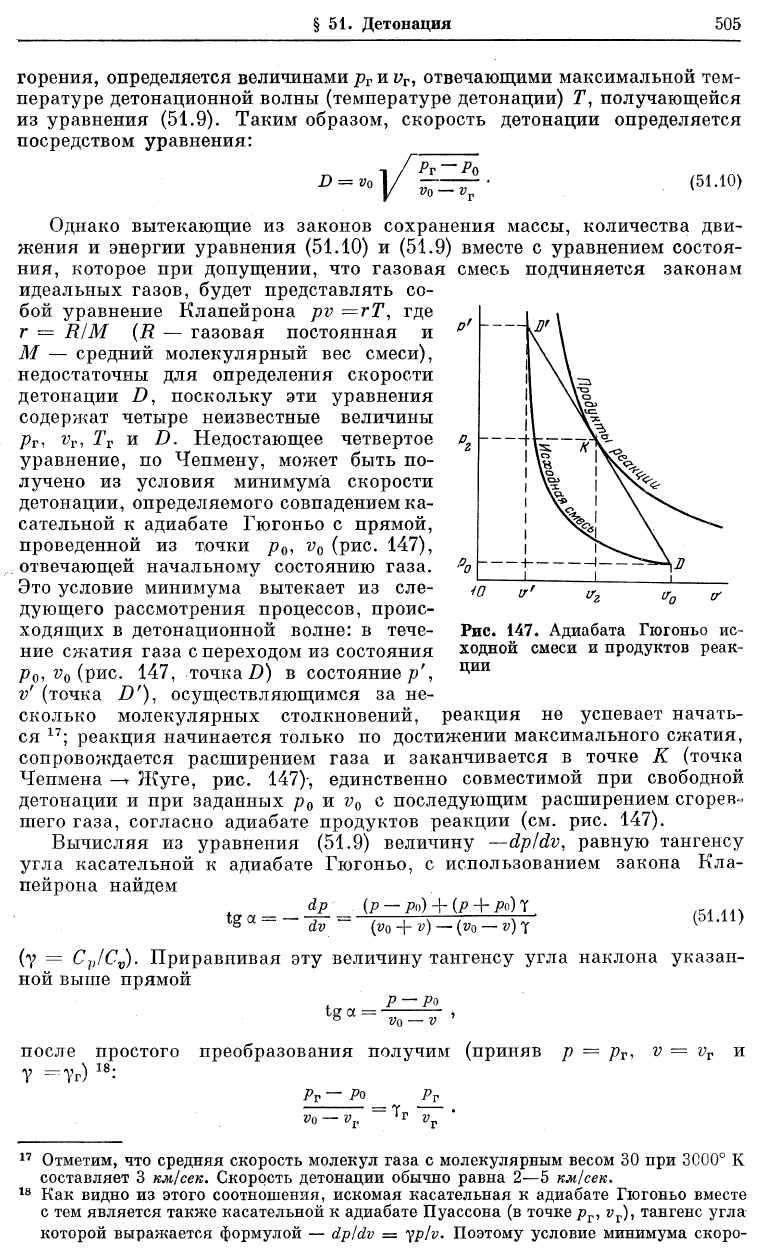
горения, определяется величинами

и у

, отвечающими максимальной тем-

пературе детонационной волны (температуре детонации) Т

, получающейся

из уравнения (51.9). Таким образом, скорость детонации определяется

посредством уравнения:

Рг-Ро

Vo — V

(51.10)

Однако вытекающие из законов сохранения массы, количества дви-

жения и энергии уравнения (51.10) и (51.9) вместе с уравнением состоя-

ния, которое при допущении, что газовая смесь подчиняется законам

идеальных газов, будет представлять со-

бой уравнение Клапейрона pv =гТ, где

г = R/M (R — газовая постоянная и

М — средний молекулярный вес смеси),

недостаточны для определения скорости

детонации Z), поскольку эти уравнения

содержат четыре неизвестные величины

Рт, v

, T

и D. Недостающее четвертое

уравнение, по Чепмену, может быть по-

лучено из условия минимума скорости

детонации, определяемого совпадением ка-

сательной к адиабате Гюгоньо с прямой,

проведенной из точки /?

, v

(рис. 147),

отвечающей начальному состоянию газа.

Это условие минимума вытекает из сле-

дующего рассмотрения процессов, проис-

ходящих в детонационной волне: в тече-

ние сжатия газа с переходом из состояния

, v

(рис. 147, точка/)) в состояние //,

v' (точка £)'), осуществляющимся за не-

сколько молекулярных столкновений, реакция не успевает начать-

ся

; реакция начинается только по достижении максимального сжатия,

сопровождается расширением газа и заканчивается в точке К (точка

Чепмена

—*

Жуге, рис. 147), единственно совместимой при свободной

детонации и при заданных р

и ?;

с последующим расширением сгорев-

шего газа, согласно адиабате продуктов реакции (см. рис. 147).

Вычисляя из уравнения (51.9) величину —dpldv, равную тангенсу

угла касательной к адиабате Гюгоньо, с использованием закона Кла-

пейрона найдем

(Р — ро)

{р

ро) Т ,

(у = C

). Приравнивая эту величину тангенсу угла наклона указан-

ной выше прямой

Р — Ро

tg а = ,

VQ —

после простого преобразования получим (приняв р

У =Чг)

Рис. 147. Адиабата Гюгоньо ис-

ходной смеси и продуктов реак-

ции

, v — v

Ро

Vq — V

= Т

Г «

Отметим, что средняя скорость молекул газа с молекулярным весом 30 при 3000° К

составляет 3 км/сек. Скорость детонации обычно равна 2—5 км/сек.

Как видно из этого соотношения, искомая касательная к адиабате Гюгоньо вместе

с тем является также касательной к адиабате Пуассона (в точке г;

), тангенс угла

которой выражается формулой — dpldv = yplv. Поэтому условие минимума скоро-

Вводя степень сжатия е = vjv

и исключая величины р

и при по-

мощи равенств p

= г

и p

= r

(г

= R!M

, r

= R/M

) из

уравнений (51.9) — (51.11), преобразуем эти уравнения к виду:

'Д. = в/т

, (51.12)

. J = (51.13)

Го

- (Т

1) е

+• гоГо/г

= 0. (51.14)

Из этих трех уравнений и могут быть вычислены три неизвестные величи-

ны: D, е и Т

. Заметим, что вследствие зависимости величины C

от

температуры у

— у

{Т

), эти вычисления не сводятся к простому реше-

нию системы трех алгебраических уравнений, а проводятся по методу

последовательных приближений. Вычисления усложняются также необ-

ходимостью учета диссоциации продуктов горения, особенно существен-

ной при высоких температурах.

Изложенная классическая теория детонации была создана Зель-

довичем [115, 117, 123] в 1940 г. (см. также фон Нейман [1287], Деринг

1713], Гриб [76]) на основе одномерной модели устойчивой детонационной

волны. Позднейшие исследования показали (литературу см. в обзоре Стре-

лова [1554], см. также [49]), что действительная газокинетическая и хи-

мико-кинетическая картина детонационной волны гораздо сложнее той

идеализированной картины плоской ударной волны и плоского фронта

химической реакции, которая следует из классической теории и которая

к тому же оказывается неустойчивой, что приводит к изломам и искривле-

нию волнового фронта и связанным с этим нарушениям идеальной кар-

тины детонационных волн.

Было установлено также, что структура детонационной волны сущест-

венным образом влияет на скорость детонации, что существуют так назы-

ваемые сильная и слабая детонации, распространяющиеся со скоростями,

отличными от скорости классических детонационных волн Ченмена —

Жуге, что имеет место взаимосвязь между интенсивностью иниции-

рующей ударной волны и кинетикой химической реакции и т. д.

Все эти особенности детонационных волн не были известны класси-

ческой теории. Поэтому последняя не в состоянии описать все многообра-

зие реально существующих детонационных волн. Пути построения более

совершенной теории детонации в настоящее время только ещз наме-

чаются [1554]. Однако во многих случаях классическая детонационная волна

Чепмена — Жуге оказывается в достаточной мере адекватной наблю-

даемым фактам, что имеет место при оперировании средними величинами

(благодаря чему остается правильной теория скорости детонации и ряд

других положений классической теории).

Это, в частности, можно иллюстрировать сопоставлением вычислен-

ных на основании классической теории и измеренных значений скорости

детонации в смесях Н

— 0

— N

, приведенных в табл. 35. В этой табли-

це, кроме скоростей детонации приводятся значения максимальных дав-

лений и температур (р

и Т

) в детонационной волне, вычисленные (как

и скорости детонации) [1150] по экспериментальным данным [702, 1341],

а также содержание гидроксила и атомарного водорода в сгоревшем

газе, отвечающее равновесиям Н

0 ^ V

+ ОН и Н

^ 2Н.

сти детонации иногда формулируется как условие касания указанной выше прямой

и адиабаты Пуассона или как условие касания адиабаты Пуассона и адиабаты Гюго-

ньо.

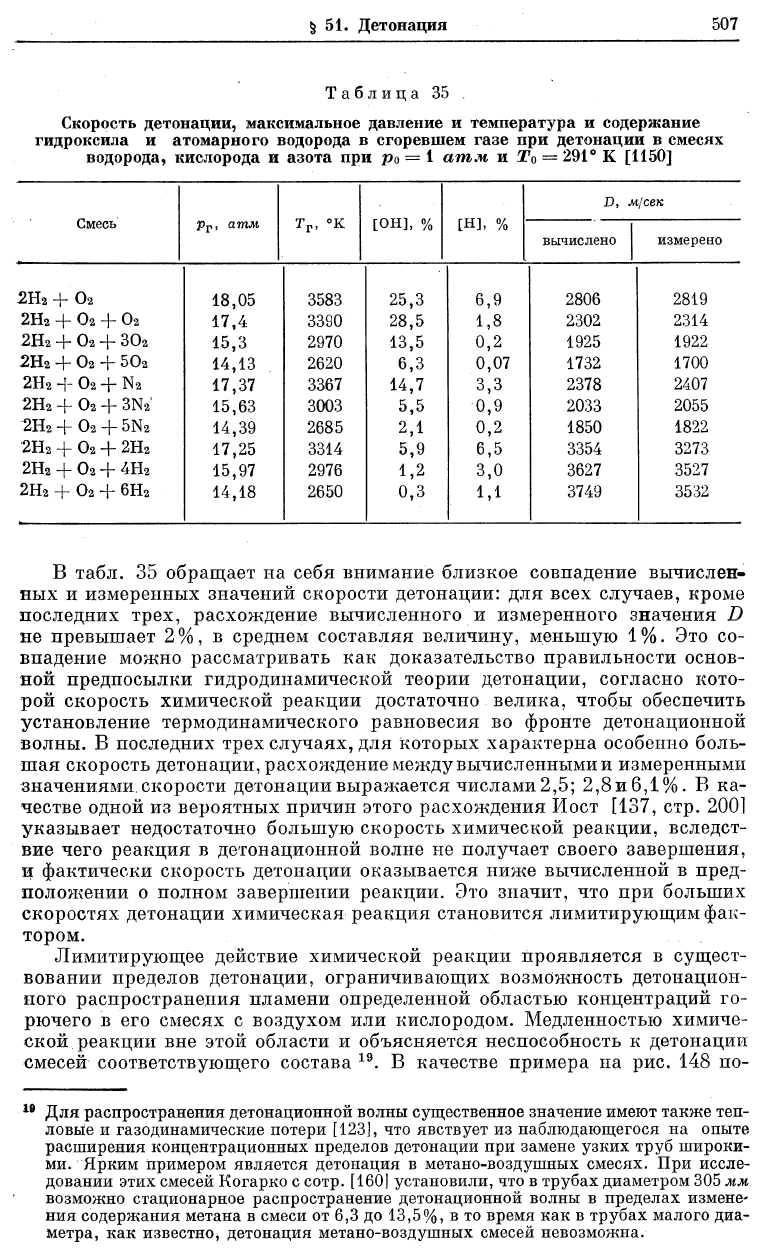
Таблица 35

Скорость детонации, максимальное давление и температура и содержание

гидроксила и атомарного водорода в сгоревшем газе при детонации в смесях

водорода, кислорода и азота при ро = 1 ашм и Т

= 291° К [1150]

D, м/сек

Смесь

, атм

, °к

[ОН], о/о

[H], % '

вычислено измерено

ЗН

+ 0

18,05

3583

25,3 6,9

2806 2819

2Н

+ 0

17,4

3390 28,5

1,8

2302 2314

2Н

+ 0

+ 30

15,3

2970 13,5

0,2

1925

1922

2Н

+ 0

+ 50

14,13

2620

6,3

0,07

1732

1700

2Н

+ 0

+ N

17,37

3367

14,7

3,3

2378

2407

2Н

+ 0

+ 3N

15,63

3003 5,5 0,9

2033

2055

2Н

+ 0

+ 5N

14,39

2685

2Д

0,2 1850

1822

2Н

+ 0

+ 2Н

17,25

3314 5,9 6,5 3354

3273

2Н

+ 0

+ 4Н

15,97

2976

1,2

3,0 3627

3527

2На + 0а + 6На

14,18

2650

0,3

1,1

3749

3532

В табл. 35 обращает на себя внимание близкое совпадение вычислен-

ных и измеренных значений скорости детонации: для всех случаев, кроме

последних трех, расхождение вычисленного и измеренного значения D

не превышает 2%, в среднем составляя величину, меньшую 1%. Это со-

впадение можно рассматривать как доказательство правильности основ-

ной предпосылки гидродинамической теории детонации, согласно кото-

рой скорость химической реакции достаточно велика, чтобы обеспечить

установление термодинамического равновесия во фронте детонационной

волны. В последних трех случаях, для которых характерна особенно боль-

шая скорость детонации, расхождение между вычисленными и измеренными

значениями, скорости детонации выражается числами 2,5; 2,8и6,1%. В ка-

честве одной из вероятных причин этого расхождения Иост [137, стр. 200]

указывает недостаточно большую скорость химической реакции, вследст-

вие чего реакция в детонационной волне не получает своего завершения,

и фактически скорость детонации оказывается ниже вычисленной в пред-

положении о полном завершении реакции. Это значит, что при больших

скоростях детонации химическая реакция становится лимитирующим фак-

тором.

Лимитирующее действие химической реакции проявляется в сущест-

вовании пределов детонации, ограничивающих возможность детонацион-

ного распространения пламени определенной областью концентраций го-

рючего в его смесях с воздухом или кислородом. Медленностью химиче-

ской реакции вне этой области и объясняется неспособность к детонации

смесей соответствующего состава

. В качестве примера на рис. 148 по-

Для распространения детонационной волны существенное значение имеют также теп-

ловые и газодинамические потери [123], что явствует из наблюдающегося на опыте

расширения концентрационных пределов детонации при замене узких труб широки-

ми. Ярким примером является детонация в метано-воздушных смесях. При иссле-

довании этих смесей Когарко с сотр. [160] установили, что в трубах диаметром 305 мм

возможно стационарное распространение детонационной волны в пределах измене-

ния содержания метана в смеси от 6,3 до 13,5%, в то время как в трубах малого диа-

метра, как известно, детонация метано-воздушных смесей невозможна.

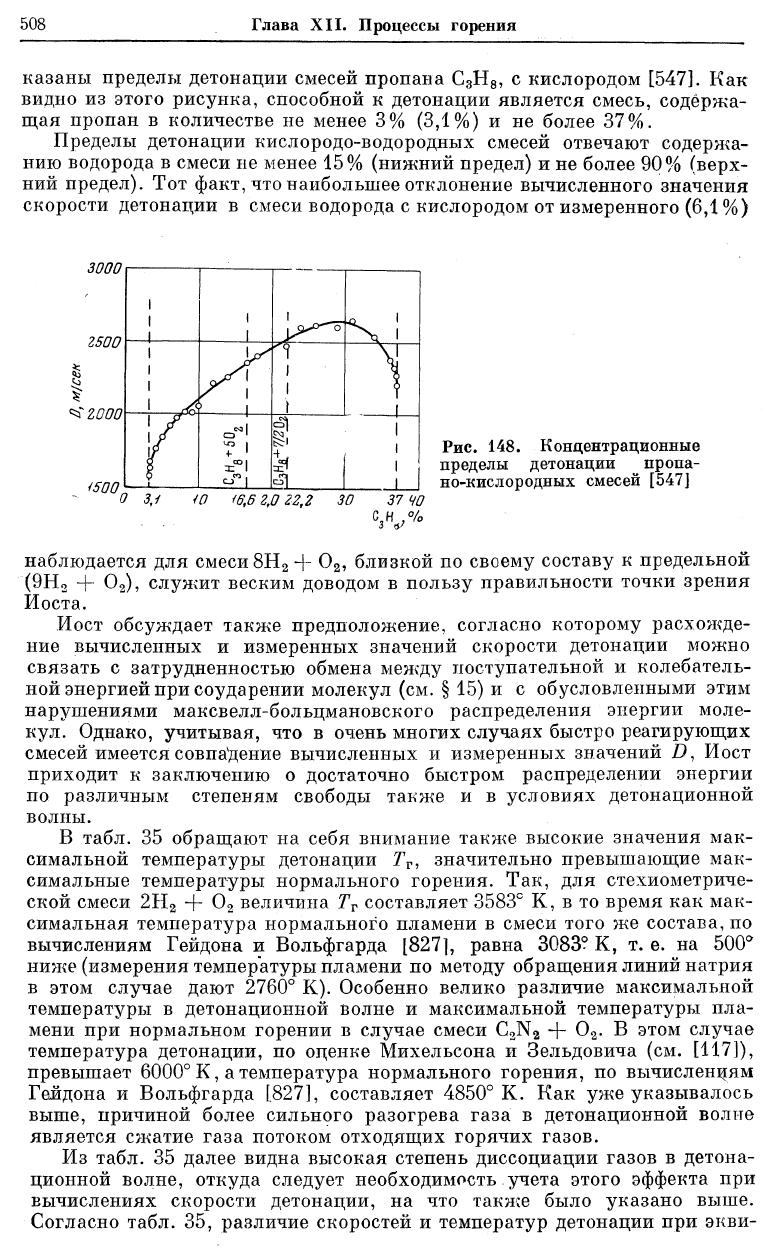
казаны пределы детонации смесей пропана С

, с кислородом [547]. Как

видно из этого рисунка, способной к детонации является смесь, содержа-

щая пропан в количестве не менее 3% (3,1%) и не более 37%.

Пределы детонации кислородо-водородных смесей отвечают содержа-

нию водорода в смеси не менее 15% (нижний предел) и не более 90% (верх-

ний предел). Тот факт, что наибольшее отклонение вычисленного значения

скорости детонации в смеси водорода с кислородом от измеренного (6,1 %)

наблюдается для смеси 8Н

+ 0

, близкой по своему составу к предельной

(9Н

+ 0

), служит веским доводом в пользу правильности точки зрения

Поста.

Иост обсуждает также предположение, согласно которому расхожде-

ние вычисленных и измеренных значений скорости детонации можно

связать с затрудненностью обмена между поступательной и колебатель-

ной энергией при соударении молекул (см. § 15) и с обусловленными этим

нарушениями максвелл-больцмановского распределения энергии моле-

кул. Однако, учитывая, что в очень многих случаях быстро реагирующих

смесей имеется совпадение вычисленных и измеренных значений Z), Иост

приходит к заключению о достаточно быстром распределении энергии

по различным степеням свободы также и в условиях детонационной

волны.

В табл. 35 обращают на себя внимание также высокие значения мак-

симальной температуры детонации Г

, значительно превышающие мак-

симальные температуры нормального горения. Так, для стехиометриче-

ской смеси 2Н

+ 0

величина Т

составляет 3583° К, в то время как мак-

симальная температура нормального пламени в смеси того же состава, по

вычислениям Гейдона и Вольфгарда [827], равна 3083? К, т. е. на 500°

ниже (измерения температуры пламени по методу обращения линий натрия

в этом случае дают 2760° К). Особенно велико различие максимальной

температуры в детонационной волне и максимальной температуры пла-

мени при нормальном горении в случае смеси C

+ 0

. В этом случае

температура детонации, по оценке Михельсона и Зельдовича (см. [117]),

превышает 6000° К, а температура нормального горения, по вычислениям

Гелдона и Вольфгарда [827], составляет 4850° К. Как уже указывалось

выше, причиной более сильного разогрева газа в детонационной волне

является сжатие газа потоком отходящих горячих газов.

Из табл. 35 далее видна высокая степень диссоциации газов в детона-

ционной волне, откуда следует необходимость учета этого эффекта при

вычислениях скорости детонации, на что также было указано выше.

Согласно табл. 35, различие скоростей и температур детонации при экви-

валентной замене кислорода азотом должно быть обусловлено главным об-

разом различием в степени диссоциации смесей. Действительно, количест-

во молекул воды, дающих при диссоциации гидроксил, согласно схеме

0 +

-^20Н, ИЗ которой следует р

я/рн

о — Рщо Vpo

, увеличи-

вается с возрастанием содержания кислорода в смеси, что и наблюдается

в действительности. Одновременное уменьшение содержания воды, даю-

щей при диссоциации атомарный водород, следует из отвечающей урав-

нению Н

0 ^ 2Н + V

зависимости рц/рн

о Ря

о/УРо

- В результа-

те дополнительного поглощения энергии, расходуемой на увеличение

диссоциации, температура детонации при избытке кислорода понижает-

ся, что и приводит к уменьшению скорости детонации.

Аналогичная картина наблюдается также в случае детонации смесей

, 0

и N

, где увеличение скорости и температуры детонации при за-

мене кислорода азотом объясняется происходящим при этом уменьшением

степени диссоциации кислорода. Так, при переходе от смеси G

+ 30

к смеси C

+ 0

+ 2N

, согласно вычислениям Зельдовича ]117],

скорость и температура детонации увеличиваются соответственно от 2135

до 2265 м/сек и от 4095 до 4395° К. Измеренные значения скорости дето-

нации равны: для первой смеси 2110 м/сек (Диксон), для второй смеси

2165 м!сек (Диксон) и 2230 м!сек (Кемпбелл) (см. [117]).

В связи с данными табл. 35 отметим также сравнительно высокие

значения максимального давления в детонационной войне. Однако не-

смотря на это, вследствие высокой температуры, степень сжатия газа в

детонационной волне невелика

и доставляет величину, близкую к 2.

Выше, при обсуждении приведенных в табл. 35 данных, следуя Иосту,

мы пришли к заключению о необходимости учета скорости химической реак-

ции в детонационной волне в случае смесей состава, близкого к предель-

ному, когда недостаточно большая скорость реакции горения становится

лимитирующим фактором. Указания на связь между скоростью детона-

ции и скоростью и механизмом химических реакций имеются также и в

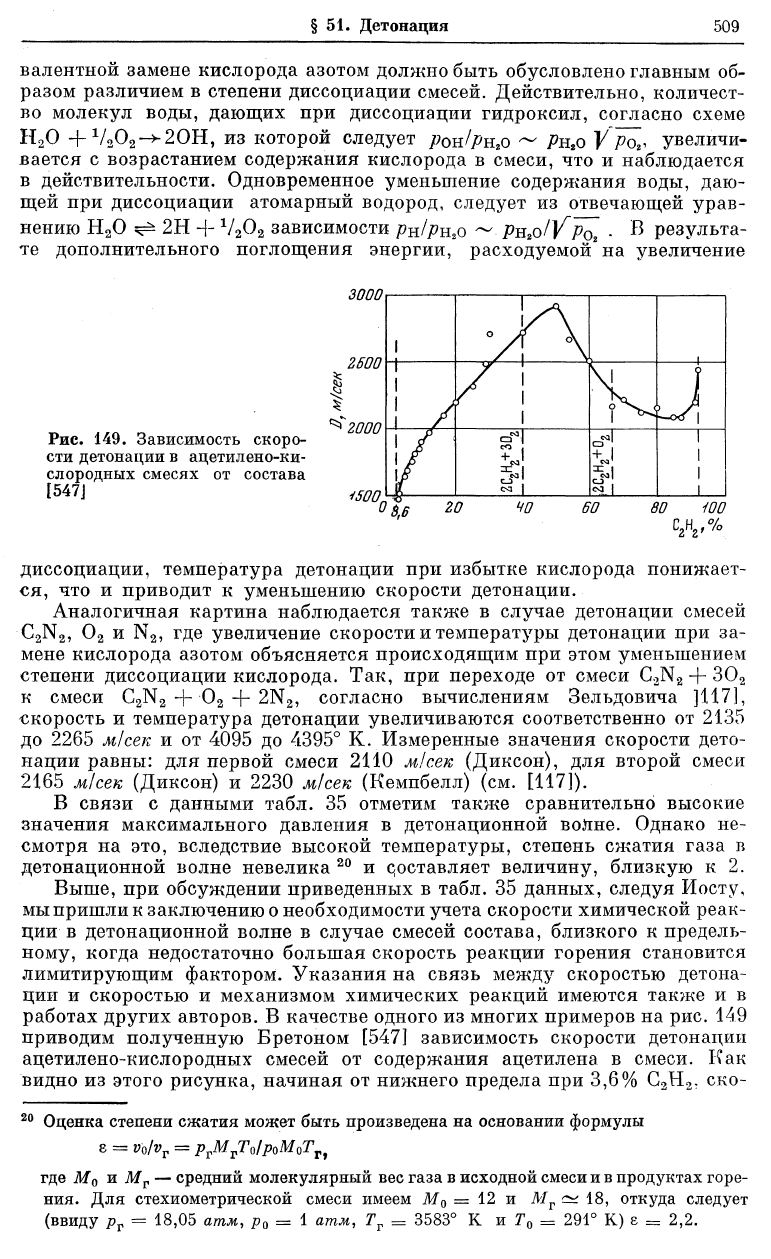
работах других авторов. В качестве одного из многих примеров на рис. 149

приводим полученную Бретоном [547] зависимость скорости детонации

ацетилено-кислородных смесей от содержания ацетилена в смеси. Как

видно из этого рисунка, начиная от нижнего предела при 3,6% С

. ско-

Оценка степени сжатия может быть произведена на основании формулы

= v

= р

/р0М

тf

где Мо и М

— средний молекулярный вес газа в исходной смеси и в продуктах горе-

ния. Для стехиометрической смеси имеем М

= 12 и М

~ 18, откуда следует

(ввиду p

= 18,05 атм, p

= 1 атм, Т

= 3583° К и Т

= 291° К) 8 = 2,2.

рость детонации растет, достигает максимума при 50%, после чего умень~

шается, с тем чтобы, пройдя через минимум около 85% С

, дать резкое

возрастание вплоть до верхнего предела детонации, лежащего около 92—

93% С

. Согласно Бретону и Лаффиту (см. Иост [137, стр. 210—211]),

такой необычный ход кривой пределов детонации обусловлен двумя раз-

личными химическими реакциями: реакцией горения ацетилена, преоб-

ладающей при малых концентрациях последнего, и реакцией взрывного^

крекинга ацетилена, являющейся основной реакцией при высоких кон-

центрациях С

, стимулируемой его сгоранием.

Вопрос о взаимосвязи между детонацией и обусловливающей ее хими-

ческой реакцией наиболее четкую постановку впервые получил в работах

Зельдовича [117], который дал и наиболее удовлетворительное его решение

(см. также [713, 717, 960. 1287]). Зельдович прежде всего четко сформу-

лировал положение о прямой связи механизма детонационного распрост-

ранения пламени с реакцией горения. Отправным пунктом здесь служит

высказывавшееся различными авторами утверждение, что механизм рас-

пространения детонации заключается в передаче давления от слоя к

слою, приводящего к воспламенению газа. Зельдовичем совместно со

Шляпинтохом [129] было дано прямое экспериментальное доказательства

возможности воспламенения газа при сжатии его ударной волной (про-

изводимой в горючей смеси пулей, летящей со сверхзвуковой скоростью).

В непосредственной близости от фронта ударной волны происходит

воспламенение сжатого газа, и так как вследствие большой скорости

распространения ударной волны диффузия (как и теплопроводность)

не играет сколько-нибудь существенной роли

, то в реакцию вступает

смесь, не разбавленная продуктами реакции и не содержащая активных

центров, образовавшихся в соседних слоях газа в предшествующие мо-

менты времени. По этой причине воспламенение горючей смеси в ударной

волне должно ближе соответствовать самовоспламенению газа в статиче-

ских условиях, чем воспламенению при нормальном горении (где переда-

ча тепла теплопроводностью и диффузия активных центров играют

основную роль). Экспериментальным (качественным) доказательством пра-

вильности этих представлений являются данные по влиянию неболь-

ших концентраций активных примесей, полученные в работах Соколика

[322], Ривина и др. [38, 293]. Из этих работ, в частности, следует, что

активные примеси одинаково расширяют концентрационные пределы де-

тонации (не влияя, однако, на скорость детонации), так же как расширя-

ют пределы и ускоряют самовоспламенение тех лее смесей в статических

условиях.

Одним из наиболее убедительных экспериментальных доказательств

правильности представления о том, что поджигание горючей смеси удар-

ной волной представляет собой чисто тепловой эффект, является резуль-

тат опытов Штейнберга и Каскана [1539], измерявших температуру са-

мовоспламенения и температуру воспламенения в ударной волне смесей

водорода с кислородом и пропана С

с воздухом. Так, для смеси 2Н

+ 0

они получили температуру самовоспламенения 760—740° К (при дав-

лении 5—7,5

атпм)

и температуру воспламенения в ударной волне 800° К.

Температура воспламенения этой смеси адиабатическим сжатием, по дан-

ным различных авторов, составляет 820—800° К.

В смеси, воспламенившейся в результате сжатия ударной волной, раз-

вивается химическая реакция горения, осуществляющаяся при постоян-

ной скорости распространения. Последнее обстоятельство приводит к вы-

текающему из уравнения (51.10) линейному закону изменения состоя-

См., однако, работу [655].