Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.


ε
1
ε
2

˙x(t)=σy − σx;
˙y(t)=−y + rx − xz;
˙z(t)=−bz + xy,
r
u
1
˙x(t)=σy − σx + u
1
;
˙y(t)=−y + rx − xz;
˙z(t)=−bz + xy.
u
1
u
1
(x, y, z)
u
1
(x, y, z)
u
1
(x, y, z)
r σ b
ψ
1
(x, y, z)
ψ
1
=0
T
1
˙
ψ
1
(t)+ψ
1
=0,
T
1
> 0 ψ
1
(t)=ψ
0
e
−
t
T
1
(t →∞) ψ
1
=0
(4 ÷ 5)T
1
ψ
0
(x
0
,y
0
,z
0
)
ψ
1
= x + βy.

ψ
1
u
1
= −(βr − σ)x − (σ − β)y + βxz −
1
T
1
ψ
1
,
ψ
1
=0
x = −βy
˙y
ψ
(t)=−y
ψ
− rβy
ψ
+ βy
ψ
z
ψ
;
˙z
ψ
(t)=−bz
ψ
− βy
2
ψ
,
ψ
1
=0
y
s
= z
s
=0
V
ψ
=0, 5y
2
ψ
+0, 5z
2
ψ
> 0.
˙
V
ψ
(t)=−(1 + rβ)y
2
− bz
2
< 0.
˙
V
ψ
(t)
y
s
=
z
s
=0
˙
V
ψ
(t) < 0
r>0; b>0; β>0.
ψ
1
=0 x = −βy x
s
=0
u
1
T
1
> 0
x
s
= y
s
= z
s
=0
r σ b
σ =10
b =8/3 r =24 β =2
β =2
β β = −β
0

˙y
ψ
(t)=(β
0
r − 1)y
ψ
− β
0
y
ψ
z
ψ
;
˙z
ψ
(t)=−bz
ψ
+ β
0
y
2
ψ
.
λ = β
0
r −1 β
0
=
1
r β
0
r<1 λ<0
y
s
= z
s
=0 β
0
r>1 λ>0
˙y
ψ
(t)
∼
=
λy
ψ
−
β
2
0
b
y
3
ψ
;˙z
ψ
(t) ≈ 0.
λ =0
λ =0
y
s
= ±
1
β
0
√
bλ = ±
1
β
0
b(β
0
r − 1)
x
s
= ±
b(β
0
r − 1); z
s
=
β
0
r − 1
β
0
.
σ =10
b =8/3 r =24 β = −2
β = −2
r>1
β>0 β<0
β<0 ψ
1
=0

u
3
˙x(t)=σy − σx;
˙y(t)=−y + rx − xz;
˙z(t)=−bz + xy + u
3
.
ψ
3
= z − γ − ηx
2
.
ψ
3
T
3
˙
ψ
3
(t)+ψ
3
=0.
˙x(t) ˙z(t)
u
3
=(2ησ − 1)xy + bz +2ησx
2
−
1
T
3
ψ
3
,
ψ
3
=0
(4 ÷ 5)T
3
z = γ + ηx
2
˙x
ψ
(t)=σy
ψ
− σx
ψ
;
˙y
ψ
(t)=−y
ψ
+ rx
ψ
−
γ + ηx
2
ψ
x
ψ
,
ψ
3
=0
x
ψ
1
σ
¨x
ψ
(t)+
1+
1
σ
˙x
ψ
(t)=(r −1 − γ)x
ψ
− ηx
3
ψ
.
γ r η 0
x
ψ
=0 γ = r η =0
1
σ
¨x
ψ
(t)+
1+
1
σ
˙x
ψ
(t)+x
ψ
=0.
x(t) → 0 σ>0 t →∞
ηx
3
ψ
γ r η 0
x
s
=0; y
s
=0; z
s
= γ.
0 γ r − 1 η>0
r
c
=1+γ
x
s
= ±
r − 1 −γ
η
.

x
s
= y
s
= ±
r − 1 − γ
η
; z
s
= r − 1,
γ =0 η =
1
b
˙y(t) ≈ 0
y
ψ
=(r − γ)x
ψ
− ηx
3
ψ
.
y
ψ
˙x
ψ
(t)=σ(r − γ − 1)x
ψ
− σηx
3
ψ
.
˙x
ψ
(t)=λ
1
x
ψ
− λ
2
x
3
ψ
,
λ
1
= σ(r − γ − 1); λ
2
= ση.
u
3
u
3
λ
1
σ =10 b =8/3 r =24 λ
1
> 0 λ
1
< 0
λ
1
= λ
2
=10
λ
1
= −100 λ
2
=70
u
3
γ η

λ
1
> 0 λ
1
< 0
¨x(t)+(σ +1)˙x(t)+σ(1 − z)x + xz =0,
˙z(t)=−bz +
x ˙x(t)
σ
+ x
2
+ u.
ψ
4
= z − γ − αx
2
+ βσ(y − x)x.
ψ
4
T
4
˙
ψ
4
(t)+ψ
4
=0,
u
3
= bz + xy + σ(y − x)(2α +2βσx −βσy) − βσx(rx − y + xz) −
1
T
4
ψ
4
.
ψ
4
=0 x
¨x
ψ
(t)+(σ +1− βx
2
ψ
)˙x
ψ
(t)+(γ + σ − σr)x
ψ
+ αx
3
ψ
=0.
σ r α β γ
σ =10 r =28 b =
8
3
α = 100
β =10 γ =15 T
4
=0, 1
x y z
u
3
u
1
u
3
u
3
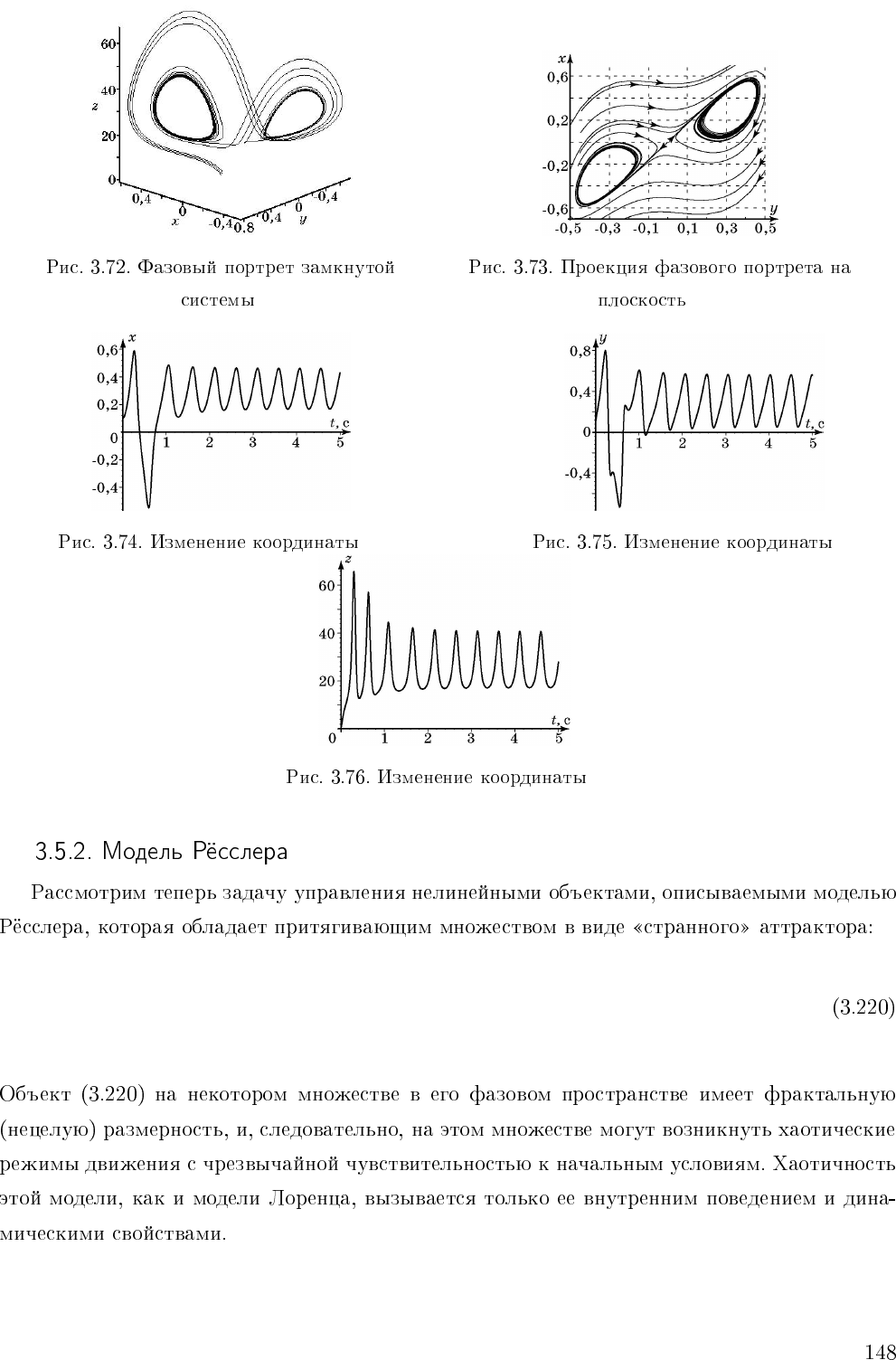
xy
x y
z
˙x
1
(t)=−x
2
− x
3
;
˙x
2
(t)=x
1
+ ax
2
;
˙x
3
(t)=bx
1
+ x
1
x
3
− cx
3
.

˙x
1
(t)=−x
2
− x
3
+ u
1
;
˙x
2
(t)=x
1
+ ax
2
;
˙x
3
(t)=bx
1
+ x
1
x
3
− cx
3
.
ψ
1
= x
1
− γx
2
+ βx
m
2
,
T
1
˙
ψ
1
(t)+ψ
1
=0,
u
1
= x
2
+ x
3
−
γ − βmx
m−1
2
x
1
+ ax
2
−
1
T
1
ψ
1
.
u
1
ψ
1
=0
˙x
2ψ
(t)=γx
2ψ
+ ax
2ψ
− βx
m
2ψ
;
˙x
3ψ
(t)=
b + x
3ψ
γx
2ψ
− βx
m
2ψ
− cx
3ψ
.
γ λ m
γ<0 |γ| >a β 0 m =2, 3
x
2ψ
→ 0 x
3ψ
→ 0 x
1ψ
→ 0
x
1s
= x
2s
= x
3s
=0
a =0, 38 b =0, 3 c =4, 82 γ =
−1
β =1 m =2 T =1
γ = −1 m =2
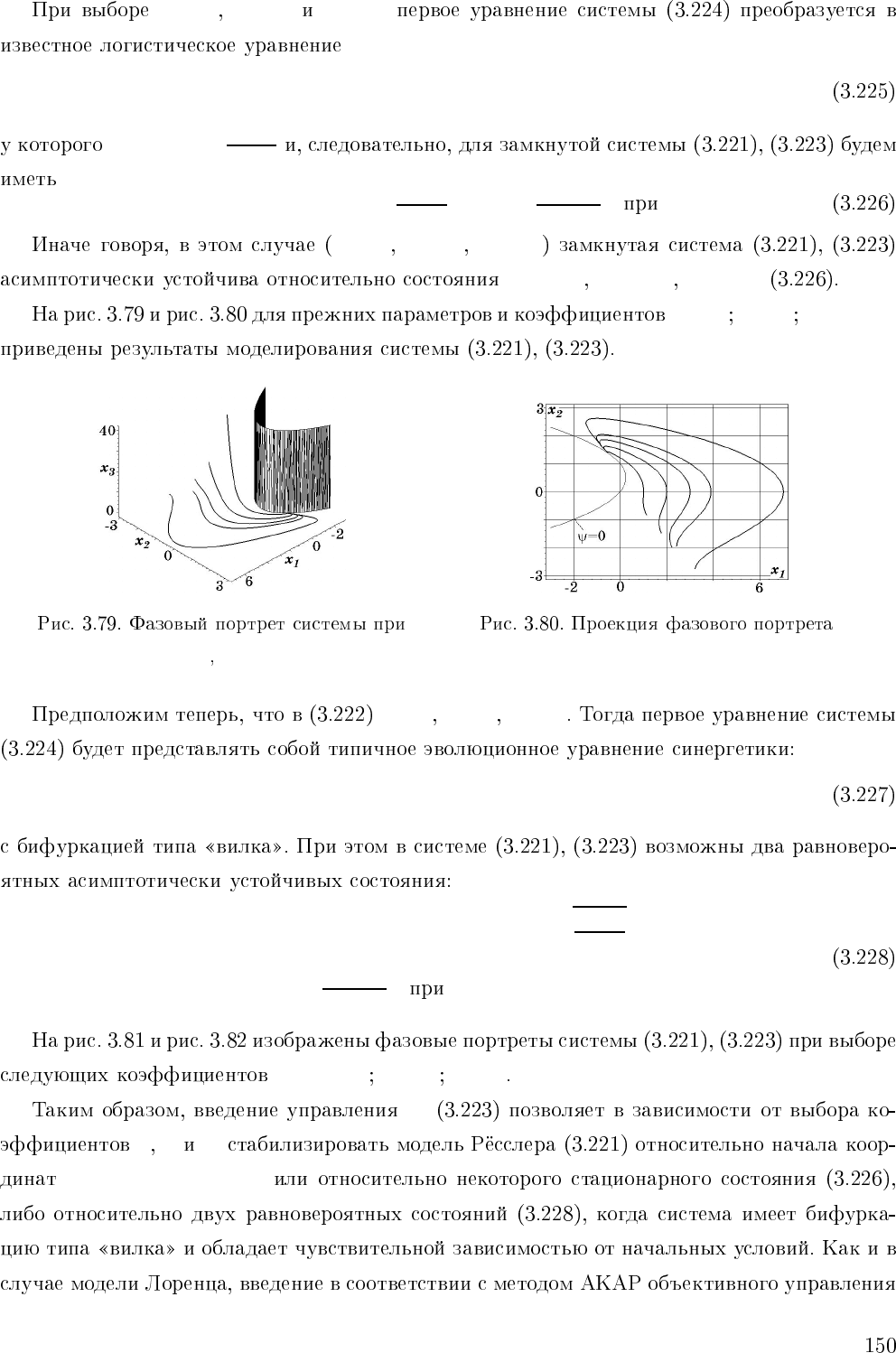
γ>0 β>0 m =2
˙x
2ψ
(t)=(γ + a)x
2ψ
− βx
2
2ψ
,
x
2ψ
= x
2s
=
γ + a
λ
x
1s
= γx
2s
− λx
2
2s
; x
2s
=
γ + a
λ
; x
3s
=
bx
1s
c − x
1s
c>x
1s
.
γ>0 β>0 m =2
x
1
= x
1s
x
2
= x
2s
x
3
= x
3s
m =2 T =1 γ = β =1
γ =1 m =2
γ>0 β>0 m =3
˙x
2ψ
(t)=(γ + a)x
2ψ
− βx
3
2ψ
x
1s
=
γ − βx
2
2s
x
2s
; x
2s
= ±
γ + a
β
;
x
3s
=
bx
1s
c − x
1s
c>|x
1s
|.
γ = β =1 m =3 T =1
u
1
γ β m
x
1s
= x
2s
= x
3s
=0
