Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.


˙x
1
(t)=x
2
;
˙x
2
(t)=(x
3
x
4
− m
l
) a
21
;
˙x
3
(t)=(u
1
− x
2
x
4
− a
31
x
3
) a
32
;
˙x
4
(t)=(u
2
− x
4
) a
41
.
x
1
= γ
∗
x
2
= ω
∗
x
3
= I
∗
x
4
=Φ
∗
u
1
= U
a∗
u
2
= U
e∗
m
l
= M
l∗
f
1
(x
4
)
a
ij
u
1
u
2
ψ
1
= x
3
+ v
1
(x
1
,x
2
)=0;
ψ
2
= x
4
+ v
2
(x
1
,x
2
)=0.
v
1
(x
1
,x
2
) v
2
(x
1
,x
2
)
ψ
1
=0 ψ
2
=0
T
1
˙
ψ
1
(t)+ψ
1
=0;
T
2
˙
ψ
2
(t)+ψ
2
=0,
ψ
1
=0 ψ
2
=0
u
1
=
a
31
−
1
T
1
a
32
x
3
+ x
2
x
4
−
1
T
1
a
32
v
1
−
1
a
32
∂v
1
∂x
1
x
2
+
∂v
1
∂x
2
(x
3
x
4
− m
l
)a
21
;
u
2
=f
1
(x
4
) −
1
T
2
a
41
(x
4
+ v
2
) −
1
a
41
∂v
2
∂x
1
x
2
+
∂v
2
∂x
2
(x
3
x
4
− m
l
)a
21
.
˙x
1ψ
(t)=x
2ψ
;
˙x
2ψ
(t)=(v
1
v
2
− m
l
)a
21
.
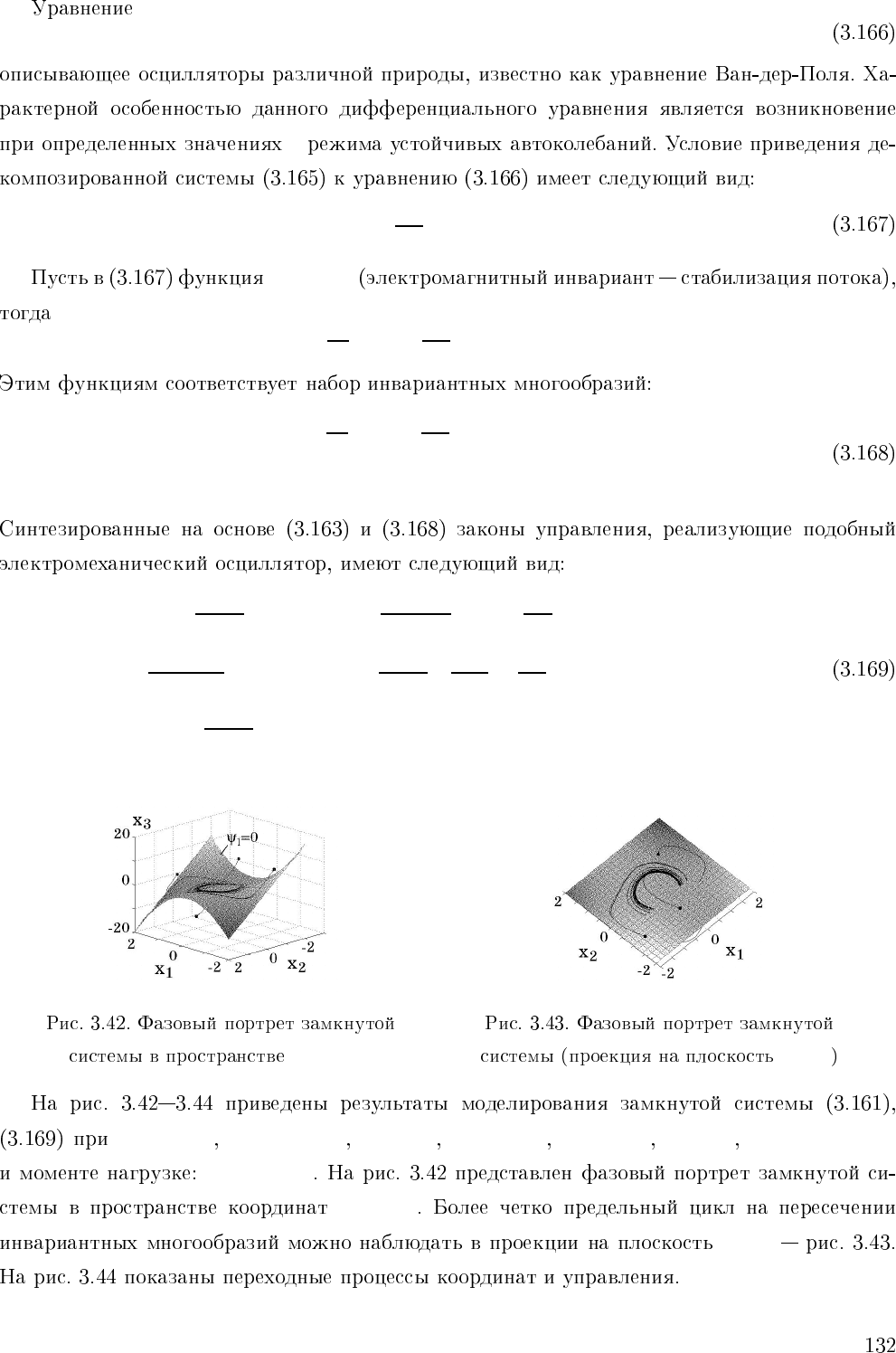
¨x(t) − (ε − x
2
)˙x(t)+x =0,
ε
v
1
v
2
= m
l
+
1
a
21
((ε − x
2
1ψ
)x
2ψ
− x
1ψ
).
v
2
= −x
0
4
v
1
= −
1
x
0
4
m
l
+
1
a
21
((ε − x
2
1
)x
2
− x
1
)
.
ψ
1
= x
3
−
1
x
0
4
m
l
+
1
a
21
((ε − x
2
1
)x
2
− x
1
)
=0,
ψ
2
= x
4
− x
0
4
=0.
u
1
=
a
31
−
1
T
1
a
32
x
3
+ x
2
x
4
+
1
x
0
4
T
1
a
32
m
l
+
1
a
21
((ε − x
2
1
)x
2
− x
1
)
−
−
1
x
0
4
a
21
a
32
(2x
1
x
2
+1)x
2
+
a
21
x
0
4
a
32
∂m
l
∂x
2
+
1
a
21
(ε − x
2
1
)
(x
3
x
4
− m
l
);
u
2
=f
1
(x
4
) −
1
T
2
a
41
(x
4
− x
0
4
).
X
1
X
2
X
3
X
1
X
2
a
21
=0, 5 a
31
=0, 002 a
32
=5 a
41
=1, 7 ε =0, 12 x
0
4
=1 T
1
= T
2
=0, 5
m
l
=0, 5x
2
X
1
X
2
X
3
X
1
X
2

ε =0, 7
ε
ε =0, 7
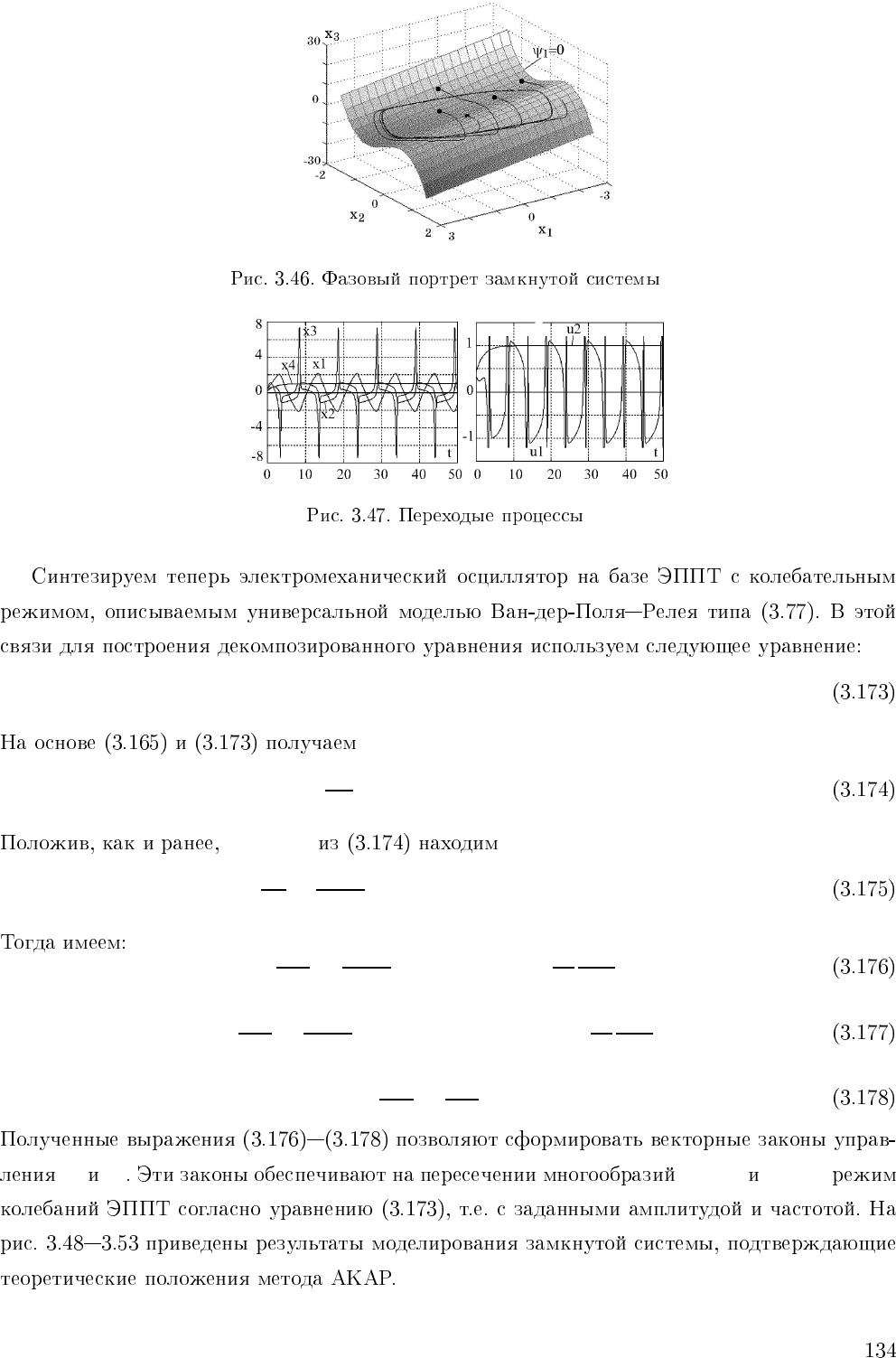
¨x(t) − η(1 − ˙x
2
(t)) ˙x(t)+x =0.
v
1
v
2
= m
l
+
1
a
21
(η(1 −x
2
2ψ
)x
2ψ
− x
1ψ
).
v
2
= −x
0
4
v
1
= −
1
x
0
4
m
l
+
1
a
21
(η(1 − x
2
2
)x
2
− x
1
)
.
u
1
=
a
31
−
1
T
1
a
32
x
3
+
1
x
0
4
T
1
a
32
m
l
+
1
a
21
(η(1 − x
2
2
)x
2
− x
1
)
+
+
1
x
0
4
a
32
a
21
∂m
l
∂x
2
+ η(1 − 3x
2
2
)
(x
3
x
4
− m
l
)+x
2
x
4
−
x
2
x
0
4
a
21
a
32
;
u
2
= f
1
(x
4
) −
1
T
2
a
41
(x
4
− x
0
4
).
X
1
X
2
X
3
T
1
=0, 5 T
2
=2
x
0
4
=1 η =4 m
l
=0, 5x
2
η
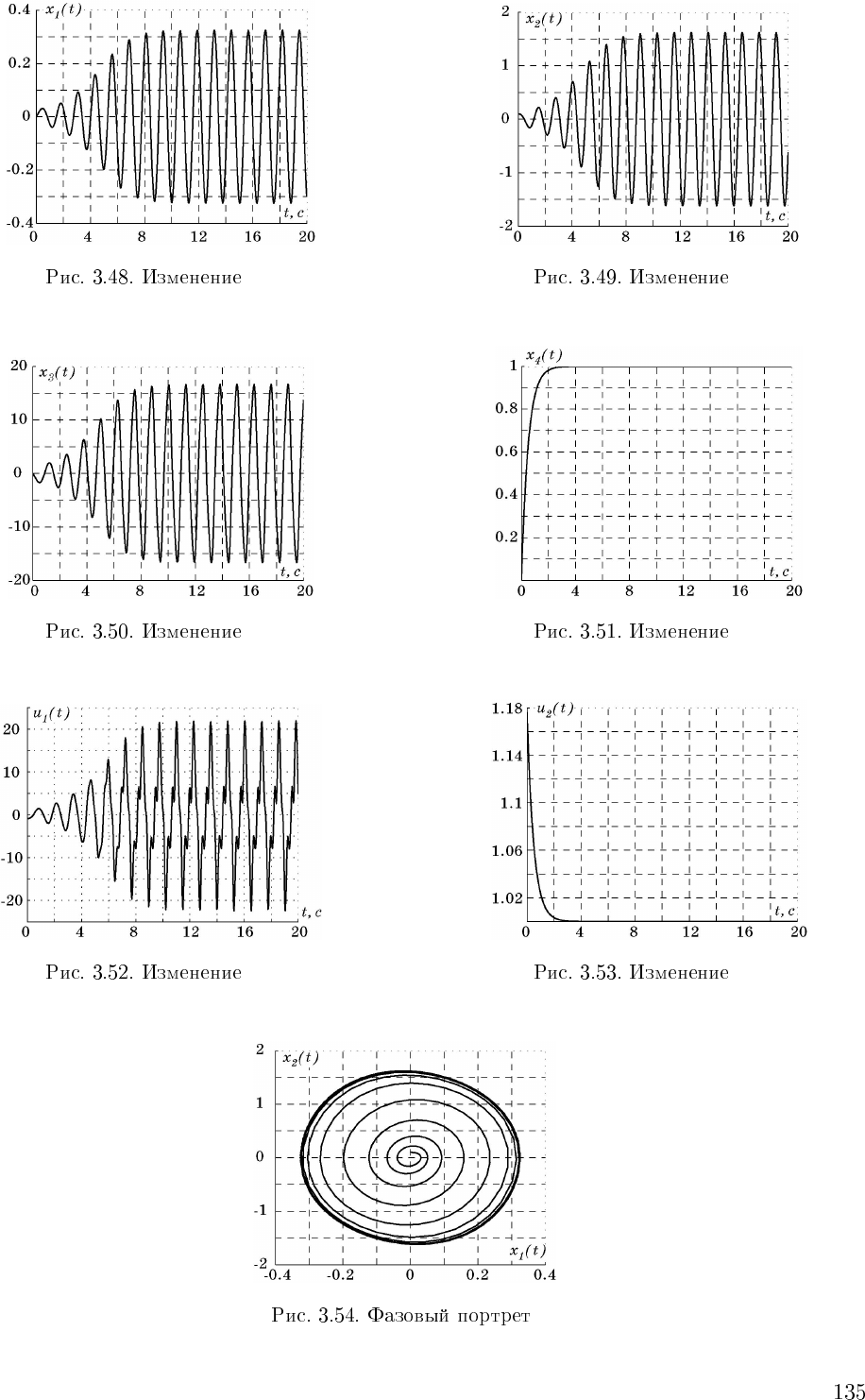
¨x(t) − µ(1 − 0, 5αx
2
− 0, 5β ˙x
2
)˙x(t)+ω
2
x =0
v
1
v
2
= m
l
+
1
a
21
µ(1 − 0, 5αx
2
1
− 0, 5βx
2
2
)x
2
− ω
2
x
1
.
v
2
= −x
0
4
v
1
= −
m
l
x
0
4
−
1
x
0
4
a
21
µ(1 − 0, 5αx
2
1
− 0, 5βx
2
2
)x
2
− ω
2
x
1
.
∂v
1
∂x
1
=
1
x
0
4
a
21
(µαx
1
x
2
+ ω
2
) −
1
x
0
4
∂m
l
∂x
1
;
∂v
1
∂x
2
=
µ
x
0
4
a
21
(0, 5αx
2
1
+1, 5βx
2
2
− 1) −
1
x
0
4
∂m
l
∂x
2
;
∂v
2
∂x
1
=
∂v
2
∂x
2
=0
u
1
u
2
ψ
1
=0 ψ
2
=0
x
1
x
2
x
3
x
4
u
1
u
2

˙x
1
(t)=x
2
;
˙x
2
(t)=
3
2
p
2
L
12
JL
2
x
3
x
5
−
p
J
m
l
(x
2
);
˙x
3
(t)=
r
r
L
12
L
2
x
4
−
r
2
L
2
x
3
;
˙x
4
(t)=−
r
2
L
2
12
+ r
1
L
2
2
L
2
(L
1
L
2
− L
2
12
)
x
4
+ x
2
x
5
+
r
2
L
12
L
2
x
2
5
x
3
+
r
2
L
12
L
2
(L
1
L
2
− L
2
12
)
x
3
+
L
2
L
1
L
2
− L
2
12
u
1
;
˙x
5
(t)=−
r
2
L
2
12
+ r
1
L
2
2
L
2
(L
1
L
2
− L
2
12
)
x
5
+ x
2
x
4
+
r
2
L
12
L
2
x
4
x
5
x
3
+
L
12
L
1
L
2
− L
2
12
x
3
x
2
+
L
2
L
1
L
2
− L
2
12
u
2
.
x
1
x
2
x
3
x
4
x
5
u
1
u
2
m
l
(x
2
)
L
1
L
2
L
12
R
1
R
2
p J
ψ
1
= β
1
x
4
− v
1
(x
1
,x
2
,x
3
)
+ β
2
x
5
− v
2
(x
1
,x
2
,x
3
)
=0;
ψ
2
= β
3
x
4
− v
1
(x
1
,x
2
,x
3
)
+ β
4
x
5
− v
2
(x
1
,x
2
,x
3
)
=0.
˙x
1
(t)=x
2
;
˙x
2
(t)=
3
2
p
2
L
12
JL
2
x
3
ϕ
2
(x
1
,x
2
,x
3
) −
p
J
m
l
(x
2
);
˙x
3
(t)=
r
r
L
12
L
2
ϕ
1
(x
1
,x
2
,x
3
) −
r
2
L
2
x
3
.
ψ
3
= x
3
−x
0
3
=0
T
3
˙
ψ
3
(t)+ψ
3
=0 ϕ
1
(x
1
,x
2
,x
3
)
˙x
1
(t)=x
2
,
˙x
2
(t)=
3
2
p
2
L
12
JL
2
x
0
3
ϕ
2
−
p
J
m
l
(x
2
),

ϕ
2
(x
1
,x
2
,x
3
)
ϕ
1
(x
1
,x
2
,x
3
)=
2
Jx
2
(ε − x
1
) − Jx
1
+ pm
l
(x
2
)
L
2
3p
2
L
12
x
0
3
ϕ
1
(x
1
,x
2
,x
3
) ϕ
2
(x
1
,x
2
,x
3
)
u
1
(x
1
,...,x
5
u
2
(x
1
,...,x
5
r
1
=0, 03 r
2
=0, 0172 L
12
=0, 0154
L
1
= L
2
=0, 0158 J =0, 968 ·
2
m
l
(x
2
)=10x
2
v
1
=
r
r
T
3
− L
r
r
r
L
m
T
3
x
3
+
L
r
r
r
L
m
T
3
x
0
3
;
v
2
=
pm
l
J
+ µ(1 − 0, 5αx
2
1
− 0, 5βx
2
2
)x
2
− ω
2
x
1
.
v
1
v
2
ψ
1
=x
4
− v
1
;
ψ
2
=
3
2
p
2
L
m
JL
r
x
3
x
5
− v
2
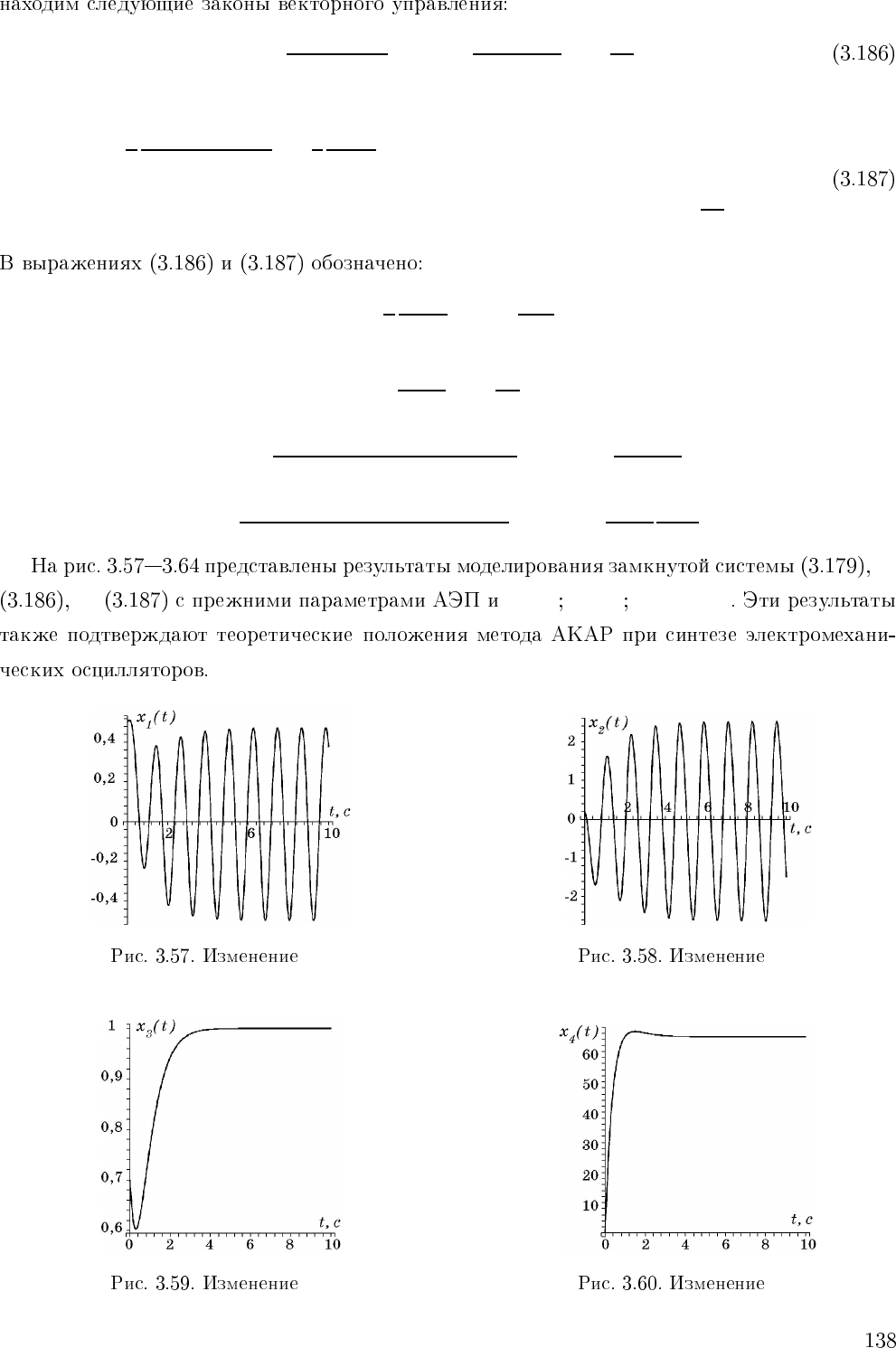
u
1
=
L
s
L
r
− L
2
m
L
r
−f
4
+
r
r
T
3
− L
r
r
r
L
m
T
3
f
3
−
ψ
1
T
1
,
u
2
=
2
3
J(L
s
L
r
− L
2
m
)
p
2
L
m
x
3
−
3
2
p
2
L
m
JL
r
(x
5
f
3
+ x
3
f
5
)+
+ µf
2
(1 − 0, 5αx
2
1
− 0, 5βx
2
2
) − µx
2
(αx
1
x
2
+ βx
2
f
2
) − ω
2
x
2
−
ψ
2
T
2
.
f
2
=
3
2
p
2
L
m
JL
r
x
3
x
5
−
pm
l
J
;
f
3
=
r
r
L
m
L
r
x
4
−
r
r
L
r
x
3
;
f
4
= −
(r
r
L
2
m
+ r
s
L
2
r
)x
4
+ r
r
L
m
x
3
L
r
(L
s
L
r
− L
2
m
)
+ x
2
x
5
+
r
r
L
m
x
2
5
L
r
x
3
;
f
5
=
(r
r
L
2
m
+ r
s
L
2
r
)x
5
+ L
r
L
m
x
2
x
3
L
r
(L
s
L
r
− L
2
m
)
+ x
2
x
4
+
r
r
L
m
L
r
x
4
x
5
x
3
.
u
1
u
2
µ =1 ω =5 α = β =1
x
1
x
2
x
3
x
4
x
5
u
1
u
2
X
2
X
3
X
4
˙
ψ
1
(t)=ψ
2
;
˙
ψ
2
(t)=(ε − ψ
2
1
)ψ
2
− ψ
1
,
ψ
1
= x
3
− x
0
3
=0;
ψ
2
= x
4
− x
0
4
=0.
u
1
=a
31
x
3
+ x
2
x
4
+
1
a
32
a
21
x
0
4
∂m
l
∂x
2
+
1
a
21
(ε
2
− x
2
1
)
(x
3
x
4
− m
l
)−
−
x
2
x
0
4
a
21
(2x
1
x
2
+1)+x
4
− x
0
4
;
u
2
=f
1
(x
4
)+
1
a
41
ε
1
−
x
3
−
1
x
0
4
m
l
+
1
a
21
ε
2
−x
2
1
x
2
−x
1
2
×
×
x
4
− x
0
4
− x
3
+
1
x
0
4
m
l
+
1
a
21
ε
2
− x
2
1
x
2
− x
1
.
