Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.


236 Lectures on Dynamics of Stochastic Systems
Thus, Eqs. (9.23) and (9.26) completely determine statistics of external forces,
and the nonlinear term in Eq. (9.22) plays no role for the one-time fluctuations of
v(t). Namely this feature constitutes the subject matter of the fluctuation – dissipation
theorem (the Callen–Welton theorem) in the context of HTS.
Note that Eqs. (9.22) with the correlation relationships (9.23) describe not only
equilibrium thermal fluctuations in HTS, but also the interaction of small-scale
motions (such as microturbulence, for example) with the motions of larger scales.
If such an HTS allows the description in terms of phenomenological equations (9.22)
with λ
(i)
= λ = const, σ
2
(i)
= σ
2
= const, the steady-state probability distribution of
v will have the form similar to distribution (9.25):
P(v) = C exp
−
λ
2σ
2
v
2
i
. (9.27)
Noises in Hydrodynamic-Type Systems Under the Regular Force
We illustrate statistical description of HTS by the example of the simplest system with
three degrees of freedom (S
3
), which is described by system of equations (1.23), page
14:
d
dt
v
0
(t) = v
2
2
(t) − v
2
1
(t) − v
0
(t) + R + f
0
(t),
d
dt
v
1
(t) = v
0
(t)v
1
(t) − v
1
(t) + f
1
(t),
d
dt
v
2
(t) = −v
0
(t)v
2
(t) − v
2
(t) + f
2
(t).
(9.28)
We assume that f
i
(t) are the Gaussian random forces delta-correlated in time with the
correlation tensor
f
i
(t)f
j
(t
0
)
= 2δ
ij
σ
2
δ(τ ).
In the absence of external forces, this system is equivalent to the Euler equations
of the dynamics of a gyroscope with isotropic friction, which is excited by a constant
moment of force relative to the unstable axis. The steady-state solution to this system
depends on parameter R (an analog to the Reynolds number), and the critical value of
this parameter is R
cr
= 1.
For R < 1, it has the stable steady-state solution
v
1 s-s
= v
s-s
= 0, v
0 s-s
= R. (9.29)
For R > 1, this solution becomes unstable with respect to small disturbances of
parameters, and new steady-state regime is formed:
v
0 s-s
= 1, v
2 s-s
= 0, v
1 s-s
= ±
√
R − 1. (9.30)
Methods for Solving and Analyzing the Fokker–Planck Equation 237
Here, we have an element of randomness because quantity v
1 s-s
can be either positive
or negative, depending on the amplitude of small disturbances.
As was mentioned earlier, the steady-state probability distribution at R = 0 has the
form
P(v) = C exp
(
−
v
2
i
2σ
2
)
. (9.31)
Assume now R 6= 0 and R < 1. In this case, we can easily obtain that fluctuations
of components relative to their steady-state values (ev
i
= v
i
− v
i s-s
) satisfy the system
of equations
d
dt
ev
0
(t) =ev
2
2
(t) −ev
2
1
(t) −ev
0
(t) + f
0
(t),
d
dt
ev
1
(t) =ev
0
(t)ev
1
(t) − (1 − R)ev
1
(t) + f
1
(t),
d
dt
ev
2
(t) = −ev
0
(t)ev
2
(t) − (1 + R)ev
2
(t) + f
2
(t).
(9.32)
Statistical characteristics of the solution to system (9.32) can be determined using
the perturbation theory with respect to small parameter σ
2
. The second moments of
componentsev
i
will then be described by the linearized system of equations (9.32); the
second moment being determined, mean values can be obtained by averaging system
(9.32) directly. The corresponding steady-state variances of fluctuations ev
i
have the
form
D
ev
2
0
(t)
E
= σ
2
,
D
ev
2
1
(t)
E
=
σ
2
1 − R
,
D
ev
2
2
(t)
E
=
σ
2
1 + R
. (9.33)
Note that expressions (9.33) hold for R 1. With increasing R, both intensity and
temporal correlation radius of component ev
1
increase, while the intensity of compo-
nent ev
2
decreases. In this process, maximum fluctuations of quantity ev
1
occur when
the dynamic system gets over the critical regime.
Consider now the case of R > 1. The steady-state probability distribution of com-
ponent v
1
has two maxima near v
1
= ±
√
R − 1 (they correspond to the stable steady-
state positions) and a minimum v
1
= 0 that corresponds to the unstable position. This
probability distribution is formed by ensemble averaging over realizations of random
forces f
i
(t). In a single realization, the system arrives with a probability of 1/2 at one of
the stable positions corresponding to distribution maxima. In this case, averaging over
time or ensemble averaging over the force realizations that bring the system to this
state will form the probability distribution near the maximum, and we can determine
statistical characteristics of the solution using the perturbation theory in parameter σ
2
.
Assume the system arrives at the state corresponding to the stable steady-state posi-
tion v
2 s-s
= 0, v
1 s-s
=
√
R − 1. Then, fluctuations relative to this state will satisfy the

238 Lectures on Dynamics of Stochastic Systems
system of equations
d
dt
ev
0
(t) =ev
2
2
(t) −ev
2
1
(t) − 2
√
R − 1ev
1
(t) −ev
0
(t) + f
0
(t),
d
dt
ev
1
(t) =ev
0
(t)ev
1
(t) +
√
R − 1ev
0
(t) + f
1
(t),
d
dt
ev
2
(t) = −ev
0
(t)ev
2
(t) − 2ev
2
(t) + f
2
(t).
(9.34)
For R 1, the second moments of fluctuations ev
i
are obtained from the linearized
system (9.34) and mean values are then determined by direct averaging of Eqs. (9.34).
Using this procedure, we obtain that, for R 1, the steady-state variances and corre-
lation coefficients of triplet components have the form
h
ev
0
(t)ev
2
(t)
i
=
h
ev
1
(t)ev
2
(t)
i
= 0,
h
ev
0
(t)ev
1
(t)
i
= −
σ
2
√
R
,
D
ev
2
0
(t)
E
= 3σ
2
,
D
ev
2
1
(t)
E
=
3
2
σ
2
,
D
ev
2
2
(t)
E
=
σ
2
2
.
(9.35)
As we mentioned earlier, these statistical characteristics correspond either to ave-
raging over time, or to ensemble averaging over realizations of forces f
i
(t) that bring
the system to the steady-state position. It should be noted that if the system has arrived
at one of the most probable states under the action of certain realization of forces f
i
(t),
it will be transferred into another most probable state after the lapse of certain time T
(the greater T, the greater R and the less σ
2
) in view of availability of sufficiently great
values of f
i
(t). This process simulated for a realization of random forces is shown in
Fig. 1.5 on page 14.
Consider now fluctuations of components v
i
(t) at critical regime (i.e., at R = 1).
Equations for the fluctuations relative to the state v
1 CT
= v
2 CT
= 0, v
0 CT
= R can be
obtained by setting R = 1 either in Eq. (9.32), or in Eq. (9.34). In this case, fluctuations
of componentev
2
(t) can be described in terms of the linearized equation (σ
2
1), and
the corresponding steady-state variance is given by the formula
D
ev
2
2
(t)
E
=
σ
2
2
.
Componentsev
0
(t) andev
1
(t) are described by the nonlinear system of equations
d
dt
ev
0
(t) = −ev
2
1
(t) −ev
0
(t) + f
0
(t),
d
dt
ev
1
(t) =ev
0
(t)ev
1
(t) + f
1
(t),
(9.36)
and no linearization is allowed here.
Methods for Solving and Analyzing the Fokker–Planck Equation 239
Averaging system (9.36), we obtain the following relationships for steady-state val-
ues of fluctuations
h
ev
0
(t)ev
1
(t)
i
= 0,
h
ev
0
(t)
i
= −
D
ev
2
1
(t)
E
.
As we noted earlier, intensity of fluctuationsev
1
increases in the critical regime and,
consequently, quantity
h
ev
0
(t)
i
increases. At the same time, the variance of fluctuation
ev
0
(t) remains nearly intact. Indeed, as follows from Eqs. (9.36), the variance of steady-
state fluctuationev
0
(t) is given by the formula
D
ev
2
0
(t)
E
= 2σ
2
.
It becomes clear that fluctuations ev
0
(t) andev
1
(t) can be estimated from the simplified
system
d
dt
ev
0
(t) = −ev
2
1
(t) −ev
0
(t) + f
0
(t),
d
dt
ev
1
(t) =
h
ev
0
(t)
i
ev
1
(t) + f
1
(t)
obtained by the replacement of quantity ev
0
(t) in the second equation of system (9.36)
by
h
ev
0
(t)
i
.
Using this system, we obtain that steady-state fluctuations ev
0
(t) and ev
1
(t) satisfy
the expressions
D
ev
2
1
(t)
E
= −
h
ev
0
(t)
i
= σ.
In a similar way, we obtain the estimate of the temporal correlation radius of quantity
ev
1
(t):
τ ∼ 1/σ.
Earlier, we considered the behavior of a triplet under the assumption that random
forces act on all variables. Let us see what will be changed if only one unstable compo-
nent v
0
(t) is affected by the random force (we assume that the force acting on compo-
nent v
0
(t) has regular (R) and random components). In this case, the dynamic system
assumes the form (R > 1)
d
dt
v
0
(t) = −v
2
1
(t) − v
0
(t) + R + f (t),
d
dt
v
1
(t) = v
0
(t)v
1
(t) − v
1
(t).
(9.37)
240 Lectures on Dynamics of Stochastic Systems
In system (9.37), we omitted the terms related to component v
2
(t), because one can
easily see that it will not be excited in the problem at hand.
Represent component v
0
(t) as v
0
(t) = 1 +ev
0
(t). The system of equations (9.37)
assumes then the form
d
dt
ev
0
(t) = −v
2
1
(t) −ev
0
(t) +
(
R − 1
)
+ f (t),
d
dt
v
1
(t) =ev
0
(t)v
1
(t),
(9.38)
from which follows that temporal evolution of component v
1
(t) depends on its initial
value.
If v
1
(0) > 0, then v
1
(t) > 0 too. In this case, we can represent v
1
(t) in the form
v
1
(t) = e
ϕ(t)
and rewrite the system of equations (9.38) in the Hamiltonian form (9.19)
d
dt
ev
0
(t) = −
∂U(ϕ)
∂ϕ
−ev
0
(t) + f (t),
d
dt
ϕ(t) =ev
0
(t), (9.39)
where
U(ϕ) =
1
2
e
2ϕ
−
(
R − 1
)
ϕ.
Here, variable ϕ(t) plays the role of particle’s coordinate and variable v
0
(t) plays the
role of particle’s velocity.
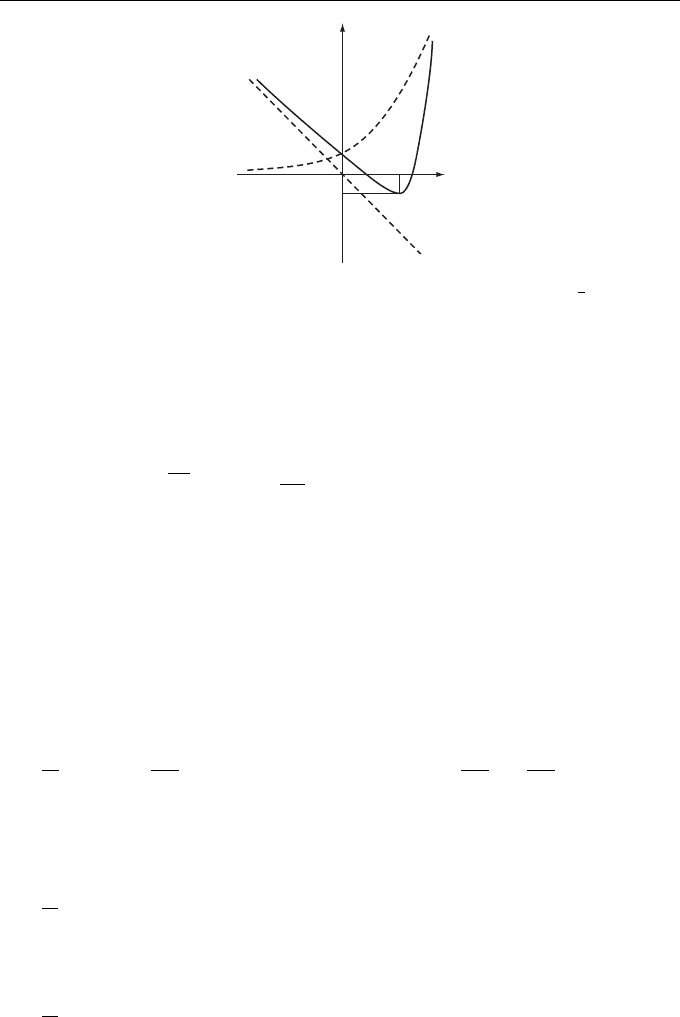
The solid line in Fig. 9.1 shows the behavior of function U(ϕ). At point ϕ
0
=
ln
√
R − 1, this function has a minimum
U(ϕ
0
) =
1
2
(R − 1)
[
1 − ln(R −1)
]
corresponding to the stable equilibrium state v
1
=
√
R − 1. Thus, the steady-state
probability distribution of ϕ(t) and ev
0
(t) is similar to the Gibbs distribution (9.20)
P(ev
0
, ϕ) = C exp
−
1
D
H(ev
0
, ϕ)
, H(ev
0
, ϕ) =
ev
2
0
2
+ U(ϕ). (9.40)
From Eq. (9.40) follows that, for R > 1, the steady-state probability distribution is
composed of two independent steady-state distributions, of which the distribution of
component v
0
(t) of system (9.37) is the Gaussian distribution
P(v
0
) =
1
√
2πD
exp
−
(v
0
− 1)
2
2D
, (9.41)
Methods for Solving and Analyzing the Fokker–Planck Equation 241
ϕ
ϕ
0
U (ϕ
0
)
U (ϕ)
Figure 9.1 Potential function U(ϕ). The dashed lines show curve U(ϕ) =
1
2
exp{2ϕ} and
straight line U(ϕ) = −(R −1)ϕ.
and the distribution of quantity ϕ(t) is the non-Gaussian distribution. If we turn back
to variable v
1
(t), we obtain the corresponding steady-state probability distribution in
the form
P(v
1
) = const v
R−1
D
−1
1
exp
(
−
v
2
1
2D
)
. (9.42)
As may be seen from Eq. (9.42), no steady-state probability distribution exists for
component v
1
(t) in critical regime(R = 1), which contrasts with the above case when
random forces acted on all components of the triplet.
Earlier, we mentioned that two stages are characteristic of the formation of distri-
bution (9.40). First, the Maxwellian distribution with respect to v
0
(9.41) is rapidly
formed and the distribution with respect to ϕ is then formed at a much slower rate.
The second stage is described by the Einstein–Smolukhovsky equation (9.17) that, in
terms of variable v
1
, assumes the form
∂
∂t
P(v
1
, t) =
∂
∂v
1
n
v
1
h
v
2
1
− (R − 1)
i
P(v
1
, t)
o
+ σ
2
∂
∂v
1
v
1
∂
∂v
1
[
v
1
P(v
1
, t)
]
.
(9.43)
This equation is the Fokker–Planck equation for the stochastic dynamic equation
d
dt
v
1
(t) = −v
1
(t)
h
v
2
1
(t) − (R − 1)
i
+ v
1
(t)f (t).
At critical regime R = 1, this equation assumes the form
d
dt
v
1
(t) = −v
3
1
(t) + v
1
(t)f (t),
from which follows that, despite strong nonlinear friction, its solution is stochastically
unstable due to the specific form of the random term. Stochastic stabilization occurs,
242 Lectures on Dynamics of Stochastic Systems
as we saw earlier, due to inclusion of random forces into the equations for other com-
ponents.
9.3 Boundary-Value Problems for the Fokker–Planck
Equation (Hopping Phenomenon)
The Fokker–Planck equations are the partial differential equations and they generally
require boundary conditions whose particular form depends on the problem under con-
sideration. One can proceed from both forward and backward Fokker–Planck equa-
tions, which are equivalent. Consider one typical example.
Consider the nonlinear oscillator with friction described by the equation
d
2
dt
2
x(t) + λ
d
dt
x(t) + ω
2
0
x(t) + βx
3
(t) = f (t) (β, λ > 0) (9.44)
and assume that random force f (t) is the delta-correlated random function with the
parameters
h
f (t)
i
= 0,
f (t)f (t
0
)
= 2Dδ(t − t
0
) (D = σ
2
f
τ
0
).
At λ = 0 and f (t) = 0, this equation is called the Duffing equation.
We can rewrite Eq. (9.44) in the standard form of the Hamiltonian system in func-
tions x(t) and v(t) =
d
dt
x(t),
d
dt
x(t) =
∂
∂v
H(x, v),
d
dt
v(t) = −
∂
∂x
H(x, v) − λv + f (t),
where
H(x, v) =
v
2
2
+ U(x), U(x) =
ω
2
0
x
2
2
+ β
x
4
4
is the Hamiltonian.
According to Eq. (9.20), the steady-state solution to the corresponding Fokker–
Planck equation has the form
P(x, v) = C exp
−
λ
D
H(x, v)
. (9.45)
It is clear that this distribution is the product of two independent distributions, of
which one – the steady-state probability distribution of quantity v(t) – is the Gaussian
distribution and the other – the steady-state probability distribution of quantity x(t) – is

Methods for Solving and Analyzing the Fokker–Planck Equation 243
the non-Gaussian distribution. Integrating Eq. (9.45) over v, we obtain the steady-state
probability distribution of x(t)
P(x) = C exp
(
−
λ
D
ω
2
0
x
2
2
+ β
x
4
4
!)
.
This distribution is maximum at the stable equilibrium point x = 0.
Consider now the equation
d
2
dt
2
x(t) + λ
d
dt
x(t) − ω
2
0
x(t) + βx
3
(t) = f (t) (β, λ > 0). (9.46)
In this case again, the steady-state probability distribution has the form (9.45), where
now
H(x, v) =
v
2
2
+ U(x), U(x) = −
ω
2
0
x
2
2
+ β
x
4
4
.
The steady-state probability distribution of x(t) assumes now the form
P(x) = C exp
(
−
λ
D
−
ω
2
0
x
2
2
+ β
x
4
4
!)
(9.47)
and has maxima at points x = ±
q
ω
2
0
/β and a minimum at point x = 0; the max-
ima correspond to the stable equilibrium points of problem (9.46) for f (t) = 0 and
the minimum, to the instable equilibrium point. Figure 9.2 shows the behavior of the
probability distribution (9.47).
As we mentioned earlier, the formation of distribution (9.47) is described by the
Einstein–Smolukhovsky equation (9.17), which has in this case the form
∂
∂t
P(x, t) =
1
λ
∂
∂x
∂U(x)
∂x
P(x, t)
+
1
λ
2
∂
2
∂x
2
P(x, t). (9.48)
This equation is statistically equivalent to the dynamic equation
d
dt
x(t) = −
1
λ
∂U(x)
∂x
+
1
λ
f (t). (9.49)
x
P (x )
ω
2
0
/β
−
√
ω
2
0
/β
√
Figure 9.2 Probability distribution (9.47).

244 Lectures on Dynamics of Stochastic Systems
Probability distribution (9.47) corresponds to averaging over an ensemble of real-
izations of random process f (t). If we deal with a single realization, the system arrives
at one of states corresponding to the distribution maxima with a probability of 1/2. In
this case, averaging over time will form the probability distribution around the max-
imum position. However, after a lapse of certain time T (the longer, the smaller D),
the system will be transferred in the vicinity of the other maximum due to the fact that
function f (t) can assume sufficiently large values. For this reason, temporal averaging
will form probability distribution (9.48) only if averaging time t T.
Introducing dimensionless coordinate x →
s
ω
2
0
β
x and time t →
λ
ω
2
0
t, we can
rewrite Eq. (9.48) in the form
∂
∂t
P(x, t) =
∂
∂x
∂U(x)
∂x
P(x, t)
+ µ
∂
2
∂x
2
P(x, t), (9.50)
where
µ =
βD
λω
4
0
, U(x) = −
x
2
2
+
x
4
4
.
In this case, the equivalent stochastic equation (9.49) assumes the form of Eq. (1.15),
page 10
d
dt
x(t) = −
∂U(x)
∂x
+ f (t). (9.51)
Estimate the time required for the system to switch from a most probable state
x = −1 to the other x = 1.
Assume the system described by stochastic equation (9.51) was at a point from the
interval (a, b) at instant t
0
. The corresponding probability for the system to leave this
interval
G(t;x
0
, t
0
) = 1 −
b
Z
a
dxp(x, t|x
0
, t
0
)
satisfies Eq. (8.21) following from the backward Fokker–Planck equation (8.20),
page 196, i.e., the equation
∂
∂t
0
G(t;x
0
, t
0
) =
∂U(x
0
)
∂x
0
∂
∂x
0
G(t;x
0
, t
0
) − µ
∂
2
∂x
2
0
G(t;x
0
, t
0
)
with the boundary conditions
G(t;x
0
, t) = 0, G(t;a, t
0
) = G(t;b, t
0
) = 1.

Methods for Solving and Analyzing the Fokker–Planck Equation 245
Taking into account the fact that G(t;x
0
, t
0
) = G(t − t
0
;x
0
) in our problem, we can
denote (t − t
0
) = τ and rewrite the boundary-value problem in the form
∂
∂τ
G(τ ;x
0
) =
∂U(x
0
)
∂x
0
∂
∂x
0
G(τ ;x
0
) − µ
∂
2
∂x
2
0
G(τ ;x
0
),
G(0;x
0
) = 0, G(τ ;a, ) = G(τ ;b) = 1
lim
τ →∞
G(τ ;x
0
) = 0
.
(9.52)
From Eq. (9.52), one can easily see that average time required for the system to
leave interval (a, b)
T(x
0
) =
∞
Z
0
dτ τ
∂G(τ ;x
0
)
∂τ
satisfies the boundary-value problem
µ
d
2
T(x
0
)
dx
2
0
−
dU(x
0
)
dx
0
dT(x
0
)
dx
0
= −1, T(a) = T(b) = 0. (9.53)
Equation (9.53) can be easily solved, and we obtain that the average time required
for the system under random force to switch its state from x
0
= −1 to x
0
= 1 (this
time is usually called the Kramers time) is given by the expression
T =
1
µ
1
Z
−1
dξ
ξ
Z
−∞
dη exp
1
µ
[
U(ξ ) − U(η)
]
=
C(µ)
µ
1
Z
0
dξ exp
1
µ
U(ξ )
,
(9.54)
where C(µ) =
∞
Z
−∞
dξ exp
1
µ
U(ξ )
. For µ 1, we obtain
T ≈
√
2π exp
1
4µ
,
i.e., the average switching time increases exponentially with decreasing the intensity
of fluctuations of the force.
9.4 Method of Fast Oscillation Averaging
If fluctuations of dynamic system parameters are sufficiently small, we can analyze
the Fokker–Planck equation using different asymptotic and approximate techniques.
