Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.


206 Lectures on Dynamics of Stochastic Systems
are distributed according to the steady-state probability density
P(S
n
;α) =
1
n
2
D
α/nD
0
α
D
S
1+α/D
n
exp
−
1
n
2
DS
n
,
where 0(z) is the gamma function. In the special case n = 1, quantity
S(α) = S
1
(α) =
∞
Z
0
dτ y(τ ;α)
has the following probability density
P(S;α) =
1
D
α/D
0
α
D
S
1+α/D
exp
−
1
DS
. (8.50)
If we set now α =D, then the steady-state probability density and the corresponding integ-
ral distribution function will have the form
P(S;D) =
1
DS
2
exp
−
1
DS
, F(S;D) = exp
−
1
DS
. (8.51)
The time-dependent behavior of the probability density of random process
e
S(t, α) =
∞
Z
t
dτ y(τ ;α) (8.52)
gives an additional information about the behavior of realizations of process y(t;α) with
time t. The integral in the right-hand side of Eq. (8.52) can be represented in the form
e
S(t, α) = y(t;α)
∞
Z
0
dτ exp
−ατ +
τ
Z
0
dτ
1
z(τ
1
+ t)
. (8.53)
In Eq. (8.53), random process y(t;α) is statistically independent of the integral factor,
because they depend functionally on process z(τ ) for nonoverlapping intervals of times
τ ; in addition, the integral factor by itself appears statistically equivalent to random quan-
tity S(α). Consequently, the one-time probability density P(
e
S, t;α) =
δ
e
S(t;α) −
e
S
of
random process
e
S(t, α) is described by the expression
P(
e
S, t;α) =
∞
Z
0
∞
Z
0
dydSδ(yS −
e
S)P(y, t;α) =
∞
Z
0
dy
y
P(y, t;α)P
e
S
y
;α
, (8.54)
where P(y, t;α) is the one-time probability density of lognormal process y(t;α) (8.33) and
P
e
S
y
;α
is the probability density (8.50) of random area.

Approximations of Gaussian Random Field Delta-Correlated in Time 207
The corresponding integral distribution function
F(
e
S, t;α) = P
e
S(t;α) <
e
S
=
e
S
Z
0
d
e
SP(
e
S, t;α)
is given by the integral
F(
e
S, t;α) =
∞
Z
0
dyP(y, t;α)F
e
S
y
;α
,
where F(S;α) is the integral distribution function of random area S(t;α). In the special
case α = D, we obtain, according to Eq. (8.33) and (8.51), the expression
F(
e
S, t;D) =
1
2
√
πDt
∞
Z
0
dy
y
exp
(
−
ln
2
ye
Dt
4Dt
−
y
D
e
S
)
from which follows that the probability of the event that inequality
e
S(t;D) <
e
S is satisfied
monotonously tends to unity with increasing Dt for any predetermined value of D
e
S. This is
an additional evidence in favor of the fact that every separate realization of the lognormal
process tends to zero with increasing Dt, though moment functions of process y(t;α) show
the exponential growth caused by large spikes.
(5) Now, we dwell on positive random fields E(r, t) closely related to lognormal processes
whose one-point probability density is described by the equation
∂
∂t
− D
0
∂
2
∂r
2
!
P(r, t;E) =
α
∂
∂E
E + D
∂
∂E
E
∂
∂E
E
P(r, t;E),
P(r, 0;E) = δ
(
E − E
0
(r)
)
,
(8.55)
where D
0
is the coefficient of diffusion in r-space, and coefficients α and D characterize
diffusion in E-space. Parameter α can be both positive and negative. In the context of the
one-point characteristics, the change of sign of parameter α means transition from random
field E(r, t) to random field
e
E(r, t) = 1/E(r, t). For definiteness, we will term field E(r, t)
energy.
The solution to this equation has the form
P(r, t;E) = exp
(
D
0
t
∂
2
∂r
2
)
e
P(r, t;E),
where function
e
P(r, t;E) satisfies the equation (cf. with Eq. (8.36))
∂
∂t
e
P(r, t;E) =
α
∂
∂E
E + D
∂
∂E
E
∂
∂E
E
e
P(r, t;E),
e
P(r, 0;E) = δ
(
E − E
0
(r)
)
.
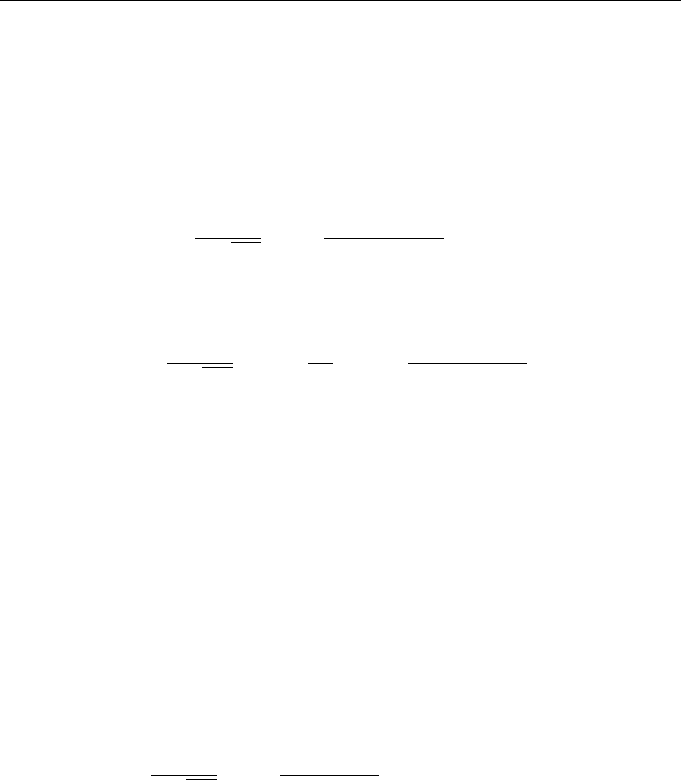
208 Lectures on Dynamics of Stochastic Systems
As may be seen, dependence of function
e
P(r, t;E) on parameter r is determined solely by
initial value E
0
(r), i.e.,
e
P(r, t;E) ≡
e
P(t;E|E
0
(r))
and, hence, function
e
P(t;E|E
0
(r)) is the lognormal probability density of random process
E(t, |E
0
(r)) dependent on r parametrically,
e
P(t;E|E
0
(r)) =
1
2E
√
πDt
exp
(
−
ln
2
Ee
αt
/E
0
(r)
4Dt
)
.
Thus, the solution to Eq. (8.55) has the form
P(r, t;E) =
1
2E
√
πDt
exp
(
D
0
t
∂
2
∂r
2
)
exp
(
−
ln
2
Ee
αt
/E
0
(r)
4Dt
)
. (8.56)
A consequence of equation (8.55) or expression (8.56) are relationships for spatial inte-
grals of moment functions (for all n > 0 and n < 0)
Z
dr
E
n
(r, t)
= e
n(nD−α)t
Z
drE
n
0
(r),
which are independent of the coefficient of diffusion in r-space (coefficient D
0
), and, in
particular, the expression for average total energy in the whole space,
Z
dr
h
E(r, t)
i
= e
γ t
Z
drE
0
(r),
where γ = D−α. If the initial energy distribution is homogeneous, E
0
(r) = E
0
, probability
density (8.56) is independent of r and is given by Eq. (8.33),
P(t;E) =
1
2E
√
πDt
exp
(
−
ln
2
Ee
αt
/E
0
4Dt
)
. (8.57)
Thus, in this case, the one-point statistical characteristics of energy E(r, t) are statis-
tically equivalent to statistical characteristics of random process E(t) = y(t;α) (8.32). A
characteristic feature of distribution (8.57) consists in a long flat tail appeared for Dt 1,
which is indicative of an increased role of great peaks of process E(t;α) in the forma-
tion of the one-point statistics. For this distribution, all moments of energy are exponential
functions and, in particular,
h
E(t)
i
= E
0
e
γ t
, γ = D − α
at n = 1, and
h
ln
(
E(t)/E
0
)
i
= −αt,
Approximations of Gaussian Random Field Delta-Correlated in Time 209
so that the typical realization curve determining the behavior of energy at arbitrary spatial
point in specific realizations of random process E(t) is the exponential quantity
E
∗
(t) = E
0
e
−αt
increasing or decreasing with time. For α < 0, the typical realization curve exponentially
increases with time, which is evidence of general increase of energy at every spatial point.
Otherwise, for α > 0, the typical realization curve exponentially decreases at every spatial
point, which is indicative of cluster structure of energy field.
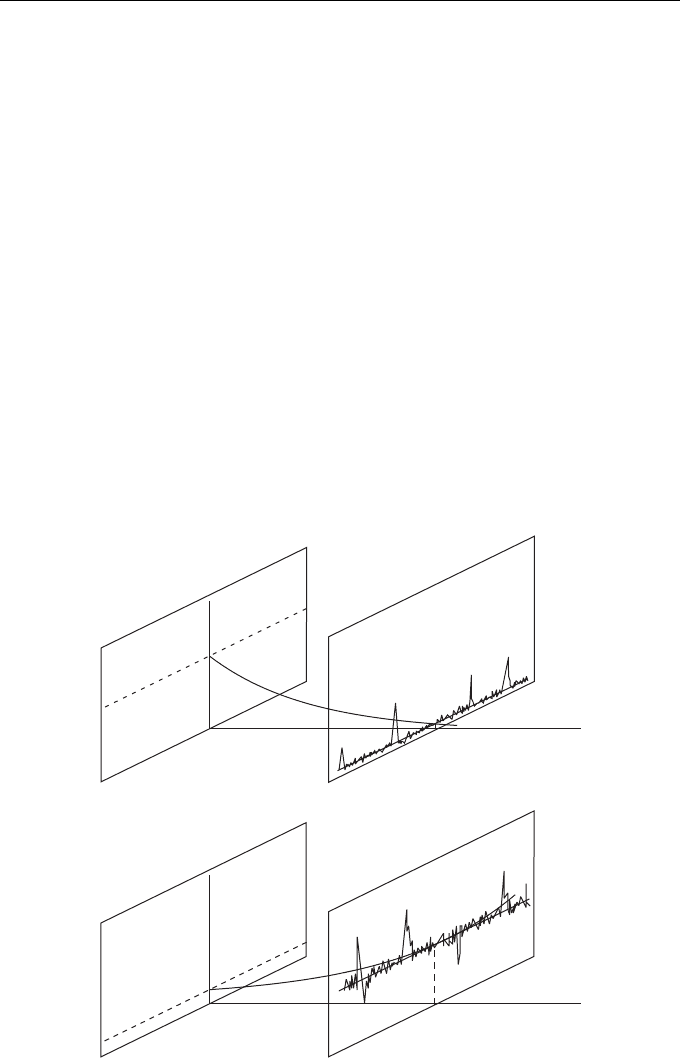
Figure 8.4 schematically shows random realizations of energy field for different signs
of parameter α.
The knowledge of the one-point probability density of energy (8.56) yields general
knowledge of the spatial structure of energy. In particular, functionals of the energy
field such as total average volume (in the three-dimensional case) or area (in the two-
dimensional case) of the region in which E(r, t) > E and total average energy contained in
this region are given by the equalities
h
V(t, E)
i
=
∞
Z
E
d
e
E
Z
dr P(r, t;
e
E),
h
E(t, E)
i
=
∞
Z
E
e
Ed
e
E
Z
dr P(r, t;
e
E).
r
r
t
α > 0
1
E
∗
(t )
t
1
E (r, 0)
E (r, t
1
)
E (r, 0)
r
r
t
t
1
1
α < 0
E (r, t
1
)
E
∗
(t )
Figure 8.4 Schematic behavior of random realization of energy for α > 0 and α < 0.
210 Lectures on Dynamics of Stochastic Systems
The values of these functionals are independent of the coefficient of diffusion in
r-space (coefficient D
0
), and, using probability density (8.56), we obtain the expressions
h
V(t, E)
i
=
Z
dr Pr
1
√
2Dt
ln
E
0
(r)
E
e
−αt
,
h
E(t, E)
i
= e
γ t
Z
dr E
0
(r) Pr
1
√
2Dt
ln
E
0
(r)
E
e
(
2D−α
)
t
,
(8.58)
where probability integral Pr(z) is defined by Eq. (4.20), page 94. Asymptotic expressions
of function Pr(z) for z → ∞ and z → −∞ (4.23), page 95, offer a possibility of studying
temporal evolution of these functionals. Namely, average volume asymptotically decays
(for α > 0) with time (t → ∞) according to the law
h
V(t, E)
i
≈
1
α
r
D
πE
α/D
t
e
−α
2
t/4D
Z
dr
q
E
α/D
0
(r).
On the contrary, for α < 0, average volume occupies the whole space for t → ∞.
Asymptotic behavior of total energy for t → ∞ has the form (in the most interesting
case of γ > 0, α < D)
h
E(t, E)
i
≈ e
γ t
Z
drE
0
(r)
1 −
1
(
2D −α
)
s
D
πt
E
E
0
(r)
(2D−α)/D
e
−
(
2D−α
)
2
t/4
,
which means that 100% of total average energy is contained in clusters for α > 0.
In the case of homogeneous initial conditions, the corresponding expressions without
integration over r present specific values of volume occupied by large peaks and their total
energy per unit volume:
h
V(t, E)
i
= Pr
1
√
2Dt
ln
E
0
(r)
E
e
−αt
,
h
E(t, E)
i
= E
0
e
γ t
Pr
1
√
2Dt
ln
E
0
(r)
E
e
(
2D−α
)
t
,
(8.59)
where γ = D − α.
If we take section at level E > E
0
, then the initial values of these quantities will be equal
to zero at the initial instant,
h
V(0, E)
i
= 0 and
h
E(0, E)
i
= 0. Then, spatial disturbances of
energy field appear with time and, for t → ∞, they are given by the following asymptotic
expressions:
h
V(t, E)
i
≈
1
α
s
D
πt
E
0
E
α/D
e
−α
2
t/4D
(α > 0),
1 −
1
|α|
s
D
πt
E
E
0
|α|/D
e
−α
2
t/4D
(α < 0),

Approximations of Gaussian Random Field Delta-Correlated in Time 211
and, for D > α,
h
E(t, E))
i
≈ E
0
e
γ t
1 −
1
(
2D −α
)
s
D
πt
E
E
0
(2D−α)/D
e
−(2D−α)
2
t/4D
.
Thus, for α > 0, specific total volume tends to zero and specific total energy increases
with time as average energy does, which is evidence of clustering the field of energy in
this case.
For α < 0, no clustering occurs and specific volume occupies the whole space in which
specific energy increases with time as average energy does.
8.4 Applicability Range of the Fokker–Planck Equation
To estimate the applicability range of the Fokker–Planck equation, we must include
into consideration the finite-valued correlation radius τ
0
of field f(x, t) with respect to
time. Thus, smallness of parameter τ
0
/T is the necessary but generally not sufficient
condition in order that one can describe the statistical characteristics of the solution
to Eq. (8.1), using the approximation of the delta-correlated random field of which a
consequence is the Fokker–Planck equation. Every particular problem requires more
detailed investigation. Below, we give a more physical method called the diffusion
approximation. This method also leads to the Markovian property of the solution to
Eq. (8.1); however, it considers to some extent the finite value of the temporal corre-
lation radius.
Here, we emphasize that the approximation of the delta-correlated random field
does not reduce to the formal replacement of random field f (x, t) in Eq. (8.1) with
the random field with correlation function (8.4). This approximation corresponds to
the construction of an asymptotic expansion in temporal correlation radius τ
0
of filed
f (x, t) for τ
0
→ 0. It is in such a limited process that exact average quantities like
f (x, t)R[t;f (x
0
, τ )]
grade into the expressions obtained by the formal replacement of the correlation tensor
of field f(x, t) with the effective tensor (8.4).
8.4.1 Langevin Equation
We illustrate the above speculation with the example of the Langevin equation that
allows an exhaustive statistical analysis. This equation has the form
d
dt
x(t) = −λx(t) + f (t), x(t
0
) = 0 (8.60)
and assumes that the sufficiently fine smooth function f (t) is the stationary Gaussian
process with zero-valued mean and correlation function
f (t)f (t
0
)
= B
f
(t − t
0
).

212 Lectures on Dynamics of Stochastic Systems
For any individual realization of random force f (t), the solution to Eq. (8.60) has
the form
x(t) =
t
Z
t
0
dτ f (τ)e
−λ(t−τ )
.
Consequently, this solution x(t) is also the Gaussian process with the parameters
h
x(t)
i
= 0,
x(t)x(t
0
)
=
t
Z
t
0
dτ
1
t
0
Z
t
0
dτ
2
B
f
(τ
1
− τ
2
)e
−λ(t+t
0
−τ
1
−τ
2
)
.
In addition, we have, for example,
h
f (t)x(t)
i
=
t−t
0
Z
0
dτ B
f
(τ )e
−λτ
.
Note that the one-point probability density P(x, t) =
h
δ(x(t) − x)
i
for Eq. (8.60)
satisfies the equation
∂
∂t
− λ
∂
∂x
x
P(x, t) =
t−t
0
Z
0
dτ B
f
(τ )e
−λτ
∂
2
∂x
2
P(x, t), P(x, t
0
) = δ(x),
which rigorously follows from Eq. (6.24), page 149. As a consequence, we obtain
d
dt
x
2
(t)
= −2λ
x
2
(t)
+ 2
t−t
0
Z
0
dτ B
f
(τ )e
−λτ
.
For t
0
→ −∞, process x(t) grades into the stationary Gaussian process with the
following one-time statistical parameters (
h
x(t)
i
= 0)
σ
2
x
=
x
2
(t)
=
1
λ
∞
Z
0
dτ B
f
(τ )e
−λτ
,
f (t)x(t)
=
∞
Z
0
dτ B
f
(τ )e
−λτ
.
In particular, for exponential correlation function B
f
(t),
B
f
(t) = σ
2
f
e
−|τ |/τ
0
,
we obtain the expressions
h
x(t)
i
= 0,
D
x
2
(t)
E
=
σ
2
f
τ
0
λ(1 + λτ
0
)
,
h
f (t)x(t)
i
=
σ
2
f
τ
0
1 + λτ
0
, (8.61)

Approximations of Gaussian Random Field Delta-Correlated in Time 213
which grade into the asymptotic expressions
x
2
(t)
=
σ
2
f
τ
0
λ
,
h
f (t)x(t)
i
= σ
2
f
τ
0
(8.62)
for τ
0
→ 0.
Multiply now Eq. (8.60) by x(t). Assuming that function x(t) is sufficiently fine
function, we obtain the equality
x(t)
d
dt
x(t) =
1
2
d
dt
x
2
(t) = −λx
2
(t) + f (t)x(t).
Averaging this equation over an ensemble of realizations of function f (t), we obtain
the equation
1
2
d
dt
x
2
(t)
= −λ
x
2
(t)
+
f (t)x(t)
, (8.63)
whose steady-state solution (it corresponds to the limit process t
0
→ −∞and τ
0
→ 0)
x
2
(t)
=
1
λ
f (t)x(t)
coincides with Eq. (8.61) and (8.62).
Taking into account the fact that δx(t)/δf (t − 0) = 1, we obtain the same result for
correlation
h
f (t)x(t)
i
by using the formula
h
f (t)x(t)
i
=
t
Z
−∞
dτ B
f
(t − τ )
δ
δf (τ)
x(t)
(8.64)
with the effective correlation function
B
eff
f
(t) = 2σ
2
f
τ
0
δ(t).
Earlier, we mentioned that statistical characteristics of solutions to dynamic prob-
lems in the approximation of the delta-correlated random process (field) coincide with
the statistical characteristics of the Markovian processes. However, one should clearly
understand that this is the case only for statistical averages and equations for these ave-
rages. In particular, realizations of process x(t) satisfying the Langevin equation (8.60)
drastically differ from realizations of the corresponding Markovian process. The lat-
ter satisfies Eq. (8.60) in which function f (t) in the right-hand side is the ideal white
noise with the correlation function B
f
(t) = 2σ
2
f
τ
0
δ(t); moreover, this equation must
be treated in the sense of generalized functions, because the Markovian processes
are not differentiable in the ordinary sense. At the same time, process x(t) – whose

214 Lectures on Dynamics of Stochastic Systems
statistical characteristics coincide with the characteristics of the Markovian process –
behaves as a sufficiently fine function and is differentiable in the ordinary sense. For
example,
x(t)
d
dt
x(t) =
1
2
d
dt
x
2
(t),
and we have for t
0
→ −∞ in particular
x(t)
d
dt
x(t)
= 0. (8.65)
On the other hand, in the case of the ideal Markovian process x(t) satisfying (in the
sense of generalized functions) the Langevin equation (8.60) with the white noise
in the right-hand side, Eq. (8.65) makes no sense at all, and the meaning of the
relationship
x(t)
d
dt
x(t)
= −λ
D
x
2
(t)
E
+
h
f (t)x(t)
i
(8.66)
depends on the definition of averages. Indeed, if we will treat Eq. (8.66) as the limit
of the equality
x(t + 1)
d
dt
x(t)
= −λ
h
x(t)x(t + 1)
i
+
h
f (t)x(t + 1)
i
(8.67)
for 1 → 0, the result will be essentially different depending on whether we use limit
processes 1 → +0, or 1 → −0. For limit process 1 → +0, we have
lim
1→+0
h
f (t)x(t + 1)
i
= 2σ
2
f
τ
0
,
and, taking into account Eq. (8.64), we can rewrite Eq. (8.67) in the form
x(t + 0)
d
dt
x(t)
= σ
2
f
τ
0
. (8.68)
On the contrary, for limit process 1 → −0, we have
h
f (t)x(t − 0)
i
= 0
because of the dynamic causality condition, and Eq. (8.67) assumes the form
x(t − 0)
d
dt
x(t)
= −σ
2
f
τ
0
. (8.69)

Approximations of Gaussian Random Field Delta-Correlated in Time 215
Comparing Eq. (8.65) with Eq. (8.68) and (8.69), we see that, for the ideal Markovian
process described by the solution to the Langevin equation with the white noise in the
right-hand side and commonly called the Ohrnstein–Ulenbeck process, we have
x(t + 0)
d
dt
x(t)
6=
x(t − 0)
d
dt
x(t)
6=
1
2
d
dt
D
x
2
(t)
E
.
Note that equalities (8.68) and (8.69) can also be obtained from the correlation
function
h
x(t)x(t + τ )
i
=
σ
2
f
τ
0
λ
e
−λ|τ |
of process x(t).
To conclude with a discussion of the approximation of the delta-correlated random
process (field), we emphasize that, in all further examples, we will treat the statement
‘dynamic system (equation) with the delta-correlated parameter fluctuations’ as the
asymptotic limit in which these parameters have temporal correlation radii small in
comparison with all characteristic temporal scales of the problem under consideration.
8.5 Causal Integral Equations
In problems discussed earlier, we succeeded in deriving the closed statistical descrip-
tion in the approximation of the delta-correlated random field due to the fact that each
of these problems corresponded to a system of the first-order (in temporal coordinate)
differential equations with given initial conditions at t = 0. Such systems possess the
dynamic causality property, which means that the solution at instant t depends only on
system parameter fluctuations for preceding times and is independent of fluctuations
for consequent times.
However, problems described in terms of integral equations that generally cannot
be reduced to a system of differential equations can also possess the causality property.
In short, we illustrate this fact by the simplest example of the one-dimensional causal
equation (t > t
0
)
G(t;t
0
) = g(t;t
0
) + 3
t
Z
t
0
dτ g(t;τ )z(τ )G(τ ;t
0
), (8.70)
where function g(t;t
0
) is Green’s function for the problem with absent parameter fluc-
tuations, i.e., for z(t) = 0, and we assume that z(t) is the Gaussian delta-correlated
random function with the parameters
h
z(t)
i
= 0,
z(t)z(t
0
)
= 2Dδ(t − t
0
) (D = σ
2
z
τ
0
).
