Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.

226 Lectures on Dynamics of Stochastic Systems
0
4
8
E
(a)
E
(b)
0
0.5
1
6
10
15 20
0
0.01
0.02
0.03
P(t ; E )
P(t ; E )
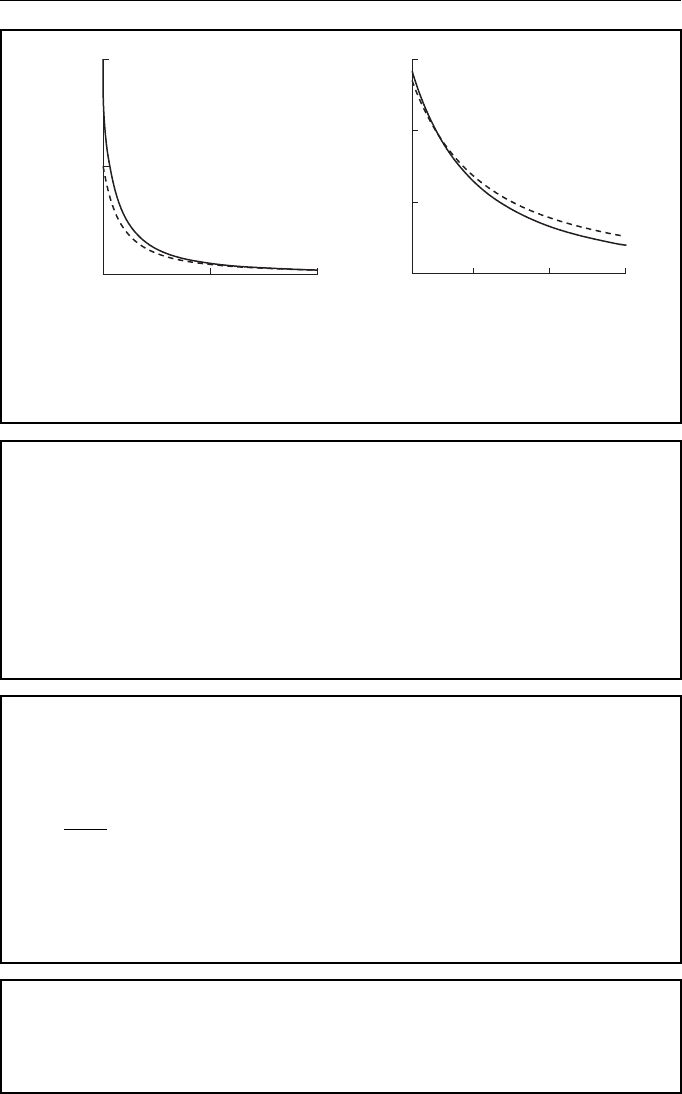
Figure 8.6 Probability distributions at β = 0 at time t = 10 for energy in intervals (a)
(0, 8) and (b) (6, 20).
Problem 8.7
Find the relationship between fields q(r, t) and p(r, t) whose moment functions
are given by the expressions
q
n
(r, t)
= exp
{
n(n + 0, 5)t
}
,
p
n
(r, t)
= exp
{
n(n − 0, 5)t
}
.
Which field possesses the property of clustering?
Solution q(r, t) = 1/p(r, t) and clustering occurs for field p(r, t).
Problem 8.8
Show that integral equation (8.70) is equivalent to the variational derivative
equation
δ
δz(τ )
G(t, t
0
) = G(t, τ )3G(τ, t
0
) (t
0
≤ τ ≤ t)
with the initial condition
G(t, t
0
)
z(τ )=0
= g(t, t
0
).
Problem 8.9
Construct the diffusion approximation for the problem on the dynamics of a
particle with linear friction under random forces, which is described by the
Approximations of Gaussian Random Field Delta-Correlated in Time 227
stochastic system (1.12), page 8,
d
dt
r(t) = v(t),
d
dt
v(t) = −λv(t) + f (r, t),
r(0) = r
0
, v(0) = v
0
.
Solution The one-time probability density of particle position and velocity
P(r, v, t) =
h
δ(r(t) − r)δ(v(t) − v)
i
satisfies the Fokker–Planck equation
∂
∂t
+ v
∂
∂r
− λ
∂
∂v
v
P(r, v, t) =
∂
∂v
i
D
(1)
ij
(v)
∂
∂v
j
+ D
(2)
ij
(v)
∂
∂r
j
P(r, v, t).
(8.93)
with the diffusion coefficients
D
(1)
ij
(v) =
∞
Z
0
dτ e
−λτ
B
ij
1
λ
e
λτ
− 1
v, τ
,
D
(2)
ij
(v) =
1
λ
∞
Z
0
dτ
1 − e
−λτ
B
ij
1
λ
e
λτ
− 1
v, τ
.
(8.94)
Problem 8.10
In the diffusion approximation, find the steady-state probability distribution of
the velocity of a particle described by dynamic system (1.12), page 8, in the one-
dimensional case assuming that the force correlation function has the form
B
f
(x, t) = σ
2
f
exp
−
|x|
l
0
−
|t|
τ
0
.
Solution From Eq. (8.93) follows that steady-state probability density of par-
ticle’s velocity (i.e., probability density in limit t → ∞) satisfies the equation
−λvP(v) = D(v)
∂
∂v
P(v), (8.95)

228 Lectures on Dynamics of Stochastic Systems
where, in accordance with Eq. (8.94),
D(v) =
∞
Z
0
dτ e
−λτ
B
1
λ
e
λτ
− 1
v, τ
.
For a sufficiently small friction (λτ
0
1), the solution to Eq. (8.95) has the form
P(v) = C exp
(
−
λv
2
2σ
2
f
τ
0
1 +
2
3
|v|τ
0
l
0
)
. (8.96)
For small particle velocity |v|τ
0
l
0
, probability distribution (8.96) grades
into the Gaussian distribution corresponding to the approximation of the delta-
correlated (in time) random field f (x, t). However, in the opposite limiting case
|v|τ
0
l
0
, probability distribution (8.96) decreases significantly faster than
in the case of the approximation of the delta-correlated (in time) random field
f (x, t), namely,
P(v) = C exp
(
−
λv
2
|v|
3σ
2
f
l
0
)
, (8.97)
which corresponds to the diffusion coefficient decreasing according to the law
D(v) ∼ 1/|v| for great particle velocities. Physically, it means that the effect of
random force f (x, t) on faster particles is significantly smaller than on slower
ones.

Lecture 9
Methods for Solving and Analyzing the
Fokker–Planck Equation
The Fokker–Planck equations for the one-point probability density (8.11), page 193,
and for the transitional probability density (8.16), page 195, are the partial differential
equations of parabolic type, so that we can use methods from the theory of mathemat-
ical physics equations to solve them. In this context, the basic methods are those such
as the method of separation of variables, Fourier transformation with respect to spatial
coordinates, and other integral transformations.
9.1 Integral Transformations
Integral transformations are very practicable for solving the Fokker–Planck equa-
tion. Indeed, earlier we mentioned the convenience of the Fourier transformation in
Eq. (8.11), page 193, if the tensor of diffusion coefficients F
kl
(x, x;t) is independent
of x. Different integral transformations related to eigenfunctions of the diffusion oper-
ator
b
L =
∂
2
∂x
k
∂x
l
F
kl
(x, x;t)
can be used in other situations.
For example, in the case of the Legendre operator
b
L =
∂
∂x
(x
2
− 1)
∂
∂x
,
it is quite natural to use the integral transformation related to the Legendre func-
tions. This transformation is called the Meler–Fock transform and is defined by
the formula
F(µ) =
∞
Z
1
dx f (x)P
−1/2+iµ
(x) (µ > 0), (9.1)
Lectures on Dynamics of Stochastic Systems. DOI: 10.1016/B978-0-12-384966-3.00009-X
Copyright
c
2011 Elsevier Inc. All rights reserved.

230 Lectures on Dynamics of Stochastic Systems
where P
−1/2+iµ
(x) is the complex index Legendre function of the first kind, which
satisfies the equation
d
dx
(x
2
− 1)
d
dx
P
−1/2+iµ
(x) = −
µ
2
+
1
4
P
−1/2+iµ
(x). (9.2)
The inversion of the transform (9.1) has the form
f (x) =
∞
Z
0
dµ µ tanh(πµ)F(µ)P
−1/2+iµ
(x) (1 ≤ x ≤ ∞), (9.3)
where F(µ) is given by formula (9.1).
Another integral transformation called the Kontorovich–Lebedev transform, is
related to the diffusion operator
b
L =
∂
∂x
x
2
∂
∂x
and has the form
F(τ ) =
∞
Z
0
dx f (x)K
iτ
(x) (τ > 0), (9.4)
where K
iτ
(x) is the imaginary index McDonald’s function of the first kind, which satis-
fies the equations
x
2
d
2
dx
2
+ x
d
dx
− x
2
+ τ
2
K
iτ
(x) = 0,
d
dx
x
2
d
dx
− x
d
dx
K
iτ
(x) =
x
2
− τ
2
K
iτ
(x).
(9.5)
The corresponding inversion has the form
f (x) =
2
π
2
x
∞
Z
0
dτ sinh(πτ )F(τ)K
iτ
(x). (9.6)
9.2 Steady-State Solutions of the Fokker–Planck Equation
In previous sections, we discussed the general methods for solving the Fokker–Planck
equation for both transition and one-point probability densities. However, the prob-
lem of the one-point probability density can have peculiarities related to the possible
Methods for Solving and Analyzing the Fokker–Planck Equation 231
existence of the steady-state solution; in a number of cases, such a solution can be
obtained immediately. The steady-state solution, if it exists, is independent of initial
values and is the solution of the Fokker–Planck equation in the limit t → ∞.
There are two classes of problems for which the steady-state solution of the
Fokker–Planck equation can be easily found. These classes deal with one-dimensional
differential equations and with the Hamiltonian systems of equations. We will consider
them in greater detail.
9.2.1 One-Dimensional Nonlinear Differential Equation
The one-dimensional nonlinear systems are described by the stochastic equation
d
dt
x(t) = f (x) + z(t)g(x), x(0) = x
0
, (9.7)
where z(t) is, as earlier, the Gaussian delta-correlated process with the parameters
h
z(t)
i
= 0,
z(t)z(t
0
)
= 2Dδ(t − t
0
) (D = σ
2
z
τ
0
).
The corresponding Fokker–Planck equation has the form
∂
∂t
+
∂
∂x
f (x)
P(x, t) = D
∂
∂x
g(x)
∂
∂x
g(x)P(x, t). (9.8)
The steady-state probability distribution P(x), if it exists, satisfies the equation
f (x)P(x) = Dg(x)
d
dx
g(x)P(x) (9.9)
(we assume that P(x) is distributed over the whole space, i.e., for −∞ < x < ∞)
whose solution is as follows
P(x) =
C
|g(x)|
exp
1
D
Z
dx
f (x)
g
2
(x)
, (9.10)
where constant C is determined from the normalization condition
∞
Z
−∞
dxP(x) = 1.
In the special case of the Langevin equation (8.60), page 211,
f (x) = −λx, g(x) = 1,

232 Lectures on Dynamics of Stochastic Systems
Eq. (9.10) grades into the Gaussian probability distribution
P(x) =
r
λ
2πD
exp
−
λ
2D
x
2
. (9.11)
9.2.2 Hamiltonian Systems
Another type of dynamic system that allows us to obtain the steady-state probability
distribution for N particles is described by the Hamiltonian system of equations with
linear friction and external random forces
d
dt
r
i
(t) =
∂
∂p
i
H({r
i
}, {p
i
}),
d
dt
p
i
(t) = −
∂
∂r
i
H({r
i
}, {p
i
}) − λp
i
+ f
i
(t),
(9.12)
where i = 1, 2, . . . , N;
H({r
i
}, {p
i
}) =
N
X
i=1
p
2
i
(t)
2
+ U(r
1
, . . . , r
N
)
is the Hamiltonian function; {r
i
}, {p
i
} stand for the totalities of all quantities r(t) and
p(t), i.e.,
{r
i
} = {r
1
, . . . , r
N
}, {p
i
} = {p
1
, . . . , p
N
};
λ is a constant coefficient (friction), and random forces f
i
(t) are the Gaussian delta-
correlated random vector functions with the correlation tensor
D
f
α
i
(t) f
β
j
(t
0
)
E
= 2Dδ
ij
δ
αβ
δ(t − t
0
), D = σ
2
f
τ
0
. (9.13)
Here, α and β are the vector indices.
The system of equations (9.12) describes the Brownian motion of a system of N
interacting particles. The corresponding indicator function ϕ({r
i
}, {p
i
}, t) satisfies the
equation
∂
∂t
ϕ({r
i
}, {p
i
}, t) +
N
X
k=1
{H, ϕ}
(k)
− λ
N
X
k=1
∂
∂p
k
{p
k
ϕ} =
N
X
k=1
∂
∂p
k
{f
k
(t)ϕ},
which is a generalization of Eq. (3.58), page 85, and, consequently, the Fokker–Planck
equation for the joint probability density of the solution to system (9.12) has the form
∂
∂t
P({r
i
}, {p
i
}, t) +
N
X
k=1
{H, P({r
i
}, {p
i
}, t)}
(k)
− λ
N
X
k=1
∂
∂p
k
p
k
P({r
i
}, {p
i
}, t)
= D
N
X
k=1
∂
2
∂p
2
k
P({r
i
}, {p
i
}, t), (9.14)
Methods for Solving and Analyzing the Fokker–Planck Equation 233
where
{ϕ, ψ}
(k)
=
∂ϕ
∂p
k
∂ψ
∂r
k
−
∂ψ
∂p
k
∂ϕ
∂r
k
is the Poisson bracket for the kth particle.
One can easily check that the steady-state solution to Eq. (9.14) is the canonical
Gibbs distribution
P({r
i
}, {p
i
}) = C exp
−
λ
D
H({r
i
}, {p
i
})
. (9.15)
The specificity of this distribution consists in the Gaussian behavior with respect to
momenta and statistical independence of particle coordinates and momenta.
Integrating Eq. (9.15) over all r, we can obtain the Maxwell distribution that des-
cribes velocity fluctuations of the Brownian particles. The case U(r
1
, . . . , r
N
) = 0
corresponds to the Brownian motion of a system of free particles.
If we integrate probability distribution (9.15) over momenta (velocities), we obtain
the Boltzmann distribution of particle coordinates
P({r
i
}) = C exp
−
λ
D
U({r
i
})
. (9.16)
In the case of sufficiently strong friction, the equilibrium distribution (9.15) is
formed in two stages. First, the Gaussian momentum distribution (the Maxwell dis-
tribution) is formed relatively quickly and then, the spatial distribution (the Boltz-
mann distribution) is formed at a much slower rate. The latter stage is described by
the Fokker–Planck equation
∂
∂t
P({r
i
}, t) =
1
λ
N
X
k=1
∂
∂r
k
∂U({r
i
})
∂r
k
P({r
i
}, t)
+
D
λ
2
N
X
k=1
∂
2
∂r
2
k
P({r
i
}, t), (9.17)
which is usually called the Einstein–Smolukhovsky equation. Derivation of Eq. (9.17)
from the Fokker–Planck equation (9.14) is called Kramers problem (see, e.g., the cor-
responding discussion in Sect. 6.2.1, page 144), where dynamics of particles under
a random force is considered as an example). Note that Eq. (9.17) statistically corre-
sponds to the stochastic equation
d
dt
r
i
(t) = −
1
λ
∂
∂r
i
U({r
i
}) +
1
λ
f
i
(t), (9.18)
which, nevertheless, cannot be considered as the limit of Eq. (9.12) for λ → ∞.
In the one-dimensional case, Eqs. (9.12) are simplified and assume the form of the
system of two equations
d
dt
x(t) = y(t),
d
dt
y(t) = −
∂
∂x
U(x) − λy(t) + f (t). (9.19)
234 Lectures on Dynamics of Stochastic Systems
The corresponding steady-state probability distribution has the form
P(x, y) = C exp
−
λ
D
H(x, y)
, H(x, y) =
y
2
2
+ U(x). (9.20)
9.2.3 Systems of Hydrodynamic Type
In Sect. 1.1.3, page 10, we considered the general dynamics of simplest
hydrodynamic-type systems (HTS). Now, we consider these systems in terms of the
statistical description.
Hydrodynamic-type systems with linear friction are described by the dynamic
equations
d
dt
v
i
(t) = F
i
(v) − λ
(i)
v
i
(t) (i = 1, . . . , N), (9.21)
where λ
(i)
is the friction coefficient of the i-th component of the N-dimensional vector
v
1
and F
i
(v) is the function quadratic in v and having the following properties:
(a) v
i
F
i
(v) = 0,
energy conservation holds at λ
(i)
= 0:
d
dt
E(t) = 0, E(t) =
v
2
i
(t)
2
;
(b)
∂
∂v
i
F
i
(v) = 0,
conditions of the Liouville theorem are satisfied at λ
(i)
= 0, and this equality
is the equation of incompressibility in the phase space.
Equilibrium Thermal Fluctuations in the Hydrodynamic-Type Systems
Here, we dwell on a class of phenomena closely related to the Brownian motion;
namely, we dwell on equilibrium thermal fluctuations in solids.
Microscopic equations describe the behavior of physical systems only in terms of
spatial scales large in comparison with the molecule free path in the medium and tem-
poral scales great in comparison with the time intervals between molecule collisions.
This means that macroscopic equations adequately describe the behavior of systems
only on average. However, in view of molecule thermal motion, macroscopic vari-
ables are in general terms stochastic variables, and a complete macroscopic theory
must describe not only system behavior on average, but also the fluctuations about the
average.
1
In the general case, the dissipative term in Eq. (9.21) has the form λ
ik
v
k
. However, we can always choose
the coordinate system in which two positively defined quadratic forms – energy E = v
2
i
/2 and dissipation
λ
ik
v
i
v
k
– have the diagonal representation. The form of Eq. (9.21) assumes the use of namely such a
coordinate system.
Methods for Solving and Analyzing the Fokker–Planck Equation 235
Such a description can be performed in terms of macroscopic variables by supple-
menting the corresponding macroscopic equations with the ‘external forces’ specified
as the Gaussian random fields delta-correlated in time (this approach is closely related
to the fluctuation – dissipation theorem, or the Callen–Welton theorem). See [53, 54]
for the corresponding correlation theories of equilibrium thermal fluctuations in elec-
trodynamics, hydrodynamics, and viscoelastic media.
In HTS, equilibrium thermal fluctuations are described by Eq. (9.21) supplemented
with external forces f
i
(t)
d
dt
v
i
(t) = F
i
(v) − λ
(i)
v
i
(t) + f
i
(t) (i = 1, . . . , N). (9.22)
External forces are assumed to be the Gaussian random functions delta-correlated in
time with the correlation tensor of the form
f
i
(t)f
j
(t
0
)
= 2δ
ij
σ
2
(i)
δ(t − t
0
) (
h
f (t)
i
= 0). (9.23)
Note that one can consider Eqs. (9.22) as the system describing the Brownian
motion in HTS. Such a treatment assumes that coefficients λ
(i)
are certain effective
friction coefficients. For example, at N = 3, system (9.22) describes (in the velocity
space) the rotary Brownian motion of a solid in a medium, and quantities λ
(i)
v
i
(t) play
the role of the corresponding resistance forces. The probability density of solution
v(t) to Eqs. (9.22), i.e., function P(v, t) =
h
δ(v(t) − v)
i
, satisfies the Fokker–Planck
equation
∂
∂t
P(v, t) = −
∂
∂v
i
{
F
i
(v)P(v, t)
}
+ λ
(i)
∂
∂v
i
{
v
i
P(v, t)
}
+ σ
2
(i)
∂
2
∂v
2
i
P(v, t). (9.24)
The steady-state, initial data-independent solution to Eq. (9.24) must behave like
the Maxwell distribution that corresponds to the uniform distribution of energy over
the degrees of freedom
P(v) = C exp
(
−
v
2
i
2kT
)
, (9.25)
where k is the Boltzmann constant and T is the equilibrium temperature in the system.
Substituting Eq. (9.25) in Eq. (9.24), we obtain the expression for σ
2
(i)
σ
2
(i)
= λ
(i)
kT (9.26)
called the Einstein formula. Here, we used that, in view of conditions (a) and (b),
∂
∂v
i
{
F
i
(v)P(v)
}
= 0.
