Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.


186 Lectures on Dynamics of Stochastic Systems
If operators
b
A(t) and
b
B(t) are the time-independent matrices A and B, we can solve
system (7.10) using the Laplace transform. After the Laplace transform, system (7.10)
grades into the algebraic system of equations
(pE − A)
h
x
i
p
− Bψ
ψ
ψ
p
= x
0
,
[
(
p + 2ν
)
E − A]ψ
ψ
ψ
p
− a
2
0
B
h
x
i
p
= 0,
(7.11)
where E is the unit matrix. From this system, we obtain solution
h
x
i
p
in the form
h
x
i
p
=
(pE − A) − a
2
0
B
1
(p + 2ν)E − A
B
−1
x
0
. (7.12)
Assume now operators
b
A(t) and
b
B(t) in Eq. (7.6) be the matrices. If only one com-
ponent is of interest, we can obtain for it the operator equation
b
L
d
dt
x(t) +
n−1
X
i+j=0
b
ij
(t)
d
i
dt
i
z(t)
d
j
dt
j
x(t) = f (t), (7.13)
where
b
L
d
dt
=
n
X
i=0
a
i
(t)
d
i
dt
i
and n is the order of matrices A and B in Eq. (7.6). The initial conditions for x are
included in function f (t) through the corresponding derivatives of delta function. Note
that function f (t) can depend additionally on derivatives of random process z(t) at
t = 0, i.e., f (t) is also the random function statistically related to process z(t).
Averaging Eq. (7.13) over an ensemble of realizations of process z(t) with the use
of formula (7.5), we obtain the equation
b
L
d
dt
h
x(t)
i
+ M
d
dt
,
d
dt
+ 2ν
h
z(t)x(t)
i
=
h
f (t)
i
, (7.14)
where
M
[
p, q
]
=
n−1
X
i+j=0
b
ij
(t)p
i
q
j
.
However, Eq. (7.14) is unclosed because of the presence of correlation
h
z(t)x(t)
i
.
Multiplying Eq. (7.13) by z(t) and averaging the result, we obtain the equation for
correlation
h
z(t)x(t)
i
b
L
d
dt
+ 2ν
h
z(t)x(t)
i
+ a
2
0
M
d
dt
+ 2ν,
d
dt
h
x(t)
i
=
h
z(t)f (t)
i
. (7.15)

Stochastic Equations with the Markovian Fluctuations of Parameters 187
System of equations (7.14) and Eq. (7.15) is the closed system. If functions a
i
(t)
and b
ij
(t) are independent of time, this system can be solved using Laplace transform.
The solution is as follows:
h
x
i
p
=
b
L(p + 2ν)
h
f
i
p
− M[p, p + 2ν]
h
z f
i
p
b
L(p)
b
L(p + 2ν) − a
2
0
M[p + 2ν, p]M[p, p + 2ν]
. (7.16)
7.2 Gaussian Markovian Processes
Here, we consider several examples associated with the Gaussian Markovian pro-
cesses.
Define random process z(t) by the formula
z(t) = z
1
(t) + · · · + z
N
(t), (7.17)
where z
i
(t) are statistically independent telegrapher’s processes with correlation func-
tions
z
i
(t)z
j
(t
0
)
= δ
ij
D
z
2
E
e
−α|t−t
0
|
(α = 2ν).
If we set
z
2
= σ
2
/N, then this process grades for N → ∞ into the Gaussian
Markovian process with correlation function
z
i
(t)z
j
(t
0
)
=
D
z
2
E
e
−α|t−t
0
|
.
Thus, process z(t) (7.17) approximates the Gaussian Markovian process in terms of
the Markovian process with a finite number of states.
It is evident that the differentiation formula and the rule of factoring the derivative
out of averaging brackets for process z(t) assume the forms
d
dt
+ αk
h
z
1
(t) · · · z
k
(t)R[t; z(τ )]
i
=
z
1
(t) · · · z
k
(t)
d
dt
R[t; z(τ )]
,
z
1
(t) · · · z
k
(t)
d
n
dt
n
R[t; z(τ )]
=
d
dt
+ αk
n
h
z
1
(t) · · · z
k
(t)R[t; z(τ )]
i
,
(7.18)
where R[t; z(τ )] is an arbitrary functional of process z(t) (τ ≤ t).
Consider again Eq. (7.6), which we represent here in the form
d
dt
x(t) =
b
A(t)x(t) + [z
1
(t) + · · · + z
N
(t)]
b
B(t)x(t), x(0) = x
0
, (7.19)
and introduce vector-function
X
k
(t) =
h
z
1
(t) . . . z
k
(t)x(t)
i
, k = 1, . . . , N; X
0
(t) =
h
x(t)
i
. (7.20)

188 Lectures on Dynamics of Stochastic Systems
Using formula (7.18) for differentiating correlations (7.20) and Eq. (7.19), we
obtain the recurrence equation for x
k
(t) (k = 0, 1, . . . , N)
d
dt
X
k
(t) =
b
A(t)X
k
(t) +
z
1
(t) · · · z
k
(t)[z
1
(t) + · · · + z
N
(t)]
b
B(t)x(t)
=
b
A(t)X
k
(t) + k
D
z
2
E
b
B(t)X
k−1
(t) + (N − k)
b
B(t)X
k+1
(t), (7.21)
with the initial condition
X
k
(0) = x
0
δ
k,0
.
Thus, the mean value of the solution to system Eq. (7.19) satisfies the closed system
of
(
N + 1
)
vector equations. If operators
b
A(t),
b
B(t) are time-independent matrices,
system (7.21) can be easily solved using the Laplace transform. It is clear that such a
solution will have the form of a finite segment of continued fraction. If we set
z
2
=
σ
2
/N and proceed to the limit N → ∞, then random process (7.17) will grade, as was
mentioned earlier, into the Gaussian Markovian process and solution to system (7.21)
will assume the form of the infinite continued fraction.
Problems
Problem 7.1
Assuming that z(t) is telegrapher’s random process, find average potential
energy of the stochastic oscillator described by the equation
d
3
dt
3
U(t) + 4ω
2
0
d
dt
U(t) + 2ω
2
0
z(t)
d
dt
U(t) +
d
dt
z(t)U(t)
= 0,
x(0) = 0,
d
dt
U(t)
t=0
= 0,
d
2
dt
2
U(t)
t=0
= 2y
2
0
.
Solution
d
3
dt
3
h
U(t)
i
+ 4ω
2
0
d
dt
h
U(t)
i
+ 4ω
2
0
d
dt
+ 2ν
h
z(t)U(t)
i
= 0,
d
dt
+ 2ν
3
h
z(t)U(t)
i
+ 4ω
2
0
d
dt
+ 2ν
h
z(t)U(t)
i
+ 4ω
2
0
a
2
0
d
dt
+ 2ν
h
U(t)
i
= 0. (7.22)

Stochastic Equations with the Markovian Fluctuations of Parameters 189
System of equations (7.22) can be solved using Laplace transform, and we obtain
the solution in the form
h
U
i
p
= 2y
2
0
L(p + 2ν)
L(p)L(p + 2ν) − a
2
0
M
2
(p)
,
L(p) = p
p
2
+ 4ω
2
0
, M(p) = 4ω
2
0
p
2
+ ν
.
(7.23)
Remark In the limiting case of great parameters ν and a
2
0
, but finite ratio a
2
0
/2ν =
σ
2
τ
0
, we obtain from the second equation of system (7.22)
h
z(t)U(t)
i
= −
ω
2
0
σ
2
τ
0
ν
h
U(t)
i
.
Consequently, average potential energy
h
U(t)
i
satisfies in this limiting case the
closed third-order equation
d
3
dt
3
h
U(t)
i
+ 4ω
2
0
d
dt
h
U(t)
i
− 4ω
4
0
σ
2
τ
0
h
U(t)
i
= 0,
which coincides with Eq. (6.92), page 173, and corresponds to the Gaussian
delta-correlated process z(t).
Problem 7.2
Assuming that z(t) is telegrapher’s random process, obtain the steady-state
probability distribution of the solution to the stochastic equation
d
dt
x(t) = f (x) + z(t)g(x), x(0) = x
0
.
Solution Under the condition that | f (x)| < a
0
|g(x)|, we have
P(x) =
C|g(x)|
a
2
0
g
2
(x) − f
2
(x)
exp
(
2ν
a
2
0
Z
dx
f (x)
a
2
0
g
2
(x) − f
2
(x)
)
, (7.24)
where the positive constant C is determined from the normalization condition.
190 Lectures on Dynamics of Stochastic Systems
Remark In the limit ν → ∞ and a
2
0
→ ∞ under the condition that a
2
0
τ
0
= const
(τ
0
= 1/
(
2ν
)
), probability distribution (7.24) grades into the expression
P(x) =
C
|g(x)|
exp
(
2ν
a
2
0
Z
dx
f (x)
g
2
(x)
)
corresponding to the Gaussian delta-correlated process z(t), i.e., the Gaussian
process with correlation function
z(t)z(t
0
)
= 2a
2
0
τ
0
δ(t − t
0
).
Problem 7.3
Assuming that z(t) is telegrapher’s random process, obtain the steady-state
probability distribution of the solution to the stochastic equation
d
dt
x(t) = −x + z(t), x(0) = x
0
. (7.25)
Solution
P(x) =
1
B(ν, 1/2)
(1 − x
2
)
ν−1
(|x| < 1), (7.26)
where B(ν, 1/2) is the beta-function. This distribution has essentially different
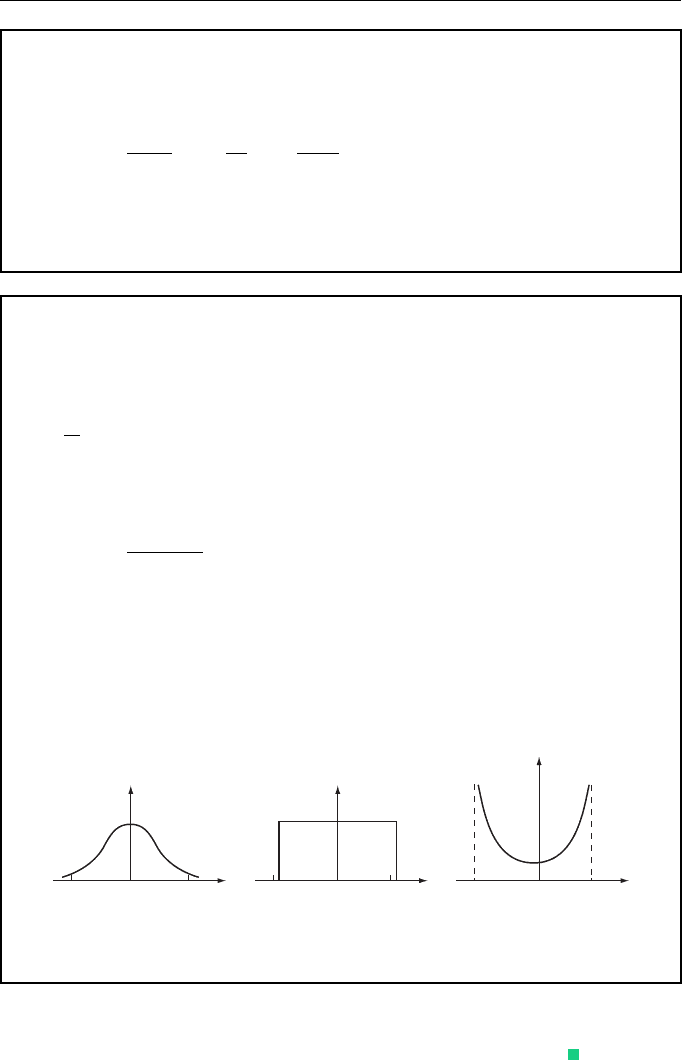
behaviors for ν > 1, ν = 1 and ν < 1. One can easily see that this system
resides mainly near state x = 0 if ν > 1, and near states x = ±1 if ν < 1. In the
case ν = 1, we obtain the uniform probability distribution on segment [−1, 1]
(Fig. 7.1).
x
1
−1
x
1
−1
x
1
−1
P(x) P(x)
ν =1
ν >1
P(x)
ν <1
Figure 7.1 Steady-state probability distribution (7.26) of the solution to the Eq. (7.25)
versus parameter ν.

Lecture 8
Approximations of Gaussian Random
Field Delta-Correlated in Time
In the foregoing Lectures, we considered in detail the general methods of analyzing
stochastic equations. Here, we give an alternative and more detailed consideration
of the approximation of the Gaussian random delta-correlated (in time) field in the
context of stochastic equations and discuss the physical meaning of this widely used
approximation.
8.1 The Fokker–Planck Equation
Let vector function x(t) = {x
1
(t), x
2
(t), . . . , x
n
(t)} satisfies the dynamic equation
d
dt
x(t) = v(x, t) + f (x, t), x(t
0
) = x
0
, (8.1)
where v
i
(x, t) (i = 1, . . . , n) are the deterministic functions and f
i
(x, t) are the random
functions of (n + 1) variable that have the following properties:
(a) f
i
(x, t) is the Gaussian random field in the (n + 1)-dimensional space (x, t);
(b)
h
f
i
(x, t)
i
= 0.
For definiteness, we assume that t is the temporal variable and x is the spatial
variable.
Statistical characteristics of field f
i
(x, t) are completely described by correlation
tensor
B
ij
(x, t;x
0
, t
0
) =
f
i
(x, t)f
j
(x
0
, t
0
)
.
Because Eq. (8.1) is the first-order equation with the initial value, its solution satis-
fies the dynamic causality condition
δ
δf
j
(x
0
, t
0
)
x
i
(t) = 0 for t
0
< t
0
andt
0
> t, (8.2)
Lectures on Dynamics of Stochastic Systems. DOI: 10.1016/B978-0-12-384966-3.00008-8
Copyright
c
2011 Elsevier Inc. All rights reserved.

192 Lectures on Dynamics of Stochastic Systems
which means that solution x(t) depends only on values of function f
j
(x, t
0
) for times t
0
preceding time t, i.e., t
0
≤ t
0
≤ t. In addition, we have the following equality for the
variational derivative
δ
δf
j
(x
0
, t − 0)
x
i
(t) = δ
ij
δ(x(t) − x
0
). (8.3)
Nevertheless, the statistical relationship between x(t) and function values f
j
(x, t
00
)
for consequent times t
00
> t can exist, because such function values f
j
(x, t
00
) are corre-
lated with values f
j
(x, t
0
) for t
0
≤ t. It is obvious that the correlation between function
x(t) and consequent values f
j
(x, t
00
) is appreciable only for t
00
−t ≤ τ
0
, where τ
0
is the
correlation radius of field f(x, t) with respect to variable t.
For many actual physical processes, characteristic temporal scale T of function
x(t) significantly exceeds correlation radius τ
0
(T τ
0
); in this case, the problem has
small parameter τ
0
/T that can be used to construct an approximate solution.
In the first approximation with respect to this small parameter, one can consider the
asymptotic solution for τ
0
→ 0. In this case values of function x(t
0
) for t
0
< t will be
independent of values f (x, t
00
) for t
00
> t not only functionally, but also statistically.
This approximation is equivalent to the replacement of correlation tensor B
ij
with the
effective tensor
B
eff
ij
(x, t;x
0
, t
0
) = 2δ(t − t
0
)F
ij
(x, x
0
;t). (8.4)
Here, quantity F
ij
(x, x
0
, t) is determined from the condition that integrals of
B
ij
(x, t;x
0
, t
0
) and B
eff
ij
(x, t;x
0
, t
0
) over t
0
coincide
F
ij
(x, x
0
, t) =
1
2
∞
Z
−∞
dt
0
B
ij
(x, t;x
0
, t
0
),
which just corresponds to the passage to the Gaussian random field delta-correlated in
time t.
Introduce the indicator function
ϕ(x, t) = δ(x
(
t
)
− x), (8.5)
where x(t) is the solution to Eq. (8.1), which satisfies the Liouville equation
∂
∂t
+
∂
∂x
v(x, t)
ϕ(x, t) = −
∂
∂x
f (x, t)ϕ(x, t) (8.6)
and the equality
δ
δf
j
(x
0
, t − 0)
ϕ(x, t) = −
∂
∂x
j
δ(x − x
0
)ϕ(x, t)
. (8.7)

Approximations of Gaussian Random Field Delta-Correlated in Time 193
The equation for the probability density of the solution to Eq. (8.1)
P(x, t) =
h
ϕ(x, t)
i
=
h
δ(x(t) − x)
i
can be obtained by averaging Eq. (8.6) over an ensemble of realizations of field
f (x, t),
∂
∂t
+
∂
∂x
v(x, t)
P(x, t) = −
∂
∂x
h
f (x, t)ϕ(x, t)
i
. (8.8)
We rewrite Eq. (8.8) in the form
∂
∂t
+
∂
∂x
v(x, t)
P(x, t)
= −
∂
∂x
i
Z
dx
0
t
Z
t
0
dt
0
B
ij
(x, t;x
0
, t
0
)
δϕ(x, t)
δf
j
(x
0
, t
0
)
, (8.9)
where we used the Furutsu–Novikov formula (5.13), page 126,
h
f
k
(x, t)R[t;f(y, τ )]
i
=
Z
dx
0
Z
dt
0
B
kl
(x, t;x
0
, t
0
)
δR[t;f(y, τ )]
δ f
l
(x
0
, t
0
)
(8.10)
for the correlator of the Gaussian random field f (x, t) with arbitrary functional
R[t;f (y, τ )] of it and the dynamic causality condition (8.2).
Equation (8.9) shows that the one-time probability density of solution x(t) at instant
t is governed by functional dependence of solution x(t) on field f (x
0
, t) for all times in
the interval (t
0
, t).
In the general case, there is no closed equation for the probability density P(x, t).
However, if we use approximation (8.4) for the correlation function of field f (x, t),
there appear terms related to variational derivatives δϕ[x, t;f (y, τ )]/δf
j
(x
0
, t
0
) at coin-
cident temporal arguments t
0
= t − 0,
∂
∂t
+
∂
∂x
v(x, t)
P(x, t) = −
∂
∂x
i
Z
dx
0
F
ij
(x, x
0
, t)
δϕ(x, t)
δf
j
(x
0
, t − 0)
.
According to Eq. (8.7), these variational derivatives can be expressed immediately in
terms of quantity ϕ[x, t;f(y, τ )]. Thus, we obtain the closed Fokker-Planck equation
∂
∂t
+
∂
∂x
k
[
v
k
(x, t) + A
k
(x, t)
]
P(x, t) =
∂
2
∂x
k
∂x
l
[
F
kl
(x, x, t)P(x, t)
]
, (8.11)
where
A
k
(x, t) =
∂
∂x
0
l
F
kl
(x, x
0
, t)
x
0
=x
.

194 Lectures on Dynamics of Stochastic Systems
Equation (8.11) should be solved with the initial condition
P(x, t
0
) = δ(x − x
0
),
or with a more general initial condition P(x, t
0
) = W
0
(x) if the initial conditions are
also random, but statistically independent of field f(x, t).
The Fokker–Planck equation (8.11) is a partial differential equation and its further
analysis essentially depends on boundary conditions with respect to x whose form can
vary depending on the problem at hand.
Consider the quantities appeared in Eq. (8.11). In this equation, the terms contain-
ing A
k
(x, t) and F
kl
(x, x
0
, t) are stipulated by fluctuations of field f (x, t). If field f(x, t)
is stationary in time, quantities A
k
(x) and F
kl
(x, x
0
) are independent of time. If field
f (x, t) is additionally homogeneous and isotropic in all spatial coordinates, then
F
kl
(x, x, t) = const,
which corresponds to the constant tensor of diffusion coefficients, and A
k
(x, t) = 0
(note however that quantities F
kl
(x, x
0
, t) and A
k
(x, t) can depend on x because of the
use of a curvilinear coordinate systems).
8.2 Transition Probability Distributions
Turn back to dynamic system (8.1) and consider the m-time probability density
P
m
(x
1
, t
1
;. . . ;x
m
, t
m
) =
h
δ(x(t
1
) − x
1
) ···δ(x(t
m
) − x
m
)
i
(8.12)
for m different instants t
1
< t
2
< ··· < t
m
. Differentiating Eq. (8.12) with respect
to time t
m
and using then dynamic equation (8.1), dynamic causality condition (8.2),
definition of function F
kl
(x, x
0
, t), and the Furutsu–Novikov formula (8.10), one can
obtain the equation similar to the Fokker–Planck equation (8.11),
∂
∂t
m
P
m
(x
1
, t
1
;. . . ;x
m
, t
m
)
+
n
X
k=1
∂
∂x
mk
[
v
k
(x
m
, t
m
) + A
k
(x
m
, t
m
)
]
P
m
(x
1
, t
1
;. . . ;x
m
, t
m
)
=
n
X
k=1
n
X
l=1
∂
2
∂x
mk
∂x
ml
[
F
kl
(x
m
, x
m
, t
m
)P
m
(x
1
, t
1
;. . . ;x
m
, t
m
))
]
. (8.13)
No summation over index m is performed here. The initial value to Eq. (8.13) can
be determined from Eq. (8.12). Setting t
m
= t
m−1
in (8.12), we obtain
P
m
(x
1
, t
1
;. . . ;x
m
, t
m−1
)
= δ(x
m
− x
m−1
)P
m−1
(x
1
, t
1
;. . . ;x
m−1
, t
m−1
). (8.14)

Approximations of Gaussian Random Field Delta-Correlated in Time 195
Equation (8.13) assumes the solution in the form
P
m
(x
1
, t
1
;. . . ;x
m
, t
m
)
= p(x
m
, t
m
|x
m−1
, t
m−1
)P
m−1
(x
1
, t
1
;. . . ;x
m−1
, t
m−1
). (8.15)
Because all differential operations in Eq. (8.13) concern only t
m
and x
m
, we can
find the equation for the transitional probability density by substituting Eq. (8.15) in
Eq. (8.13) and (8.14):
∂
∂t
+
∂
∂x
k
[
v
k
(x, t) + A
k
(x, t)
]
p(x, t|x
0
, t
0
)
=
∂
2
∂x
k
∂x
l
[
F
kl
(x, x, t)p(x, t|x
0
, t
0
)
]
(8.16)
with initial condition
p(x, t|x
0
, t
0
)|
t→t
0
= δ(x − x
0
),
where
p(x, t|x
0
, t
0
) =
h
δ(x(t) − x)|x(t
0
) = x
0
i
.
In Eq. (8.16) we denoted variables x
m
and t
m
as x and t, and variables x
m−1
and
t
m−1
as x
0
and t
0
.
Using formula (8.15) (m − 1) times, we obtain the relationship
P
m
(x
1
, t
1
;. . . ;x
m
, t
m
)
= p(x
m
, t
m
|x
m−1
, t
m−1
) ···p(x
2
, t
2
|x
1
, t
1
)P(x
1
, t
1
), (8.17)
where P(x
1
, t
1
) is the one-time probability density governed by Eq. (8.11). Equal-
ity (8.17) expresses the multi-time probability density as the product of transitional
probability densities, which means that random process x(t) is the Markovian process.
Equation (8.11) is usually called the forward Fokker–Planck equation. The back-
ward Fokker–Planck equation (it describes the transitional probability density as a
function of the initial parameters t
0
and x
0
) can also be easily derived.
Indeed, in Lecture 3 (page 69), we obtained the backward Liouville equation (3.8),
page 71, for indicator function
∂
∂t
0
+ v(x
0
, t
0
)
∂
∂x
0
ϕ(x, t|x
0
, t
0
) = −f(x
0
, t
0
)
∂
∂x
0
ϕ(x, t|x
0
, t
0
), (8.18)
with the initial value ϕ(x, t|x
0
, t) = δ(x − x
0
). This equation describes the dynamic
system evolution in terms of initial parameters t
0
and x
0
. From Eq. (8.18) follows the
equality similar to Eq. (8.7),
δ
δf
j
(x
0
, t
0
+ 0)
ϕ(x, t|x
0
, t
0
) = δ(x − x
0
)
∂
∂x
0j
ϕ(x, t|x
0
, t
0
). (8.19)
