Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.


156 Lectures on Dynamics of Stochastic Systems
where
D
ij
(t) =
1
2
d
dt
r
i
(t)r
j
(t)
=
1
2
r
i
(t)v
j
(t)
+
r
j
(t)v
i
(t)
=
t
Z
0
dτ B
ij
(τ )
1 − e
−λt
h
1 − e
−λ(t−τ )
i
.
is the diffusion tensor (6.27). Under the condition λt 1, we obtain the equation
∂
∂t
P(r, t) = D
ij
∂
2
∂r
i
∂r
j
P(r, t), P(r, 0) = δ
(
r
)
(6.49)
with the diffusion tensor
D
ij
=
∞
Z
0
dτ B
ij
(τ ). (6.50)
Note that conversion from Eq. (6.37) to the equation in probability density of parti-
cle coordinate (6.49) with the diffusion coefficient (6.50) corresponds to the so-called
Kramers problem.
Under the assumption that λτ
0
1, where τ
0
is the temporal correlation radius of
process f(t), Eq. (6.37) becomes simpler
∂
∂t
+ v
∂
∂r
− λ
∂
∂v
v
P(r, v, t) = λ
2
t
Z
0
dτ B
ij
(τ )
∂
2
∂v
i
∂v
j
P(r, v, t),
P(r, v; 0) = δ
(
r
)
δ
(
v
)
,
and corresponds to the approximation of random function f (t) by the delta-correlated
process. If t τ
0
, we can replace the upper limit of the integral with the infinity and
proceed to the standard diffusion Fokker–Planck equation
∂
∂t
+ v
∂
∂r
− λ
∂
∂v
v
P(r, v, t) = λ
2
D
ij
∂
2
∂v
i
∂v
j
P(r, v, t),
P(r, v; 0) = δ
(
r
)
δ
(
v
)
,
(6.51)
with diffusion tensor (6.50). In this approximation, the combined random process
{r(t), v(t)} is the Markovian process.
Under the condition λt 1, there are the steady-state equation for the probability
density of particle velocity
−λ
∂
∂v
vP(v) = λ
2
D
ij
∂
2
∂v
i
∂v
j
P(v),

General Approaches to Analyzing Stochastic Systems 157
and the nonsteady-state equation for the probability density of particle coordinate
∂
∂t
P(r, t) = D
ij
∂
2
∂r
i
∂r
j
P(r, t), P(r, 0) = δ
(
r
)
.
Consider now the limit λτ
0
1. In this case, we can rewrite Eq. (6.37) in the form
∂
∂t
+ v
∂
∂r
− λ
∂
∂v
v
P(r, v, t) = λB
ij
(0)
1 − e
−λt
∂
2
∂v
i
∂v
j
P(r, v, t)
− B
ij
(0)
1 − e
−λt
∂
2
∂v
i
∂r
j
P(r, v, t) + λ
t
Z
0
dτ B
ij
(τ )
∂
2
∂v
i
∂r
j
P(r, v, t),
P(r, v; 0) = δ
(
r
)
δ
(
v
)
.
Integrating this equation over r, we obtain the equation for the probability density of
particle velocity
∂
∂t
− λ
∂
∂v
v
P(v, t) = λB
ij
(0)
1 − e
−λt
∂
2
∂v
i
∂v
j
P(v, t),
P(v; 0) = δ
(
v
)
,
and, under the condition λt 1, we arrive at the steady-state Gaussian probability
density with variance
v
i
(t)v
j
(t)
= B
ij
(0).
As regards the probability density of particle position, it satisfies, under the condi-
tion λt 1, the equation
∂
∂t
P(r, t) = D
ij
∂
2
∂r
i
∂r
j
P(r, t), P(r, 0) = δ
(
r
)
(6.52)
with the same diffusion coefficient as previously. This is a consequence of the fact that
Eq. (6.44) is independent of parameter λ. Note that this equation corresponds to the
limit process λ → ∞ in Eq. (6.25)
d
dt
r(t) = v(t), v(t) = f (t), r(0) = 0.
In the limit λ → ∞ (or λτ
0
1), we have the equality
v(t) ≈ f (t), (6.53)

158 Lectures on Dynamics of Stochastic Systems
and all multi-time statistics of random functions v(t) and r(t) will be described in
terms of statistical characteristics of process f (t). In particular, the one-time probabi-
lity density of particle velocity v(t) is the Gaussian probability density with variance
v
i
(t)v
j
(t)
= B
ij
(0), and the spatial diffusion coefficient is
D =
1
2
d
dt
D
r
2
(t)
E
=
∞
Z
0
dτ B
ii
(τ ) = τ
0
B
ii
(0).
As we have seen earlier, in the case of process f (t) such that it can be correctly
described in the delta-correlated approximation (i.e., if λτ
0
1), the approximate
equality (6.53) appears inappropriate to determine statistical characteristics of process
v(t). Nevertheless, Eq. (6.52) with the same diffusion tensor remains as before valid
for the one-time statistical characteristics of process r(t), which follows from the fact
that Eq. (6.48) is valid for any parameter λ and arbitrary probability density of random
process f(t).
Above, we considered several types of stochastic ordinary differential equations
that allow obtaining closed statistical description in the general form. It is clear that
similar situations can appear in dynamic systems formulated in terms of partial diffe-
rential equations.
6.2.2 Partial Differential Equations
First of all, we note that the first-order partial differential equation
∂
∂t
+ z(t)g(t)
∂
∂x
F(x)
ρ(x, t) = 0, (6.54)
is equivalent to the system of ordinary differential equations (6.10), page 144 and, con-
sequently, also allows the complete statistical description for arbitrary given random
process z(t).
Solution ρ(r, t) to Eq. (6.54) is a functional of random process z(t) of the form
ρ(x, t) = ρ[x, t; z(τ)] = ρ(x, T[t; z(τ )]),
with functional
T[t; z(τ )] =
t
Z
0
dτ z(τ )g(τ ), (6.55)
so that Eq. (6.54) can be rewritten in the form
∂
∂T
+
∂
∂x
F(x)
ρ(x, T) = 0.
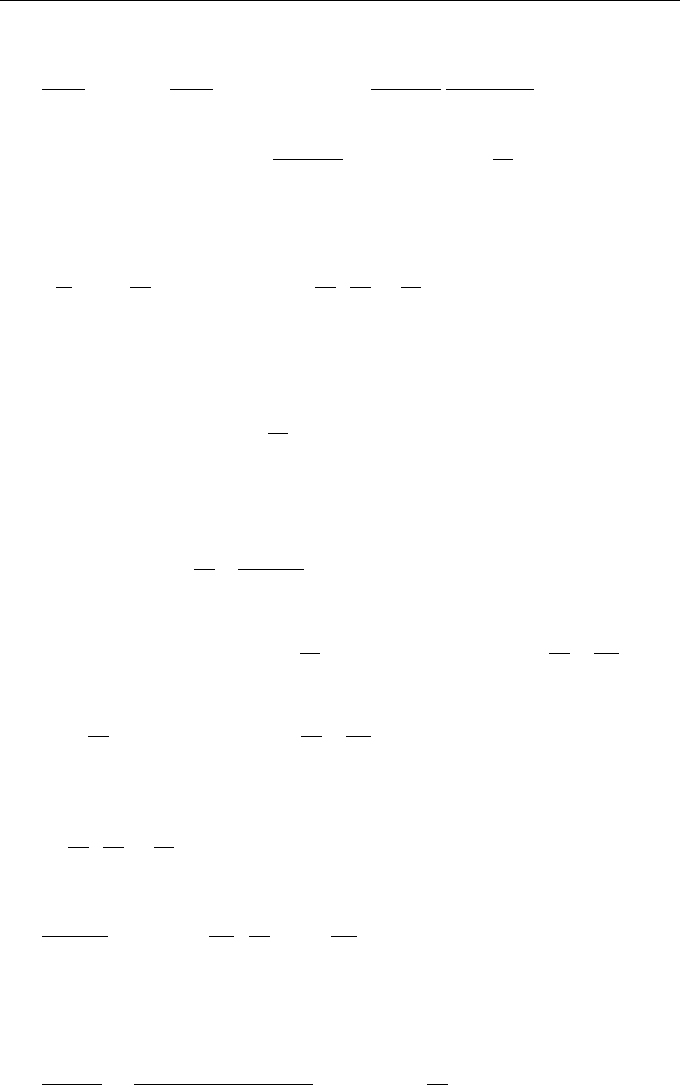
General Approaches to Analyzing Stochastic Systems 159
The variational derivative is expressed in this case as follows
δ
δz(τ )
ρ(x, t) =
δ
δz(τ )
ρ(x, T[t; z(τ )]) =
dρ(x, T)
dT
δT[t; z(τ )]
δz(τ )
= θ(t − τ )g(τ )
dρ(x, T)
dT
= −θ(t − τ )g(τ )
∂
∂x
F(x)ρ(x, t).
Consider now the class of nonlinear partial differential equations whose parameters
are independent of spatial variable x,
∂
∂t
+ z(t)
∂
∂x
q(x, t) = F
t, q,
∂q
∂x
,
∂
∂x
⊗
∂q
∂x
, . . .
, (6.56)
where z(t) is the vector random process and F is the deterministic function. Solution
to this equation is representable in the form
q(x, t) = exp
−
t
Z
0
dτ z(τ )
∂
∂x
Q
(
x, t
)
= Q
x −
t
Z
0
dτ z(τ ), t
, (6.57)
where we introduced the shift operator. Function Q(x, t) satisfies the equation
exp
−
t
Z
0
dτ z(τ )
∂
∂x
∂Q(x, t)
∂t
= F
t,
exp
−
t
Z
0
dτ z(τ )
∂
∂x
Q
,
exp
−
t
Z
0
dτ z(τ )
∂
∂x
∂Q
∂x
,
∂
∂x
⊗
exp
−
t
Z
0
dτ z(τ )
∂
∂x
∂Q
∂x
, . . . ,
. (6.58)
The shift operator can be factored out from arguments of function
F
t, q,
∂q
∂x
,
∂
∂x
⊗
∂q
∂x
, . . .
, and Eq. (6.58) assumes the form of the deterministic
equation
∂Q(x, t)
∂t
= F
t, Q,
∂Q
∂x
,
∂
∂x
⊗ exp
∂Q
∂x
, . . .
. (6.59)
Thus, the variational derivative can be expressed in the form
δq(x, t)
δz(τ )
=
δQ
x −
t
R
0
dτ z(τ ), t
!
δz(τ )
= −θ(t − τ )
∂
∂x
q(x, t), (6.60)
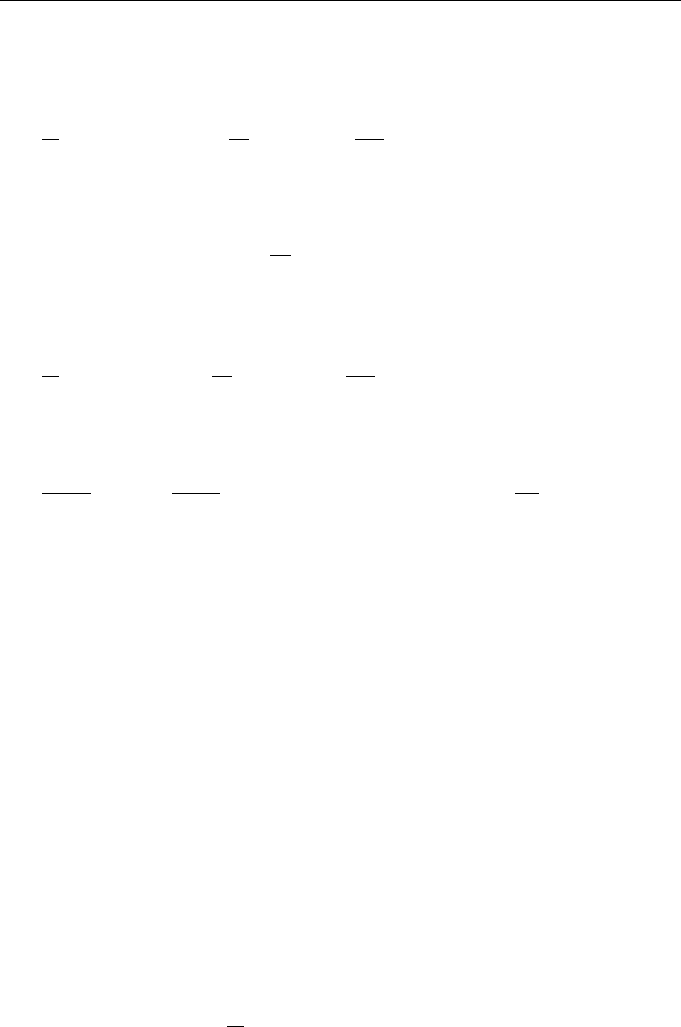
160 Lectures on Dynamics of Stochastic Systems
i.e., the variational derivatives of the solution to problem (6.56) are expressed in terms
of spatial derivatives.
Consider the Burgers equation with random drift z(t) as a specific example:
∂
∂t
v(x, t) +
(
v + z(t)
)
∂
∂x
v(x, t) = ν
∂
2
∂x
2
v(x, t). (6.61)
In this case, the solution has the form
v(x, t) = exp
−
t
Z
0
dτ z(τ )
∂
∂x
V(x, t) = V
x −
t
Z
0
dτ z(τ ), t
,
where function V(x, t) satisfies the standard Burgers equation
∂
∂t
V(x, t) +
V(x, t)
∂
∂x
V(x, t) = ν
∂
2
∂x
2
V(x, t). (6.62)
In this example, the variational derivative is given by the expression
δ
δz
i
(τ )
v(x, t) =
δ
δz
i
(τ )
V
x −
t
Z
0
dτ z(τ ), t
= −θ(t − τ )
∂
∂x
i
v(x, t). (6.63)
In the case of such problems, statistical characteristics of the solution can be deter-
mined immediately by averaging the corresponding expressions constructed from the
solution to the last equation.
Unfortunately, there is only limited number of equations that allow sufficiently
complete analysis. In the general case, the analysis of dynamic systems appears pos-
sible only on the basis of various asymptotic and approximate techniques. In physics,
techniques based on approximating actual random processes and fields by the fields
delta-correlated in time are often and successfully used.
6.3 Delta-Correlated Fields and Processes
In the case of random field f (x, t) delta-correlated in time, the following equality holds
(see Sect. 5.5, page 130)
˙
2
t
[t, t
0
; v( y, τ )] ≡
˙
2
t
[t, t
0
; v( y, t)],
and situation becomes significantly simpler. The fact that field f (x, t) is delta-
correlated means that
2[t, t
0
; v( y, τ )] =
∞
X
i=1
i
n
n!
t
Z
t
0
dτ
Z
dy
1
. . .
Z
dy
n
K
i
1
,...,i
n
n
( y
1
, . . . , y
n
; τ )
× v
i
1
( y
1
, τ ) . . .v
i
n
( y
n
, τ ),
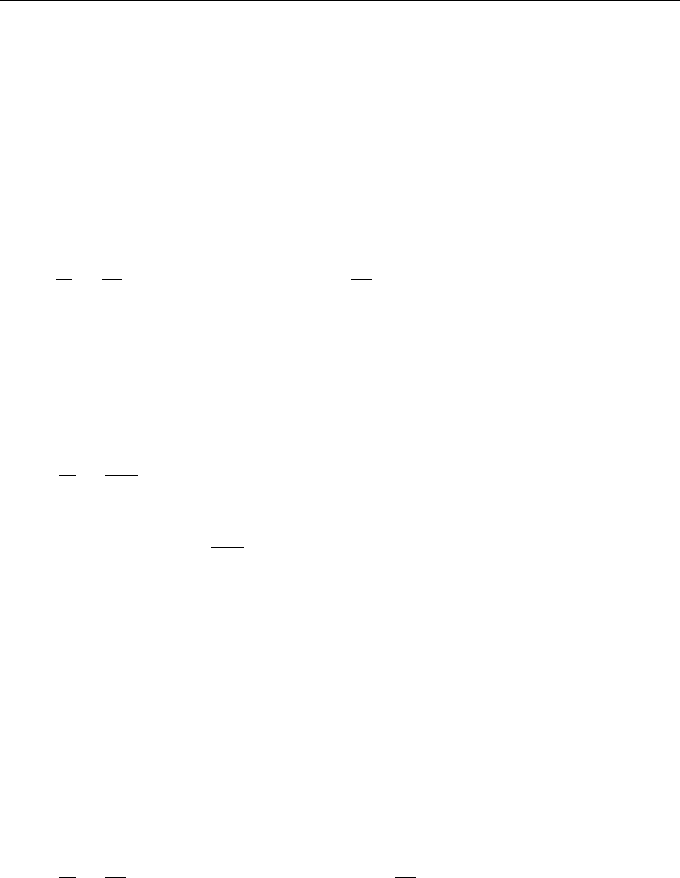
General Approaches to Analyzing Stochastic Systems 161
which, in turn, means that field f (x, t) is characterized by cumulant functions of the
form
K
i
1
,...,i
n
n
( y
1
, t
1
; . . . ; y
n
, t
n
)
= K
i
1
,...,i
n
n
( y
1
, . . . , y
n
;t
1
)δ(t
1
− t
2
) . . . δ(t
n−1
− t
n
).
In view of (6.3), page 142, Eqs. (6.7) and (6.9) appear to be in this case the closed
operator equations in functions P(x, t), p(x, t|x
0
, t
0
), and P
m
(x
1
, t
1
; . . . ; x
m
, t
m
).
Indeed, Eq. (6.7), page 143 is reduced to the equation
∂
∂t
+
∂
∂x
v(x, t)
P(x,t) =
˙
2
t
t, t
0
; i
∂
∂x
δ( y − x)
P(x, t),
P(x, 0) = δ(x − x
0
),
(6.64)
whose concrete form is governed by functional 2[t, t
0
; v( y, τ )], i.e., by statistical
behavior of random field f (x, t). Correspondingly, Eq. (6.9) for the m-time probability
density is reduced to the operator equation (t
1
≤t
2
≤ . . . ≤t
m
)
∂
∂t
+
∂
∂x
m
v(x
m
, t
m
)
P
m
(x
1
,t
1
; . . . ; x
m
, t
m
)
=
˙
2
t
m
t
m
, t
0
; i
∂
∂x
m
δ( y − x
m
)
P
m
(x
1
, t
1
; . . . ; x
m
, t
m
), (6.65)
P
m
(x
1
, t
1
; . . . ; x
m
, t
m−1
) = δ(x
m
− x
m−1
)P
m−1
(x
1
, t
1
; . . . ; x
m−1
, t
m−1)
,
We can seek the solution to Eq. (6.65) in the form
P
m
(x
1
, t
1
; . . . ; x
m
, t
m
)
= p(x
m
, t
m
|x
m−1
, t
m−1
)P
m−1
(x
1
, t
1
; . . . ; x
m−1
, t
m−1
). (6.66)
Because all differential operations in Eq. (6.65) concern only t
m
and x
m
, we can substi-
tute Eq. (6.66) in Eq. (6.65) to obtain the following equation for the transition proba-
bility density
∂
∂t
+
∂
∂x
v(x, t)
p(x, t|x
0
,t
0
) =
˙
2
t
t, t
0
; i
∂
∂x
δ( y − x)
p(x, t|x
0
, t
0
),
p(x, t|x
0
, t
0
)|
t→t
0
= δ(x − x
0
).
(6.67)
Here, we denoted variables x
m
and t
m
as x and t and variables x
m−1
and t
m−1
as x
0
and t
0
.
Using formula (6.66) (m − 1) times, we obtain the relationship
P
m
(x
1
, t
1
; . . . ; x
m
, t
m
)
= p(x
m
, t
m
|x
m−1
, t
m−1
) . . . p(x
2
, t
2
|x
1
, t
1
)P(x
1
, t
1
),
(6.68)
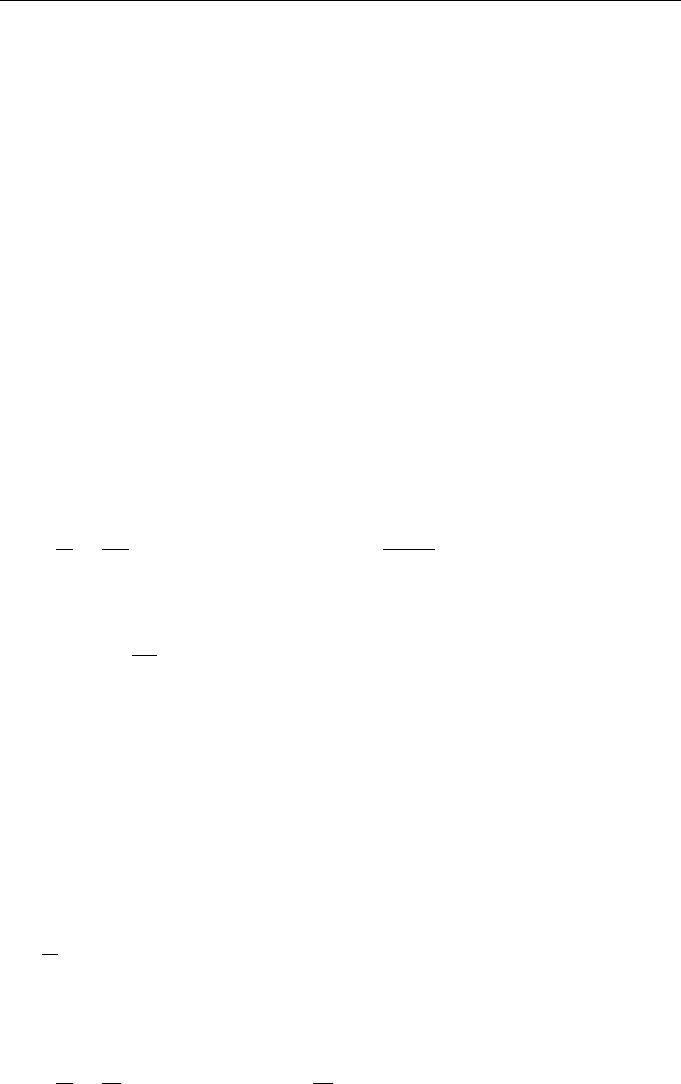
162 Lectures on Dynamics of Stochastic Systems
where P(x
1
, t
1
) is the one-time probability density governed by Eq. (6.64). Equality
(6.68) expresses the many-time probability density in terms of the product of transition
probability densities, which means that random process x(t) is the Markovian process.
The transition probability density is defined in this case as follows:
p(x, t|x
0
, t
0
) =
h
δ(x(t|x
0
, t
0
) − x)
i
.
Special models of parameter fluctuations can significantly simplify the obtained
equations.
For example, in the case of the Gaussian delta-correlated field f (x, t), the correla-
tion tensor has the form (
h
f(x, t)
i
= 0)
B
ij
(x, t; x
0
, t
0
) = 2δ(t − t
0
)F
ij
(x, x
0
; t).
Then, functional 2[t, t
0
; v( y, τ )] assumes the form
2[t, t
0
; v( y, τ )] = −
t
Z
t
0
dτ
Z
dy
1
Z
dy
2
F
ij
( y
1
, y
2
; τ )v
i
( y
1
, τ )v
j
(y
2
, τ ),
and Eq. (6.64) reduces to the Fokker–Planck equation
∂
∂t
+
∂
∂x
k
[
v
k
(x,t) + A
k
(x,t)
]
P(x, t) =
∂
2
∂x
k
∂x
l
[
F
kl
(x, x,t)P(x,t)
]
, (6.69)
where
A
k
(x, t) =
∂
∂x
0
l
F
kl
(x, x
0
;t)
x
0
=x
.
In view of the special role that the Gaussian delta-correlated field f (x, t) plays
in physics, we give an alternative and more detailed discussion of this approxima-
tion commonly called the approximation of the Gaussian delta-correlated field in
Lecture 8.
We illustrate the above general theory by the examples of several equations.
6.3.1 One-Dimensional Nonlinear Differential Equation
Consider the one-dimensional stochastic equation
d
dt
x(t) = f (x, t) + z(t)g(x, t), x(0) = x
0
, (6.70)
where f (x, t) and g(x, t) are the deterministic functions and z(t) is the random function
of time. For indicator function ϕ(x, t) = δ(x(t) − x), we have the Liouville equation
∂
∂t
+
∂
∂x
f (x, t)
ϕ(x, t) = −z(t)
∂
∂x
{
g(x, t)ϕ(x, t)
}
,
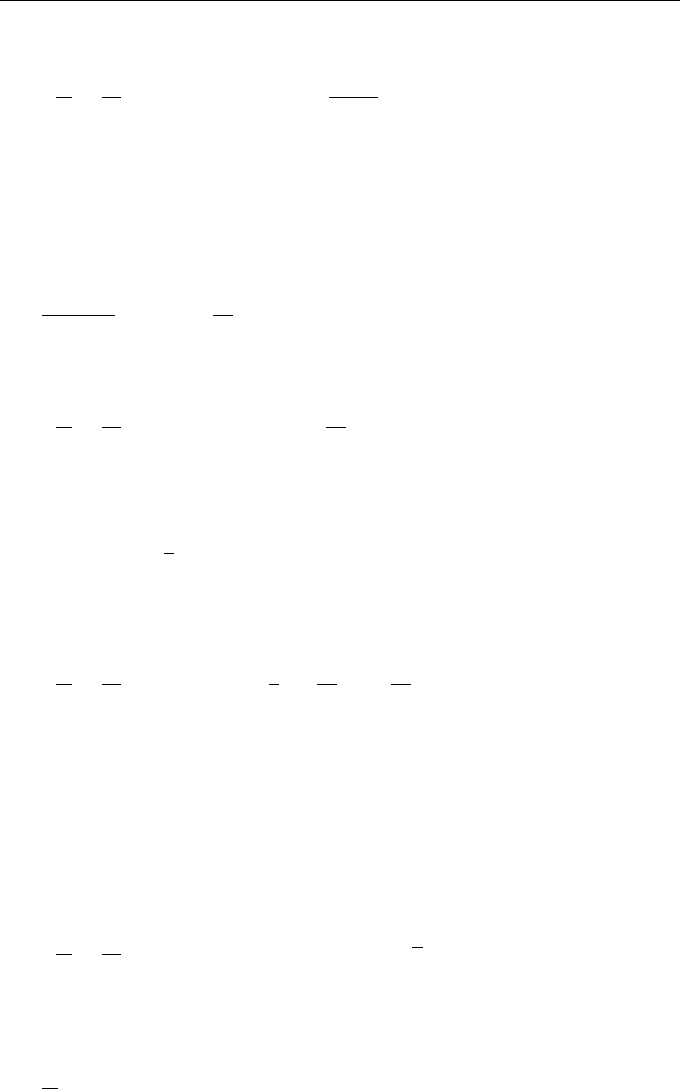
General Approaches to Analyzing Stochastic Systems 163
so that the equation for the one-time probability density P(x, t) has the form
∂
∂t
+
∂
∂x
f (x, t)
P(x, t) =
˙
2
t
t,
δ
iδz(τ )
ϕ(x, t)
.
In the case of the delta-correlated random process z(t), the equality
˙
2
t
[t, v(τ )] =
˙
2
t
[t, v(t)]
holds. Taking into account the equality
δ
δz(t − 0)
ϕ(x, t) = −
∂
∂x
{
g(x, t)ϕ(x, t)
}
,
we obtain the closed operator equation
∂
∂t
+
∂
∂x
f (x, t)
P(x, t) =
˙
2
t
t, i
∂
∂x
g(x, t)
P(x, t). (6.71)
For the Gaussian delta-correlated process, we have
2[t, v(τ )] = −
1
2
t
Z
0
dτ B(τ )v
2
(τ ), (6.72)
and Eq. (6.71) assumes the form of the Fokker–Planck equation
∂
∂t
+
∂
∂x
f (x, t)
P(x, t) =
1
2
B(t)
∂
∂x
g(x, t)
∂
∂x
g(x, t)P(x, t). (6.73)
For Poisson’s delta-correlated process z(t), we have
2[t, v(τ )] = ν
t
Z
0
dτ
∞
Z
−∞
dξp(ξ )e
iξv(τ )
− 1
, (6.74)
and Eq. (6.71) reduces to the form
∂
∂t
+
∂
∂x
f (x, t)
P(x, t) = ν
∞
Z
−∞
dξp(ξ )e
−ξ
∂
∂x
g(x,t)
−1
P(x, t). (6.75)
If we set g(x, t) = 1, Eq. (6.70) assumes the form
d
dt
x(t) = f (x, t) + z(t), x(0) = x
0
.
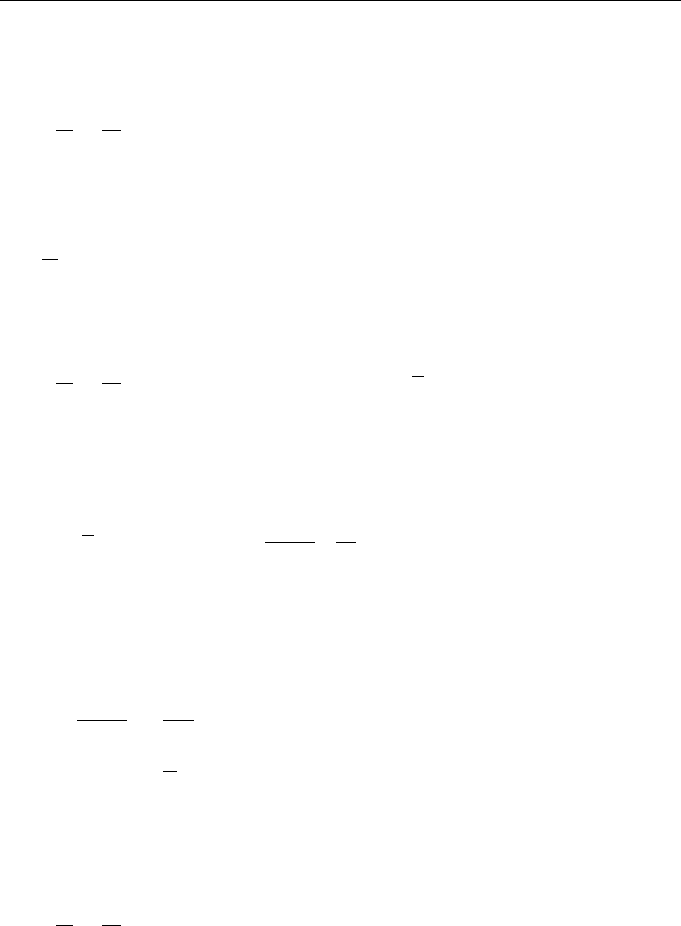
164 Lectures on Dynamics of Stochastic Systems
In this case, the operator in the right-hand side of (6.75) is the shift operator, and
Eq. (6.75) assumes the form of the Kolmogorov–Feller equation
∂
∂t
+
∂
∂x
f (x, t)
P(x, t) = ν
∞
Z
−∞
dξp(ξ )P(x − ξ, t) − νP(x, t).
Define now g(x, t) = x, so that Eq. (6.70) reduces to the form
d
dt
x(t) = f (x, t) + z(t)x(t), x(0) = x
0
.
In this case, Eq. (6.75) assumes the form
∂
∂t
+
∂
∂x
f (x, t)
P(x, t) = ν
∞
Z
−∞
dξp(ξ )e
−ξ
∂
∂x
x
−1
P(x, t). (6.76)
To determine the action of the operator in the right-hand side of Eq. (6.76), we
expand it in series in ξ
n
e
−ξ
∂
∂x
x
− 1
o
P(x, t) =
∞
X
n=1
(−ξ)
n
n!
∂
∂x
x
n
P(x, t)
and consider the action of every term.
Representing x in the form x = e
ϕ
, we can transform this formula as follows (the
fact that x is the alternating quantity is insignificant here)
∞
X
n=1
(−ξ)
n
n!
e
−ϕ
∂
n
∂ϕ
n
e
ϕ
P(e
ϕ
, t)
= e
−ϕ
n
e
−ξ
∂
∂ϕ
− 1
o
e
ϕ
P(e
ϕ
, t) = e
−ξ
P(e
ϕ−ξ
, t) − P(e
ϕ
, t).
Reverting to variable x, we can represent Eq. (6.76) in the final form of the integro-
differential equation similar to the Kolmogorov–Feller equation
∂
∂t
+
∂
∂x
f (x, t)
P(x, t) = ν
∞
Z
−∞
dξp(ξ )e
−ξ
P(xe
−ξ
, t) − νP(x, t).
In Lecture 4, page 89, we mentioned that formula
x(t) =
t
Z
0
dτ g(t − τ)z(τ )

General Approaches to Analyzing Stochastic Systems 165
relates Poisson’s process x(t) with arbitrary impulse function g(t) to Poisson’s delta-
correlated random process z(t). Let g(t) = e
−λt
. In this case, process x(t) satisfies the
stochastic differential equation
d
dt
x(t) = −λx(t) + z(t)
and, consequently, both transition probability density and one-time probability density
of this process satisfy, according to Eq. (6.75), the equations
∂
∂t
p(x, t|x
0
, t
0
) =
b
L(x)p(x, t|x
0
, t
0
),
∂
∂t
P(x, t) =
b
L(x)P(x, t),
where operator
b
L(x) = λ
∂
∂x
x + ν
∞
Z
−∞
dξp(ξ )e
−ξ
∂
∂x
− 1
. (6.77)
6.3.2 Linear Operator Equation
Consider now the linear operator equation
d
dt
x(t) =
b
A(t)x(t) + z(t)
b
B(t)x(t), x(0) = x
0
, (6.78)
where
b
A(t) and
b
B(t) are the deterministic operators (e.g., differential operators with
respect to auxiliary variables or regular matrixes). We will assume that function z(t) is
the random delta-correlated function.
Averaging system (6.78), we obtain, according to general formulas,
d
dt
h
x(t)
i
=
b
A(t)
h
x(t)
i
+
˙
2
t
t,
δ
iδz(t)
x(t)
. (6.79)
Then, taking into account the equality
δ
δz(t − 0)
x(t) =
b
B(t)x(t)
that follows immediately from Eq. (6.78), we can rewrite Eq. (6.79) in the form
d
dt
h
x(t)
i
=
b
A(t)
h
x(t)
i
+
˙
2
t
t, −i
b
B
h
x(t)
i
. (6.80)
Thus, in the case of linear system (6.78), equations for average values also are the
linear equations.
