Кирин Е.М., Базыкина Н.А., Вантеев А.Н., Краснов М.Н. Построение сечений и линий пересечения поверхностей

Подождите немного. Документ загружается.

а – метод вспомогательных плоскостей;

б – метод вспомогательных концентрических сфер

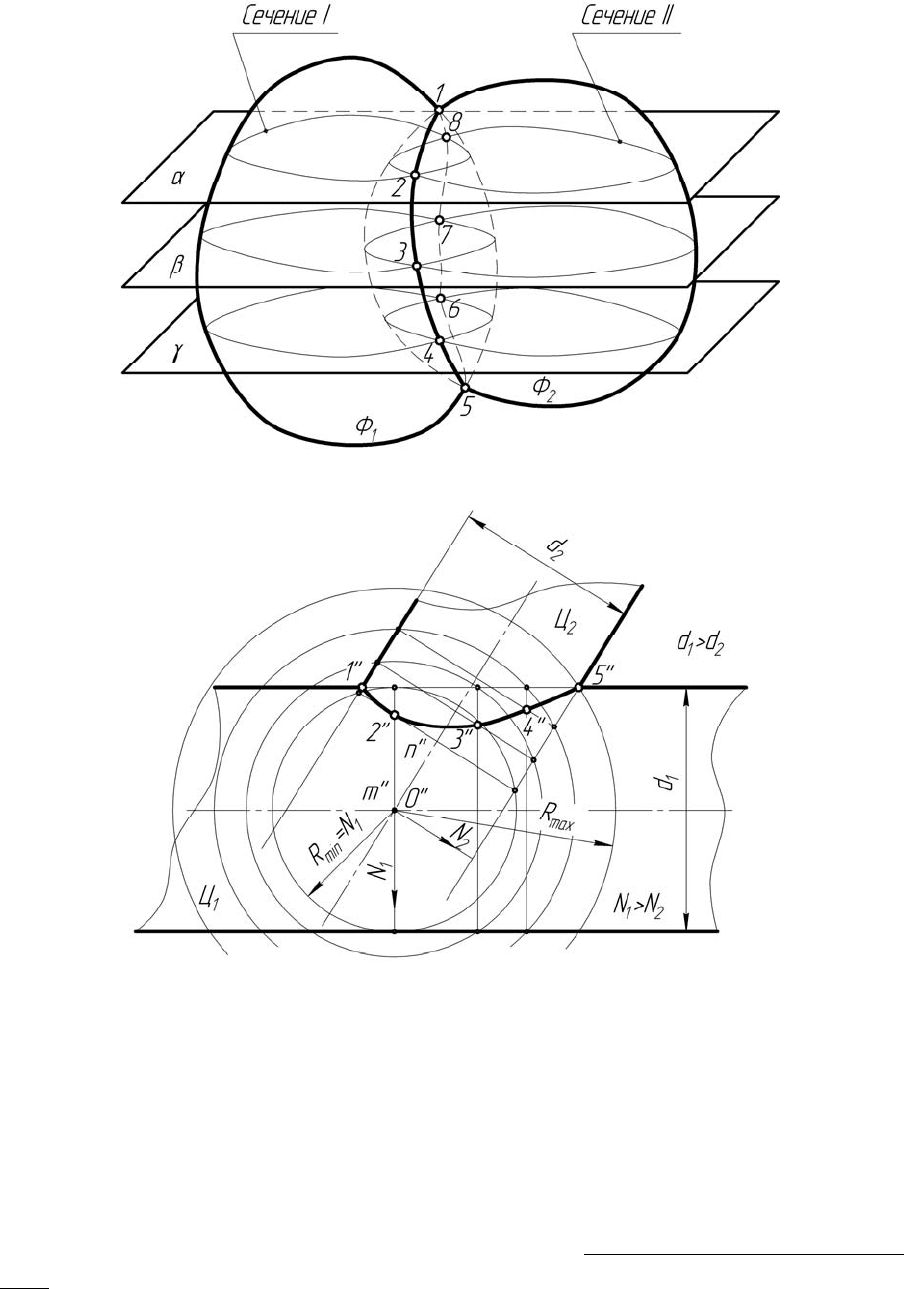
Рисунок 6.7 – Основные методы построения линии пересечения

поверхностей

- пересекаем обе поверхности вспомогательной плоскостью a.

Вспомогательные плоскости подбираем по «принципу простых сече-

ний» так, чтобы в сечениях обеих поверхностей вспомогательной

плоскостью получились простые фигуры;

- строим сечения обеих поверхностей вспомогательной плоско-

стью: a

Þ сечение I; a

Þ сечение II;

а)

б)

- находим общие точки сечений I и II. Сечение I

сечение II Þ

точки 2 и 8;

- повторяем операции с вспомогательными плоскостями b, g и др.

Совокупность всех параллельных вспомогательных плоскостей назы-

вают семейством

;

- соединяем полученные точки плавной линией с учетом види-

мости.

На рисунке 6.8 представлен пример использования метода

вспомогательных плоскостей для построения линии пересечения

призмы со сферой.

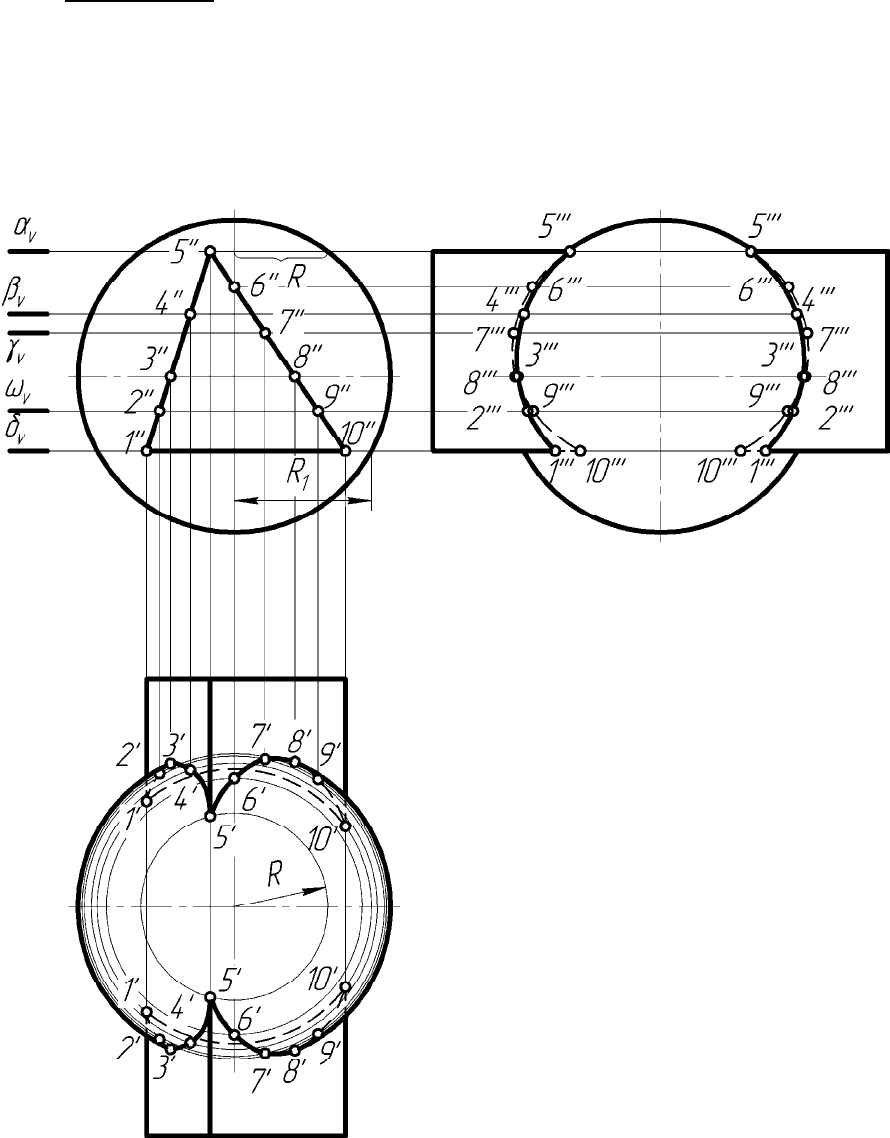
Рисунок 6.8 – Построение линии пересечения трехгранной призмы

со сферой методом вспомогательных плоскостей

В качестве вспомогательных плоскостей взяты горизонтальные

плоскости, так как они образуют в сечениях на горизонтальной про-

екции прямые линии (сечения призмы) и окружности известного ра-

диуса (сечения сферы). Характерные точки – 3

, 6

, 8

. В этих точках

линия пересечения касается образующей линии, в этих же точках про-

исходит смена видимости.

Предварительный анализ показывает, что линия пересечения со-

стоит из трех участков (по числу граней призмы). Нижний участок

будет являться частью окружности, боковые участки – частями эл-

липсов. Ход построений:

- находим проекции характерных точек 3, 6, 8;

- вводим вспомогательную горизонтальную плоскость a;

- строим сечение сферы (окружность радиуса R);

- строим сечение призмы (прямая линия);

- находим общие точки сечений (две точки 5

);

- повторяем аналогичные построения для остальных точек;

- соединяем все точки плавной линией в следующем порядке:

1–2–3–4–5; 5–6–7–8–9–10; 1–10 по окружности с радиусом R

;

- определяем видимость участков линии пересечения.

На рисунке 6.9 представлено решение задачи на построение ли-

ний среза, образующихся на поверхности вращения, если ее срезать

одной или двумя плоскостями (например фрезерованием) вдоль оси

поверхности.

Задача решена методом вспомогательных плоскостей (профиль-

ных). После проведения плоскости на профильной проекции детали

строят окружность сечения. Далее отмечают точки пересечения этой

окружности с плоскостью среза. Полученные точки возвращают на

вспомогательную плоскость.

Характерные точки – 1

, 8

, 5

///

, 6

///

;

вспомогательные профильные плоскости – a, b, g, w

Рисунок 6.9 – Построение линии среза поверхности вращения

методом вспомогательных плоскостей

6.5 Метод вспомогательных концентрических сфер

Метод вспомогательных концентрических сфер основан на ча-

стном случае пересечения поверхностей со сферой (см. рисунок 6.4,г).

Метод заключается в том, что вместо вспомогательных плоскостей

заданные поверхности пересекаются сферами. В остальном же метод

сфер реализуется так же, как и метод вспомогательных плоскостей.

Метод вспомогательных сфер можно применять при следующих

условиях:

- обе поверхности должны быть поверхностями вращения;

- оси поверхностей должны пересекаться между собой;

- оси поверхностей должны быть параллельны одной из плос-

костей проекций.

Схема реализации метода вспомогательных концентрических

сфер показана на рисунке 6.7,б:

- по размерам диаметров цилиндров определяем, что цилиндр

будет врезаться в цилиндр Ц

;

- находим характерные точки 1 и 5;

- на пересечении осей поверхностей находим центр сфер О;

- из центра сфер О опускаем на боковые поверхности цилинд-

ров нормали N

и N

;

- сравниваем N

и N

, определяем, что N

> N

;

- берем N

за минимальный радиус сферы (R

min

= N

);

- определяем максимальный радиус сферы. Он равен расстоя-

нию от центра сфер О до наиболее удаленной характерной точки 5;

- проводим сферу с радиусом R

min

;

- определяем линии пересечения сферы с цилиндрами (линии n

и m

);

- находим общую точку линий n

и m

(точка 2

);

- увеличиваем радиус сферы и повторяем построения. Получа-

ем точки 3

и 4

;

- полученные точки соединяем плавной линией с учетом види-

мости.

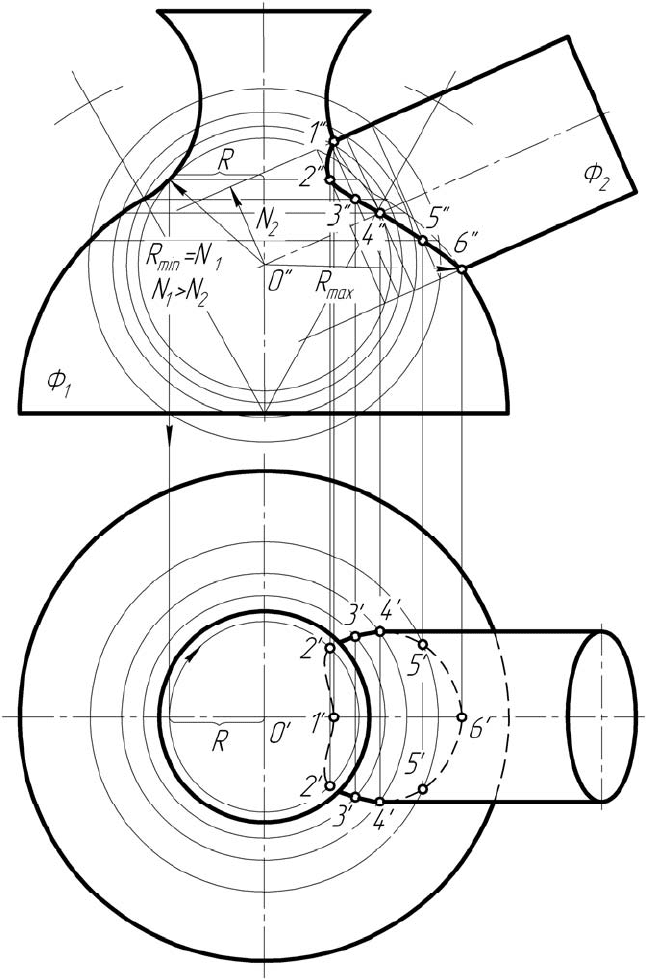
На рисунке 6.10 показано построение линии пересечения тора с

наклонным цилиндром. Ход построения ясен из рисунка.

Рисунок 6.10 – Построение линии пересечения цилиндра

и тора методом концентрических сфер

6.6 Метод вспомогательных эксцентрических сфер

Метод заключается в использовании сфер, имеющих различные

центры. Введением эксцентрических сфер область применения мето-

да сфер значительно расширяется.

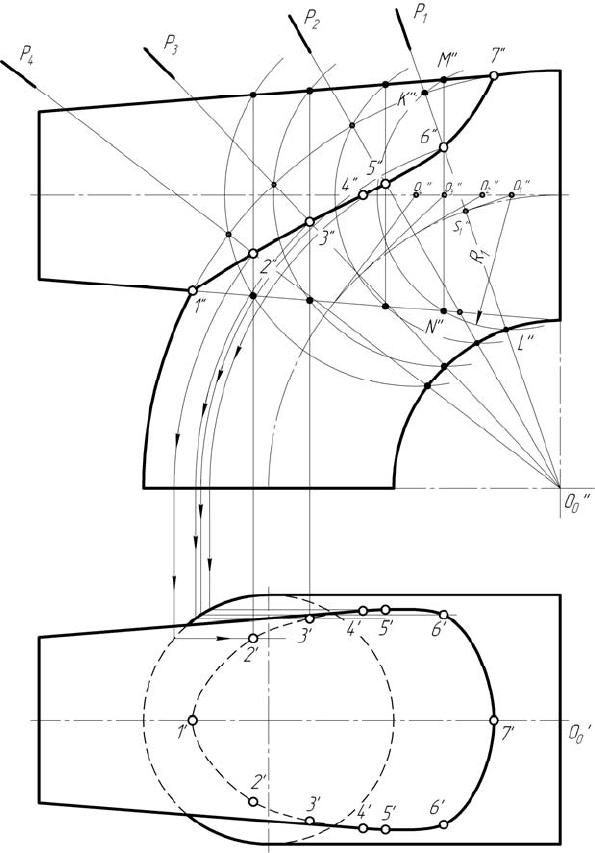
Рассмотрим использование данного метода на примере пересе-

чения конуса с торовым кольцом (рисунок 6.11).

1) Характерные точки – 1, 4, 7.

2) Центры вспомогательных сфер – О

– О

3) Радиусы вспомогательных сфер – R

– R

4) Промежуточные точки – 2, 3, 5, 6.

Рисунок 6.11 – Построение линии пересечения тора

и конуса методом эксцентрических сфер

Конус лежит в плоскости средней линии торового кольца, т.е. у

поверхностей есть общая плоскость симметрии. Ход решения задачи:

- находим характерные точки 1

и 7

;

- для построения промежуточных точек через ось кольца О

проведем фронтально-проецирующую плоскость Р

. Она рассекает

тор по окружности с центром S

;

- из центра S

проведем касательную к оси тора до пересечения

с осью конуса в точке О

;

- принимаем точку О

за центр вспомогательной сферы. Радиус

сферы подбираем так, чтобы окружность сферы прошла через точ-

ки K

и L

;

- находим линию пересечения этой сферы с конусом (линия

);

- находим общую точку линий Р

и M

– точка 6

;

- проводим плоскости Р

, Р

и Р

и повторяем построения. На-

ходим точки 5

, 3

, 2

. Точку 4 находим как характерную после об-

водки линии;

- горизонтальные проекции точек 5, 3, 2, 6 находим с помощью

фронталей f (или вращением).

6.7 Построение линий пересечения поверхностей

с помощью вспомогательных плоскостей

общего положения

В некоторых случаях использование вспомогательных плоско-

стей частного положения не позволяет получить простые сечения, ес-

ли поверхности, например, эллиптические, торовые, параболические

или наклонные и т.д. В этом случае более удобными являются вспо-

могательные плоскости общего положения. Такими удобными вспо-

могательными плоскостями для конуса являются плоскости, прохо-

дящие через вершину S, а для цилиндра – плоскости, проходящие па-

раллельно оси цилиндра. В первом случае в сечении получается тре-

угольник, во втором – прямоугольник или параллелограмм.

Используем это для построения линии пересечения поверх-

ностей.

На рисунке 6.12 приведен пример использования вспомогатель-

ных плоскостей общего положения для определения линии пересече-

ния двух конусов с пересекающимися осями. Ход решения задачи вы-

текает из общего метода решения задач с использованием вспомога-

тельных плоскостей, но имеет некоторые особенности:

- находим характерные точки – 1 и 8 как точки пересечения ос-

нований конусов;

- соединяем вершины S

и S

конусов прямой линией;

- найдем горизонтальный след H

этой линии;

- через точку H

будем проводить вспомогательные секущие

плоскости Р

– Р

, являющиеся плоскостями общего положения. Эти

плоскости будут проходить через прямую S

(она называется собст-

венной прямой) и будет пересекать основания конусов в некоторых

точках, соединив которые с вершинами S

и S

, получим в сечении

треугольники;

1) Характерные точки – 1, 8.

2) Промежуточные точки – 2, 3, 4, 5, 6, 7

(находятся с помощью пучка плоскостей Р

– Р

Рисунок 6.12 – Построение линии пересечения двух конусов

с использованием пучка вспомогательных плоскостей

- вспомогательная плоскость, например Р

пересекает основа-

ния конуса К

в точках М

и N

, а основание конуса К

в точке L

;

- соединим точки М

, M

, N

, L

с вершинами S

, S

и получим треугольники сечения;

- находим общую точку этих сечений – это точка 5. От плоско-

сти Р

получилась только одна точка, так как плоскость Р

была про-

ведена касательно к основанию конуса К

;

- проводим плоскости Р

, Р

и повторяем построения анало-

гично описанному. В результате получим точки 2, 3, 4, 6, 7, соединив

которые плавной линией, построим проекции линии пересечения.

Нетрудно заметить, что вспомогательные плоскости проходят

через прямую S

в виде пучка (иногда эти плоскости называют вра-

щающимися плоскостями).

Рассмотрим задачу о пересечении наклонных цилиндров (рису-

нок 6.13). Решение этой задачи не отличается от предыдущей, так как

цилиндрическую поверхность можно рассматривать как частный слу-

чай конической поверхности с вершиной в несобственной точке.

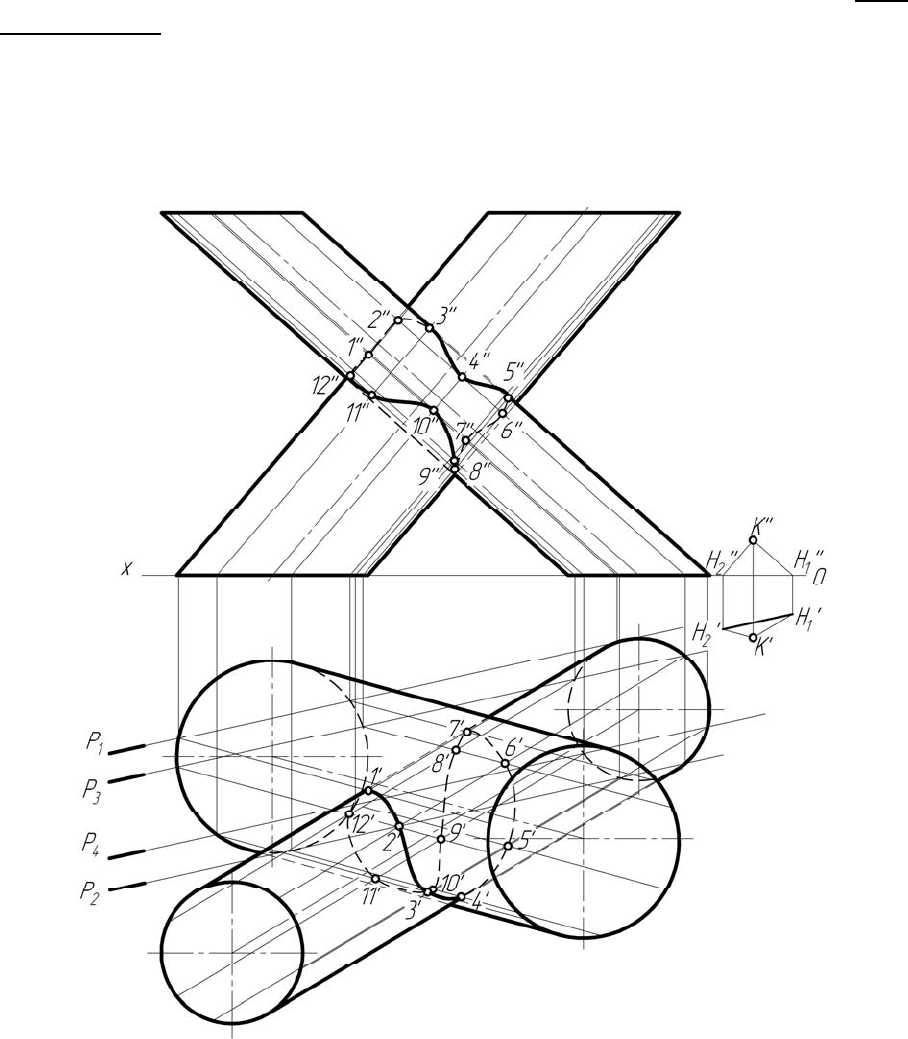
Рисунок 6.13 – Построение линии пересечения двух цилиндров

с помощью связки плоскостей, проходящих через несобственную точку