Кирин Е.М., Базыкина Н.А., Вантеев А.Н., Краснов М.Н. Построение сечений и линий пересечения поверхностей

Подождите немного. Документ загружается.

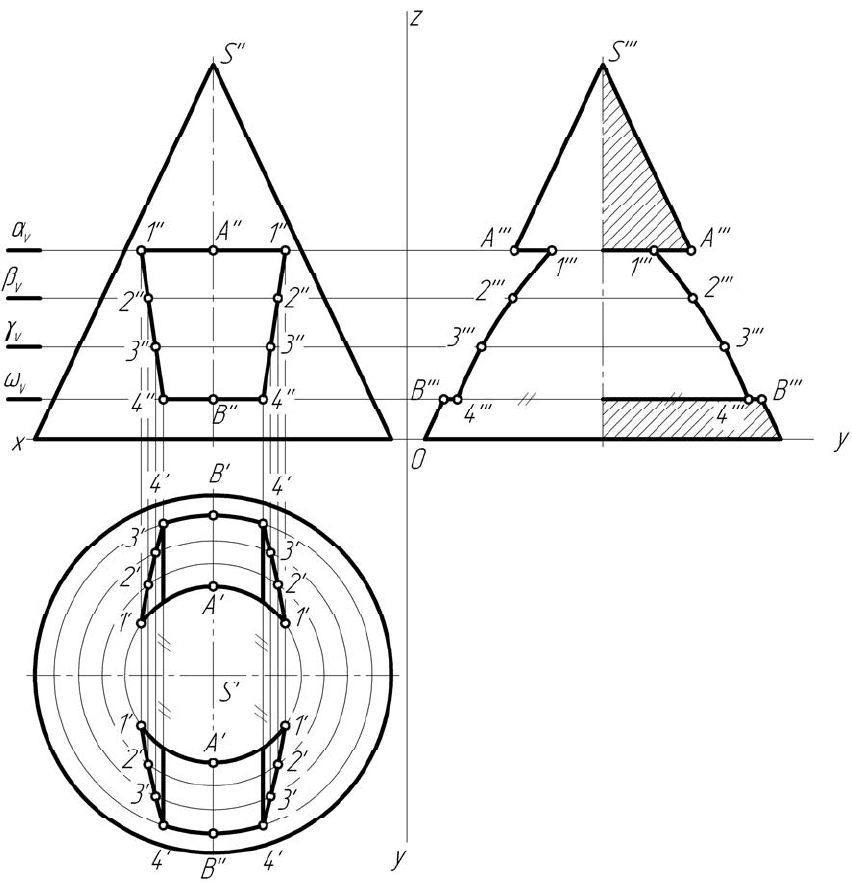
Рисунок 5.6 – Построение проекций тела вращения

с поперечным сквозным призматическим пазом

Задача о построении проекций тела вращения с поперечным па-

зом имеет свои особенности, заключающиеся в том, что число харак-

терных точек сокращается, а те точки, которые есть, практически не

участвуют в построении сечений. В данном примере такими точками

являются точки А и В.

Задача решается методом вспомогательных секущих плоско-

стей, рассмотренных ранее. В качестве вспомогательных плоскостей

использованы горизонтальные плоскости a, b, g и w.

На профильной проекции построен простой вертикальный про-

фильный разрез конуса с тем, чтобы показать сквозной поперечный

паз, выполненный в конусе.

6 Взаимное пересечение поверхностей

6.1 Общие положения

Две поверхности, взаимодействуя друг с другом, пересекаются

по линии пересечения, которая трактуется как линия, общая для обе-

их пересекающихся поверхностей.

Построение линии пересечения технических форм на производ-

ственных чертежах является важнейшей конструкторской задачей.

Не менее важной задачей является разметка линий пересечения на по-

верхности технических форм перед их сборкой, сваркой, пайкой и т.д.

Особенно часто эти практические задачи встречаются при изготовле-

нии трубопроводов и их ремонте.

Из курса начертательной геометрии известно много способов

построения линии пересечения поверхностей. На рисунке 6.1 при-

ведена классификация известных методов построения линий пере-

сечения.

Наиболее общим и универсальным способом построения линии

пересечения поверхностей является способ вспомогательных секущих

поверхностей (посредников). Он заключается в том, что пересекаю-

щиеся поверхности Ф

и Ф

рассекают вспомогательной поверхно-

стью Ф

, строят сечения I и II поверхностей вспомогательной поверх-

ностью, далее находят общие точки А и В этих сечений. Найденные

точки являются точками линии пересечения (ЛП). Если провести дос-

таточное количество вспомогательных секущих поверхностей, то по-

лучится соответственно достаточное количество точек, с определен-

ной степенью точности определяющих линию пересечения поверхно-

стей (рисунок 6.2).

Поверхности-посредники могут быть плоскими

и кривыми.

В большинстве случаев используются плоские посредники – метод

вспомогательных секущих плоскостей. В качестве вспомогательных

плоскостей могут быть использованы плоскости частного и общего

положения. Вспомогательные плоскости-посредники, как правило,

проводятся семействами

параллельных плоскостей. Вспомогательные

плоскости общего положения могут быть проведены как семейством,

так и пучком плоскостей

. В любом случае семейство или пучок плос-

костей называют связкой

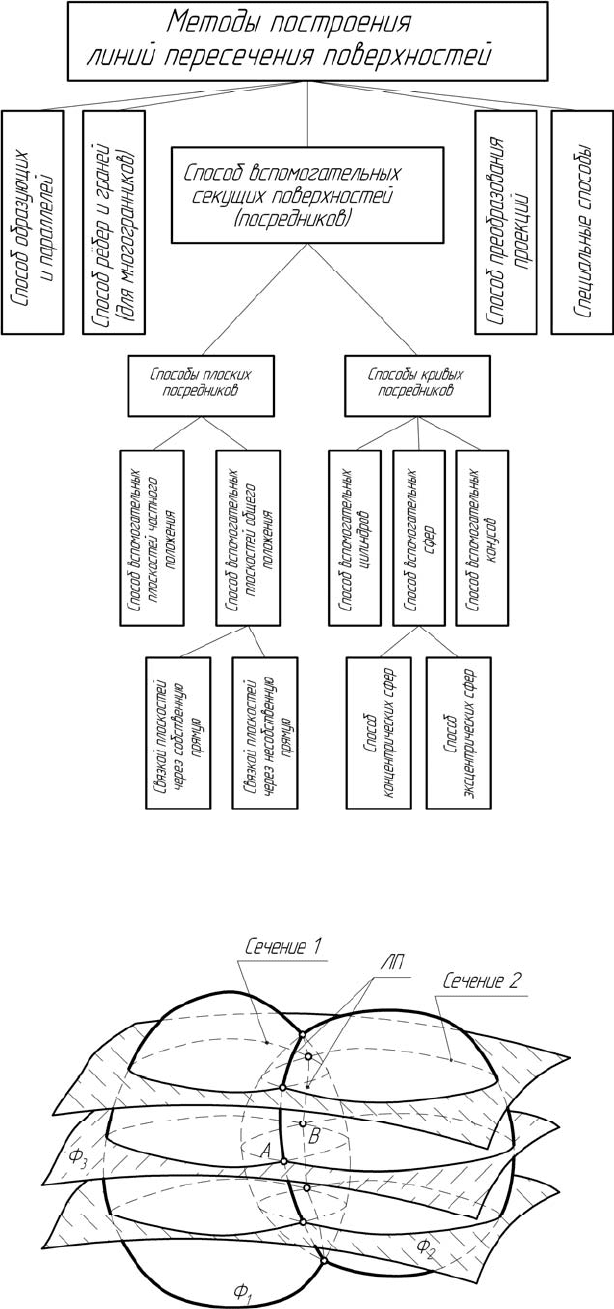
Рисунок 6.1 – Классификация основных графических методов

построения линий пересечения поверхностей

Рисунок 6.2 – Построение линии пересечения поверхностей способом

вспомогательных секущих поверхностей-посредников

Пучок плоскостей может быть проведен через собственную пря-

мую, например, через прямую, соединяющую вершины двух пересе-

кающихся конусов. Иногда пучок плоскостей проводят через несоб-

ственную прямую (находящуюся в бесконечности), например, в слу-

чае, если пересекаются два наклонных цилиндра.

В качестве кривых посредников

могут быть использованы сфе-

ры, конусы и цилиндры. Наиболее распространены сферы. Существу-

ет два способа вспомогательных секущих сфер:

способ концентриче-

ских сфер (с постоянным центром сфер) и способ эксцентрических

сфер (с переменным центром сфер).

Менее распространенными методами построения линий пересе-

чения поверхностей являются: способ образующих и параллелей и

способ преобразования проекций.

В первом способе точки линий пересечения находятся с помо-

щью образующих и параллелей, проводимых на пересекающихся по-

верхностях. Однако во многих случаях это сделать достаточно сложно.

Во втором способе пересекающиеся поверхности (чаще всего

одну из них) переводят в частное положение, используя методы пре-

образования эпюра Монжа, что позволяет упростить решение задачи.

Для решения некоторых графических и практических задач раз-

работаны специальные методы (способ двойных следов, метод проек-

тивной геометрии, аффинные преобразования и т.д.). В учебной рабо-

те специальные методы практически не используются.

6.2 Частные случаи пересечения поверхностей

В самом общем виде поверхности пересекаются между собой по

четырем возможным вариантам (рисунок 6.3):

1) полное пересечение (полное проницание) – все образующие

одной поверхности пересекаются со второй поверхностью. В этом

случае взаимная линия пересечения распадается на две или больше

кривых линий (рисунок 6.3,б);

2) неполное пересечение (частичное врезание) – часть образую-

щих одной поверхности не пересекается со второй поверхностью.

В этом случае линия пересечения представляет собой замкнутую про-

странственную кривую линию (рисунок 6.3,а);

3) одностороннее соприкасание – пересекающиеся поверхно-

сти имеют в одной точке общую плоскость касания. Линия пересе-

чения в этом случае имеет точку самопересечения в точке касания

(рисунок 6.3,в);

4) двойное соприкосновение – пересекающиеся поверхности

имеют две точки касания (две плоскости касания). В этом случае ли-

ния пересечения распадается на две плоские кривые линии, пересе-

кающиеся между собой в точках касания (рисунок 6.3,г).

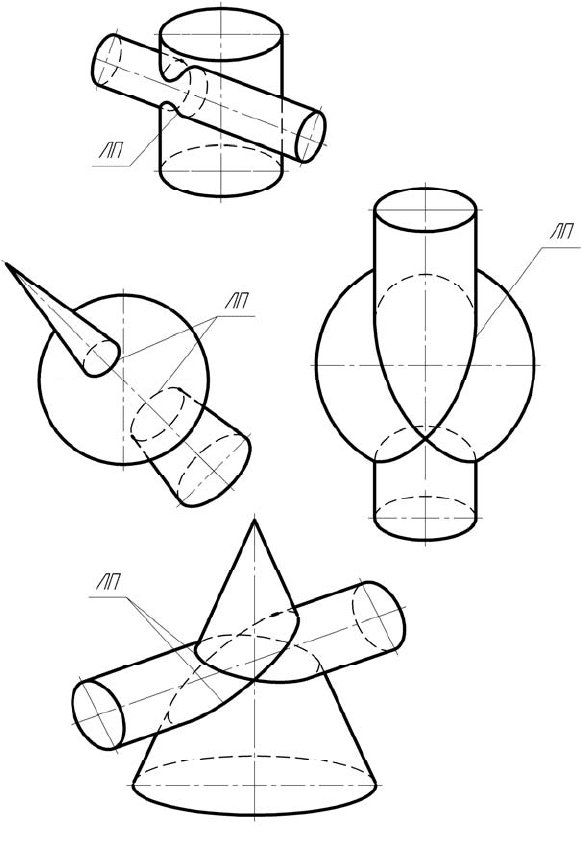
а – неполное пересечение; б – полное пересечение;

в – одностороннее соприкосновение; г – двойное соприкосновение

Рисунок 6.3 – Возможные случаи пересечения кривых поверхностей

Существуют также частные случаи пересечения поверхностей.

Так, например, две цилиндрические поверхности с параллельными

осями пересекаются по прямым линиям, соединяющим точки пересе-

чения оснований цилиндров (рисунок 6.4,а).

а)

б)

в)

г)

Две конические поверхности с общей вершиной пересекаются

по прямым линиям, соединяющим вершину и точки пересечения ос-

нований (рисунок 6.4,б).

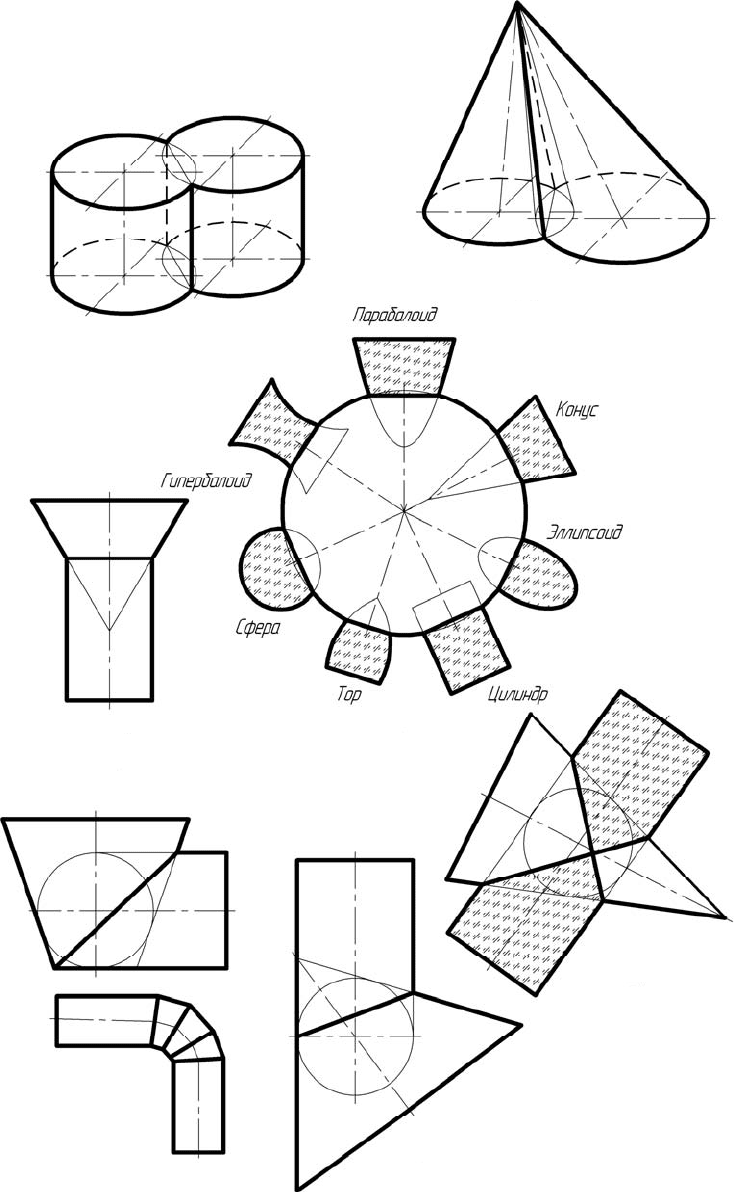
Рисунок 6.4 – Частные случаи пересечения поверхностей

а)

б)

в)

г)

д)

е)

Две соосные поверхности вращения (соосными называются по-

верхности с совпадающими осями) пересекаются по окружностям,

число которых равно числу точек пересечения образующих линий по-

верхностей, расположенных в одной меридиональной плоскости и по

одну сторону от оси вращения (рисунок 6.4,в). На фронтальной про-

екции окружности «вырождаются» в прямые линии, соединяющие

характерные соседние точки.

Частный случай пересечения поверхностей вращения со сферой

(рисунок 6.4,г) имеет особое значение, так как на нем основан метод

вспомогательных сфер, используемый при построении линии пересе-

чения двух поверхностей.

Соосные со сферой поверхности вращения пересекаются по ок-

ружностям, проекции которых на плоскость, параллельную оси вра-

щения, «вырождаются» в прямые линии, так как плоскости этих ок-

ружностей перпендикулярны к плоскостям проекций. Окружности

пересечения проецируются на плоскость, параллельную оси враще-

ния, в прямую линию, а на плоскость, перпендикулярную к оси вра-

щения, – в натуральную величину.

Если две поверхности вращения второго порядка описаны во-

круг одной и той же сферы, то они пересекаются по двум плоским

кривым линиям второго порядка, фронтальная проекция которых

«вырождается» в прямые линии, соединяющие противоположные ха-

рактерные точки (рисунок 6.4,д). Эта закономерность называется тео-

ремой Монжа для пересекающихся поверхностей.

На рисунке 6.4,е представлены некоторые примеры конструиро-

вания переходов труб с пересекающимися осями, что очень важно при

изготовлении и ремонте трубопроводов. Из рисунка видно, что линии

пересечения патрубков на проекциях «вырождены» в прямые линии.

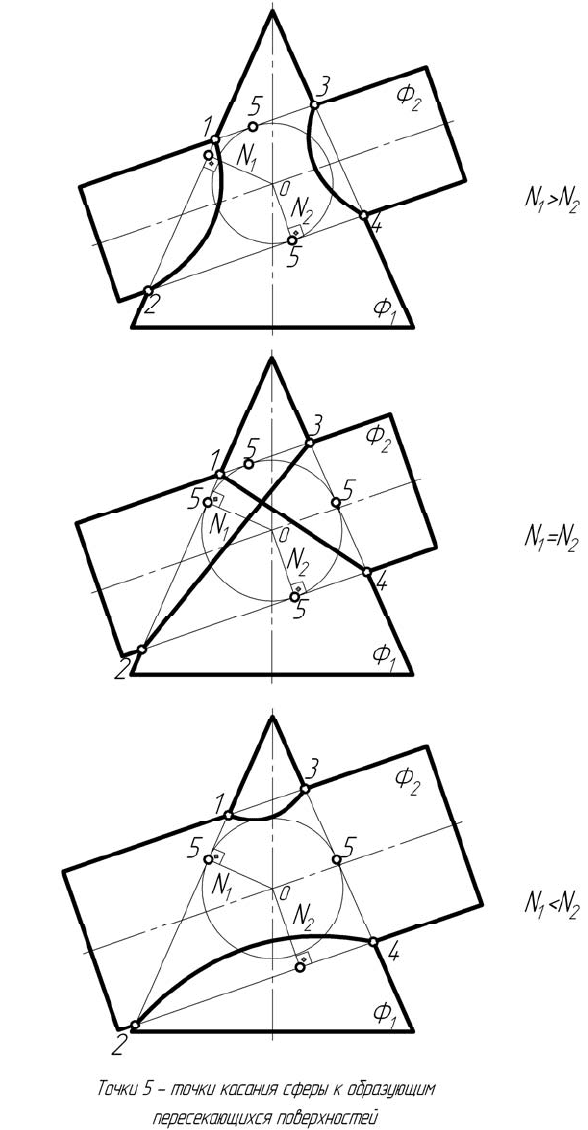
При построении линии пересечения поверхностей вращения с

пересекающимися осями целесообразно предварительно проанализи-

ровать поверхности на их «толщину», которую можно оценить величи-

ной нормалей N, проведенных из точки О пересечения осей на боковые

поверхности. Нормаль – это перпендикуляр, проведенный из центра О

на боковые поверхности пересекающихся фигур (рисунок 6.5). Поверх-

ность с меньшей нормалью всегда «врезается» в поверхность с боль-

шей нормалью. Если N

= N

, то происходит двойное соприкоснове-

ние поверхностей по теореме Монжа.

На рисунке 6.5,а показан случай, когда нормаль N

конуса боль-

ше нормали N

цилиндра. При таком соотношении нормалей цилиндр

«врезается» в конус и линия пересечения распадается на две линии.

На рисунке 6.5,б представлено двойное соприкосновение конуса

и цилиндра, когда их нормали одинаковы по величине. На фронталь-

ной проекции линии пересечения «вырождаются» в прямые линии,

соединяющие противоположные характерные точки.

Рисунок 6.5 – Три возможных вида пересечения поверхностей вращения

с пересекающимися осями

а)

б)

в)

Если нормаль N

конуса меньше нормали N

цилиндра, то конус

«врезается» в цилиндр и линия пересечения также распадается на две

линии (рисунок 6.5,в).

6.3 Построение линии пересечения поверхностей

методом образующих и параллелей

В соответствии с разд. 5.1 «Точка на поверхности» образующие

линии и параллели поверхностей вращения могут быть использованы

как вспомогательные линии для построения проекций точек на по-

верхности.

В связи с этим положением их можно использовать и для по-

строения линии пересечения поверхностей. Такой способ называется

методом образующих и параллелей.

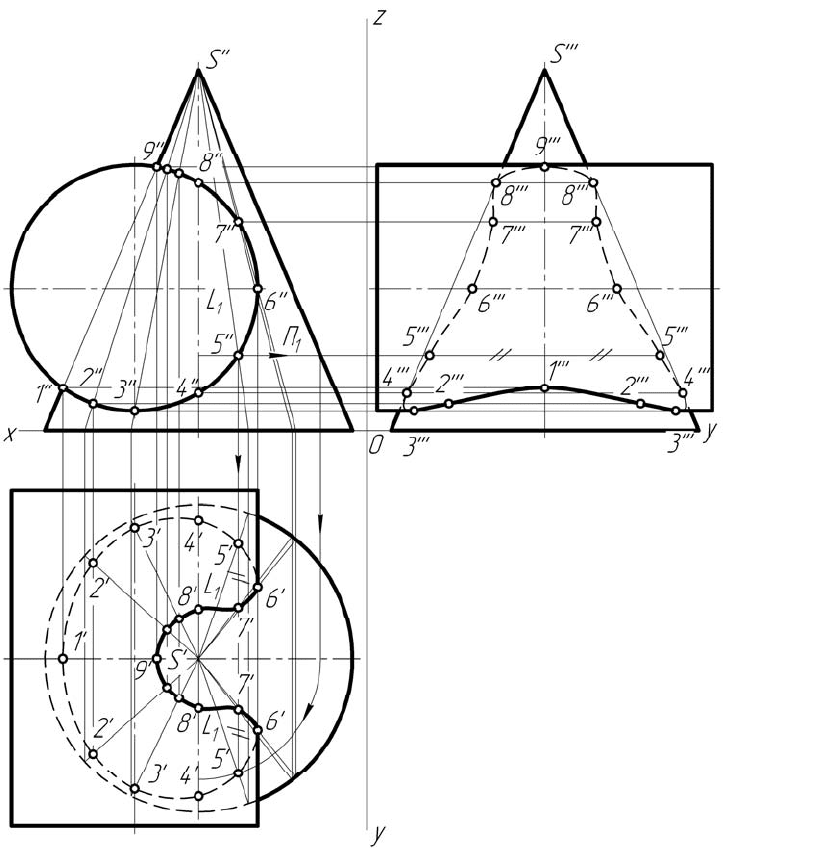
Пример использования этого метода показан на рисунке 6.6.

В примере пересекаются конус и цилиндр с пересекающимися осями,

но в частном положении. Задача решается в следующем порядке:

- находим характерные точки 1 и 9 как точки пересечения обра-

зующих линий. Находим также характерные точки 8 и 4, лежащие на

оси конуса. Строим проекции упомянутых точек;

- намечаем на фронтальной проекции цилиндра промежуточ-

ные точки 2, 3, 5, 6, 7. На окружности цилиндра (фронтальная проек-

ция цилиндра) будут находиться все точки линии пересечения, так

как поверхность цилиндра фронтально-проецирующая;

- проводим через все намеченные фронтальные проекции точек

фронтальные проекции образующих конуса и находим их на горизон-

тальной проекции;

- по линиям связи находим горизонтальные проекции точек

2…7 на горизонтальных проекциях образующих;

- профильные проекции данных точек находим, используя

свойство эпюра Монжа (А

=А

///

);

- соединяем плавной линией все полученные точки;

- определяем видимость проекций линии пересечения. На гори-

зонтальной проекции будут видны точки, лежащие выше оси цилинд-

ра, т.е. точки 9, 8, 7, 6. В точке 6 происходит смена видимости.

На профильной проекции будут видны точки, лежащие левее верти-

кальной оси цилиндра. Это точки 1, 2, 3. В точках 3 видимость ме-

няется.

В этой задаче вместо образующих можно использовать паралле-

ли. На рисунке 6.6 проекции точки 5 найдены как с помощью обра-

зующей L

, так и с помощью параллели П

Рисунок 6.6 – Построение линии пересечения конуса

и цилиндра методом образующих

6.4 Метод вспомогательных секущих плоскостей

Общая схема метода вспомогательных плоскостей показана на

рисунке 6.7,а. Метод реализуется в следующем порядке:

- находим характерные точки 1 и 5 (точки пересечения обра-

зующих линий обеих поверхностей, если оси поверхностей пересе-

каются);

1) Характерные точки

–

2) Высшая точка – 9, низшая – 3.

3) Точки смены видимости – 6.