Кирин Е.М., Базыкина Н.А., Вантеев А.Н., Краснов М.Н. Построение сечений и линий пересечения поверхностей
Подождите немного. Документ загружается.

10
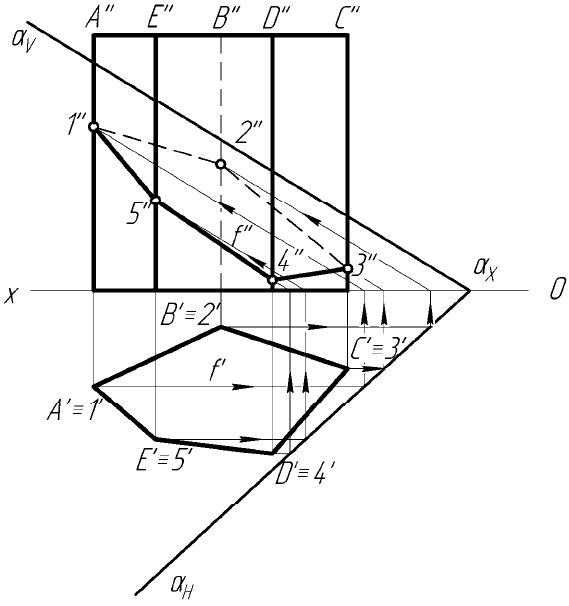
Однако если многогранник находится в частном положении
(рисунок 2.3), то задачу можно решить упрощенным способом.
В примере призма является горизонтально-проецирующей. Ее ребра
перпендикулярны горизонтальной плоскости проекций и на горизон-
тальной плоскости проекций «вырождаются» в точки, в которых на-
ходятся также точки сечения 1–2–3–4–5–1. Так как точки 1–5 принад-
лежат секущей плоскости, то их фронтальные проекции могут быть
найдены с помощью прямых, принадлежащих данной плоскости, на-
пример фронталей.
Рисунок 2.3 – Построение сечения призмы плоскостью
общего положения с помощью фронталей
На рисунке 2.4 представлена задача о построении сечения мно-
гогранника (пирамиды), когда многогранник и секущая плоскость яв-
ляются объектами общего положения. Задача решается следующим
образом:
- находим точки 1, 2, в которых горизонтальный след плоскости
a пересекается с основанием пирамиды АВС (основание АВС и a
Н
на-
ходятся в одной плоскости Н и поэтому пересекутся в точках 1 и 2);
- намечаем задачи на пересечение ребер с секущей плоскостью:
SC
Ç
a, SB
Ç
a, SA
Ç
a;
11
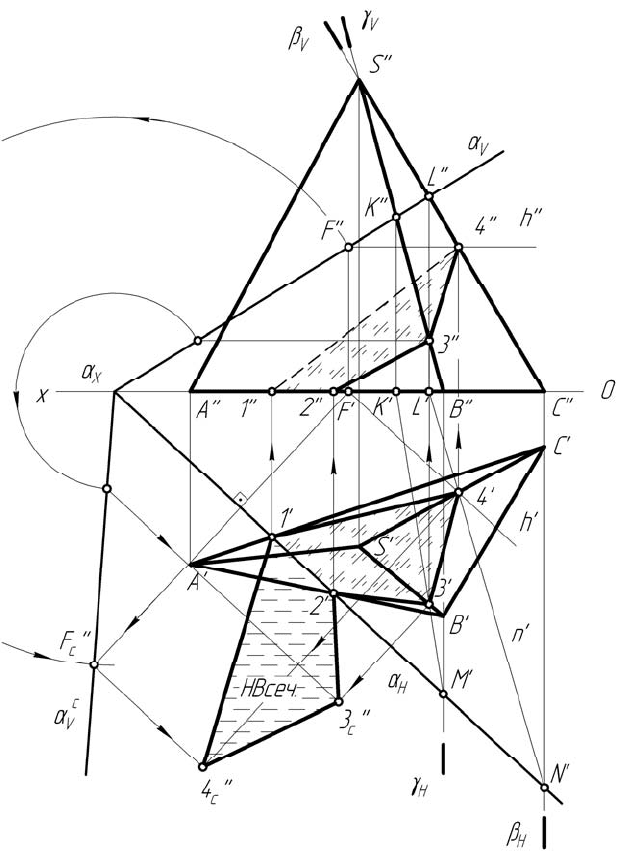
Рисунок 2.4 – Построение сечения пирамиды плоскостью общего
положения (методом ребер) и определение натуральной величины
сечения (методом совмещения)
- решаем задачу SC
Ç
a. Через SC проводим вспомогательную
плоскость b, строим линию пересечения плоскостей a и b (прямая LN),
находим точку пересечения LN с ребром SC (точка 4);
- аналогично решаем задачу SB
Ç
a. Находим точку 3;
- при решении SA
Ç
a получается, что ребро SA с секущей плос-
костью не пересекается в пределах многогранника;
- полученные точки соединяем прямыми линиями с учетом их
видимости;
- определяем натуральную величину (НВ) сечения методом со-
вмещения (вращением сечения вокруг горизонтального следа плоско-
сти a).
12
3 Построение линии пересечения
многогранников
Линия, общая для пересекающихся поверхностей, называется
линией пересечения. Линия пересечения двух многогранников мо-
жет быть плоской и пространственной, замкнутой или распадающейся
на две линии. Иногда линия пересечения может быть незамкнутой.
Вид линии пересечения определяется характером пересечения.
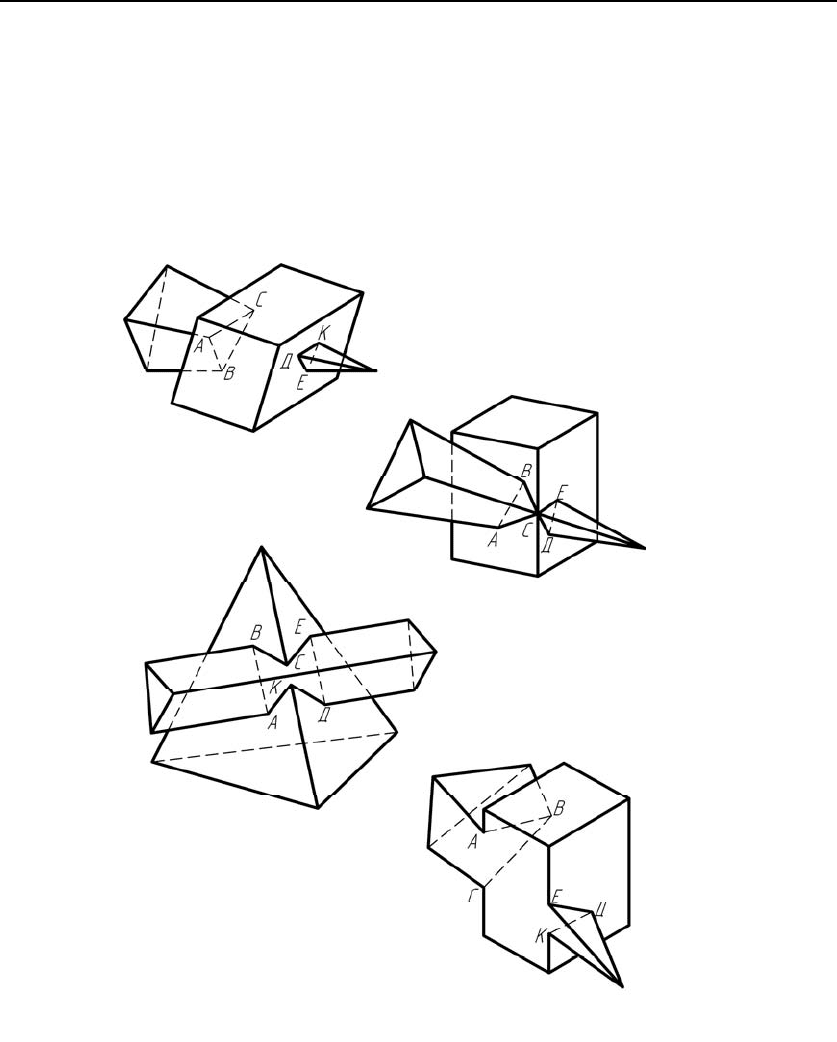
На рисунке 3.1 представлены возможные случаи пересечения много-
гранников.
а – полное; б – полное с касанием ребер; в – неполное;
г – полное с касанием граней
Рисунок 3.1 – Возможные случаи пересечения многогранников
а)
б)
в)
г)

13
При полном пересечении (рисунок 3.1,а) линия пересечения рас-
падается на две линии АВС и ЕDК, причем эти линии могут быть как
плоскими, так и пространственными.
При неполном пересечении
(рисунок 3.1,в) линия пересечения
представляет собой замкнутую, как правило, пространственную
линию.
Возможно также полное пересечение с касанием ребер или гра-
ней (рисунок 3.1,б и 3.1,г). В первом случае линия пересечения имеет
одну общую точку С, во втором случае линия пересечения замыкается
на четыре точки пересекающихся ребер совпадающих граней (точки
А, С, Е, К).
Из приведенных рисунков видно, что линия пересечения в лю-
бом случае определяется точками пересечения ребер одного много-
гранника с гранями (или ребрами) другого или линиями пересечения
граней одного многогранника с гранями (или ребрами) другого.
В связи с этим линию пересечения можно построить также методом
ребер или методом граней, как и в случае построения сечения много-
гранников.
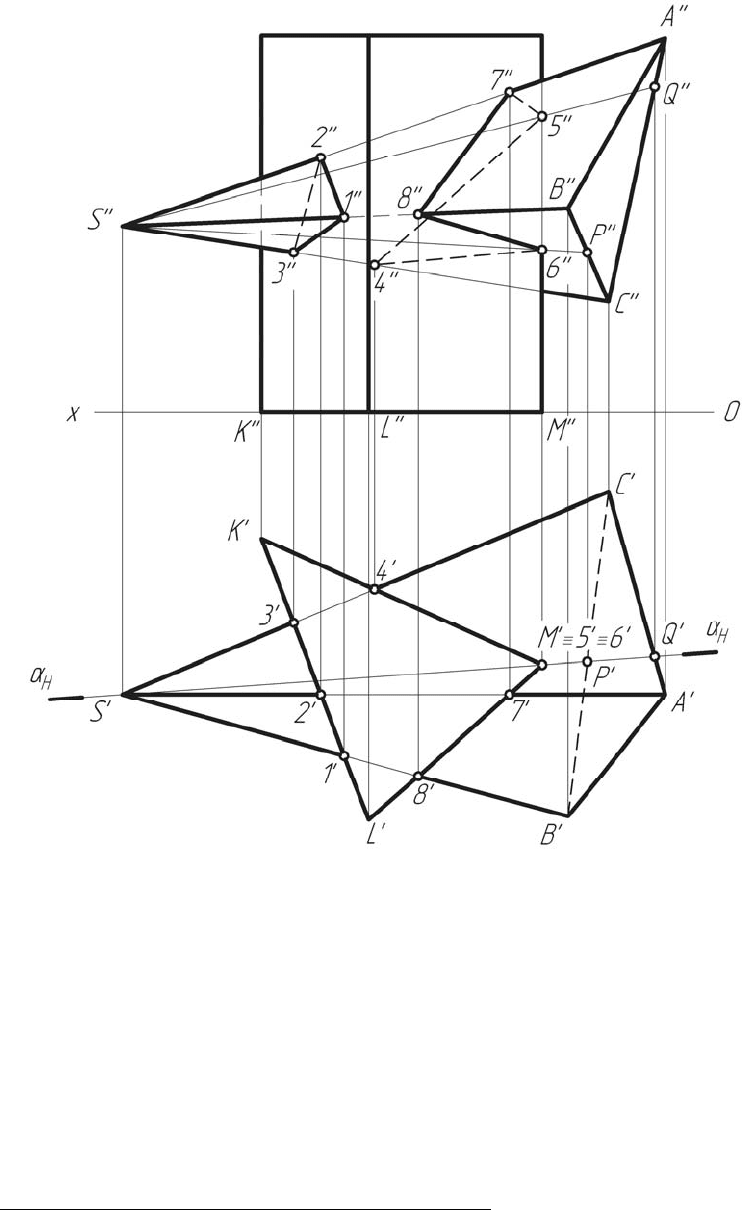
Рассмотрим задачу о пересечении многогранников, если один из
них находится в частном положении (рисунок 3.2). Пересекаются го-
ризонтально-проецирующая призма и пирамида.
Схема решения задачи:
- на горизонтальной проекции находим точки встречи ребер SC,
SA, SB пирамиды с гранями призмы (точки 1
/
, 2
/
, 3
/
, 4
/
, 7
/
, 8
/
). Далее
находим фронтальные проекции этих точек;
- ребро призмы М пересекается с гранями пирамиды SCA и SBC
в двух точках 5 и 6, которые совпадают с точкой М на горизонтальной
плоскости проекций (М
/
º
5
/
º
6
/
). Фронтальные проекции этих точек
находим с помощью горизонтально-проецирующей плоскости a, про-
веденной через вершину S пирамиды и ребро М призмы. Вспомога-
тельная плоскость пересекает пирамиду по двум линиям SQ и SP. На
фронтальных проекциях S
//
Q
//
и S
//
P
//
находим точки 5
//
и 6
//
;
- соединяем точки 1–2–3–1 и 8–7–5–4–6–8 и получаем две ли-
нии пересечения. Первая линия плоская, вторая – пространственная.
Обе линии – замкнутые. Пересечение многогранников полное.
14
Схема соединения точек: 1–2–3–1; 8–7–5–4–6–8
Рисунок 3.2 – Построение линии пересечения многогранников,
один из которых находится в частном положении
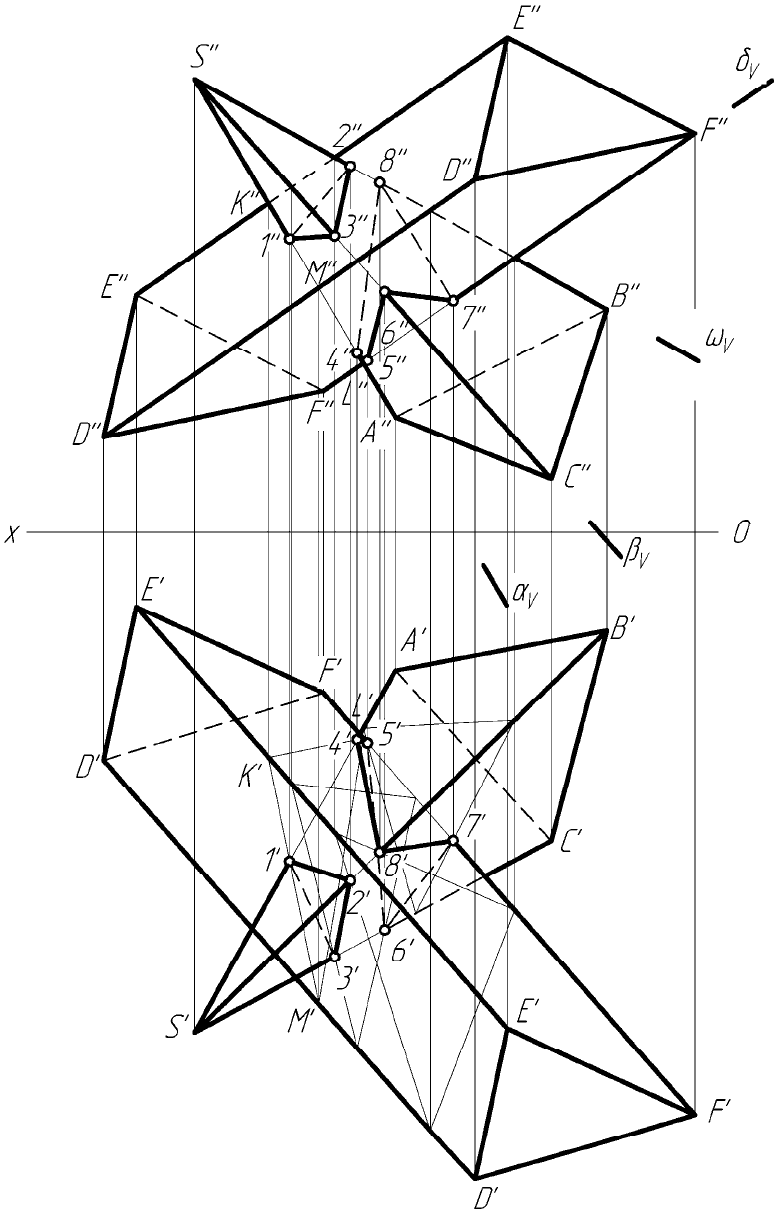
Решим задачу о пересечении двух многогранников общего по-
ложения (рисунок 3.3).
Задача решается следующим образом:
- сначала для облегчения дальнейших построений определим
видимость всех ребер многогранников (методом конкурирующих
точек);
- используем метод ребер. Назначаем задачи о пересечении ре-
бер многогранников с поверхностью другого многогранника;
15
Схема соединения точек: 1–2–3–1; 4–5–6–7–8–4
Рисунок 3.3 – Построение линии пересечения многогранников
общего положения методом ребер
16
- находим, например, точки пересечения ребра пирамиды SA с
поверхностью призмы. Для этого проводим через SA вспомогатель-
ную плоскость a;
- строим сечение призмы вспомогательной плоскостью a. В се-
чении получится треугольник KLM;
- находим общие точки ребра SA и контура треугольника и по-
лучим точки встречи ребра SA с поверхностью призмы – 1 и 4;
- далее аналогично находим точки встречи ребер SB, SC и FF.
Ребра ЕЕ и DD призмы с пирамидой не пересекаются;
- соединяем точки 1, 2 и 3, которые образуют один участок ли-
нии пересечения. Соединяем точки 4, 5, 6, 7 и 8, которые образуют
второй участок линии пересечения. Линия 4–5–6–7–8–4 – пространст-
венная;
- методом конкурирующих прямых определяем видимость всех
точек и участков линии пересечения;
- окончательно обводим чертеж с учетом видимости ребер и
участков линии пересечения.
На рисунке 3.4 представлена задача о построении проекций мно-
гогранника с поперечным сквозным призматическим пазом. Эта зада-
ча также относится к пересечению многогранников, так как паз мож-
но уподобить трехгранной призме, вставленной в паз. Решение задачи
ясно из рисунка. Проекции точек 1, 2, 3 построены с помощью вспо-
могательных плоскостей a и b. Точки 2 и 3 могут быть построены и
без использования вспомогательных секущих плоскостей, так как они
являются характерными точками и находятся на ребре многогранни-
ка. В этом случае построения проводятся в следующем порядке: сна-
чала находят профильные проекции 2
///
и 3
///
, затем по свойству эпюра
Монжа находят горизонтальные проекции 2
/
и 3
/
.
На профильной проекции многогранника выполнен простой вер-
тикальный профильный разрез, совмещенный с видом для того, чтобы
показать сквозное призматическое отверстие.
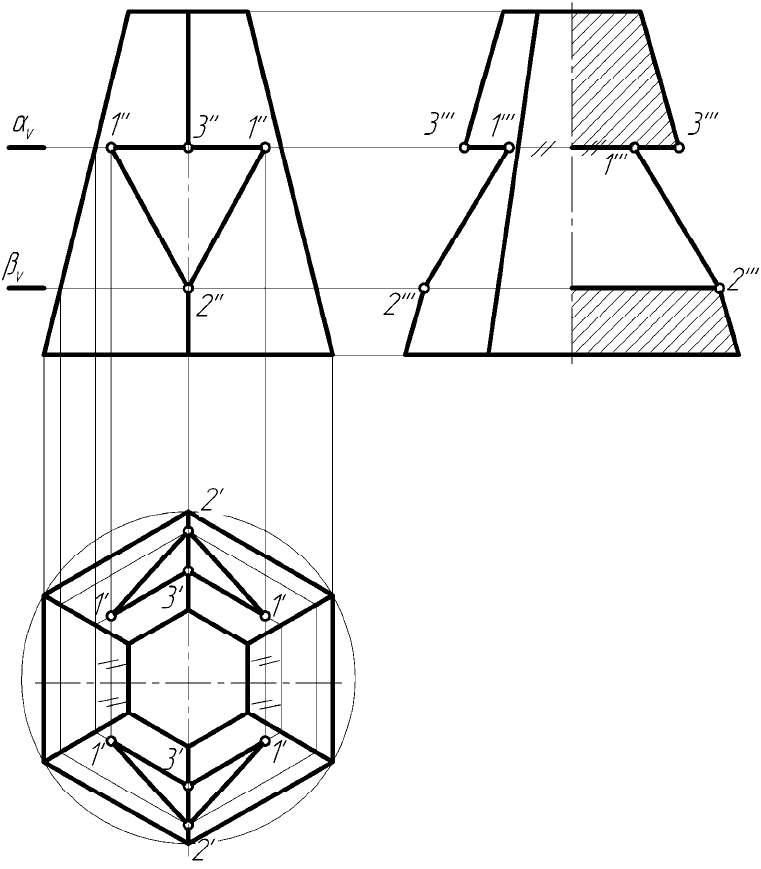
17
Рисунок 3.4 – Построение проекций многогранника
с поперечным сквозным трехгранным призматическим пазом
4 Общие сведения о кривых поверхностях
В самом общем виде поверхность может быть определена как
совокупность последовательных положений некой прямой или кривой
линии, называемой образующей, перемещающейся в пространстве по
некоторой другой прямой или кривой линии, называемой направ-
ляющей, по какому-либо закону.
В самом определении заложен главный способ образования
поверхностей – путем механического перемещения образующей.
Такой способ образования поверхности назван кинематическим
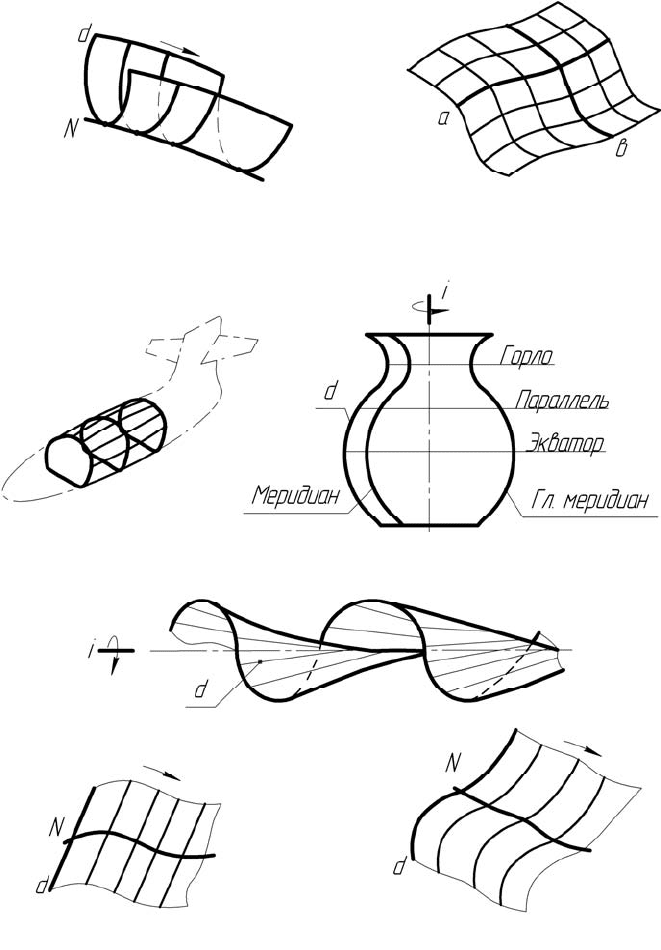
(рисунок 4.1,а). На рисунке 4.1: d – образующая, N – направляющая.
18
Рисунок 4.1 – Образование поверхностей
Несмотря на то, что кинематический способ образования по-
верхностей является всеобъемлющим, геометры отмечают и другие
способы образования, которые имеют свои отличительные признаки.
На рисунке 4.1,б, в представлен каркасный способ образования
поверхности. Каркасы подразделяются на точечные и линейные.
На рисунке 4.1,б для образования поверхности использован линейный
каркас, состоящий из двух ортогонально расположенных семейств
линий a и в. На рисунке 4.1,в показан каркас фюзеляжа самолета.
а)
б)
в)
г)
д)
е)
ж)
19
Поверхности вращения – это поверхности, которые образуются
какой-либо образующей при вращении ее вокруг неподвижной оси i
(рисунок 4.1,г).
Особую группу поверхностей образуют винтовые поверхности.
Винтовые поверхности могут быть образованы перемещением образую-
щей d (прямой или кривой линии) по винтовой линии (рисунок 4.1,д).
Если образующая d поверхности является прямой линией, то
поверхность называется линейчатой (рисунок 4.1,е), если образую-
щая d является кривой линией, то – нелинейчатой (рисунок 4.1,ж).
Классификация поверхностей является сложной математической
и геометрической задачей. Это обусловлено большим многообразием
поверхностей и, в первую очередь, тем, что та или иная поверхность
может быть образована различными способами, приводящими к од-
ному и тому же результату.
В связи с этим деление поверхностей по способу образования
может быть предельно условно. Однако при определенных допуще-
ниях классификация поверхностей по способу образования является
закономерной.
На рисунке 4.2 представлена классификация кривых поверхно-
стей. В данной классификации проведена систематизация поверхно-
стей по двум параметрам: по общим геометрическим свойствам и по
способам образования поверхностей. Указанные параметры являются
наиболее общими для всех поверхностей.
При разработке классификации сделано допущение, что поверх-
ности могут быть образованы только одним способом. Поверхности
вращения и винтовые поверхности не отнесены к кинематическим
поверхностям в связи с тем, что имеют свои и только им присущие
особенности перемещения образующей (вращение вокруг оси и пере-
мещение по винтовой линии).
Разделение поверхностей по общим свойствам и способам обра-
зования позволяет упростить классификацию поверхностей.
Поверхности могут быть заданы аналитически, табличным спо-
собом и графически. Если поверхность может быть описана уравне-
нием, то она называется закономерной, в противном случае – неза-
кономерной. Закономерные поверхности могут быть алгебраически-
ми и трансцендентными.
В зависимости от степени уравнения алгебраические поверхно-
сти могут быть второго и высшего порядков. Незакономерные поверх-
ности в основном являются графическими, среди которых можно выде-
