Кирин Е.М., Базыкина Н.А., Вантеев А.Н., Краснов М.Н. Построение сечений и линий пересечения поверхностей
Подождите немного. Документ загружается.



МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Государственное образовательное учреждение
высшего профессионального образования
«Пензенский государственный университет» (ПГУ)
Построение сечений и линий
пересечения поверхностей
Методические указания
Пенза
Издательство ПГУ
2011

2
УДК 744(07)
П63
Р е ц е н з е н т
ведущий инженер ОАО «Пензенский часовой завод»
П. М. Великанов
Составители:
Е. М. Кирин, Н. А. Базыкина,
А. Н. Вантеев М. Н. Краснов
Построение сечений и линий пересечения поверхностей :
П63 метод. указания. – Пенза : Изд-во ПГУ, 2011. – 64 с.
Рассмотрены наиболее сложные темы курса: построение сечений мно-
гогранников и кривых поверхностей, взаимное пересечение поверхностей.
Представлены основные методы построения сечений и линий пересечения
поверхностей.
Методические указания разработаны на кафедре «Начертательная
геометрия и графика» и предназначены для студентов, изучающих дисцип-
лину «Начертательная геометрия и инженерная графика».
УДК 744(07)
© ГОУ ВПО «Пензенский государственный
университет», 2011

3
СОДЕРЖАНИЕ
Введение .................................................................................................... 4
1 Общие сведения о многогранниках....................................................... 5
2 Построение сечений многогранников................................................... 7
3 Построение линии пересечения многогранников.................................12
4 Общие сведения о кривых поверхностях..............................................17
5 Построение сечений кривых поверхностей ..........................................21
5.1 Точка на поверхности ......................................................................21
5.2 Конические, цилиндрические, сферические и торовые сечения ...24
5.3 Построение сечений тел вращения .................................................25
6 Взаимное пересечение поверхностей....................................................31
6.1 Общие положения............................................................................31
6.2 Частные случаи пересечения поверхностей...................................33
6.3 Построение линии пересечения поверхностей методом
образующих и параллелей ..............................................................38
6.4 Метод вспомогательных секущих плоскостей...............................39
6.5 Метод вспомогательных концентрических сфер ...........................43
6.6 Метод вспомогательных эксцентрических сфер............................45
6.7 Построение линий пересечения поверхностей с помощью
вспомогательных плоскостей общего положения .........................47
7 Построение линий пересечения с использованием средств
компьютерной графики ........................................................................50
Список литературы...................................................................................57
Приложение ..............................................................................................58
4
Введение
Темы курса начертательной геометрии «Сечение поверхностей
плоскостями частного и общего положения» и «Взаимное пересече-
ние поверхностей» являются наиболее важными темами этой дисцип-
лины в теоретическом и практическом смысле. По сути дела весь курс
начертательной геометрии как бы подчинен обоснованию, разработке
и изложению способов построения сечений поверхностей и линий их
взаимного пересечения.
Особая важность перечисленных тем обусловливается их прак-
тической значимостью для конструирования машин, их деталей и
конструкций. Действительно, в каждой технической форме можно
найти сечения и линии пересечения отдельных элементов, которые
необходимо вычерчивать на чертежах и изготавливать в натурных об-
разцах. Практически во всех отраслях производства (машинострое-
ние, авиастроение, судостроение, приборостроение и др.) использу-
ются методы начертательной геометрии (графические методы) для
разработки чертежей конструкций, в которых необходимо решать
графические задачи по построению сечений различных деталей и ли-
ний пересечения технических форм.
В настоящих методических указаниях изложены краткие сведе-
ния о поверхностях и их классификации, представлены основные ме-
тоды построения сечений и линий пересечения поверхностей, даны
образцы учебных заданий по темам.
Все многообразие поверхностей в настоящих методических ука-
заниях разделено на две группы – гранные поверхности (многогран-
ники) и кривые поверхности, что позволяет улучшить структуру по-
собия и удобство пользования им. Основные термины и определения
в тексте выделены подчеркиваниями.
В отличие от большинства учебников по курсу «Начертательная
геометрия» в настоящих методических указаниях материал изложен в
сжатом и доступном для понимания виде и не перегружен теоретически-
ми материалами. Примеры построения сечений и линий пересечений по-
добраны так, чтобы студент освоил методику решения задач и использо-
вал ее для выполнения эпюров и чертежей по своему варианту. При объ-
яснении решения задач широко использован основной и эффективный
метод – поэтапное решение графических задач.
Методические указания предназначены для студентов всех спе-
циальностей, изучающих начертательную геометрию, для студентов-
дипломников и инженеров-конструкторов предприятий и конструк-
торских бюро.

5
1 Общие сведения о многогранниках
Многогранники относятся к поверхностям, точнее, к гранным
поверхностям, грани которых являются плоскостями. В связи с этим
многогранники целесообразно выделить в отдельный вид поверх-
ностей.
Многогранниками называются тела, ограниченные плоскими
n-угольниками, которые называются гранями. Линии пересечения
граней называются ребрами
. Точки пересечения ребер – вершинами.
Для всех многогранников справедлива формула Эйлера: сумма числа
граней и вершин за минусом числа ребер есть величина постоянная, и
равняется двум:
Г + В – Р = 2.
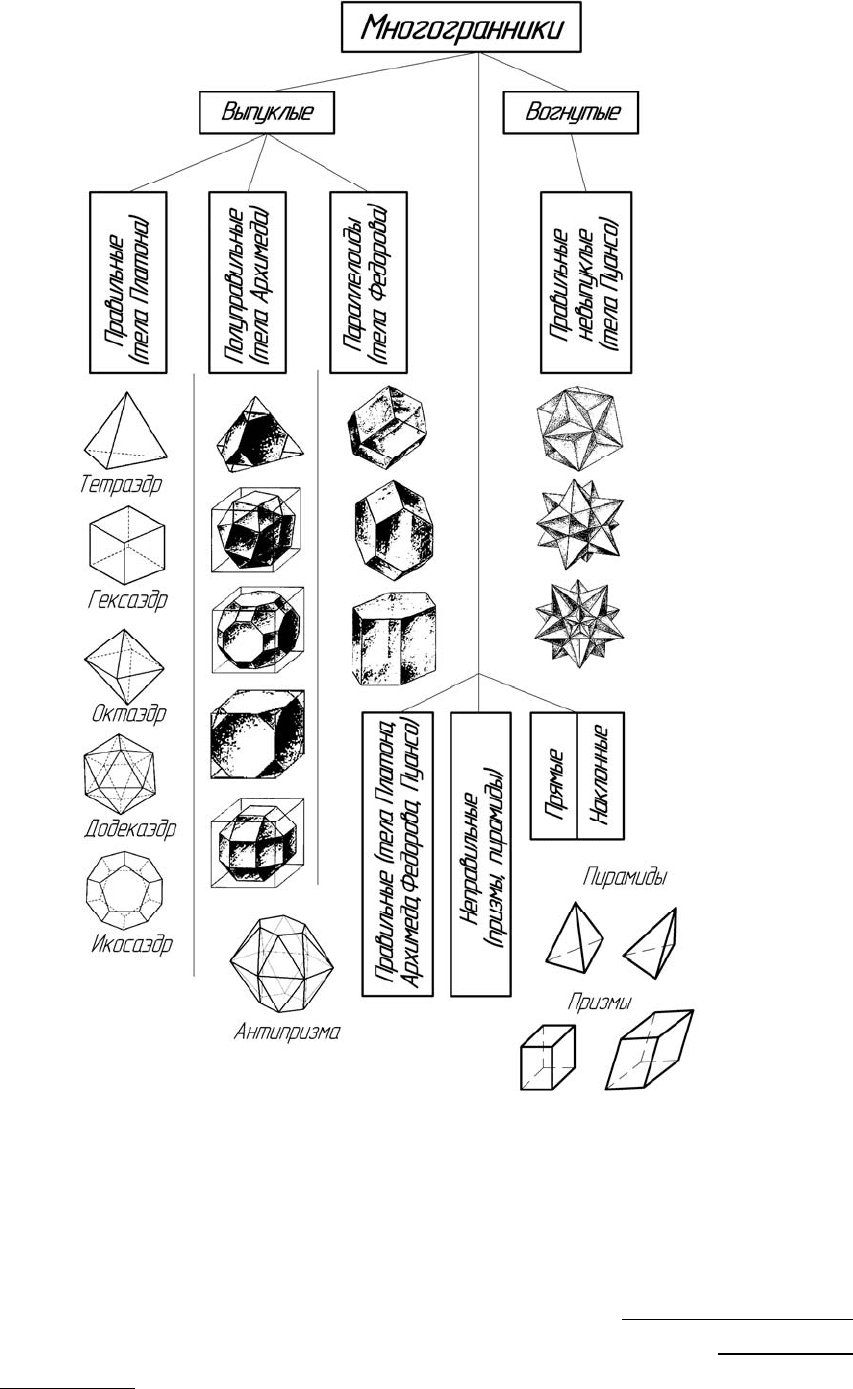
На рисунке 1.1 приведена классификация многогранников.
Большую группу многогранников составляют правильные и полупра-
вильные многогранники. Они характеризуются одинаково правиль-
ными гранями (грани – правильные треугольники, четырехугольники,
пятиугольники и т.д.); одинаковым числом ребер, сходящихся в каж-
дой вершине; одинаковыми многогранными углами при вершинах.
Полуправильные многогранники – это правильные многогранники со
срезанными вершинами.
Выпуклыми
многогранниками называются многогранники, рас-
полагаемые по одну сторону каждой грани. Если это условие не со-
блюдается, то многогранники называются вогнутыми или выпукло-
вогнутыми.
Приведем примеры правильных многогранников, называемых
телами Платона. Евклид доказал, что правильных многогранников
может быть не больше пяти. Это следует из подсчета суммы плоских
углов при вершинах любого многогранника.
Тетраэдр – это четырехгранник, все грани которого являются
равносторонними треугольниками.
Гексаэдр (куб) – это шестигранник, все грани которого являются
квадратами.
Октаэдр – это восьмигранник, все грани которого являются рав-
носторонними треугольниками.
Додекаэдр – двенадцатигранник, все грани которого являются
правильными треугольниками.
6
Рисунок 1.1 – Классификация многогранников
Икосаэдр – двадцатигранник, все грани которого – равносто-
ронние правильные треугольники.
Полуправильные многогранники называются телами Архимеда
(существует 13 типов тел Архимеда). Иногда их называют изоэдрами
или изогонами.

7
Русский ученый Е. С. Федоров в 1881 г. выделил выпуклые мно-
гогранники, рассматриваемые как тела, параллельным переносом ко-
торых можно заполнить все бесконечное пространство так, чтобы они
не входили друг в друга и не оставляли пустот между собой. Такие
многогранники называются параллелоэдрами или телами Федорова
(число их – 5, число граней – 6, 8, 10, 12, 14).
Правильные невыпуклые (выпукло-вогнутые) многогранники
называются телами Пуансо (четыре вида). В этих многогранниках ли-
бо грани пересекают друг друга, либо сами грани – самопересекаю-
щиеся многоугольники.
Наиболее распространенными в технике многогранниками яв-
ляются правильные и неправильные, прямые и наклонные призмы и
пирамиды, а также призматоиды.
Призма – это многогранник, в двух основаниях которого нахо-
дятся плоские n-угольники, а остальные грани являются параллело-
граммами.
Пирамида – это многогранник, в основании которого находится
плоский n-угольник, а остальные грани являются треугольниками с
общей вершиной.
Призматоид – это многогранник, ограниченный двумя парал-
лельными основаниями и боковой поверхностью, состоящей из тре-
угольников или трапеций.
На эпюре многогранники задаются проекциями ребер и вершин,
совокупность которых называют сеткой. Поверхность многогранни-
ков считается геометрически непрозрачной, в связи с чем на эпюре
следует определить видимость ребер методом конкурирующих точек
(прямых).
Многогранники как простейшие пространственные формы ис-
пользуются с древних времен (египетские пирамиды) по настоящее
время в строительстве, в инженерных конструкциях, архитектуре и т.д.
2 Построение сечений многогранников
Сечением называется плоская фигура, которая образуется при
пересечении поверхности многогранника или другой поверхности се-
кущей плоскостью. В зависимости от направления секущей плоскости
в сечении многогранников может быть треугольник, четырехуголь-
ник, пятиугольник и т.д. Если секущая плоскость параллельна плос-
8
кости проекций, то сечение проецируется на эту плоскость в нату-
ральную величину. В любом другом случае натуральную величину
сечения необходимо определять любым методом начертательной гео-
метрии (например, методом перемены плоскостей проекций).
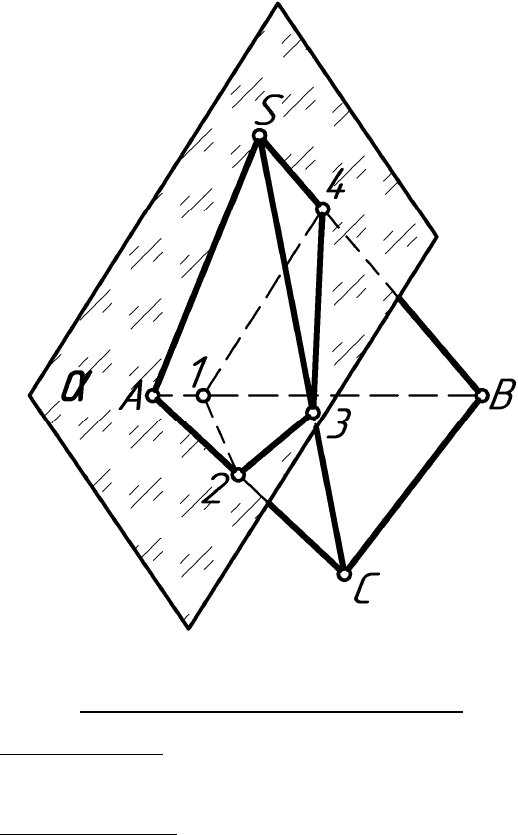
На рисунке 2.1 представлено два способа построения сечения
многогранников. Первый способ называют способом ребер, так как
он основывается на нахождении точек пересечения ребер с секущей
плоскостью, т.е. при построении сечения решают несколько раз типо-
вую задачу о пересечении прямой с плоскостью. Полученные точки
соединяют прямыми линиями.
a
Ç
SABC Þ Сечения 1–2–3–4
Метод ребер: АВ
Ç
a Þ 1; АС
Ç
a Þ 2;
SC
Ç
a Þ 3; SB
Ç
a Þ 4;
Метод граней
: АВС
Ç
a Þ 1–2; SAC
Ç
a Þ 2–3;
SBC
Ç
a Þ 3–4; SAB
Ç
a Þ 4–1.
Рисунок 2.1 – Два метода построения сечения многогранников
9
Второй способ построения сечения называют способом граней.
Согласно этому способу находят линии пересечения граней многогран-
ника с секущей плоскостью т.е. несколько раз решают типовую задачу о
пересечении плоскостей. Наиболее эффективным является способ ребер.
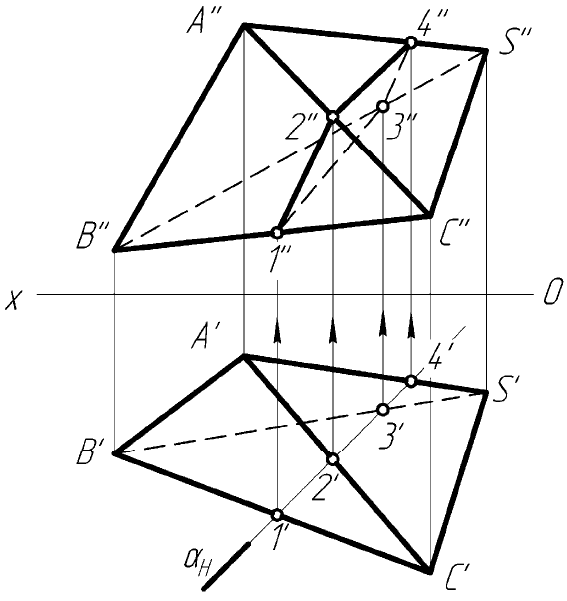
Рассмотрим построение сечения многогранника плоскостью ча-
стного положения (рисунок 2.2). В примере секущая плоскость явля-
ется горизонтально-проецирующей. Решаем задачу методом ребер.
На эпюре видно, что на горизонтальной проекции ребра BC, AC, SB
и AS пересекаются со следом a
Н
плоскости в точках 1
/
, 2
/
, 3
/
, 4
/
. По
линиям связи находим фронтальные проекции данных точек. На гори-
зонтальной проекции определяем последовательность соединения то-
чек: 1–2–4–3–1 (с учетом видимости ребер). Соединяем полученные
точки прямыми линиями.
Схема соединения точек: 1–2–4–3–1
Рисунок 2.2 – Построение сечения пирамиды
горизонтально-проецирующей плоскостью
Задача усложняется, если секущая плоскость является плоско-
стью общего положения. В этом случае точки пересечения ребер с се-
кущей плоскостью необходимо находить, используя методику реше-
ния задачи о пересечении прямой с плоскостью.
