King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

% Compute model

x = 1:.1:length(data);

y = p(3)/sqrt(2*pi*p(2)^2)* ...

exp(-(x - p(1)).^2/(2*p(2)^2)) + p (4);

% Compare data with the Gaussian model

ﬁgure(i)

plot(data(:,1),data(:,2),‘ko’,x,y,’k-’)

xlabel(‘{\itx}’, ‘FontSize’,24)

ylabel(‘Intensity’, ‘FontSize’,24)

set(gca, ‘LineWidth’,2, ‘FontSize’,20)

end

MATLAB program 8.15

function SSE = PixelSSE(p)

% Calculates the SSE between the observed pixel intensity and the

% Gaussian function

% f = a1/sqrt(2*pi)/sig*exp(-(x-mu)^2/(2*sig^2)) + a2

global data

% model parameters

mu = p(1); % mean

sig = p(2); % standard deviation

a1 = p(3); % rescales the distribution

a2 = p(4); % baseline

SSE = sum((data(:,2) - a1./sqrt(2*pi)./sig.* ...

exp(-(data(:,1) - mu). ^2/(2*sig.^2)) - a2).^2);

Note the use of string variables (and string concatenation) to generate filenames; together with the

load function this is used to automatically analyze an entire directory of up to 999 input files. Also,

this program provides an example of the use of the global declaration to pass a data file between a

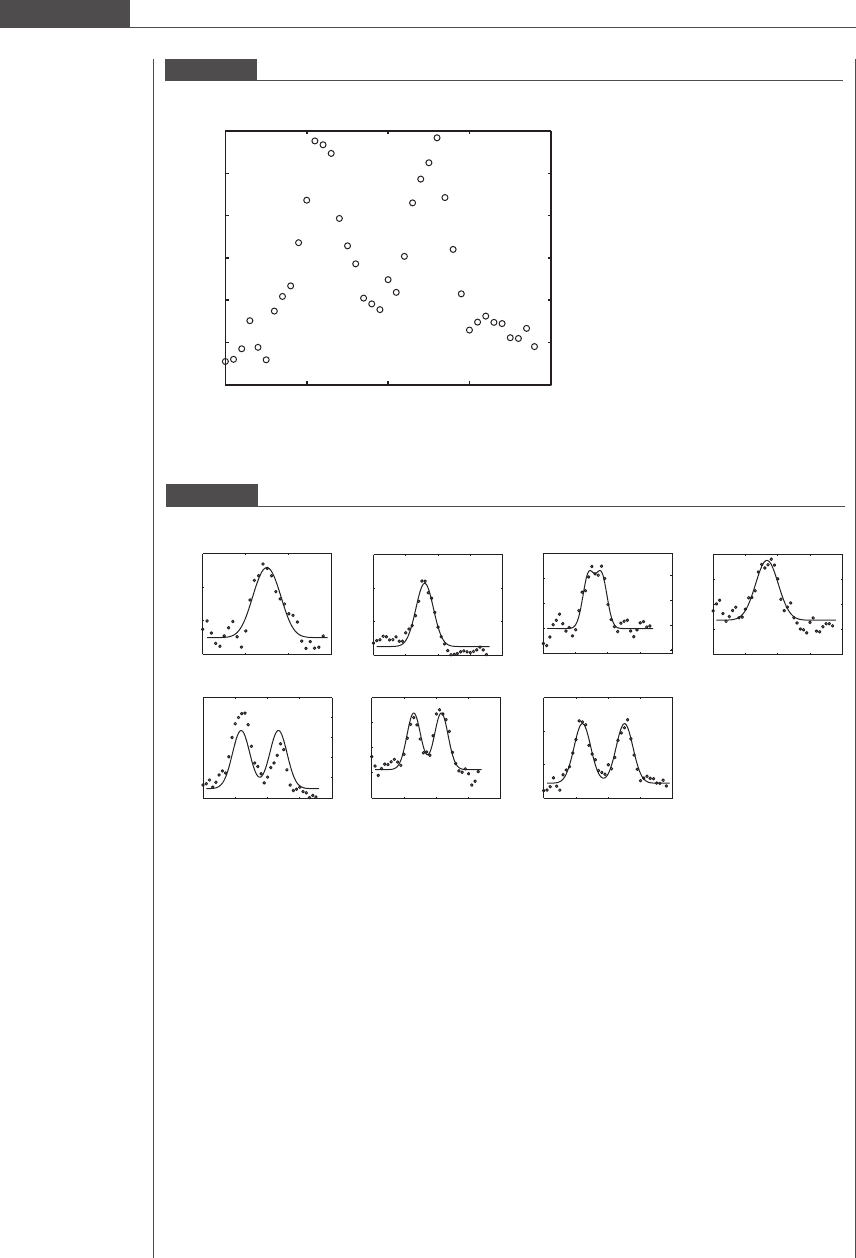
function and the main program. Figure 8.15 shows the good fits that were obtained using Program 8.14

to analyze four representative data files.

This program works well, and reliably finds a best-fit Gaussian model, but what happens when the

cell synapse begins to separate and show a distinct bimodal appearance such as shown in Figure 8.16?

It seems more appropriate to fit data such as this to a function comprising two Gaussian distributions,

rather than a single Gaussian. The following function is defined:

fðxÞ¼a



ﬃﬃﬃﬃﬃﬃﬃﬃ

2πσ

exp 

x  μ

ðÞ

2σ

ﬃﬃﬃﬃﬃﬃﬃﬃ

2πσ

exp 

x  μ

ðÞ

2σ

! !

þ a

Figure 8.15

Observed pixel intensities at four cell synapses and the fitted Gaussian models

0 10 20 30 40

100

120

140

160

Intensity

0 10 20 30 40

100

120

140

160

180

Intensity

0 10 20 30 40

100

150

200

250

Intensity

0 10 20 30

100

120

140

160

Intensity

517

8.3 Unconstrained multivariable optimization

Note that we have reduced the degrees of freedom by making the two Gaussian curves share the same

scaling factor a

and the same σ; the rationale for this restriction is discussed below. It is desirable that the

new bimodal analysis program be robust enough to converge on both unimodal and bimodal data sets, to

avoid the need to check each curve visually and make a (potentially subjective) human decision on each

data set ... as this would defeat the purpose of our file input commands capable of analyzing up to 999

files in one keystroke! The improved, bimodal algorithm is implemented in Programs 8.16 and 8.17 given

below. The relevant metric to characterize the width of the bimodal curve is now μ

 μ

added to some

multiple of σ. As shown in Figure 8.17, Program 8.16 reliably fits both unimodal and bimodal pixel

intensity curves.

The images in the first row of Figure 8.17 show the apparently unimodal images that were previously

analyzed using Program 8.15, and those in the second row show obviously bimodal images; Program

8.17 can efficiently characterize both types. Interestingly, initially the third image appeared unimodal,

but upon closer inspection we see a dip in the middle of the pixel range that the bimodal regression

algorithm correctly detects as nearly (but not exactly) overlapping Gaussians. It was determined that if

additional parameters are added to the model: (i) two, distinct values for σ, or (ii) individual scaling

factors for each peak, then the least-squares regression will attempt to create an artificially low, or wide,

peak, or a peak that is outside of the pixel range, in an attempt to deal with an uneven baseline at the two

edges of the data range.

Figure 8.16

Pixel intensities exhibited by separating cell synapse

0 10 20 30 40

100

120

140

160

180

200

220

Intensity

Figure 8.17

Observed pixel intensities at seven cell synapses and the fitted bimodal Gaussian models

100

150

200

250

Intensity

100

120

140

160

180

Intensity

0 10 20 30 40

100

120

140

160

Intensity

0 10 20 30 40

100

120

140

160

180

Intensity

0 10 20 30 40

100

150

200

250

Intensity

0 10 20 30

100

120

140

160

Intensity

140

160

180

200

220

240

Intensity

010203040

01020 3040

518

Nonlinear model regression and optimization

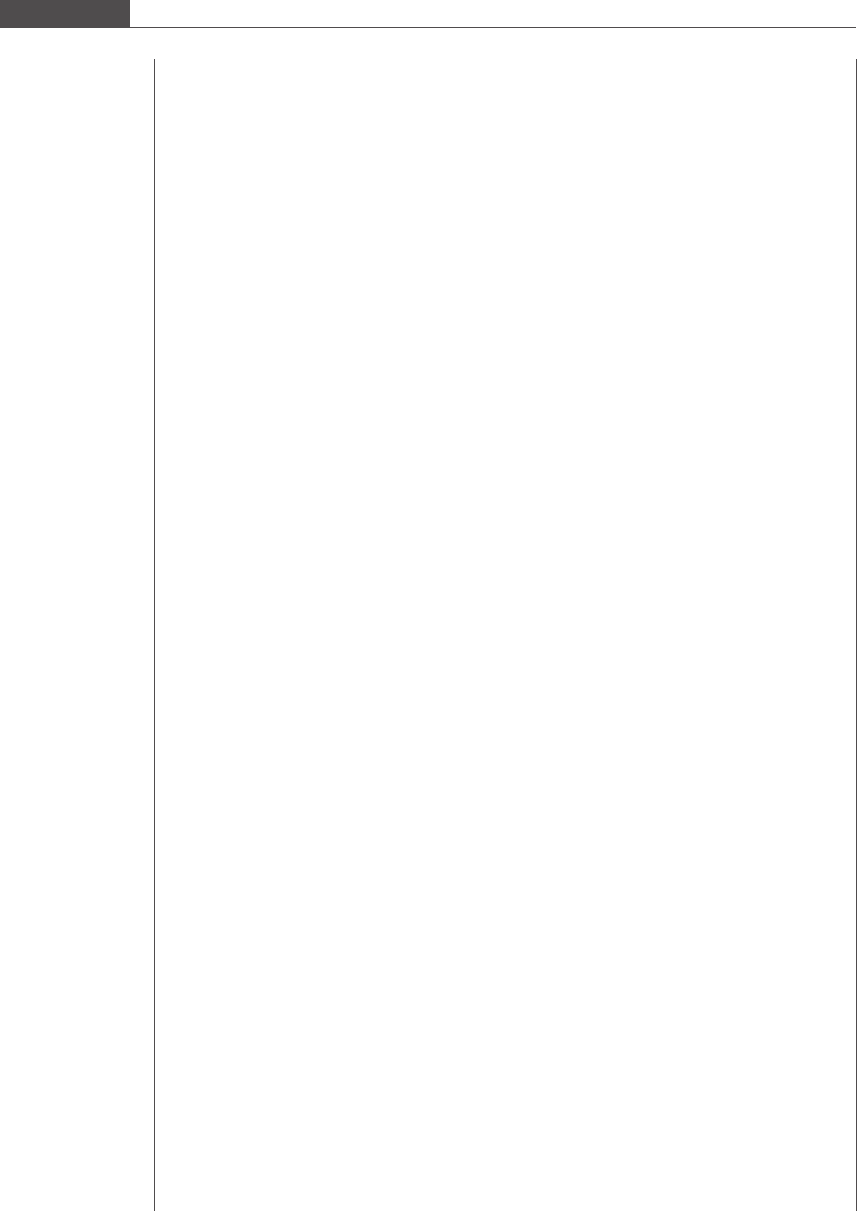
MATLAB program 8.16

% This program uses fminsearch to minimize the error of nonlinear

% least-squares regression of the bimodal Gaussian model to the pixel

% intensities data at a cell synapse

% To execute this program place the data ﬁles into the same directory in

% which this m-ﬁle is located.

% Variables

global data % matrix containing pixel intensity data

Nﬁles = 7; % number of data ﬁles to be analyzed, maximum allowed is 999

for i = 1:Nﬁles

num = num2str(i);

if length(num) == 1

ﬁlename=[‘data00’,num,’.dat’];

elseif length(num) == 2

ﬁlename = [ ‘ data0’,num,’.dat’];

else

ﬁlename = [ ‘ data’,num,’.dat’];

end

data = load(ﬁlename);

p = fminsearch(‘PixelSSE2’,[10,25,5,220,150]);

% Compute model

x = 1:.1:length(data);

y = p(4).* ...

(1/sqrt(2*pi*p(3).^2)*exp(-(x - p(1)).^2/(2*p(3).^2)) + ...

1/sqrt(2*pi*p(3).^2)*exp(-(x - p(2)).^2/(2*p(3).^2))) + p(5);

% Compare observations with the Gaussian model

ﬁgure(i)

plot(data(:,1),data(:,2),‘ko’,x,y,’k-’)

xlabel(‘[\itx]’, ‘FontSize’,24)

ylabel(‘Intensity’, ‘FontSize’,24)

set(gca, ‘LineWidth’,2, ‘FontSize’,20)

end

MATLAB program 8.17

function SSE = PixelSSE2(p)

% Calculates the SSE between the observed pixel intensity and the

% Gaussian function

% f = a1*(1/sqrt(2*pi*sig^2)*exp(-(x-mu1)^2/(2*sig^2))+ ...

% 1/sqrt(2*pi*sig^2)*exp(-(x-mu2)^2/(2*sig^2))) + a2

global data

% model parameters

mu1 = p(1); % mean of ﬁrst peak

mu2 = p(2); % mean of second peak

519

8.3 Unconstrained multivariable optimization

sig = p(3); % standard deviation

a1 = p(4); % rescales the distribution

a2 = p(5); % baseline

SSE = sum((data(:,2)-a1.* ...

(1/sqrt(2*pi*sig.^2)*exp(-(data(:,1)-mu1). ^2/(2*sig.^2))+ ...

1/sqrt(2*pi*sig.^2)*exp(-(data(:,1)-mu2).^2/(2*sig.^2)))-a2).^2);

Box 8.4A Kidney functioning in human leptin metabolism

The rate of leptin uptake by the kidney was modeled using Michaelis–Menten kinetics in Box 3.9A in

Chapter 3:

R ¼

max

þ S

In Box 3.9A, the rate equation was linearized to obtain the Lineweaver–Burk equation. Linear least-

squares regression was used to estimate the value of the two model parameters: R

max

and K

. Here, we

will use nonlinear regression to obtain estimates of the model parameters.

The best-fit parameters obtained from the linear regression analysis are used as the initial guessed

values for the nonlinear minimization problem:

¼ 10:87; R

max

¼ 1:732:

Our goal is to minimize the sum of the squared errors (residuals). Program 8.18 calculates the sum of

the squared residuals as

SSE ¼

i¼1



ðÞ

;

where

max

þ S

We use fminsearch (or the simplex algorithm) to locate the optimal values of R

max

and K

p = fminsearch(‘SSEleptinuptake’, [1.732, 10.87])

The fminsearch algorithm finds the best-fit values as R

max

¼ 4:194 and K

¼ 26:960. These

numbers are very different from the numbers obtained using the Lineweaver–Burk analysis.

We minimize again, this time using the fminunc function (line search method). Since we do not

provide a gradient function, the medium-scale optimization is chosen automatically by fminunc:

p2 = fminunc(’SSEleptinuptake’, [1.732, 10.87])

Warning: Gradient must be provided for trust-region method;

using line-search method instead.

Local minimum found.

Optimization completed because the size of the gradient is less than

the default value of the function tolerance.

p2 =

4.1938 26.9603

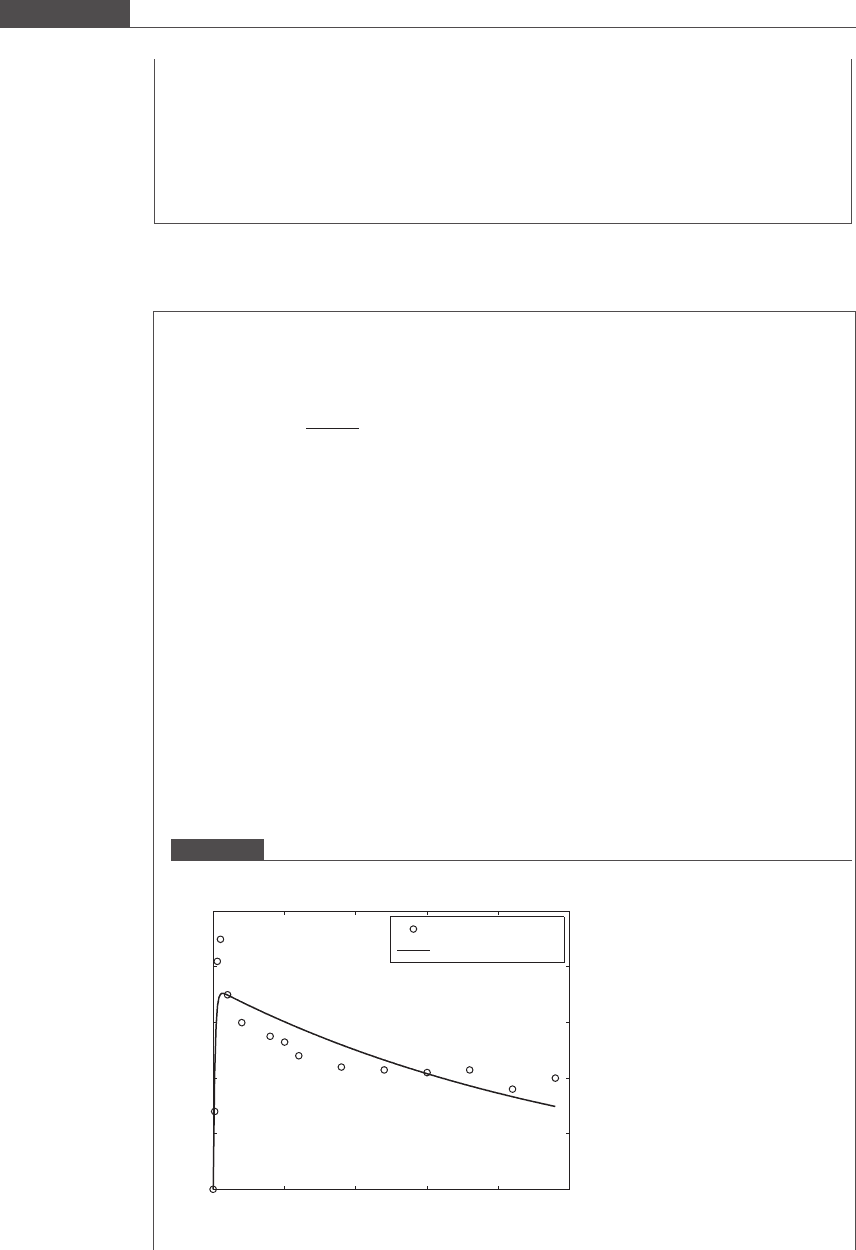
Both nonlinear search methods obtain the same minimum point of the SSE function. A plot of the data

superimposed with the kinetic model of leptin uptake fitted by (1) the line search method and (2) the

520

Nonlinear model regression and optimization

simplex method is shown in Figure 8.18. Included in this plot is the Michaelis–Menten model with

best-fit parameters obtained by linear least-squares regression. From Figure 8.18, you can see that the

fit of the model to the data when linear regression of the transformed equation is used is inferior to the

model fitted using nonlinear regression. Transformation of the nonlinear equation distorts the actual

scatter of the data points along the direction of the y-axis and produces a different set of best-fit model

parameters. In this example, the variability in the data is large, which makes it difficult to obtain

estimates of model parameters with good accuracy (small confidence intervals). For such experiments,

it is necessary to obtain many data points so that the process is well characterized.

MATLAB program 8.18

function SSE = SSEleptinuptake(p)

% Data

% Plasma leptin concentration

S = [0.75; 1.18; 1.47; 1.61; 1.64; 5.26; 5.88; 6.25; 8.33; 10.0; 11.11; ...

20.0; 21.74; 25.0; 27.77; 35.71];

% Renal Leptin Uptake

R = [0.11; 0.204; 0.22; 0.143; 0.35; 0.48; 0.37; 0.48; 0.83; 1.25; ...

0.56; 3.33; 2.5; 2.0; 1.81; 1.67];

% model variables

Rmax = p(1);

Km = p(2);

SSE = sum((R - Rmax*S./(Km + S)).^2);

MATLAB program 8.19

function SSE = SSEpharmacokineticsofAZTm(p)

global data

Figure 8.18

Observed rates of renal leptin uptake and the Michaelis–Menten kinetic model with different sets of best-fit

parameters

0 10 20 30 40

0.5

1.5

2.5

3.5

R (nmol/min)

S (n

/ml)

Observed data

Simplex method

Line search

Linear

transformation

521

8.3 Unconstrained multivariable optimization

Box 8.1B Pharmacokinetic and toxicity studies of AZT

The pharmacokinetic model for the maternal compartment is given by

tðÞ¼I

 k



k

 e

k



; (8:13)

where k

is the absorption rate constant for the maternal compartment, and the pharmacokinetic model

for the fetal compartment is given by

tðÞ¼I

1  e

k



; (8:14)

where k

is the absorption rate constant for the fetal compartment. Nonlinear regression is performed for

each compartment using fminsearch. Program 8.19 is a function m-file that computes the SSE for

the maternal compartment model. The data can be entered into another m-file that calls

fminsearch, or can be typed into the Command Window.

% Data

global data

time = [0; 1; 3; 5; 10; 20; 40; 50; 60; 90; 120; 150; 180; 210; 240];

AZTconc = [0; 1.4; 4.1; 4.5; 3.5; 3.0; 2.75; 2.65; 2.4; 2.2; 2.15; 2.1;

2.15; 1.8; 2.0];

data = [time, AZTconc];

Figure 8.19

Drug concentration profile in maternal compartment

0 50 100 150 200 250

t (min)

(mM)

Observed values

Nonlinear model

% model variables

Im = p(1);

km = p(2); % drug absorption rate constant

ke = p(3); % drug elimination rate constant

SSE = sum((data(:,2) - Im*km/(km - ke)*(exp(-ke.*data(:,1))- ...

exp(-km. *data(:,1)))).^2);

522

Nonlinear model regression and optimization

8.4 Constrained nonlinear optimization

Most optimization problems encountered in practice have constraints imposed on

the set of feasible solutions. As discussed in Section 8.1, a constraint placed on an

objective function fðxÞ can belong to one of two categories:

(1) equality constraints h

xðÞ¼0; j ¼ 1; 2; ...; m,and

(2) inequality constraints g

xðÞ0; k ¼ 1; 2; ...; p.

It is recommended that you create an m-file that loads the data into memory, calls the optimization

function, and plots the model along with the data. This m-file (pharmacokineticsofAZT.m)

is available on the book’s website.

The values of the parameters for the maternal compartment model are determined to be

¼ 4:612 mM,

¼ 0:833/min,

¼ 0:004/min.

The best-fit values for the fetal compartment model are

¼ 1:925 mM,

¼ 0:028/min.

The details of obtaining the best-fit parameters for the fetal compartment model are left as an exercise

for the reader.

Figures 8.19 and 8.20 demonstrate the fit between the models (Equations (8.13) and (8.14)) and the data.

What if we had used the first-order absorption and elimination model for the fetal compartment?

What values do you get for the model parameters?

Another way to analyze this problem is to couple the compartments such that

¼ k

;

where k

is the rate constant for transfer of drug from the maternal to the fetal compartment. In this case

you would have two simultaneous nonlinear models to fit to the data. How would you perform the

minimization of two sums of the squared errors?

Figure 8.20

Drug concentration profile in fetal compartment

0 50 100 150 200 250

0.5

1.5

2.5

t (min)

(mM)

Observed values

Nonlinear model

523

8.4 Constrained nonlinear optimization

The object ive function can be subjected to either one type of constraint or a mix of

both types of constraints. Optimization pro blems can have up to m equality con-

straints, where m < n and n is the number of variables to be optimized. An equality

or inequality constraint can be further classiﬁed as follows:

(1) a linear function in two or more variables (up to n variables),

(2) a nonlinear function in two or more variables (up to n variables),

(3) an assignment function (e.g. y ¼ 10) in the case of an equality constraint, or

(4) a bounding function (e.g. y  0; z  2) in the case of an inequality constraint.

In a one-dimensional optimization problem, only inequality constraints can be

imposed. An equality constraint placed on the objective function would immediately

solve the optimization problem. An inequality constraint(s), such as x  0andx  c,

where c is some constant, speciﬁes the search interval. Minimization (or maximization)

of the objective function is performed to locate the optimum x* within the interior of

the search interval. The function is then evaluated at the computed optimum x*, and

compared to the value of the function at the interval endpoints. If the function has the

least value at an endpoint (on the boundary of the variable space) then this point is

chosen as the feasible solution; otherwise the interior optimum, x*, is the answer.

For a multidimensional variable space, several methodo logies have been devised

to solve the constrained optimization problem . When only equality constraints have

been imposed, and m, the number of equality constraints, is small, the best way to

handle the optimization problem is to use the m constraints to reduce the number

of variab les in the objective function to (n – m). Example 8.3 illustrates how an

n-dimensional optimization problem with m equality constraints can be reduced to

an unconstrained optimization problem in (n – m) variables.

Example 8.3

Suppose we have a sheet of cardboard with surface area A. The entire cardboard surface is to be used to

construct a box. Maximize the volume of the open box with a square base that can be made out of this

cardboard.

Suppose each side of the base is of length x and the box height is h. The volume of the box is

V ¼ x

Our objective function to be maximized is

fx; h

ðÞ

¼ x

The surface area of the box is

A ¼ x

þ 4xh:

We have one nonlinear equality constraint,

hx; hðÞ¼x

þ 4xh  A ¼ 0:

We can eliminate the variable h from the objective function by using the equality constraint to obtain an

expression for h as a function of x. Substituting

h ¼

A  x

into the objective function, we obtain

fxðÞ¼x

A  x

524

Nonlinear model regression and optimization

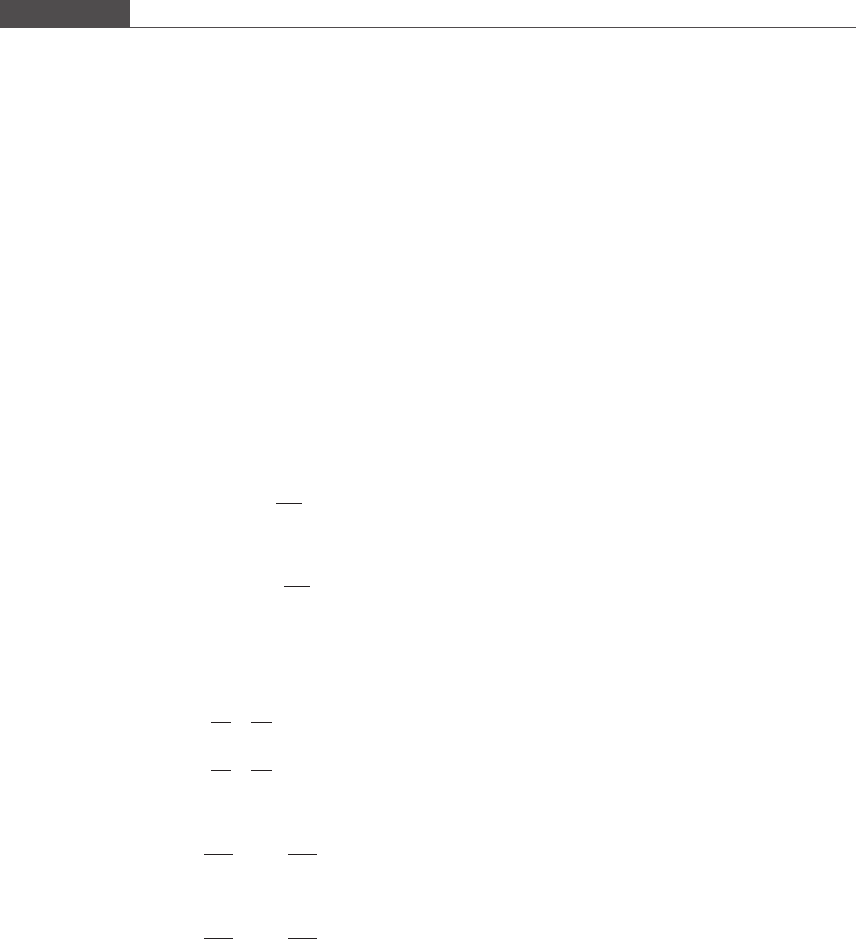
We have reduced the optimization problem in two variables subject to one equality constraint to an

unconstrained optimization problem in one variable. To find the value of x that maximizes V, we take the

derivative of fxðÞand equate this to zero. The resulting nonlinear equation is solved analytically to obtain

x ¼

ﬃﬃﬃﬃﬃﬃﬃﬃ

A=3

, and h ¼ 0:5

ﬃﬃﬃﬃﬃﬃﬃﬃ

A=3

. The maximum volume of the box

is calculated as A

3=2

ﬃﬃﬃ

In general, optimization problems with n > 2 variables subjected to m > 1 equality

constraints may not be reducible to an unconstrained optimization problem in (n – m)

variables. Unless the equality constraints are simple assignment functions or linear

equations, the complexity of the nonlinear equality constraints makes it difﬁcult to

express m variables in terms of the (n – m) variables.

A classical approach to solving a constrained problem is the Lagrange multiplier

method. In a constrained pro blem, the variables of the objective function are not

independent of each other, but are linked by the m equality constraints and some or

all of the p inequality constraints. Therefore, the partial derivatives of the objective

function with respect to each of the n variables cannot all be independently set to

zero. Consider an objective function fðxÞin n variables that is subjected to m equality

constraints h

ðxÞ. The following simultaneous conditions must be met at the con-

strained opt imum point:

df ¼

i¼1

∂f

∂x

¼ 0

and

i¼1

∂h

∂x

¼ 0:

Let’s consider the simplest case where n = 2 and m = 1. The trivial solution of the

two simultaneous linear equations is dx

¼ dx

¼ 0, which is not meaningful. To

ensure that a non-trivial solution exists, the determinant of the 2 × 2 coefﬁcient matrix

∂f

∂x

∂f

∂x

∂h

∂x

∂h

∂x



must equal zero. This is possible only if

∂f

∂x

¼l

∂h

∂x

and

∂f

∂x

¼l

∂h

∂x

;

where λ is called the Lagrange multiplier. To convert the constrained minimization

problem into an unconstrained problem such that we can use the techniques dis-

cussed in Section 8.3 to optimize the variables, we construct an augmented objective

function called the Lagrangian function:

; x

; lðÞ¼fx

; x

ðÞþlhx

; x

ðÞ:

If we take the partial derivatives of Lx

; x

; lðÞwith respect to the two variables and

the Lagrange multiplier, we obtain three simultaneous equations in three variables

whose solution yields the optimum, as follows:

Note that the solution of this problem is theoretical and not necessarily the most practical since a box of

these dimensions may not in general be cut from a single sheet of cardboard without waste pieces.

525

8.4 Constrained nonlinear optimization

∂L

∂x

∂f

∂x

þ l

∂h

∂x

¼ 0;

∂L

∂x

∂f

∂x

þ l

∂h

∂x

¼ 0;

∂L

∂l

¼ hx

; x

ðÞ¼0:

For an objective function in n variables subjected to m equ ality constraints, the

Lagrangian function is given by

L x; lðÞ¼f xðÞþ

j¼1

ðxÞ; (8:15)

where l ¼ l

; l

; ...; l

½. The constrained optimization problem in n variables has

been converted to an unconstrained problem in n + m variables. For x* to be a critical

point of the constrained problem, it must satisfy the following n + m conditions:

∂Lðx; lÞ

∂x

∂fðx; lÞ

∂x

j¼1

∂h

ðxÞ

∂x

¼ 0; i ¼ 1; 2; ...; n;

and

∂Lðx; lÞ

∂l

¼ h

xðÞ¼0; j ¼ 1; 2; ...; m:

To ﬁnd the optimum, one can solve either Equation (8.15) using unconstrained

optimization techniques discussed in Section 8.3 or the set of n + m equations

given by the necessary conditions. In other words, while the optimized parameters

of an uncon strained problem are obtained by solvi ng the set of equations given

rf ¼ 0 ;

for a constrained problem we must solve the augmented set of equations given by



L ¼ 0 ;

where





How does one incorporate p inequality constraints into the optimization analysis?

This is done by converting the inequality constraints into equality constraints using

slack variab les:

xðÞþσ

¼ 0; k ¼ 1; 2; ...; p;

where σ

are called slack variables. The term is squared so that the slack variable

term will always be either equal to or greater than zero. If a slack variable σ

is zero at

any point x, then the kth inequality constraint is said to be active and x lies on the

boundary speciﬁed by the constraint g

xðÞ.Ifσ

6¼ 0, then the point x lies in the

interior of the boundary and g

xðÞis said to be an inactive inequality constraint. If p

inequality constraints are imposed on the objective function, one must add p

Lagrange multipliers to the set of variables to be optimized and p slack variables.

526

Nonlinear model regression and optimization