King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

industrial design, trafﬁc control, meteorology, and econ omics. In this chapter,

several well-established classical optimization tools are presented; however, our

discussion only scratches the surface of the body of optimization literature currently

available. We ﬁrst address the topic of unconstrained optimization of one variable in

Section 8.2. We demonstrate three classic methods used in one-dimensional mini-

mization: (1) Newton’s method (see Section 5.5 for a demonstration of its use as a

nonlinear root-ﬁnding method), (2) successive parabolic interpolation method, and

(3) the golden section search method. The minimization problem becomes more

challenging when we need to optimize over more than one variable. Simply using a

trial-and-error method for multivariable optimization problems is discouraged due

to its inefﬁciency. Section 8.3 discusses popular methods used to perform uncon-

strained optimization in several dimensions. We discuss the topic of constrained

optimization in Section 8.4. Finally, in Section 8.5 we demonstrate Monte Carlo

techniques that are used in practice to estimate the standard error in the estimat es of

the model parameters.

8.2 Unconstrained single-variable optimization

The behavior of a nonlinear function in one variable and the location of its extreme

points can be studied by plotting the function. Consider any smooth function f in a

single variable x that is twice differentiable on the interval ½a; b.Iff

xðÞ

0 over any

interval x 2½a; b, then the single-variable function is increasing on that interval.

Similarly, when f

xðÞ

0 over any interval of x, then the single-variable function is

decreasing on that interval. On the other hand, if there lies a point x* in the interval

½a; b such that f



ðÞ¼0, the function is neither increasing nor decreasing at that

point.

In calculus courses you have learned that an extreme point of a continuous and

smooth function fðxÞ can be found by taking the derivative of fðxÞ, equating it to

zero, and solving for x. One or more solutions of x that satisfy f

xðÞ¼0 may exist.

The points x* at which f

ðxÞ equals zero are called critical points or stationary points.

At a critical point x*, the function is parallel with the x-axis. Three possibilities arise

regarding the nature of the critical point x*:

(1) if f



ðÞ¼0; f



ðÞ

0, the point is a local minimum;

(2) if f



ðÞ¼0; f



ðÞ

0, the point is a local maximum;

(3) if f



ðÞ¼0; f



ðÞ¼0, the point may be either an inﬂection point or an extreme

point. As such, this test is inconclusive. The values of highe r derivatives

000

xðÞ; ...; f

k1

xðÞ; f

xðÞare needed to deﬁne this point. If f

xðÞis the ﬁrst non-

zero kth derivative, then if k is even, the point is an extremum (minimum if f

xðÞ

maximum if f

xðÞ

0), and if k is odd, the critical point is an inﬂection point.

The method of establishing the nature of an extreme point by calculating the value

of the second derivative is called the second derivative test. Figure 8.3 graphic ally

illustrates the different types of critical points that can be exhibited by a nonlinear

function.

To ﬁnd the local minima of a function, one can solve for the zeros of f

ðxÞ, which

are the critical points of fðxÞ. Using the second derivative test (or by plotting the

function), one can then establish the character of the critical point. If f

xðÞ¼0isa

nonlinear equation whose solution is difﬁcult to obtain analytically, root-ﬁnding

methods such as those described in Chapter 5 can be used to solve iteratively for the

487

8.2 Unconstrained single-variable optimization

roots of the equation f

xðÞ¼0. We show how Newton’s root-ﬁnding method is used

to ﬁnd the local minimum of a single-variable function in Section 8.2.1.In

Section 8.2.2 we present another calculus-based method to ﬁnd the local minimum

called the polynomial approximation method. In this method the function is

approximated by a quadratic or a cubic function. The derivative of the polynomial

is equated to zero to obt ain the value of the next guess. Section 8.2.3 discusses a non-

calculus-based method that uses a bracketing technique to search for the minimum.

All of these methods assume that the function is unimodal.

8.2.1 Newton’s method

Newton’s method of one-dimensional minimization is similar to Newton’s nonlinear

root-ﬁnding method discussed in Section 5.5. The unimodal function fðxÞis approxi-

mated by a quadratic equation, which is obtained by truncating the Taylor series

after the third term. Expanding the function about a point x

fxðÞfx

ðÞþf

ðÞx  x

ðÞþ

ðÞx  x

ðÞ

At the extreme point x*, the ﬁrst derivative of the function must equal zero. Taking

the derivative of the expression above with respect to x, the expression reduces to

x ¼ x



ðÞ

: (8:1)

If you compare Equation (8.1) to Equation (5.19), you will notice that the

structure of the equation (and hence the iterative algorithm) is exactly the same,

except that, for the minimization problem, both the ﬁrst and second derivative need

to be calculated at each iteration. An advantage of this method over other one-

dimensional optimization methods is its fast second-order convergence, when con-

vergence is guaranteed. However, the initial guessed values must lie close to the

minimum to avoid divergence of the solution (see Section 5.5 for a discussion on

convergence issues of Newton’s method). To ensure that the iterative technique is

converging, it is recommended to check at each step that the cond ition fx

iþ1

ðÞ

fðx

is satisﬁed. If not, modify the initial guess and check again if the solut ion is

progressing in the desired direction.

Some difﬁcul ties encountered when using this method are as follows.

Figure 8.3

Different types of critical points

Local maxima

Local minima

Inflection

points

f (x)

488

Nonlinear model regression and optimization

(1) This method is unusable if the function is not smooth and continuous, i.e. the

function is not differentiable at or near the minimum.

(2) A derivative may be too complicated or not in a form suitable for evaluation.

(3) If f

xðÞat the critical point is equal to zero, this method will not exhibit second-order

convergence (see Section 5.5 for an explanation).

Box 8.2A Optimization of a fermentation process: maximization of profit

A first-order irreversible reaction A → B with rate constant k takes place in a well-stirred fermentor tank

of volume V. The process is at steady state, such that none of the reaction variables vary with time. W

the amount of product B in kg produced per year, and p is the price of B per kg. The total annual sales is

given by $ pW

The mass flowrate of broth through the processing system per year is denoted by W

.IfQ is the

flowrate (m

/hr) of broth through the system, ρ is the broth density, and the number of hours of operation

annually is 8000, then W

¼ 8000ρQ. The annualized capital (investment) cost of the reactor and the

downstream recovery equipment is $4000W

0:6

The operating cost c is $15.00 per kg of B produced. If the concentration of B in the exiting broth is

out

in molar units, then we have W

¼ 8000Qb

out

A steady state material balance incorporating first-order reaction kinetics gives us

out

¼ a

1 

1 þ kV=Q



;

where V is the volume of the fermentor and a

is the inlet concentration of the reactant. Note that as Q

increases, the conversion will decrease.

The profit function is given by

ðp  cÞW

 4000 W

ðÞ

0:6

;

and in terms of the unknown variable Q, it is as follows:

ðÞ

¼ 8000 p  c

ðÞ

1 

1 þðkV=QÞ



 4000 8000ρQ

ðÞ

0:6

: (8:2)

Initially, as Q increases the product output will increase and profits will increase. With subsequent

increases in Q, the reduced conversion will adversely impact the product generation rate while

annualized capital costs continue to increase.

You are given the following values:

p = $400 per kg of product,

ρ = 2.5 kg/m

=10μM(1M≡ 1 kmol/m

k = 2/hr,

V =12m

= 70 000 kg/kmol.

Determine the value of Q that maximizes the profit function. This problem was inspired by a

discussion on reactor optimization in Chapter 6 of Nauman (2002).

We plot the profit as a function of the hourly flowrate Q in Figure 8.4. We can visually identify an

interval Q 2½50; 70 that contains the maximum value of the objective function.

The derivative of the objective function is as follows:

QðÞ¼8000 p  cðÞMW

1 

1 þðkV=QÞ



QkV

Q þ kVðÞ

 0:6 

4000 8000ρðÞ

0:6

0:4

489

8.2 Unconstrained single-variable optimization

The second derivative of the objective function is as follows:

QðÞ¼8000 p cðÞMW



2 kVðÞ

Q þkVðÞ

þ 0:24 

4000 8000ρðÞ

0:6

1:4

Two functions are written to carry out the maximization of the profit function. The first function listed

in Program 8.1 performs a one-dimensional Newton optimization, and is similar to Program 5.7.

Program 8.2 calculates the first and second derivative of the profit function.

MATLAB program 8.1

function newtons1Doptimization(func, x0, tolx)

% Newton’s method is used to minimize an objective function of a single

% variable

% Input variables

% func : ﬁrst and second derivative of nonlinear function

% x0 : initial guessed value

% tolx : tolerance in estimating the minimum

% Other variables

maxloops = 20;

[df, ddf] = feval(func,x0);

fprintf(‘ i x(i) f’’(x(i)) f’’’’(x(i)) \n’); %\n is carriage return

% Minimization scheme

for i = 1:maxloops

x1 = x0 - df/ddf;

[df, ddf] = feval(func,x1);

fprintf(‘%2d %7.6f %7.6f %7.6f \n’,i,x1,df,ddf);

if (abs(x1 - x0) <= tolx)

break

Figure 8.4

Profit function

0 20 40 60 80 100

0.8

1.2

1.4

1.6

1.8

× 10

Q (m

/hr)

Annual profit (US dollars)

490

Nonlinear model regression and optimization

The termination criterion in Box 8.2A consisted of specifying a tolerance value for

the absolute difference in the solution of two consecutive iterations. Other stopping

criteria may be speciﬁed either individually or simultaneously.

(1) f

xðÞ

E . A cut-off value close to zero can be speciﬁed. If this criterion is met, it

indicates that f

ðxÞ is close enough to zero such that an extreme point has been

reached. This criterion can be used only with a minimization algorithm that calcu-

lates the derivative of the function.

(2)

iþ1

ðÞfx

ðÞ

iþ1

ðÞ



E. If the function value is changing very slowly, this can signify that a

critical point has been found.

(3)

iþ1

x

iþ1



E. The relative change in the solution can be used to determine when the

iterations can be stopped.

end

x0 = x1;

end

MATLAB program 8.2

function [df ddf] = ﬂowrateoptimization(Q)

% Calculates the ﬁrst and second derivatives of the proﬁt function

ain = 10e-6; % feed concentration of A (kmol/m^3)

p = 400; % price in US dollars per kg of product

c = 15; % operating cost per kg of product

k = 2; % forward rate constant (1/hr)

V = 12; % fermentor volume (m^3)

rho = 2.5; % density (kg/m^3)

MWB = 70000; % molecular weight (kg/kmol)

df = 8000*(p - c)*ain*MWB*(1 - 1/(1 + k*V/Q) - Q*k*V/(Q + k*V)^2) - ...

0.6*4000*(8000*rho)^0.6/(Q^0.4);

ddf = 8000*(p - c)*ain*MWB*(-2*(k*V)^2/(Q + k*V)^3) + ...

0.24*4000* (8000*rho)^0.6/(Q^1.4);

The optimization function is executed from the command line as follows:

newtons1Doptimization(‘ﬂowrateoptimization’, 50, 0.01)

i x(i) f’(x(i)) f’’(x(i))

1 57.757884 5407.076741 −3295.569935

2 59.398595 178.749716 −3080.622008

3 59.456619 0.211420 −3073.338162

4 59.456687 0.000000 −3073.329539

The optimum flowrate that maximizes the profit is Q = 59.46 m

/hr. The second derivative is negative,

which tells us that the critical point is a maximum. To use Newton’s optimization method we did not

need to convert the maximization problem to a minimization problem because the method searches for

an extreme point and does not formally distinguish between a minimum point and a maximum point.

In this problem, we did not specify any constraints on the value of Q. In reality, the flowrate will have

some upper limit that is dictated by the size of installed piping, frictional losses in the piping, pump

capacity, and other constraints.

491

8.2 Unconstrained single-variable optimization

8.2.2 Successive parabolic interpolation

In the successive parabolic interpolation method, a unimodal function is approxi-

mated over an interval x

; x

½that brackets the minimum by a parabolic function

pxðÞ¼c

þ c

x þ c

. Any three values of the independent variable, x

< x

not necessarily equally spaced in the interval, are selected to construct the unique

parabola that passes through these three points. The minimum point of the parabola

is located at p

xðÞ¼0. Taking the derivative of the second-degree polynomial

expression and equating it to zero, we obtain

min

¼

: (8:3)

The minimum given by Equation (8.3) will most likely not coincide with the mini-

mum x* of the objective function (unless the function is also parabolic); x

min

will lie

either between x

and x

or between x

and x

.Wecalculatefx

min

ðÞand compare this

with the function values at the three other points. The point x

min

andtwooutofthethree

original points are chosen to form a new set of three points used to construct the next

parabola. The selection is made such that the minimum value of fðxÞ is bracketed by the

endpoints of the new interval. For example, if x

min

> x

min

lies between x

and x

)

and fx

min

ðÞ

ðÞ, then we would choose the three points x

, x

min

,andx

. On the other

hand, if fx

min

ðÞ

ðÞand x

min

> x

, then we would choose the points x

, x

,andx

min

The new set of three points provides the next parabolic approximation of the function

near or at the minimum. In this manner, each newly constructed parabola is deﬁned

over an interval that always contains the minimum value of the function. The interval on

which the parabolic interpolation is deﬁnedshrinksinsizewitheachiteration.

To calculate x

min

, we must express c

and c

in Equation (8.3) in terms of the three

points x

, x

, and x

and their function values. We use the second-order Lagrange

interpolation formula given by Equation (6.14) (reproduced below) to construct a

second-degree polynomial approximation to the function:

pxðÞ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

ðÞþ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

ðÞ:

Differentiating the above expression and equating it to zero, we obtain

x  x

ðÞþx  x

ðÞ

 x

ðÞx

 x

ðÞ

ðÞþ

x  x

ðÞþx  x

ðÞ

 x

ðÞx

 x

ðÞ

x  x

ðÞþx  x

ðÞ

 x

ðÞx

 x

ðÞ

ðÞ¼0

Applying a common denominator to each term, the equation reduces to

2x  x

 x

ðÞx

 x

ðÞfx

ðÞ2x  x

 x

ðÞx

 x

ðÞfx

ðÞ

þ 2x  x

 x

ðÞx

 x

ðÞfx

ðÞ¼0

Rearranging, we get

min

 x



ðÞx

 x



ðÞþx

 x



ðÞ

 x

ðÞfx

ðÞx

 x

ðÞfx

ðÞþx

 x

ðÞfx

ðÞ

: (8:4)

We now summarize the algorithm.

492

Nonlinear model regression and optimization

Algorithm for successive parabolic approximation

(1) Establish an inter val within which a minimum point of the unimodal function lies.

(2) Select the two endpoints x

and x

of the interval and one other point x

in the

interior to form a set of three points used to construct a parabolic approximation of

the function.

(3) Evaluate the function at these three points.

(4) Calculate the minimum value of the parabola x

min

using Equation (8.4).

(5) Select three out of the four points such that the new interval brackets the minimum

of the unimodal function.

(a) If x

min

then

(i) if fx

min

ðÞ

ðÞchoose x

, x

min

, x

;

(ii) if fx

min

ðÞ

choose x

min

, x

(b) If x

min

then

(i) if fx

min

ðÞ

ðÞchoose x

, x

min

, x

;

(ii) if fx

min

ðÞ

ðÞchoose x

, x

min

(6) Repeat steps (4) and (5) until the interval size is less than the tolerance speciﬁcation.

Note that only function evaluations (but not derivative evaluations) are required,

making the parabolic interpolation useful for functions that are difﬁcult to differ-

entiate. A cubic approximation of the function may or may not require evaluation of

the function derivative at each iteration depending on the chosen algorithm. A

discussion of the non-derivative-based cubic approximation method can be found

in Rao (2002). The convergence rate of the successive pa rabolic interpolation

method is superlinear and is intermediate to that of Newton’s method discussed in

the previous section and of the golden section search method to be discussed in

Section 8.2.3.

Box 8.2B Optimization of a fermentation process: maximization of profit

We solve the optimization problem discussed in Box 8.2A using the method of successive parabolic

interpolation. MATLAB program 8.3 is a function m-file that minimizes a unimodal single-variable

function using the method of parabolic interpolation. MATLAB program 8.4 calculates the negative of

the profit function (Equation (8.2)).

MATLAB program 8.3

function parabolicinterpolation(func, ab, tolx)

% The successive parabolic interpolation method is used to ﬁnd the

% minimum of a unimodal function.

% Input variables

% func: nonlinear function to be minimized

% ab : bracketing interval [a, b]

% tolx: tolerance in estimating the minimum

% Other variables

k = 0; % counter

% Set of three points to construct the parabola

x0 = ab(1);

493

8.2 Unconstrained single-variable optimization

x2 = ab(2);

x1 = (x0 + x2)/2;

% Function values at the three points

fx0 = feval(func, x0);

fx1 = feval(func, x1);

fx2 = feval(func, x2);

% Iterative solution

while (x2 - x0) > tolx % (x2 – x0) is always positive

% Calculate minimum point of parabola

numerator = (x2^2 - x1^2)*fx0 - (x2^2 - x0^2)*fx1 + ...

(x1^2 - x0^2) *fx2;

denominator = 2*((x2 - x1)*fx0 - (x2 - x0)*fx1 + (x1 - x0)*fx2);

xmin = numerator/denominator;

% Function value at xmin

fxmin = feval(func, xmin);

% Select the next set of three points to construct new parabola

if xmin < x1

if fxmin < fx1

x2 = x1;

fx2 = fx1;

x1 = xmin;

fx1 = fxmin;

else

x0 = xmin;

fx0 = fxmin;

end

else

if fxmin < fx1

x0 = x1;

fx0 = fx1;

x1 = xmin;

fx1 = fxmin;

else

x2 = xmin;

fx2 = fxmin;

end

k=k+1;

end

fprintf(‘x0 = %7.6f x2 = %7.6f f(x0) = %7.6f f(x2) = %7.6f \n’, ...

x0, x2, fx0, fx2)

fprintf(‘x_min = %7.6f f(x_min) = %7.6f \n’,xmin, fxmin)

fprintf(‘number of iterations = %2d \n’,k)

MATLAB program 8.4

function f = proﬁtfunction(Q)

% Calculates the objective function to be minimized

494

Nonlinear model regression and optimization

8.2.3 Golden section search method

Bracketing methods for performing minimization are analogous to the bisection

method for nonlinear root ﬁnding. Bracketing methods search for the solution by

retaining only a fraction of the interval at each iteration, after ensuring that the

selected subinterval contains the solution. A bracketing method that searches for an

extreme point must calculate the function value at two different points in the interior

of the interval, while the bisection method and regula-falsi method analyze only one

interior point at each iteration. An important assumption of any bracketing method

of minimization is that a unique minimum point is located within the interval, i.e. the

function is unimodal. If the function has multiple minima located within the interval,

this method may fail to ﬁnd the minimum.

First, an interval that contains the minimum x* of the unimodal function must be

selected. Then

xðÞ¼

0 x



0 x



;



for all x that lie in the interval. If a and b are the endpoints of the interval, then the

function value at any point x

in the interior will necessarily be smaller than at least

one of the function values at the endpoints, i.e.

ðÞ

max faðÞ; fðbÞðÞ:

Within the interval ½a; b, two points x

< x

are selected according to a formula that

is dependen t upon the bracketing search method chosen.

The function is evaluated at the endpoints of the interval as well as at these two

interior points. This is illustrated in Figure 8.5.If

ðÞ

then the minimum must lie either in the interval x

; x

½or in the interval x

; b½.

Therefore, we select the subinterval ½x

; b for further consideration and discard the

subinterval a; x

½. On the other hand if

ðÞ

ain = 10e-6; % feed concentration of A (kmol/m^3)

p = 400; % price in US dollars per kg of product

c = 15; % operating cost per kg of product

k = 2; % forward rate constant (1/hr)

V = 12; % fermentor volume (m^3)

rho = 2.5; % density (kg/m^3)

MWB = 70000; % molecular weight (kg/kmol)

f = -((p - c)*Q*ain*MWB*(1 - 1/(1 + k*V/Q))*8000 - ...

4000* (8000*rho*Q)^0.6);

We call the optimization function from the command line:

parabolicinterpolation(‘proﬁtfunction’, [50 70], 0.01)

x0 = 59.456686 x2 = 59.456692 f(x0) = -19195305.998460 f(x2) =

-19195305.998460

x_min = 59.456686 f(x_min) = -19195305.998460

number of iterations = 12

495

8.2 Unconstrained single-variable optimization

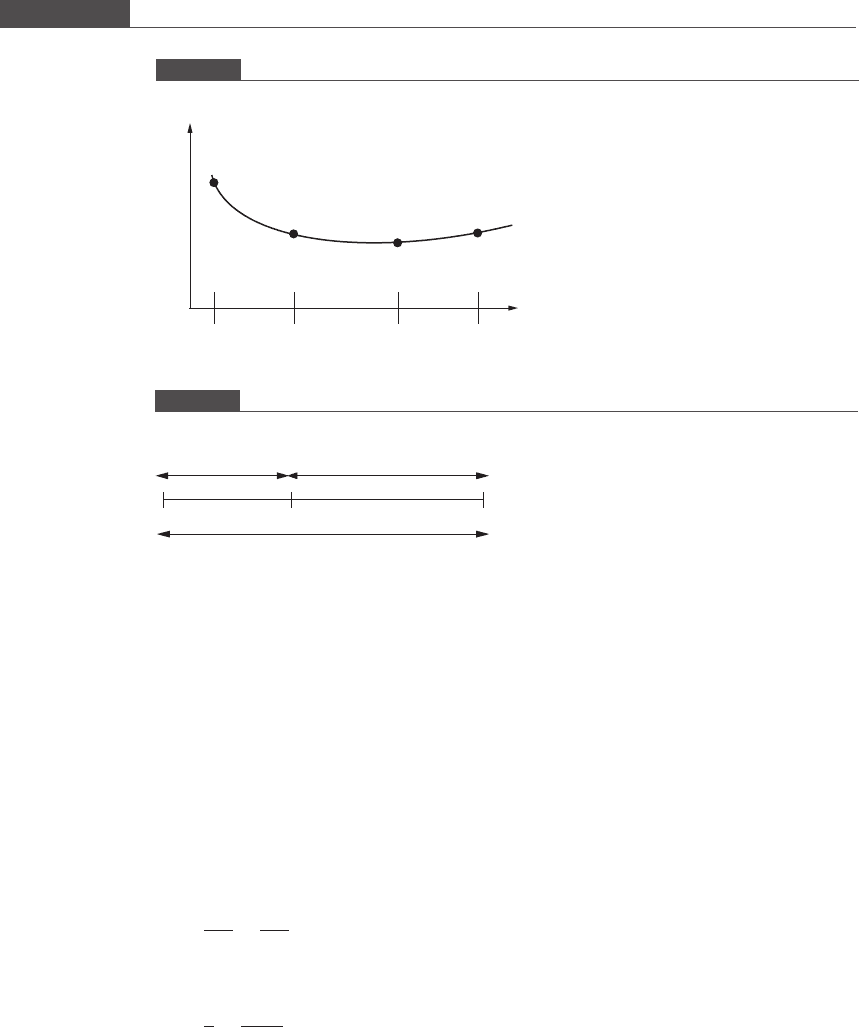
then the minimum must lie either in the interval a; x

½or in the interval x

; x

½.

Therefore, we select the subinterval ½a; x

 and discard the subinterval x

; b½.

An efﬁcient bracketing search method that requires the calculation of only one new

interior point (and therefore only one function evaluation) at each iterative step is the

golden section search method. This method is based on dividing the interval into

segments using the golden ratio. Any line that is divided into two parts according to

the golden ratio is called a golden section. The golden ratio is a special number that

divides a line into two segments such that the ratio of the line width to the width of the

larger segment is equal to the ratio of the larger segment to the smaller segment width.

In Figure 8.6, the point x

divides the line into two segments. If the width of the

line is equal to unity and the width of the larger segment x

b = r, then the width of

the smaller segment ax

=1–r. If the division of the line is made according to the

following rule:

1  r

(8:5)

then the line ab is a golden section and the golden ratio is given by 1=r.

Solving the quadratic equation r

þ r  1 ¼ 0(Equation (8.5)), we arrive at

r ¼ð

ﬃﬃﬃ

 1Þ=2orr ¼ 0:618034, and 1  r ¼ 0:381966. The golden ratio is given

by the inverse of r, and is equal to the irrational number ð

ﬃﬃﬃ

þ 1Þ=2 ¼ 1:618034. The

golden ratio is a special number and was known to be investigated by ancient Greek

mathematicians such as Euclid and Pythagoras. Its use has been found in architec-

tural design and artistic works. It is also arises in na tural patterns such as the spiral

of a seashell.

Figure 8.5

Choosing a subinterval for a one-dimensional bracketing search method

f (x)

Figure 8.6

Dividing a line by the golden ratio

1 – r

496

Nonlinear model regression and optimization