Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

2.6. Cause-Deleted Tables and Multiple Decrement 45

Chiang (1968) takes R to be simply the ratio of the age-speciﬁc rates for

the interval:

R =

(i)

. (2.6.5)

We will use the technique of Section 2.2 to make a slight improvement on

this. By expanding the µ

(i)

(x + t)andµ(x + t) in a Taylor series about the

midpoint of the n-year interval and then carrying through the integration,

we ﬁnd

R =



(i)

(x + t) dt



µ(x + t) dt

(i)

(x + n/2) + (n

/24)µ

(i)

(x + n/2)

µ(x + n/2) + (n

/24)µ



(x + n/2)

(2.6.6)

to second derivatives. Replacing the midperiod forces of mortality by the

age-speciﬁc rates, using a symmetric estimate of the second derivatives,

and then simplifying gives

R =

(i)





(i)

x+n

(i)

x−n

(i)

−

x+n

x−n



. (2.6.7)

The result would still hold with all M’s replaced by D’s where

(i)

is the

number of deaths observed from the ith cause between exact ages x and

x + n.

In the way such calculations are used, the life table of interest is that in

which one cause is deleted. For instance, on data for United States females

in 1964, the complete expectation of life for females is

=73.78 years; if

heart disease (CVR) is deleted, the

(−CVR)

=90.85 years (Preston, Key-

ﬁtz, and Schoen 1972, p. 771). Deletion of cancer gives

(−cancer)

=76.34

years. The gain by eradicating heart disease is 17.07 years; by eradicating

cancer, 2.56 years.

2.6.3 Multiple Decrement

The probability that a person will die of a certain cause in the presence

of other causes is presented in a multiple-decrement table. If the observed

number dying of the given cause is

(i)

and the life table number dying

of that cause is

(i)

, we want to ﬁnd how the life table deaths

are dis-

tributed among the several causes, given the observed distribution among

causes; given

,and

(i)

, we seek

(i)

. One way (Spiegelman

1968, p. 137) to make the calculation is

(i)

, (2.6.8)

but, as before, we try going one step in the reﬁnement of this.

46 2. The Life Table

Table 2.3. Part of a multiple-decrement table applying to cardiovascular disease,

comparing (2.6.9) with iterative and uncorrected methods, United States females,

1964

Age

(i)

x Iterative From (2.6.9) From (2.6.8)

25 65 64.80 64.71

50 1,067 1,067.56 1,066.41

75 10,173 10,175.53 10,165.27

We have by deﬁnition

(i)



p(x + t)µ

(i)

(x + t) dt



p(x + t)µ(x + t) dt

and applying the Taylor expansion used earlier results in

(i)





x+n

−

x−n

+2n





x+n

−

x−n

−

(i)

x+n

−

(i)

x−n

(i)



(2.6.9)

Table 2.3 shows that the correction in (2.6.9), as compared with using the

simple

(i)

[

(i)

], is triﬂing. We seem to have reached a point

at which it is usually immaterial whether the correction is made or not.

Nonetheless cases will arise where within an age group one cause is declining

and the others rising, and then correction 2.6.9 will bring improvement.

2.7 The Life Table as a Unifying Technique in

Demography

The painstaking development of a method for inferring probabilities from

observed rates is justiﬁed by the fact that the same problem arises in many

ﬁelds. The ordinary life table, for which the data consist of the number of

deaths and the exposed population, both by age, is only the best-known

example. Figure 2.2 shows some other applications.

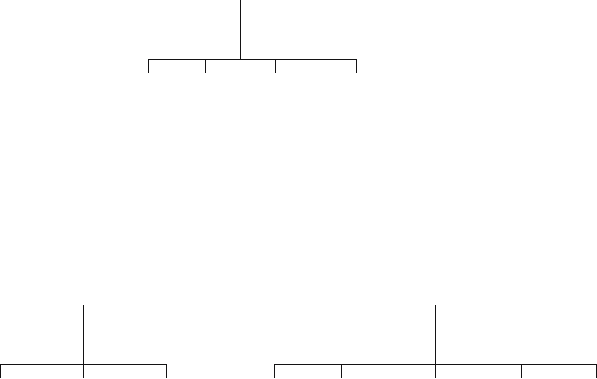
2.7. The Life Table as a Unifying Technique in Demography 47

Associated

(cause–deleted)

single–decrement

table recognizing

age and one

way of exit

Multiple–decrement

table recognizing

age and two or more

ways of exit

Cause

death

Leaving

school

Entering

labor

force

Combined table

following

individual

through

successive

companies

Migration Successive

grades at

school

with

dropouts

and

reentry

Labor

force

with

unemployment

and

retirement

Single

population,

nuptiality

and the

married

population

Successive

parities

Death

cause

Labor

force

and

death

First

marriage

and

death

Dropping

contraceptive

or becoming

pregnant

Figure 2.2. Some extensions of the life table.

The Matrix Model Framework

The life table, which formed the unifying technique for demographic anal-

ysis in Chapter 2, focuses on a very basic dichotomy (alive vs. dead) and

follows individuals as they age. This chapter introduces a diﬀerent, although

related, unifying framework—that of the population projection matrix. It

extends the dichotomy of the life table to consider individuals that diﬀer

according to many characteristics: age, sex, marital or employment status,

maturity, etc. Over each interval of time, each type of individual has not

only a probability of dying (on which the life table focuses) but also a

probability of moving to another category (as when an unemployed person

becomes employed) or of producing some number of new individuals (as by

reproduction).

Given these probabilities, one can compute the expected population

of each type of individual at the next time interval from that at the

present. This calculation is called a projection of the population. The in-

formation needed for a projection can most easily be written down in the

form of a matrix (called a population projection matrix) from which many

characteristics of population dynamics can be calculated.

We will introduce the matrix model framework in the context of age-

classiﬁed populations (here the relation to life table analysis is particularly

close) and then proceed to populations classiﬁed by other factors. The

ability of matrix models to classify individuals in many diﬀerent ways is

important to biologists because of the great diversity of plant and animal

life cycles. Human demographers may not worry about individuals entering

suspended animation, changing sex, shrinking instead of growing, or repro-

ducing by breaking into pieces, but all these things (and more) occur among

3.1. The Leslie Matrix 49

Age-class

(i)

Age (x)

Figure 3.1. The relation between the continuous age variable x,usedinthelife

table functions m(x) and l(x), and the discrete age classes i, used in the projection

matrix parameters P

and F

nonhuman species. Humans too have many important attributes in addi-

tion to age. Attempts to ﬁt these processes into the life table framework

have a strained and unsatisfactory feel, but matrix methods are equally

applicable to all of them (see Chapters 7 and 17, and AMD).

Matrix population models were introduced in the 1940s by Bernardelli

(1941), Lewis (1942), and especially Leslie (1945, 1948), whose name is

associated with them still. Leslie was an ecologist particularly interested in

populations of small mammals (Crowcroft 1991). In addition to his work

on matrix population models, he made the ﬁrst life table calculation of the

intrinsic rate of increase for any nonhuman species and made signiﬁcant

contributions to stochastic models and mark-recapture estimation. Matrix

models were largely neglected until the mid-1960s, when both ecologists

(Lefkovitch 1965) and human demographers (Lopez 1961, Keyﬁtz 1964,

Rogers 1966) rediscovered them.

3.1 The Leslie Matrix

We begin with a model for an age-classiﬁed population. We divide the

continuous variable age, which starts at 0, into a discrete set of age classes,

which start at 1. The scheme is shown in Figure 3.1. Age class i corresponds

to ages i − 1 ≤ x ≤ i. According to this convention, the ﬁrst age class is

number 1. Some authors number the ﬁrst age class as 0.

Our goal is to project the population from time t to time t+1. We assume

that the unit of time is the same as the age class width. We call this unit

the projection interval; its choice is one of the ﬁrst steps in constructing a

matrix model. Not surprisingly, a model that projects from year to year will

diﬀer from one that projects from month to month or decade to decade.

Suppose that the projection interval is one year, and that individuals

are classiﬁed into three age classes (0–1, 1–2, and 2–3 years). The state of

the population is described by a vector n(t), whose entries n

(t)givethe

numbers of individuals in each age class.

The individuals in age classes 2 and 3 at time t + 1 are the survivors of

the previous age classes at time t.Thatis,

(t +1)=P

(t)

(t +1)=P

(t),

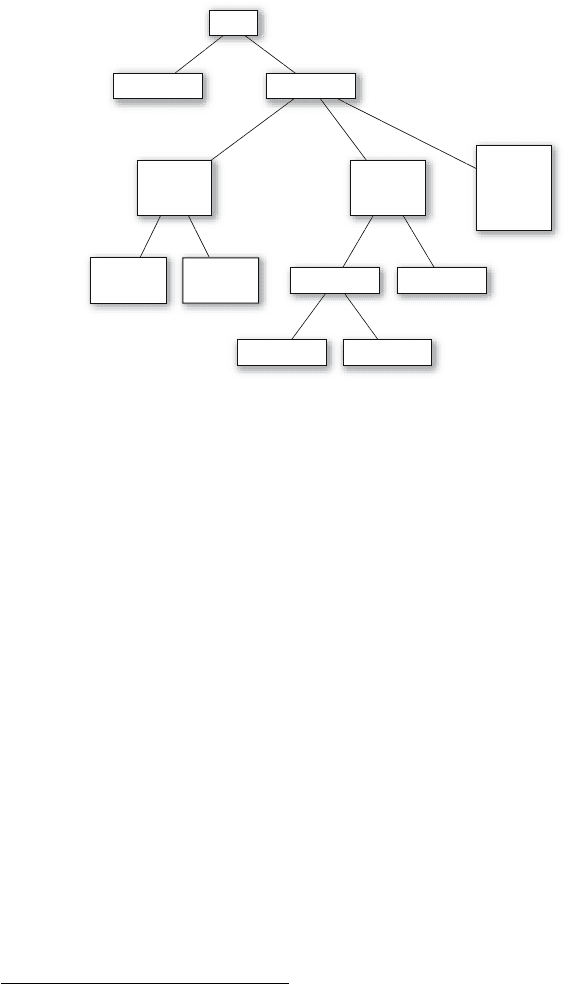
50 3. The Matrix Model Framework

Both

internally

and

externally

generated

Externally

generated

variability

Deterministic

Variable

Constant

Density-

dependent

Frequency-

dependent

Stochastic

Periodic Aperiodic

Internally

generated

variability

Figure 3.2. Classiﬁcation of matrix population models depending on the kinds of

variability included in the population projection matrix.

where P

is the probability that an individual of age class i survives for one

year.

The new members of age class 1 cannot be survivors of any other age-

class; they must have originated from reproduction. Thus we write

(t +1)=F

(t)+F

(t), (3.1.1)

where F

is the per-capita fertility

∗

of age class i, that is, the number of

individuals in age class 1, at time t + 1, per individual in age class i at time

These equations can be conveniently written in matrix form as

⎛

⎝

⎞

⎠

(t +1)=

⎛

⎝

0 P

⎞

⎠

⎛

⎝

⎞

⎠

(t) (3.1.2)

or, more compactly,

n(t +1)=An(t), (3.1.3)

where n is the population vector and A is the population projection matrix.

This special, age-classiﬁed version is often referred to as a Leslie matrix.It

is nonnegative (since negative elements would imply negative numbers of

∗

We use fertility to describe actual reproductive performance and fecundity to denote

the physiological potential for reproduction; in ecology the deﬁnitions are sometimes

reversed.

3.2. Projection: The Simplest Form of Analysis 51

individuals), with positive entries only in the ﬁrst row (fertilities) and the

subdiagonal (survival probabilities).

Matrix population models can be classiﬁed by the nature of the pro-

jection matrix A (see Figure 3.2). In the simplest case, the matrix is a

constant. We will spend a lot of time on this case, in spite of the unde-

niable fact that survival and reproduction are not constant. The resulting

model is a linear, time-invariant system of diﬀerence equations

n(t +1)=An(t). (3.1.4)

If A is not constant, it may vary because of external factors independent

of the population (e.g., weather), or because of changes in the internal state

of the population itself. A variable external environment leads to a linear

time-varying model

n(t +1)=A

n(t), (3.1.5)

where each element of A

may be a function of time. The variation may be

deterministic or stochastic; if deterministic, it may be periodic or aperiodic.

Variation due to the population yields a nonlinear model

n(t +1)=A

n(t), (3.1.6)

where each entry of A

may be a function of the population vector n.

Nonlinear models can be divided into density-dependent and frequency-

dependent categories (two-sex models are generally frequency-dependent;

MPM Chapter 17).

It is possible to combine environmental variation and density dependence

or frequency dependence, to yield a system of inhomogeneous nonlinear

equations

n(t +1)=A

n,t

n(t). (3.1.7)

As you might expect, such models are diﬃcult to analyze.

We will not explore time-varying or nonlinear models here, but they are

treated at length in MPM.

3.2 Projection: The Simplest Form of Analysis

One of the advantages of matrix models is that they are easy to implement

on a computer. Given an initial population n(0), you calculate the entries

in A

n(0),0

, taking into account whatever nonlinearities or time-variation

may be operating. Use this matrix to produce n(1). Repeat the procedure:

n(1) = A

n(0),0

n(0)

n(2) = A

n(1),1

n(1)

n(3) = A

n(2),2

n(2)

52 3. The Matrix Model Framework

and so on, as long as desired. It is an easy and instructive exercise to

program this repeated multiplication on a small computer (among other

things, writing a program guarantees that you understand the rules for

matrix multiplication). Here, we show the results of some simple projections

of this sort.

Example 3.1 A linear, time-invariant model

Consider the projection matrix

A =

⎛

⎝

015

.300

0 .50

⎞

⎠

. (3.2.1)

According to this matrix, the probability of surviving from the ﬁrst

age class to the second is P

=0.3, and the probability of surviving

from the second age class to the third is P

=0.5. Individuals in

the three age classes produce F

=0,F

=1,andF

= 5 surviving

oﬀspring per projection interval.

Figure 3.3 shows the results of applying this matrix to an initial

population vector

n(0) =

⎛

⎝

⎞

⎠

For the ﬁrst 15 time intervals, the abundances of the three age classes

ﬂuctuate irregularly, although there appears to be a slight upward

trend. Looking at the results over a longer time scale and on a log-

arithmic abundance scale, reveals that each age class (and thus the

total population) eventually grows exponentially at the same rate.

The relative proportions of the three age classes eventually converge

to constant values.

Example 3.2 Eﬀects of initial conditions

The results in Figure 3.3 are speciﬁc to the initial population n(0).

What if this initial population were changed? Figure 3.4 shows the re-

sult of 10 simulations, each with a diﬀerent, randomly selected initial

age distribution. All 10 eventually grow at the same rate and con-

verge to the same age distribution. They do not, however, all achieve

the same population size at any given time. One might suspect (given

some foresight about the concept of reproductive value, to be intro-

duced in Chapters 8 and 9) that this results from the timing of events

in the life cycle. An initial condition biased toward individuals in age

class 1 is at a disadvantage because these individuals must wait, with

an attendant probability of mortality, one time step before they begin

to reproduce and two time steps before they reach their maximum

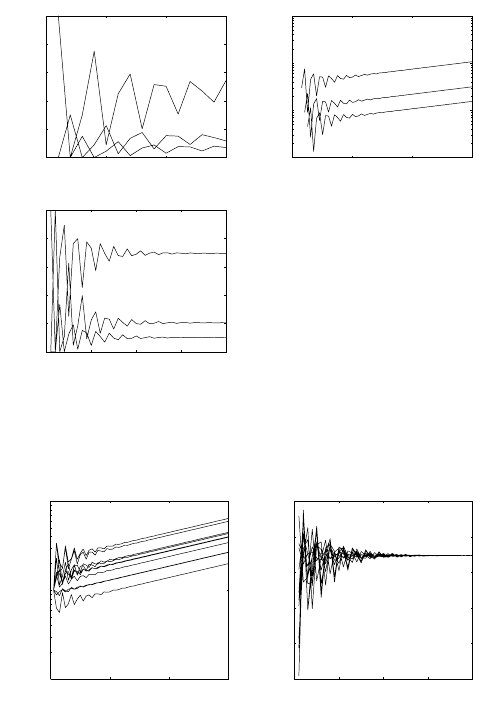
3.2. Projection: The Simplest Form of Analysis 53

0 5 10 15

0.2

0.4

0.6

0.8

Time

Numbers

0 20 40 60

−2

−1

Time

Numbers

0 10 20 30 40

0.2

0.4

0.6

0.8

Time

Proportions

Figure 3.3. Projection of an initial population consisting of a single individual in

age class 1, using the matrix in (3.2.1). Numbers on the line indicate age classes.

0 20 40 60

−1

Time

Total population

0 10 20 30 40

0.2

0.4

0.6

0.8

Time

Age−class 1 proportion

Figure 3.4. Projection of 10 randomly selected initial populations, all with the

same total size, using the projection matrix of (3.2.1).

fertility. An initial condition biased toward age class 3 has an ad-

vantage because these individuals reproduce at their maximum rate

immediately. Such a population has, and maintains, a head start over

the others.

Example 3.3 Eﬀects of perturbations

What happens if the entries in A are changed? Suppose that an envi-

ronmental stress reduces the survival or reproduction of one age class

by 10 percent, leaving all else unchanged. The results of these ﬁve

perturbations are shown in Figure 3.5. Reducing survival or fertility

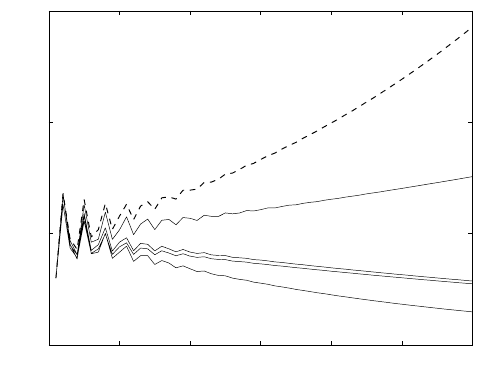
54 3. The Matrix Model Framework

0 10 20 30 40 50 60

Time

Total population

original

Figure 3.5. Projections of total population size, comparing the original projection

matrix of Figure 3.3 (dotted line) with the results of reducing each of the vital

rates by 10 percent.

reduces population growth rate (no surprise here), but where in the

life cycle the change happens makes a big diﬀerence. A 10 percent re-

duction in F

reduces the growth rate but leaves it positive. The same

reduction applied to F

, P

,orP

appears to drive the population to

extinction. It appears that population growth is most sensitive to a

proportional change in P

3.2.1 A Set of Questions

The preceding examples have posed the four fundamental questions of

demographic analysis.

Asymptotic analysis. A model describes a set of processes. Asymptotic

analysis asks what happens if those processes operate for a very long

time. What is the long-term behavior of the population? Does it grow

or decline? Does it persist or go extinct? Converge to an equilibrium,

oscillate, or do something more chaotic?

Ergodicity. The dynamics of a population depend not only on the model,

but also on the initial conditions. A model (or the population it

describes) is said to be ergodic if its asymptotic dynamics are inde-

pendent of initial conditions. Ergodic results are useful because they

imply that population patterns might reveal something about pro-

cesses rather than initial conditions. Many scientists, as opposed to