Keyfitz N., Caswell H. Applied Mathematical Demography
Подождите немного. Документ загружается.

2.2. Life Tables Based on Data 35
Thus (2.2.8) becomes
n
M
x
=
1
n
x+n
x
µ(a) da +
n
3
12
n
N
x
p
x +
n
2
µ
x +
n
2
, (2.2.9)
which after transposing provides the desired
x+n
x
µ(a) da as
x+n
x
µ(a) da = n
n
M
x
−
n
4
12
n
N
x
p
x +
n
2
µ
x +
n
2
. (2.2.10)
All that remains for the application is to express the first derivatives on
the right of (2.2.10) in terms of known quantities. One might make the
natural assumption that the slope within the interval x to x + n is given
by the difference between neighboring intervals:
p
x +
n
2
= −
n
N
x−n
−
n
N
x+n
2n
2
µ
x +
n
2
=
n
M
x+n
−
n
M
x−n
2n
,
(2.2.11)
and so the calculable value of l
x+n
/l
x
is
l
x+n
l
x
=exp
−
x+n
x
µ(a) da
=exp
−n
n
M
x
−
n
48
n
N
x
(
n
N
x−n
−
n
N
x+n
)(
n
M
x+n
−
n
M
x−n
)
=exp[−n(
n
M
x
+ C)] .
(2.2.12)
[We are grateful to James Frauenthal for his correction of the original ap-
proximation to p
(x + n/2) in (2.2.11), which had n rather than n
2
in the
denominator.]
The expression for l
x+n
/l
x
in (2.2.12) is the outcome of the search for
a life table that would accord with the data in the sense of having the
same underlying µ(x) as the observations, yet be calculable in one simple
step. It is equivalent to using the simple exponential l
x+n
/l
x
= e
−n
n
M
x
,
but first raising
n
M
x
by the quantity C =(
n
N
x−n
−
n
N
x+n
)(
n
M
x+n
−
n
M
x−n
)/48
n
N
x
, a product that is positive whenever the population is
declining with age and the death rate is rising.
The accuracy of (2.2.12) has been impressive in the tests so far done.
Applying it to Swedish males, 1965, at ages 20 to 65, for example, we found
that l
65
/l
20
differed by 0.00001 from the value obtained by interpolating to
fifths of a year separately for deaths and population, constructing the life
table in fifths of a year, and then reassembling into 5-year age groups. It
also differed by about 0.00001 from the more elaborate iterative life table
(Keyfitz 1968, Chapter 1).

36 2. The Life Table
Table 2.1. Example of life table calculation without iteration or graduation,
United States males, 1972
l
x+5
l
x
= exp[−5
5
M
x
−
5
48
5
N
x
(
5
N
x−5
−
5
N
x+5
)(
5
M
x+5
−
5
M
x−5
)] = exp[−5(
5
M
x
+ C)]
Correction to
5
M
x
; C =
l
x+5
l
x
=
5
q
x
=
Age
5
N
x
1000
1000
5
M
x
(
5
N
x−5
−
5
N
x+5
)(
5
M
x+5
−
5
M
x−5
)
48
5
N
x
e
−5(
5
M
x
+C)
1 −
l
x+5
l
x
x (1) (2) (3) (4) (5)
35 5458 3.017
40 5720 4.623 −0.0000058 0.97718 0.02282
45 5814 7.483 0.0000025 0.96326 0.03674
50 5616 11.367 0.0000388 0.94457 0.05543
55 4828 18.092 0.0000990 0.91306 0.08694
60 4192 27.483 0.0001667 0.87088 0.12912
65 3294 39.958 0.0003802 0.81735 0.18265
70 2330 59.770
In an age of computers ease of calculation is less important than it once
was, but nonetheless Table 2.1 is introduced to show the extreme simplicity
of the arithmetic.
The present method can be adapted to the ages at the beginning and
end of life. However, these ages involve data problems as well as rapidly
changing mortality rates. The reader is referred to Shryock and Siegel (1971,
Chapter 15), Wolfenden (1954), Keyfitz (1968, Chapter 1), or other sources
for ages under 10 and over 80.
A further point due to Kenneth Wachter and Thomas Greville is that
the derivative µ
(x + n/2) cannot strictly be estimated by (
n
M
x+n
−
n
M
x−n
)/2n, for the M’s are weighted averages of the µ’s and in a growing
population will always be too low. We can escape the difficulty by a second
iteration. When an approximate value has been found for the l
x
, we in effect
have an approximation to the unweighted
x
x−n
µ(a) da = −log(l
x
/l
x−n
),
and can enter this divided by n in place of the
n
M
x−n
.Inshort,wewould
substitute for
n
M
x+n
−
n
M
x−n
the quantity (1/n) log(l
x
l
x+n
/l
x−n
l
x
2
n
)
obtained on the first iteration.
The numerical effect can be judged from the following values obtained
from Table 2.1:
Age
n
M
x+n
−
n
M
x−n
1
n
log
l
x
l
x+n
l
x−n
l
x+2n
45 0.00674 0.00679
50 0.01061 0.01070
55 0.01612 0.01625
60 0.02187 0.02215
The differences
n
M
x+n
−
n
M
x−n
are in all cases too low, but the largest
discrepancy is about 1.25 percent. This means that our correction, itself
2.2. Life Tables Based on Data 37
of the order of 1 percent of
n
M
x
, would be raised by about 1 percent
on the iteration. Few users will regard this correction of the correction as
numerically important.
2.2.4 Greville and Reed–Merrell Methods Derived as Special
Cases
The generality of (2.2.10) can be demonstrated by applying it to derive a
well-known expression due to Greville (1943):
n
0
µ(x + t) dt = n
n
m
x
+
n
3
12
n
m
2
x
(log
n
m
x
)
, (2.2.13)
in terms of
n
m
x
, the life table death rate defined as
n
d
x
/
n
L
x
, where the
prime again signifies a derivative.
The demonstration starts by writing l(x)forp(x) in (2.2.10) and noting
that l
(x + n/2) = −l(x + n/2)µ(x + n/2). Thus, when
n
M
x
is replaced
with
n
m
x
and
n
N
x
with
n
L
x
(as though the data came from a stationary
rather than an increasing population), (2.2.10) becomes
n
0
µ(x + t) dt = n
n
m
x
+
n
4
12
n
L
x
l
x +
n
2
µ
x +
n
2
µ
x +
n
2
≈ n
n
m
x
+
n
3
12
n
m
xn
m
x
,
if we approximate l(x + n/2)/
n
L
x
by 1/n and µ(x + n/2) by
n
m
x
. Multi-
plying and dividing the correction terms on the right of the last expression
by
n
m
x
, and then using the fact that
n
m
x
/
n
m
x
=(log
n
m
x
)
, provides
Greville’s result (2.2.13).
Greville expressed his result as (2.2.13) to make use of the virtual con-
stancy of (log
n
m
x
)
through most ages and for most life tables. If this is
taken as (log
n
m
x
)
=0.096, then (2.2.10) becomes
n
0
µ(x + t) dt = n
n
m
x
+0.008n
3
n
m
2
x
,
so that the survival probability is
l
x+n
l
x
=exp
−
n
0
µ(x + t) dt
=exp(−n
n
m
x
− 0.008n
3
n
m
2
x
), (2.2.14)
which is the expression derived empirically by Reed and Merrell (1939).
The tabulation of (2.2.14) included in the Reed–Merrell paper has been
used more extensively than any other system for making a life table. It was
indeed convenient in the days before computers were available, but it rests
on two gross assumptions: (1) that the observed population provides the
stationary age-specific rates of the life table; and (2) that the same form,
0.008n
3
n
m
2
x
, serves to correct the
n
m
x
for all ages and for any life table.
The simple expression 2.2.12 avoids both these restrictions.
38 2. The Life Table
2.2.5 Bounds on Error
All of the above discussion would be superfluous if there were some cor-
rect way to make a life table. Unfortunately ignorance of the distribution
of population and deaths within each 5-year age interval has to be com-
pensated for by more or less arbitrary assumptions. For most populations
single years are sought from the respondent, but the information is pub-
lished only in 5-year intervals, a wise policy on the part of the statistical
authorities in view of the inaccuracy of individual reporting. Whether the
age intervals 5 to 9, 10 to 14, and so on, are the best is another matter;
concentration on multiples of 5 causes these to understate the mean age in
comparison with 3 to 7, 8 to 12, and so on.
The deaths and population can of course be interpolated so finely that
the outcome is unique whatever the interpolation formula. Whole years or
fifths of a year are sufficiently fine since the uncertainty of converting
n
M
x
into
n
q
x
decreases with the cube of the interval n. To be convinced of this,
compare two formulas generalized from (2.2.1) and (2.2.6), respectively:
n
q
x
=1− e
−n
n
M
x
and
n
q
x
=
n
n
M
x
1+(n/2)(
n
M
x
)
.
Expanding these in powers of n gives
1 − e
−n
n
M
x
= n
n
M
x
−
n
2
n
M
2
n
2!
+
n
3
n
M
3
x
3!
−···
and
n
n
M
x
1+(n/2)(
n
M
x
)
= n
n
M
x
−
n
2
n
M
2
x
2
+
n
3
n
M
3
x
4
−···.
The two agree up to the term in n
2
; then the exponential is lower by the
difference n
3
n
M
3
x
/12, disregarding higher-order terms. Thus the difference
in single years is approximately 1/125 of the difference in 5-year age groups.
But interpolation cannot provide a uniquely correct table, since it de-
pends on a choice of formula that is inevitably arbitrary. Iterative methods
also make various assumptions; one such method (Keyfitz 1968, p. 19)
supposes local stability—that the observed population has been increasing
uniformly within 5-year age intervals. The method of the present chap-
ter avoids both interpolation and iteration; its arbitrariness involves the
derivatives for the correction to l
x+n
/l
x
= e
−n
n
M
x
in (2.2.12), calculated
by stretching a straight line between the age intervals below and above
the one of interest, and experimenting has shown that different ways of
calculating the first or higher derivatives make little difference.
Lacking knowledge of the true life table, can we at least set bounds on
it? We can, establishing the higher bound by supposing the population
(and corresponding deaths) within the age group x to x + n to be all
concentrated at the low end. This would mean that the observed death rate
really refers to exact age x, so that what we call
n
M
x
is not an average of

2.3. Further Small Corrections 39
the rates µ(t)fromx to x + n, but is really µ(x). If, on the other hand, the
population is all concentrated at the high end, what we observe as
n
M
x
is really µ(x + n). These two opposite possibilities furnish the extreme
bounds; the
n
M
x
, and hence the l
x
column derived from it, could refer
to a population n/2 years younger than stated, or to a population n/2
years older. No logic can demonstrate that either such freak situation is
impossible, improbable though it may be in even a small population.
For the United States life table of 1967,
o
e
15
for males was 54.22 years. On
the above-mentioned argument this number could really represent anything
from
o
e
12
1
2
to
o
e
17
1
2
. Since at these ages
o
e
x
is declining by about 4.75 years
per 5 years of age, the true
o
e
15
could lie approximately in a range from
54.22 − 4.75/2to54.22 + 4.75/2, or from 51.84 to 56.60. Such a range is
too wide to be of much practical interest, and yet it is hard to see the logic
by which one can narrow the possibilities. Not only is there no correct life
table, but also there is not even a simple way of establishing a realistic
range of error, analogous to the 0.95 confidence interval that is used where
a probability model applies.
A lower bound to the error of the life table is obtained by supposing that
individuals die independently at random, each with probability
n
q
x
for his
age x. The expression for this is easily derived (Keyfitz 1968, p. 341, is a
secondary source with references). But such an error seems as far below
the true error as that of this section is above.
2.3 Further Small Corrections
The method of calculating a life table expressed in (2.2.12) has proved
highly satisfactory in practice, giving negligible departure from graduated
life tables and from iterated tables, without requiring either graduation
or iteration. However, it depends on solving basic equation 2.2.2 for the
integral for µ(a), and therefore some readers may wish to look more closely
at the rationale of (2.2.2).
Measure of Exposure. A diagram, due to Lexis (1875), that displays the
population by age and time will help in this. Each individual at any moment
is represented by a point; the collection of points for any individual is his
life line through time; the end of the line is at the moment and age of his
death.
Figure 2.1 shows the beginning and end of the year 1967, for which the
observations are being analyzed, as horizontal lines, and ages 65 and 70 as
vertical lines. In the rectangle ABCD, 122,672 males lines come to an end
for the United States in 1967. We do not quite know how many lines are
in the rectangle, but it was estimated that 2,958,000 crossed the horizontal
line for July 1, 1967, and this number,
5
N
x
in general, is commonly used
to estimate exposure; it would be better to use person-years.
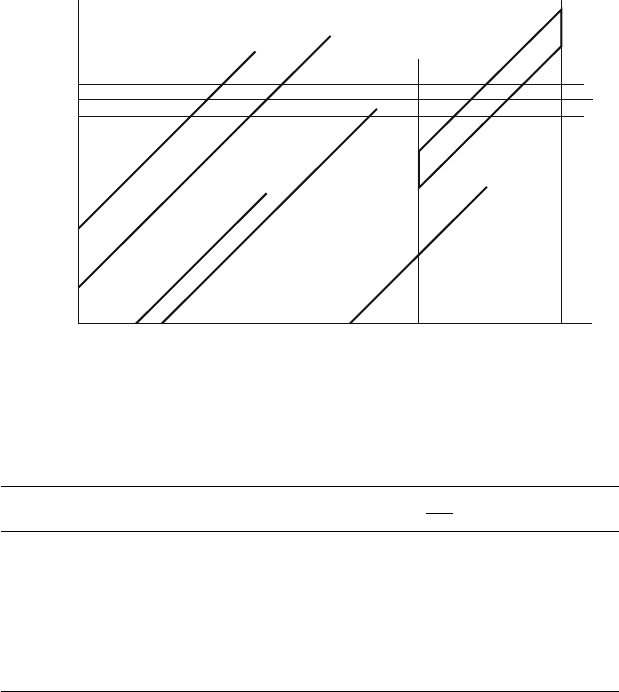
40 2. The Life Table
Time
Age
Jan. 1, 1968
Jan. 1, 1967
65 70
A
D
A′
D′
B′
C′
B
C
Figure 2.1. Living and dying population displayed on plane of age and time in
Lexis diagram.
Table 2.2. Population and deaths, United States males, 1972, along with their
first and second differences
Age Population Deaths
x
5
N
x
∆
5
N
x
∆
2
5
N
x
5
D
x
5
M
x
=
5
D
x
5
N
x
∆
5
M
x
∆
2
5
M
x
50 5,616,000 63,838 0.011367
−788,000 0.006725
55 4,828,000 152,000 87,348 0.018092 0.002666
−636,000 0.009391
60 4,192,000 −262,000 115,208 0.027483 0.003083
−898,000 0.012474
65 3,294,000 −66,000 131,620 0.039957 0.007339
−964,000 0.019813
70 2,330,000 218,000 139,264 0.059770 0.008784
−746,000 0.028597
75 1,584,000 84,000 139,974 0.088367 0.006392
−662,000 0.034989
80 922,000 113,734 0.123356
Other directions of improvement, which the reader may wish to investi-
gate, include the use of higher derivatives in the Taylor expansion of (2.2.8),
and better ways of estimating the first derivative. Differences useful in ap-
proximating to the derivatives are provided in Table 2.2. Their effect on
the correction C of Table 2.1 will be found to be slight.
2.4 Period and Cohort Tables
We have noted that, although in each age group the life table estimates how
much a cohort will diminish by death, the probabilities for the several ages
are chained together in a way that can represent only the period for which
the data are gathered. The result describes what is sometimes referred to
as a synthetic cohort.

2.5. Financial Calculations 41
To follow genuine cohorts we can chain together the survival probabilities
of a sequence of periods. In 1919–21 the chance of survival for 5 years for a
male just born was 0.87420 (Keyfitz and Flieger 1968, p. 142); in 1924–26
the chance of survival from age 5 to age 10 was 88,574/89,600 = 0.98855
(p. 144); in 1929–31 from age 10 to age 15 it was 88,814/89,587 = 0.99137
(p. 145); and so on. Chaining these together gives
l
0
= 100,000,l
5
=87,420,l
10
=86,419,l
15
=85,673 etc.,
as an estimate of survivorship for a real child born about 1917. Portrayal
on a Lexis diagram suggests that the result is a reasonably good ap-
proximation, provided that mortality does not change abruptly over time.
Refinements of the cohort calculation are being carried out by Michael
Stoto, who has improved estimates of population and deaths in the lozenge
A
B
C
D
of Figure 2.1.
2.5 Financial Calculations
Demography has a part of its origin in actuarial calculations, just as
probability sprang from gambling consultancies. The center of gravity of
demography has shifted far from the insurance business, but at least the
style of actuarial calculations is worth exhibiting here, perhaps as a small
contribution toward bringing these disciplines closer together again.
2.5.1 Single-Payment Annuity and Insurance
The present value of a life annuity of 1 dollar per year, paid continuously
starting from age x of the person, is equal to
1
l
x
ω−x
0
l(x + t) dt =
o
e
x
dollars, if money carries no interest. It needs no mathematics to see that
the expected number of dollars that a person will receive at the rate of 1
for each year of life is the same as the expected number of years he has to
live. If money carries interest continuously compounded at annual rate i,
apaymentt years from now has a present value of e
−it
; hence the present
value of the annuity is
a
x
=
1
l
x
ω−x
0
e
−it
l(x + t) dt (2.5.1)
dollars. Similarly the present value of an assurance of 1 dollar on a life now
aged x must be
A
x
=
1
l
x
ω−x
0
e
−it
l(x + t)µ(x + t) dt (2.5.2)

42 2. The Life Table
dollars, which is the same as (2.5.1) except for the factor µ(x + t)inthe
integrand. [Show that, if interest is zero, A
x
= 1, corresponding to the fact
that dying is inevitable. Show also that, if i>0, A
x
> exp(−i
o
e
x
).]
2.5.2 Annual Premiums and Reserves
To find the annual premium P
x
, note only that the annuity of premiums
must cover the assurance; that is to say, the quantities P
x
a
x
and A
x
must
beequal.HencewehaveforthepremiumP
x
= A
x
/a
x
or, written out in
full,
P
x
=
ω−x
0
e
−it
l(x + t)µ(x + t) dt
ω−x
0
e
−it
l(x + t) dt
. (2.5.3)
In the early years of the policy, claims will be less than premiums, and
a reserve will accumulate that will be drawn on in later years. After the
policy has been in force for y years the present value of the claims will be
A
x+y
, and cannot be covered by the present value of the premiums P
x
a
x+y
,
a smaller quantity for the ages at which mortality is rising; the difference
A
x+y
− P
x
a
x+y
, is the reserve prospectively needed.
2.6 Cause-Deleted Tables and Multiple Decrement
If a person dies of one cause, he cannot die at some later time of another;
the literature speaks of competing causes of death. Since dying of a given
cause avoids exposure to other causes, if we wish to know what the mor-
tality from these other causes would be if the given cause were deleted,
we need upward adjustment to the observed rates. Over a finite interval
of time or age it would be incorrect to delete a cause simply by neglecting
all deaths from this cause and calculating the life table from the remaining
deaths; such a procedure would give too low mortality from the remaining
causes. We need an estimate of exposed population that does not include
persons dead of the deleted cause. To make the estimate it is customary to
assume that the several causes act independently.
2.6.1 Dependence of Causes of Death
Think of a watch or other machine having parts and operating only as long
as all the parts are functioning. Each part has its own life table; the chance
that the ith part will operate for x years is
¯
l
(i)
(x), calculated without
reference to other parts. Then the chance that the watch will still be going

2.6. Cause-Deleted Tables and Multiple Decrement 43
x years after its birth is
l(x)=
¯
l
(1)
(x) ·
¯
l
(2)
(x) ···
¯
l
(n)
(x), (2.6.1)
a statement true if the mortality of each of the parts is unaffected by its
incorporation in the watch. Then, if
−
1
¯
l
(i)
(x)
d
¯
l
(i)
(x)
dx
= −
d log
¯
l
(i)
(x)
dx
= µ
(i)
(x),
it follows by taking logarithms and differentiating in (2.6.1) that
µ(x)=µ
(1)
(x)+µ
(2)
(x)+···+ µ
(n)
(x). (2.6.2)
The additivity of the instantaneous death rates follows from the multiplica-
tivity of the survivorships.
We can think of many ways in which these conditions would not be
fulfilled. The watch might keep going with one part defective but break
down when two are defective. Or else the weakening of one part might put
a strain on other parts; the watch would become “sick,” and its death might
ultimately be attributed to one of the parts that was so subjected to strain
rather than to the part that became weak in the first place. There is no
limit to the number of ways in which independence could be lost.
The parts of the watch might be said to resemble the parts of a person,
and these would be independent if it could be said that he dies if his
liver fails, or if his heart fails, and so on, and these were unrelated. The
probability of each organ continuing to function might be thought of as the
¯
l
(i)
(x) given in life tables showing the net probabilities of survival for the
several causes. Unfortunately for this argument, human parts depend on
one another more than do watch parts; separate life tables for the various
organs, as though they were interchangeable, are to this degree artificial.
In addition to interrelations of parts, selection operates: the persons who
die in skiing accidents are probably healthier on the average than the gen-
eral population; therefore, if precautions that reduced the number of fatal
accidents were introduced at ski resorts, the death rate from other causes
would also be lowered. The nature of such dependencies is extremely diffi-
cult to establish. As long as we know only that A died of heart disease, B of
kidney failure, and so on, nothing can be said about what would happen if
one of the causes was reduced or eliminated. Faced with no evidence on the
nature of dependencies, it is conventional to treat each cause as indepen-
dent of the others. If parts (of a person or a watch) looked weak or had other
clear symptoms before they failed altogether and brought the machine to
a stop, and if such signs were present exactly y years before they would
prove fatal, then something better could be done regarding dependencies.
But even the most conscientious medical tests pre- and postmortem hardly
provide such information.
It looks as though the analysis of interdependencies of the several organs
will have to await further data. One kind of relevant data will become avail-

44 2. The Life Table
able when parts are commonly and safely replaced or interchanged among
individuals. At present, however, such a possibility belongs to science fiction
rather than to demography.
2.6.2 Method of Calculation
If all causes but the ith were removed, what would be the probability of
surviving? To answer this without further data we suppose that the several
causes act independently of one another, that is to say, that their forces of
mortality are additive:
µ
(i)
x
+ µ
(−i)
x
= µ
x
, (2.6.3)
where µ
(i)
is the mortality due to the ith cause, and µ
(−i)
that due to all
other causes. If the survival probability with only the ith cause acting is
¯
l
(i)
x
, we have from (1.6.5) and the additivity of the µ
(i)
x
, as a converse of
the argument leading to (2.6.2),
l
x
=
¯
l
(i)
x
¯
l
(−i)
x
.
Thus essentially the same argument can start with the additivity of the
µ
(i)
x
and infer the multiplicativity of the
¯
l
(i)
x
, or else start with the latter as
we did in (2.6.1).
Now expression 1.6.5 applies to the
¯
l
(i)
x
just as it does to the l
x
; hence, as
pointed out by Jordan (1952, p. 258) and Chiang (1968, p. 246), we have
−log
¯
l
(i)
x+n
¯
l
(i)
x
=
n
0
µ
(i)
(x + t) dt
=
⎡
⎢
⎢
⎣
n
0
µ
(i)
(x + t) dt
n
0
µ(x + t) dt
⎤
⎥
⎥
⎦
n
0
µ(x + t) dt
= R
n
0
µ(x + t) dt,
say, and, on multiplying by −1 and taking exponentials of both sides,
¯
l
(i)
x+n
¯
l
(i)
x
=
l
x+n
l
x
R
. (2.6.4)
Once the ordinary life table from all causes together is available, all we need
do is raise its survivorships to the powers represented by the R’s; each is
the ratio for an age group of the integral of the force of mortality for the
ith cause to the corresponding integral for all causes.
