Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

Markov Chains for Individual Life

Histories

The passage of an individual through its life cycle, from birth to death,

is marked by various notable events. Some, like maturation or mating or

reproduction, may be optional. Others, like death, are inevitable. A matrix

model contains a great deal of information (or, equivalently, makes many

strong assertions) about these events, their probabilities, and the sequences

in which they tend to occur. This chapter shows how to extract some of

the implications of these assertions. For example, what is the probability of

surviving from birth to maturity in a model where individuals may reach

maturity by many pathways? What is the average time required to mature?

What is the probability of experiencing an event (e.g., a disease, or attack

by a predator) before maturing, or before dying? Such questions can be

answered by describing the individual life cycle as a Markov chain. The re-

sults provide ways to calculate age-speciﬁc parameters from stage-classiﬁed

models.

11.1 A = T + F: Decomposing the Matrix

Most life cycles permit a distinction between the transitions of living indi-

viduals and the production of new individuals. Thus the projection matrix

can be written

A = T + F, (11.1.1)

where T describes transitions and F describes reproduction. The element

of F is the expected number of type i oﬀspring produced by an individual

246 11. Markov Chains for Individual Life Histories

in stage j. The element t

of T is the probability that an individual in stage

j at time t is alive and in stage i at time t + 1. This decomposition has

been applied by Cochran and Ellner (1992) to density-independent models

and Cushing (1988, 1997, Cushing and Yicang 1994) to density-dependent

models.

11.1.1 The Life Cycle as a Markov Chain

We will describe the movement of an individual through its life cycle as a

Markov chain. The matrix T describes part of this movement, but it must

be augmented by adding an extra state, “dead.” If there are s stages, the

result is an s + 1 dimensional Markov chain with transition matrix

∗

P =



m 1



of dimension



s × s

s × 1

1 × s 1 × 1



. (11.1.2)

Here, m

=1−



is the probability of death for stage j. State s +1

(death) is an absorbing state; once an individual enters this state, it never

leaves.

There is a sizeable literature on Markov chain models for movement

of individuals among social and occupational classes (e.g., Bartholomew

1982), some of which has been applied to demography (see Section 10.5).

Feichtinger (1971, 1973) applied these methods to age-classiﬁed models

with multiple absorbing states, ﬁrst marriage models, and models for mul-

tiple classiﬁcations (age and parity, age and marital status). Cochran and

Ellner (1992) independently used Markov chains in an analysis of stage-

classiﬁed models. They also considered cases where F is divided into

separate matrices representing birth and ﬁssion.

The states in an absorbing Markov chain can be divided into two sets: a

set T of transient states and a set A of absorbing states; in this model

T = {1, 2,...,s}

A = {s +1}.

We will denote the number of elements in the set A by |A| (this is the car-

dinality of A). At this point, |A| = 1, but later we will add more absorbing

states. We assume (it is implicit in calling the set T transient) that there

is a pathway from each of the states in T to one of the states in A.That

is, there are no immortal stages in the life cycle. If there were, they would

appear as another set of absorbing states.

∗

To emphasize the parallel with population projection matrices, P has been written

as a column-stochastic matrix. Many texts on Markov chains would write it as a row-

stochastic matrix, equivalent to the transpose of the matrix listed here. Either way is

OK; just be careful to get the proper orientation of formulae presented in such texts.

11.1. A = T + F 247

Let x be a column vector giving the probability distribution of states,

where 0 ≤ x

≤ 1and



=1.Then

x(t +1)=Px(t) (11.1.3)

and

x(t)=P

x(0), (11.1.4)

where





t−1

n=0



. (11.1.5)

Our assumption that it is possible to reach the state “dead” from every

state in T guarantees that the dominant eigenvalue of T is strictly less

than 1; thus lim

t→∞

= 0 (Iosifescu 1980, Theorem 2.2). Thus (11.1.3)

leads to the basic result on absorbing Markov chains: No matter what the

initial probability distribution, the probability of the system being in any

state other than an absorbing state eventually approaches zero.

Example 11.1 Markov-chain decomposition for killer whales

The killer whale life cycle graph is given in Figure 3.10. Using vi-

tal rates estimated for the resident population in coastal waters of

Washington and British Columbia (Brault and Caswell 1993), the

decomposition of A yields

T =

⎛

⎜

⎝

0000

0.9775 0.9111 0 0

00.0736 0.9534 0

000.0452 0.9804

⎞

⎟

⎠

(11.1.6)

F =

⎛

⎜

⎝

00.0043 0.1132 0

00 00

⎞

⎟

⎠

. (11.1.7)

Because only one kind of oﬀspring is produced, the fertility matrix F

contains only a single nonzero row. The transition matrix is

P =

⎛

⎜

⎝

0000

0.9775 0.9111 0 0

00.0736 0.9534 0

000.0452 0.9804

0.0225 0.0153 0.0014 0.0196 1.0000

⎞

⎟

⎠

. (11.1.8)

Example 11.2 From school to work.

Some of the considerations just mentioned can be illustrated by a

model of the school population and its emergence into the labor force

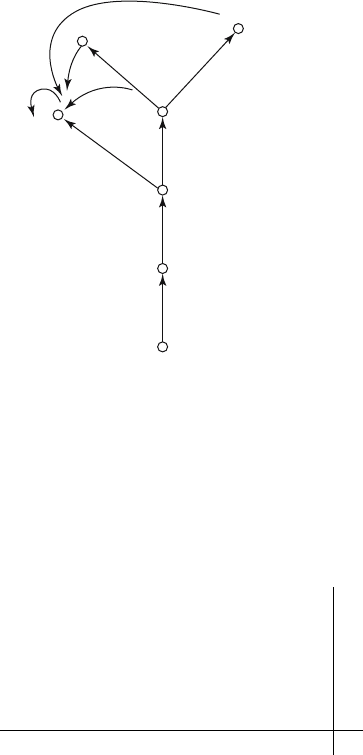
248 11. Markov Chains for Individual Life Histories

Technical

School –

grades 9 to 12

School –

grades 5 to 8

School –

grades 1 to 4

Preschool

College

Labor

force

Figure 11.1. Graph of progress through school system and points of emergence

into the labor force, along with corresponding matrix A, disregarding mortality

and repeating; projection interval = 4 years.

(Keyﬁtz 1977). Consider only the ﬂows portrayed in the graph of

Figure 11.1. We ignore mortality, but in this model stage N

,the

labor force, is an absorbing state. The transient states are N

–N

.In

this case, there is no reproductive process, and the transition matrix

P =

⎛

⎜

⎝

00 0 0 00

10 0 0 00

01 0 0 00

00 p

000

00 0 p

000

00 0 p

000

001− p

1 − p

− p

111

⎞

⎟

⎠

(11.1.9)

11.1.2 The Analysis of Absorbing Chains

So far we have only stated the obvious: if every individual can die, every

individual eventually will die. Now we want to know what happens to

individuals en route to that end. The results summarized here are standard

in Markov chain theory; see Iosifescu (1980, Chap. 3) or Kemeny and Snell

(1976, Chap. 3) for full treatments.

Notation alert.IfX is any matrix, then X

is the matrix with the

diagonal of X on its diagonal, and zeros elsewhere. The row sums of X are

Xe, and the column sums are e

X,wheree is a column vector of ones.

11.1. A = T + F 249

11.1.2.1 The Fundamental Matrix

The (i, j) entry of the matrix T

is the probability that an individual in

stage j at time 0 will be in stage i at time t,fori, j ∈T. Since absorption

is certain, these probabilities eventually decay to zero. But an individual

will visit various transient states, various numbers of times, before absorp-

tion happens. Let ν

be the number of visits to transient state i before

absorption, given that the individual starts in state j. The expected values

of the ν

are given by a matrix



E (ν

)



= I + T + T

+ ··· (11.1.10)

=(I − T)

−1

(11.1.11)

≡ N. (11.1.12)

The matrix N is called the fundamental matrix of the Markov chain.

The second moments of the ν

are





=(2N

− I) N (11.1.13)

(Iosifescu 1980). Thus the variance of the number of visits to each state is

given by the matrix



V (ν

)



=(2N

− I) N − N ◦ N, (11.1.14)

where ◦ denotes the Hadamard, or element-by-element, product.

The fundamental matrix provides information about the time to absorp-

tion (i.e., to death). Let the time to absorption, starting in transient state

i,beη

. The mean of η

is the sum of column j of the fundamental matrix

N (i.e., the number of visits to all the transient states)



E (η

) ··· E (η

)



= e

N. (11.1.15)

Iosifescu shows that the second moments of the η

are given by



··· E



= e

N (2N − I) . (11.1.16)

Thus the variance of time to absorption can be written



V (η

) ··· V (η

)



= e

− N

− e

N ◦ e

N. (11.1.17)

We can calculate not only the mean but the complete probability distri-

bution of the η

. The entries of T

give the probabilities of being in each

of the transient states at time t. Thus the sum of column j of T

is the

probability that absorption has not occurred by time t, starting from state

j.Thus



P [η

>t] ··· P [η

>t]



= e

. (11.1.18)

250 11. Markov Chains for Individual Life Histories

Since P [η

= t]=P [η

>t− 1] − P [η

>t], we obtain the probability

distribution for the times to absorption



P [η

= t] ... P [η

= t]



= e

t−1

− T

). (11.1.19)

11.1.2.2 Probabilities of Absorption

So far we have assumed only a single absorbing state (death). It is some-

times useful to consider models with multiple absorbing states, in which

case

P =



M I



, (11.1.20)

where M is a matrix whose entries m

give the probability of moving from

state j ∈T to the kth absorbing state in A. Every individual will end up

in an absorbing state, but which absorbing state is uncertain. We would

like to calculate the probabilities

= P [absorption in k|starting in j]1≤ k ≤|A|,j∈T. (11.1.21)

We know that if the system starts in transient state j it spends an average

of n

time steps in transient state i (where i ∈T). At each of these time

steps, the probability of moving to the kth absorbing state is m

.Thus



i∈T

1 ≤ k ≤|A| (11.1.22)

or, in matrix notation

B = MN. (11.1.23)

11.1.2.3 Probabilities Conditional on Absorption

If more than one absorbing state exists, we can calculate probabilities con-

ditional on which of those states an individual ends up in. For example,

we might describe mortality and emigration as absorbing states. We could

compare the properties (e.g., mean time before leaving the population) of

individuals that emigrate versus those that die before emigrating. We do

this by creating a new transition matrix, conditional on absorption in a

particular state.

Suppose we condition on absorption in the kth absorbing state. The state

space of the resulting Markov chain is the set T of transient states plus the

kth absorbing state. The transition matrix for this new conditional Markov

chain is

(c)



(c)



, (11.1.24)

11.2. Lifetime Event Probabilities 251

where the superscript c denotes the conditional chain. Bayes’ theorem

†

implies that the conditional probabilities can be written in terms of the

matrix M and the matrix B calculated from P:

(c)

(11.1.25)

(c)

= m

(11.1.26)

or, in matrix notation,

(c)

= DTD

−1

, (11.1.27)

where, letting b

k·

denote the kth row of B,

D = diag(b

k·

⎛

⎜

⎝

⎞

⎟

⎠

. (11.1.28)

The fundamental matrix for the conditional chain is

(c)

= DND

−1

. (11.1.29)

It can be used like any fundamental matrix.

We turn now to several important applications of these results.

11.2 Lifetime Event Probabilities

At any stage in its life cycle, an individual is embarking on a developmental

process that will eventually end in death. At each step of that process, the

individual experiences the risk of various events (e.g., contracting a disease,

or attack by a predator). The probability that an event occurs at least once

in the individual’s lifetime may be of interest in a variety of contexts. For

example:

• The plant Lomatium grayi is attacked by a moth called Depressaria

multiﬁdae. Lomatium grows through a series of size classes, alter-

nating between vegetative and ﬂowering condition. The probability

of attack by Depressaria is stage-dependent. Thompson and Moody

(1985) wanted to know the probability that a new seedling will be

attacked by the moth at least once during its lifetime. They inter-

pret this probability as a measure of the “apparency” of the plant to

its herbivore. It has been suggested that apparency should determine

the type of chemical defenses that a plant deploys against a herbivore

(Feeney 1976).

†

For any two events X and Y , P [X |Y ]=P [X and Y ]/P[Y ], provided that P [Y ] > 0.

252 11. Markov Chains for Individual Life Histories

• The U.S. Department of Justice has calculated the probability that

a 12-year-old American will experience certain kinds of violent crime

in his or her lifetime (Koppel 1987). The probabilities were 0.83 for

all types of violent crime, 0.99 for personal theft, 0.74 for assault,

0.30 for robbery, and 0.08 for rape (the latter ﬁgure for women).

These lifetime probabilities are presented as better measures of the

true risk of these crimes than annual incidence statistics (“If the earth

revolved around the sun in 180 days, all our annual crime rates would

be halved, but we would not be safer.” Koppel 1987)

• Bone fractures are a signiﬁcant health risk to postmenopausal women.

Cummings et al. (1989) found that the lifetime probability of hip

fracture for a 50-year-old U.S. woman was 0.156. The corresponding

probabilities for wrist fractures and atraumatic vertebral fractures

were 0.15 and 0.32. Combining these probabilities with estimates of

the mortality due to these injuries, they concluded that the lifetime

risk of death from hip fracture was comparable to that from breast

cancer. Such comparisons might be useful in comparing the risks and

beneﬁts of therapies designed to reduce osteoporosis.

In each of these cases, the lifetime probability is aﬀected by both the risk

of the event and the demography. The lifetime probability of hip fracture

could be lessened by reducing the risk of falling (e.g., by studying t’ai chi

chuan; Wolf et al. 1996) or by increasing mortality, so that fewer women

survive to ages where falls are more frequent. The former strategy is ob-

viously preferable, but in more complex life cycles the choices might be

less plain. Lomatium grayi might, for example, want to consider whether it

should try to prevent Depressaria attack, or adjust its life cycle to spend

less time in stages particularly vulnerable to attack.

Chiang (1968) shows how to calculate lifetime risks from age-classiﬁed

life tables. Here we compute these probabilities from stage-classiﬁed models

using the Markov chain description of the life cycle. We begin with the basic

structure (11.1.2) and add an additional absorbing state, “event-before-

death.” Because we are interested only in the probability of experiencing

the event, what happens to an individual after the event is irrelevant (of

course, it may be very relevant for other questions). Thus we can simply

leave individuals who have experienced the event in “event-before-death”

and not worry about them further.

Let α

be the probability that an individual in stage i experiences the

event in the interval (t, t + 1]. Carry out the following procedure.

1. Create a new matrix T



describing transitions of individuals that

neither die nor experience the event. Its entries are



=(1− α

) t

i, j ∈T. (11.2.1)

11.3. Age-Speciﬁc Traits From Stage-Speciﬁc Models 253

2. Create a new matrix M



containing the probabilities of transition

from each transient state to the two absorbing states



(1 − α

) m

i =1,j∈T

i =2,j∈T

(11.2.2)

The new transition matrix is







. (11.2.3)

3. Use the methods of Section 11.1.2.2 to compute the probability of

absorption in each of the two states.

B = M



(I − T



)

−1

. (11.2.4)

The lifetime event probability is the probability of absorption in

“event-before-death,” which is given by the second row of B.

11.3 Age-Speciﬁc Traits From Stage-Speciﬁc

Models

In a stage-classiﬁed model, the ages of individuals are not known, but it

is possible to calculate age-speciﬁc survivorship and fertility, mean age at

ﬁrst reproduction, net reproductive rate, generation time, and age-within-

stage distributions directly from the Markov chain describing the life cycle.

We will focus on two examples. One is the stage-structured model for

killer whales (Brault and Caswell 1993; see Example 11.1), because an

independent age-classiﬁed analysis exists for comparison (Olesiuk et al.

1990).

The second example is a stage-structured model for teasel (Dipsacus

sylvestris). Teasel is a weedy plant, introduced to North America from

Europe in the late nineteenth century. Seeds germinate to form ﬂattened

rosettes, which grow until they reach a critical size, at which point they

ﬂower and die. Seeds may remain dormant for up to a few years. A variety

of evidence pointed to size as the critical i-state variable, so Werner and

Caswell (1977, Caswell and Werner 1978) developed size-classiﬁed models

whose entries corresponded to the life cycle graph of Figure 11.2. Because

the projection interval was one year, reproduction in year t can produce

small, medium, or large rosettes in year t+1. The production of more than

one kind of oﬀspring is not common in human demographic models, but it

might appear in analyses of infant mortality or of family development; it is

not uncommon in ecological applications, and this example will show how

to account for it in calculations.

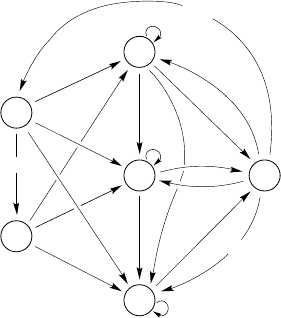
254 11. Markov Chains for Individual Life Histories

.013

30.170

.010

322.38

.966

.007

.008

Dormant

seeds

Rosettes

Flowering

.862

3.448

Dormant

seeds

Figure 11.2. A life cycle graph for teasel (Dipsacus sylvestris). Stages: N

ﬁrst-year dormant seeds, N

= second-year dormant seeds, N

= small rosettes,

= medium rosettes, N

= rosettes, and N

= ﬂowering plants.

Example 11.3 Markov chain decomposition for teasel

The population projection matrix for teasel is composed of transition

and fertility matrices

T =

⎛

⎜

⎝

000000

0.96600000

0.013 0.010 0.125 0 0 0

0.00700.125 0.23800

0.00800.038 0.245 0.167 0

0000.023 0.750 0

⎞

⎟

⎠

(11.3.1)

F =

⎛

⎜

⎝

00000322.388

00000 0

00000 3.448

00000 30.170

00000 0.862

00000 0

⎞

⎟

⎠

. (11.3.2)

ThesixthcolumnofT is zero because ﬂowering plants all die after

reproduction. The nonzero entries in the sixth column of F give the

production of diﬀerent kinds of oﬀspring (ﬁrst-year dormant seeds

and small, medium, and large rosettes). The resulting Markov chain