Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

11.3. Age-Speciﬁc Traits From Stage-Speciﬁc Models 255

transition matrix is

P =

⎛

⎜

⎝

000000

0.96600000

0.013 0.010 0.125 0 0 0

0.00700.125 0.238 0 0

0.00800.038 0.245 0.167 0

0000.023 0.750 0

0.006 0.990 0.712 0.494 0.083 1.000 1.000

⎞

⎟

⎠

11.3.1 Age-Speciﬁc Survival

Basic information on age-speciﬁc survival—the mean and variance of the

time spent in each stage, and the mean and variance of the time to

death—is obtained from the fundamental matrix N. For killer whales, the

fundamental matrix is

N =

⎛

⎜

⎝

1.00000

10.99 11.25 0 0

17.37 17.77 21.46 0

40.05 40.97 49.49 51.02

⎞

⎟

⎠

. (11.3.3)

Thus a yearling killer whale spends, on the average, about 11 years as an

immature, 17 years as a reproductive adult, and 40 years as a postreproduc-

tive female. A mature adult, in contrast, spends an average of 21 years in

that stage, and almost 50 years as a postreproductive. These averages are

larger than those for a yearling, because some yearlings spend zero years

as an adult or postreproductive, having died ﬁrst.

The variance in the amount of time spent in each stage, computed from

(11.1.14), is

V (ν

)

⎛

⎜

⎝

0000

115.5 115.300

426.4 429.1 439.00

2442.7 2461.1 2551.2 2552.1

⎞

⎟

⎠

. (11.3.4)

One way to interpret these variances is to compute the coeﬃcient of varia-

tion (the ratio of the standard deviation to the mean) of the time spent in

each stage, which is

CV (ν

)

⎛

⎜

⎝

0 −−−

0.98 0.95 −−

1.19 1.17 0.98 −

1.23 1.21 1.02 0.99

⎞

⎟

⎠

, (11.3.5)

where “−” denotes coeﬃcients of variation that are undeﬁned because both

the mean and the standard deviation are zero. There is considerable vari-

ation in the duration of each stage except the ﬁrst, with coeﬃcients of

variation on the order of 1.

256 11. Markov Chains for Individual Life Histories

The mean and variance of the time η

to death, given that the individual

starts in stage j are given by (11.1.15) and (11.1.17) with results

E (η

)

69.411 69.985 70.947 51.02

(11.3.6)

V (η

)

3341.4 3308.1 2990.3 2552.1

. (11.3.7)

The mean age at death is the life expectancy or expection of life; the life

expectancy of a newborn individual is 69.4 years, with a standard deviation

of 57.8 years. (You might want to add one year to this number to get the

average age at death, calculated from birth instead of from the yearling

stage.)

The mean age at death provides only part of the information about

survival. We can also calculate the age-speciﬁc survivorship (i.e., the prob-

ability of survival to age x) for individuals in each stage from the transition

matrix T, using (11.1.18).

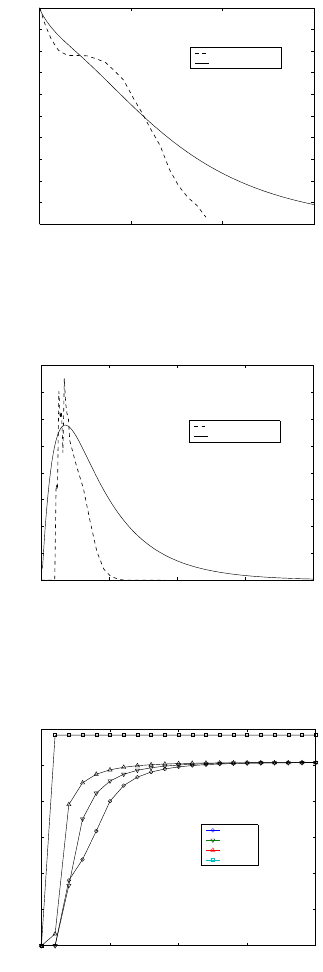
The survivorship conditional on starting in stage 1 (newborn) is shown

in Figure 11.3; this corresponds more or less

‡

to the classical survivorship

function l(x) starting at birth. The age-speciﬁc survivorship function re-

ported by Olesiuk et al. (1990) is shown for comparison. Survivorship from

the stage-classiﬁed model does not capture all the changes in age-speciﬁc

mortality. No surprise there; it is deﬁned by only four stage-speciﬁc sur-

vival probabilities. It does, however, capture the average survivorship from

birth up to 60 or 70 years of age. Survivorship of the oldest individuals is

much higher in the stage-classiﬁed model than in the age-classiﬁed model,

because the former ignores senescence of post-reproductive females.

11.3.2 Age-Speciﬁc Fertility

Age-speciﬁc fertility is described by a matrix Φ(x), whose entries φ

(x)

are the mean number of type i oﬀspring produced at age x by an individ-

ual starting in stage j at age 0. If stage j corresponds in any sense to a

“newborn” individual, then φ

(x) is the age-speciﬁc fertility in the usual

sense of the word.

The fertility matrix is calculated from T and F.The(i, j)entryofT

is the probability of being in stage i at time x, conditional on starting in

stage j. Dividing each column of T

by its sum gives the distribution of

individuals among stages at time x conditional on survival to time x:



diag (e

)



−1

. (11.3.8)

‡

Individuals in stage 1 (yearlings) do not correspond exactly to “newborn” individuals

in a life table, but more closely to an individual somewhere between 1/2 and 1 year old.

It is probably not worth trying to make the correspondence too exact.

11.3. Age-Speciﬁc Traits From Stage-Speciﬁc Models 257

Left-multiplying this matrix by the fertility matrix F gives the matrix of

fertilities at time x

Φ(x)=FT



diag (e

)



−1

. (11.3.9)

In the case of the killer whale, F contains only a single nonzero row, and

hence so does Φ(x). Thus at x = 1 the fertility is given by

Φ(1) = FT



diag



−1

(11.3.10)

⎛

⎜

⎝

0.0043 0.0124 0.1081 0

0000

⎞

⎟

⎠

. (11.3.11)

At x = 20, fertility has increased to

Φ(20) =

⎛

⎜

⎝

0.0573 0.0569 0.0503 0

0000

⎞

⎟

⎠

. (11.3.12)

The entry φ

(x) corresponds to the classical notion of age-speciﬁc fertility.

The other entries of the ﬁrst row give fertility at “age” x of an individual

starting life as an immature, mature, or postreproductive female, respec-

tively. Figure 11.4 shows φ

(x) as a function of age. An age-speciﬁc fertility

estimate is also shown.

The stage-classiﬁed model captures the overall

shape of the age-speciﬁc function, but produces some fertility earlier, and

a lot of fertility later, than does the age-classiﬁed analysis. This result is

to be expected, since the stage-classiﬁcation spreads out the passage of

individuals through the reproductive stage.

When there are multiple types of oﬀspring, there is no exact analogue

of age-speciﬁc fertility. Consider the case of teasel (Example 11.3) where

there are four types of oﬀspring. At x = 0, the fertility matrix is

Φ(0) =

⎛

⎜

⎝

00000322.38

00000 0

00000 3.45

00000 30.17

00000 0.86

00000 0

⎞

⎟

⎠

. (11.3.13)

Obtained by multiplying the m(x) ﬁgures in Table 14 of Olesiuk et al. (1990) by

their estimate (0.57) of survival to age 1/2.

258 11. Markov Chains for Individual Life Histories

This is just F, because only an individual in stage N

(ﬂowering plants)

can produce any oﬀspring at x =0.Atx = 3, we obtain

Φ(3) =

⎛

⎜

⎝

107.95 75.43 158.62 204.02 263.68 NaN

00000NaN

1.15 0.81 1.70 2.18 2.82 NaN

10.10 7.06 14.84 19.09 24.68 NaN

0.29 0.20 0.42 0.55 0.71 NaN

00000NaN

⎞

⎟

⎠

, (11.3.14)

where NaN (“not a number”) is the result of dividing 0 by 0 in Matlab.

Equation (11.3.9) will not work in this case, because the sixth column of

is always zero. Thus diag (e

) always has a zero in the (6, 6) position.

Although it is singular, Matlab will happily compute its inverse, but it

returns a matrix of NaNs, because the 0/0 division propagates throughout

the inversion process. A workable alternative is to compute the inverse

matrix as

diag(1./sum(Tˆx))

This produces a matrix Φ(x) with NaN entries only in the last column.

An individual that starts life as a dormant seed (N

) will, at age 3, pro-

duce an average of 108 dormant seeds, 1.15 small rosettes, 10.1 medium

rosettes, and 0.29 large rosettes, provided that it survives to age 3. These

multiple types of oﬀspring can be analyzed independently, or can be

summed to give total numbers of oﬀspring. Cochran and Ellner (1992)

suggested weighting the values by the reproductive value v calculated from

the stage-classiﬁed matrix A and then summing them.

The fact that an individual can be “born” in any of four diﬀerent stages

also complicates matters. At age x = 3 an individual born as a dormant

seed has less than half the reproductive output of an individual of the same

age that was born as a large rosette. Figure 11.5 shows the summed fertility,

as a function of age, for individuals born as dormant seeds and as small,

medium, and large rosettes. Fertility climbs and remains high indeﬁnitely

because this is the fertility of surviving individuals. Very few individuals

survivemorethanafewyears.

11.3.3 Age at First Reproduction

In an age-classiﬁed model, the age at ﬁrst reproduction is simply the ﬁrst

age x for which the maternity function m(x) is nonzero. It is not a good idea

to apply this approach to Φ(x) calculated from a stage-classiﬁed model. We

have just seen that the killer whale model predicts that some individuals

will reproduce at x = 1. A more reasonable measure would be the mean time

from birth (however that is deﬁned) to the ﬁrst entry into a reproductive

stage (Cochran and Ellner 1992). There may be several such stages, and

individuals may reach them at diﬀerent ages and by diﬀerent pathways. We

11.3. Age-Speciﬁc Traits From Stage-Speciﬁc Models 259

0 50 100 150

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Age (years)

Survivorship l(x)

Age−classified

Stage−classified

Figure 11.3. A comparison of the age-speciﬁc survivorship function for killer

whales derived from the stage-classiﬁed model of Brault and Caswell (1993) and

from the age-classiﬁed analysis of Olesiuk et al. (1990).

0 50 100 150 200

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

Age (years)

Age−specific fertility

Age−classified

Stage−classified

Figure 11.4. Age-speciﬁc fertility for killer whales calculated from the

stage-classiﬁed matrix model and from the age-speciﬁc maternity function m(x)

of Olesiuk et al. (1990).

0 5 10 15 20

100

150

200

250

300

Age (years)

Summed age−specific fertility

stage 1

stage 3

stage 4

stage 5

Figure 11.5. Age-speciﬁc fertility, summed over all oﬀspring types, for teasel

plants “born” in stages N

(dormant seeds), N

(small rosettes), N

(medium

rosettes), and N

(large rosettes).

260 11. Markov Chains for Individual Life Histories

want the mean, over all these pathways, calculated from individuals that

do not die ﬁrst, i.e., the mean conditional on reaching the reproductive

stage before death. This conditional mean is calculated by making the

set of reproductive stages absorbing, creating a new chain conditional on

absorption there, and calculating the mean time to absorption from that

chain.

1. Decide on a set of “reproductive” states; call this set R.

2. Create a new absorbing state, “reproduced-before-dying.”

3. Create a new transition matrix P



in which an individual that enters

any state in R spends one time step there and then is absorbed in

“reproduced-before-dying”:







, (11.3.15)

where



j/∈R

0 j ∈R

(11.3.16)



j/∈R

0 j ∈R

(11.3.17)



0 j/∈R

1 j ∈R

. (11.3.18)

We are interested only in the time required to reach R, not in what

happens afterward. Thus reproductive individuals can be left in the

“reproduced-before-dying” state after they reach R.

4. Calculate the probability of absorption in “reproduced-before-dying”

using (11.1.23),



= M



(I − T



)

−1

. (11.3.19)

The second row, b

2·

,ofB



gives the probabilities of reproducing

before death.

5. Create a new Markov chain conditional on absorption in “reproduced-

before-dying,” using (11.1.25) and (11.1.26):

(c)



(c)



, (11.3.20)

where

(c)

=diag(b



2·

) T



diag (b



2·

)

−1

. (11.3.21)

11.3. Age-Speciﬁc Traits From Stage-Speciﬁc Models 261

6. Generate the mean times to absorption for this conditional chain

using (11.1.15):



(c)



= e



I − T

(c)



−1

. (11.3.22)

For example, in the case of the killer whale model, R = {3} and the

transition matrix is [cf. (11.1.8]



⎛

⎜

⎝

0000

0.9775 0.9111 0 0

00.0736 0 0

0 000.9804

0.0225 0.0153 0 0.0196 10

0010

⎞

⎟

⎠

(11.3.23)

and





0.1907 0.1721 0 1.0000

0.8093 0.8279 1.0000 0



(11.3.24)

Thus, the probability of reaching maturity before death for an individual

starting in stage 1 is 0.8093. Notice that the probability of reproducing

before death is zero for an individual starting as a postreproductive female

(i.e., b



= 0). This means that the conditional transition probabilities for

stage 4 are undeﬁned (you cannot condition on an event of probability zero)

and that calculating

diag (b



2·

)

−1

involves 1/0.

This is not a major problem; it can be solved by inserting an arbitrary

nonzero value (we will use 1.0) for b



and then ignoring the conditional

probabilities for stage 4, since we know that individuals in stage 4 can never

reach stage 3. The resulting conditional transition matrix is

(c)

⎛

⎜

⎝

000−

1.00.9111 0 −

00.0889 0 −

000−

⎞

⎟

⎠

. (11.3.25)

The expected time to absorption in “reproduced-before-dying,” conditional

on eventual absorption in that state, is then



E(η

(c)

)



= e



I − T

(c)



−1

(11.3.26)

13.25 12.25 1.00 −

. (11.3.27)

262 11. Markov Chains for Individual Life Histories

The mean age at maturity is E



(c)



=13.25 years.

This agrees well

with Olesiuk et al.’s (1990) age-classiﬁed estimate of 13.1 years for the

mean age at ﬁrst birth.

11.3.4 Net Reproductive Rate

The net reproductive rate R

is the mean number of oﬀspring by which

a newborn individual will be replaced by the end of its life, and thus the

rate by which the population increases from one generation to the next.

Since the probability of surviving from birth to age x is l(x) and the rate

of reproduction at that age is m(x), this expectation is given by



∞

l(x)m(x) dx (11.3.28)

(Section 6.1).

The discrete equivalent, calculated from an age-classiﬁed matrix, is

= F

+ P

+ ··· (11.3.29)



i−1

j=1

. (11.3.30)

In age-classiﬁed models,

< 1 ⇔ λ

< 1

=1⇔ λ

= 1 (11.3.31)

> 1 ⇔ λ

> 1.

We would like a stage-classiﬁed net reproductive rate with all the proper-

ties of the age-classiﬁed rate; it should give the per-generation growth rate,

should relate to expected lifetime reproductive output, and should deter-

mine whether λ

is less than, equal to, or greater than one. This problem

has been attacked independently by Cushing (1988, 1997, Cushing and

Yicang 1994) and Cochran and Ellner (1992).

The fundamental matrix N gives the expected number of time steps

spent in each transient state, and the fertility matrix F gives the expected

number of oﬀspring of each type produced per time step. Thus the matrix

R = FN (11.3.32)

Some care is needed in translating between time to absorption and age at entering a

stage. We should subtract 1 from η

(c)

, because absorption in “reproduced-before-dying”

happens one time step after entering R. But then we should add 1, because absorption

is measured from stage 1, not from birth.

11.3. Age-Speciﬁc Traits From Stage-Speciﬁc Models 263

has entries r

that give the expected lifetime production



of type-i oﬀspring

of an individual starting life in stage j. In the case of the killer whale, the

matrix R is

R =

⎛

⎜

⎝

2.0131 2.0595 2.4292 0

0000

⎞

⎟

⎠

. (11.3.33)

A yearling female killer whale can expect to produce 2.01 female oﬀspring

during its life. Thus r

is an attractive candidate for R

, but the situation

is more complicated when there is more than one type of oﬀspring. For

teasel,

R =

⎛

⎜

⎝

3.66 0.27 27.33 103.06 290.26 322.39

000000

0.04 0.00 0.29 1.10 3.10 3.45

0.34 0.03 2.56 9.64 27.16 30.17

0.01 0.00 0.07 0.28 0.78 0.86

000000

⎞

⎟

⎠

. (11.3.34)

A plant starting life as a dormant seed (stage 1) can expect to produce

3.66 dormant seeds, 0.04 small rosettes, 0.34 medium rosettes, and 0.01

large rosettes over its lifetime. A plant starting life as a large rosette (stage

5), however, can expect to produce 290 dormant seeds, 3.1 small rosettes,

27.16 medium rosettes, and 0.78 large rosettes over its lifetime.

To account for multiple types of oﬀspring, consider the following calcu-

lation, inspired by Cushing and Yicang (1994). Let y(0) be a vector giving

the composition of an initial generation at t = 0. The fates of these in-

dividuals at t =1, 2,... are given by Ty(0), T

y(0), .... At each time,

the surviving individuals produce oﬀspring according to F ; thus, oﬀspring

production by this generation is Fy(0), FTy(0), FT

y(0), ....

Summing this oﬀspring production over the life of the generation gives

the next generation, y(1):

y(1) = Fy(0) + FTy(0) + FT

y(0) + ··· (11.3.35)

= F

I + T + T

+ ···

y(0) (11.3.36)

= F (I − T)

−1

y(0) (11.3.37)

= FNy(0) (11.3.38)

= Ry(0). (11.3.39)

Thus, R projects the population from one generation to the next. If R has

a dominant eigenvalue, that eigenvalue will give the rate of growth of the



Cushing and Yicang (1994) deﬁne R = NF, which does not give expected oﬀspring

production. However, as the eigenvalues of FN and of NF are the same, none of Cushing

and Yicang’s uses of R

are aﬀected.

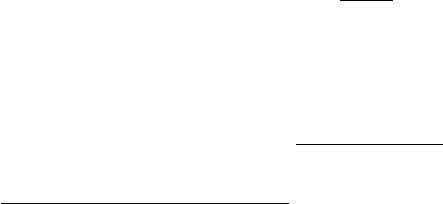
264 11. Markov Chains for Individual Life Histories

population from one generation to the next.

∗∗

Thus we conclude that

= dominant eigenvalue of R. (11.3.40)

When, as in the killer whale, there is only one type of oﬀspring, R has only

a single nonzero row, and the dominant eigenvalue is just r

We have shown that R

calculated as the dominant eigenvalue of R is

the per-generation growth rate. When there is only one oﬀspring type, it is

also the expected number of oﬀspring produced by an individual during its

lifetime. Cushing and Yicang (1994, Theorem 3) proved that R

calculated

from (11.3.40) also corresponds to λ as in (11.3.31).

11.3.5 Generation Time

There are several measures of generation time in age-classiﬁed models

(Coale 1972):

1. The time T required for the population to increase by a factor of R

which satisﬁes λ

= R

.Thus

T =

log R

log λ

; (11.3.41)

2. The mean age µ

of the parents of the oﬀspring produced by a cohort

over its lifetime. This is given by the mean of the net fertility schedule

l(x)m(x)



∞

xl(x)m(x) dx



∞

l(x)m(x) dx

, (11.3.42)

∗∗

Actually, this requires not only a dominant eigenvalue, but also convergence to the

corresponding eigenvector. In the case of the population projection matrix A, the strong

ergodic theorem guarantees this convergence. The alert reader may have noticed that

in Section 7.2 we assumed that A was similar to a diagonal matrix, and used that fact

in our proof of the ergodic theorem. A suﬃcient, but not necessary, condition for this

is that the eigenvalues be distinct, which they usually are for population projection

matrices. The eigenvalues of R, however, are usually not distinct; both the killer whale

and teasel examples have one positive eigenvalue and a repeated eigenvalue of zero.

The following result gives both necessary and suﬃcient condition for diagonalizability

(Horn and Johnson 1985, Corollary 3.3.8, p.145). Let the distinct eigenvalues of R be

,...,ρ

. The matrix R is diagonalizable if and only if

q(R)=(R − ρ

I)(R − ρ

I) ···(R − ρ

I)=0,

which is true for both the killer whale and teasel models. Even if R is not diagonalizable,

the Jordan canonical form can be used to show that the population will converge to the

dominant eigenvector.