Казаков К.А. Введение в теоретическую и квантовую механику

Подождите немного. Документ загружается.

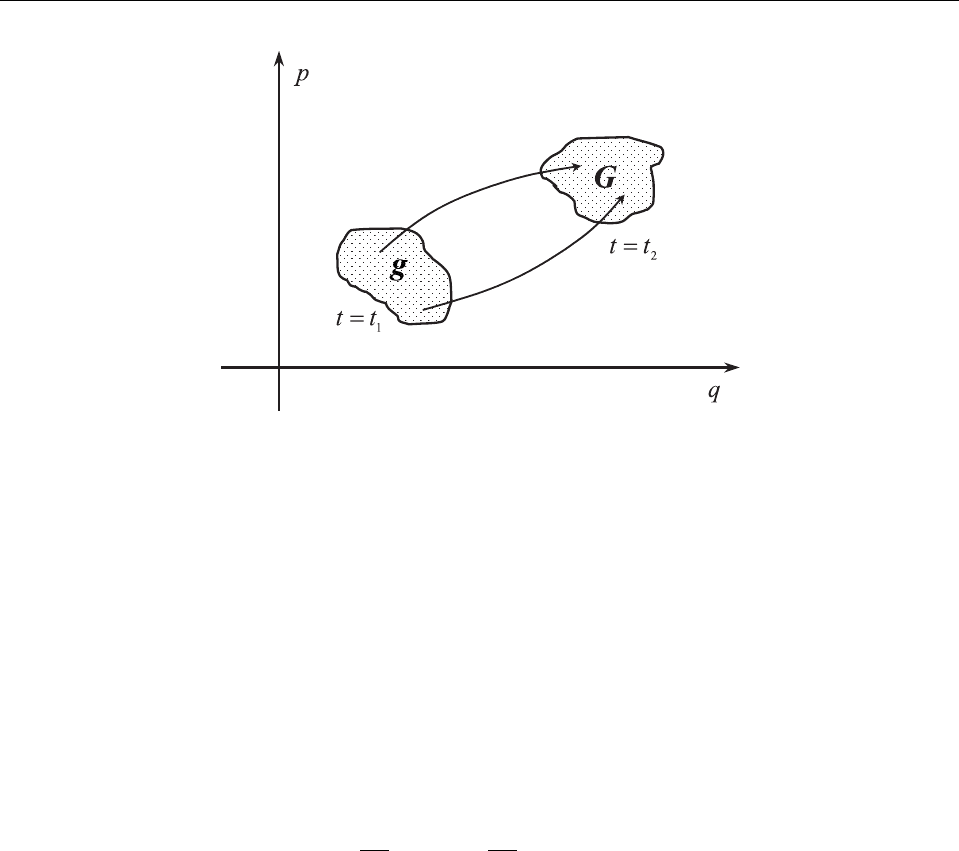
§5.5. Действие как функция координат и времени

Рис. 10: Эволюция области в фазовом пространстве в случае одномерной системы.

D. Уравнение Гамильтона-Якоби

Соотношения (5.60), (5.64) позволяют записать замкнутое уравнение для функции

S(q

(1)

, t

; q

(2)

, t

). Для этого зафиксируем момент времени t

и начальные координаты q

(1)

будем рассматривать зависимость действия лишь от параметров t

, q

(2)

, обозначая их для

краткости просто t, q. Соответственно, обозначение S(q

(1)

, t

; q

(2)

, t

) сократим до S(q, t).

Поскольку в дальнейшем все величины вычисляются на действителной траектории, чер-

та над q, p, H будет опускаться. Выражая аргументы p функции Гамильтона в правой

части (5.64) через производные от действия с помощью (5.60), приходим к уравнению

Гамильтона-Якоби

∂S

∂t

+ H

∂S

∂q

, t

= 0 . (5.68)

Уравнение (5.68) является нелинейным дифференциальным уравнением в частных произ-

водных первого порядка для действия S(q, t), являющегося функцией от s+1 независимых

переменных: s координат q

и времени t. Оказывается, что уравнение Гамильтона-Якоби

вполне эквивалентно уравнениям Гамильтона (или Лагранжа), в том смысле что решени-

ями этого уравнения определяется также и закон движения системы. Однако для этого

подходит далеко не всякое решение. Например, для свободной частицы уравнение (5.68)

имеет такое малоинтересное решение: S(q, t) = A с произвольной постоянной A. Выделим

нужный нам класс решений следующим определением: полным интегралом уравнения

Гамильтона-Якоби для системы с s степенями свободы называется его решение, содержа-

щее ровно s + 1 независимых произвольных постоянных интегрирования. Одной из этих

постоянных будет аддитивная постоянная, поскольку S входит в уравнение (5.68) только

через свои производные, так что если некоторое S(q, t) является его решением, то решени-

ем является и S

(q, t) = S(q, t)+A. Полный интеграл будем обозначать через S(q, C, t)+A,

где C = {C

}, α = 1, ..., s есть набор s независимых произвольных постоянных.

Покажем теперь каким образом можно найти закон движения системы, если известен

полный интеграл уравнения Гамильтона-Якоби. Для этого совершим каноническое преоб-

разование переменных q, p → Q, P, выбрав в качестве производящей функции Φ(q, P, t) =

Глава 5. Канонический формализм

S(q, P, t). Другими словами, функциональная зависимость действия от C

, α = 1, ..., s

рассматривается как зависимость от новых обобщенных импульсов P

, α = 1, ..., s. Та-

кое рассмотрение допустимо, т.к. постоянные C

по условию независимы и произвольны.

Тогда согласно формулам перехода (5.43) – (5.45) получим

∂S

∂q

, α = 1, ..., s , (5.69)

∂S

∂P

, α = 1, ..., s , (5.70)

= H +

∂S

∂t

. (5.71)

Но поскольку S удовлетворяет уравнению (5.68), то новая функция Гамильтона H

≡ 0.

Поэтому уравнения Гамильтона в новых переменных Q, P имеют следующий простой вид

= −

∂H

∂Q

= 0 , (5.72)

∂H

∂P

= 0 . (5.73)

Из уравнения (5.72) следует постоянство новых импульсов P

, α = 1, ..., s (эти постоянные

мы будем по-прежнему обозначать через C

), а из уравнения (5.73) – постоянство новых

координат Q

, α = 1, ..., s . Учитывая это обстоятельство, вернемся снова к уравнениям

(5.69) – (5.70). Первое из этих уравнений воспроизводит соотношение (5.60), определя-

ющее обобщенные импульсы в данной точке траектории по действию системы. Второе

же связывает обобщенные координаты системы и время, т.е. определяет закон движения

системы.

Итак, формулируем общий алгоритм решения основной задачи механики методом

Гамильтона-Якоби.

a. По функции Лагранжа системы построить ее функцию Гамильтона [см. §5.1].

b. С помощью найденной функции Гамильтона записать уравнение Гамильтона-Якоби

(5.68).

c. Найти решение этого уравнения S(q, C, t) + A, содержащее независимые произволь-

ные постоянные C (помимо аддитивной постоянной A) в числе, равном числу сте-

пеней свободы системы.

d. Продифференцировать найденную функцию S(q, C, t) по произвольным постоянным

C, приравнивая результаты дифференцирования новым произвольным постоянным

Q :

∂S(q, C, t)

∂C

= Q

α = 1, ..., s . (5.74)

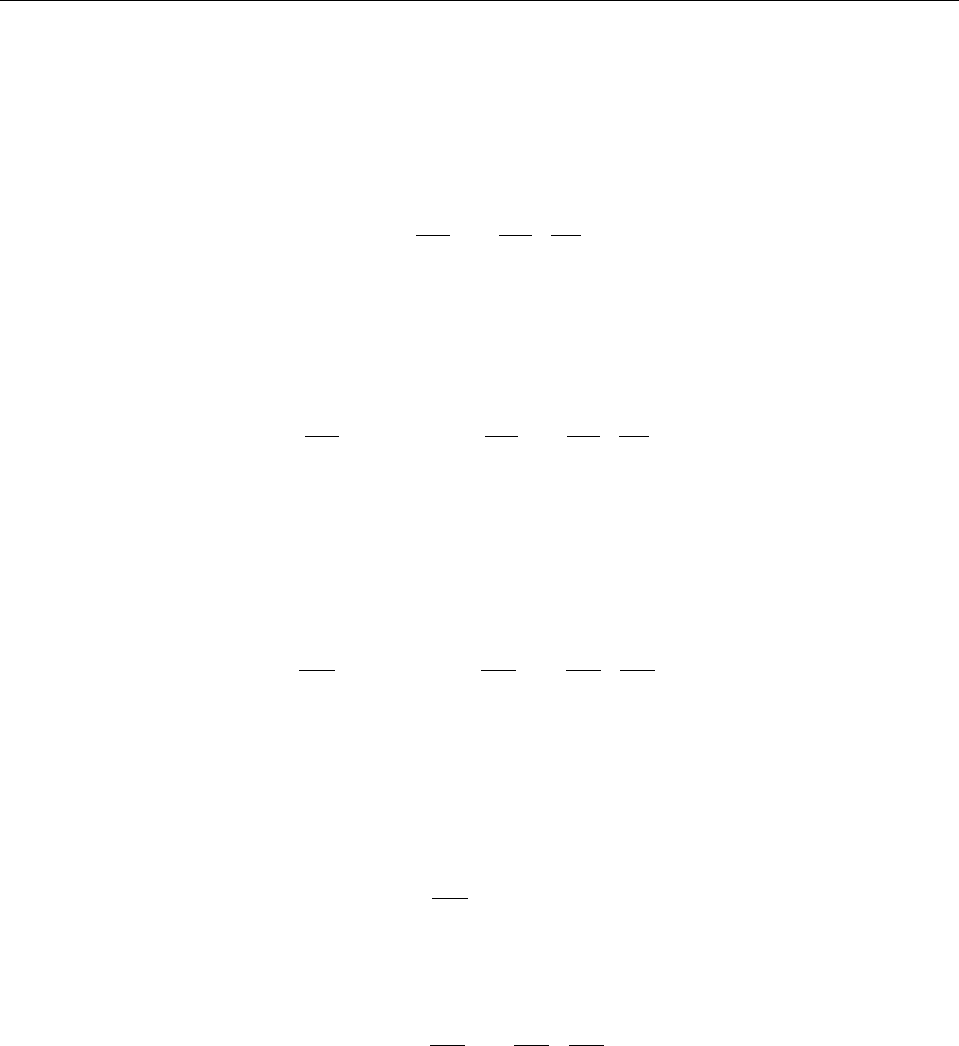
§5.5. Действие как функция координат и времени

E. Разделение переменных в уравнении Гамильтона-Якоби

Полный интеграл уравнения Гамильтона-Якоби может быть найден в квадратурах в

случае так называемых систем с разделяющимися переменными. Перепишем уравнение

(5.68) схематически в виде

, ..., q

, t,

∂S

∂q

, ...,

∂S

∂q

∂S

∂t

= 0 . (5.75)

Предположим, что какая-либо из независимых переменных, скажем q

, входит в это урав-

нение вместе с соответствующей производной ∂S/∂q

в некоторой комбинации, не содер-

жащей явно других переменных (неявно в S входят все переменные). Это означает, что

уравнение (5.75) имеет специальный вид

∂S

∂q

, q

, ..., q

, t,

∂S

∂q

, ...,

∂S

∂q

∂S

∂t

= 0 . (5.76)

В этом случае говорят, что переменная q

отделяется. Тогда решение уравнения

Гамильтона-Якоби можно искать в виде

S(q, t) = S

) + S

, ..., q

, t) . (5.77)

Подставляя это выражение в уравнение (5.76), получаем

, q

, ..., q

, t,

∂S

∂q

, ...,

∂S

∂q

∂S

∂t

= 0 . (5.78)

В результате в уравнении Гамильтона-Якоби выделилась комбинация f (q

, dS

/dq

) , ко-

торая ни явно, ни неявно не содержит переменные q

, ..., q

, t. Поскольку же все пере-

менные q

, ..., q

, t в уравнении Гамильтона-Якоби являются независимыми, то равенство

(5.78) может выполняться только в том случае, когда эта комбинация тождественно равна

некоторой постоянной:

= C

. (5.79)

Уравнение (5.79) является уже обыкновенным дифференциальным уравнением первого

порядка, которое может быть решено в квадратурах. Уравнение же (5.78) принимает вид

, q

, ..., q

, t,

∂S

∂q

, ...,

∂S

∂q

∂S

∂t

= 0 . (5.80)

Это уравнение имеет тот же вид, что и исходное уравнение (5.75), но содержит на одну

независимую переменную меньше. Может оказаться, что в уравнении (5.80) некоторая из

переменных q

, ..., q

, t снова отделяется. Тогда к ней следует применить описанную выше

процедуру. Если таким образом удается отделить все переменные, то в результате мы

получаем решение уравнения Гамильтона-Якоби в виде

S = A + S

(t) +

α=1

, C) , (5.81)

содержащее s + 1 независимых произвольных постоянных A, C

, α = 1, ..., s, т.е. полный

интеграл.

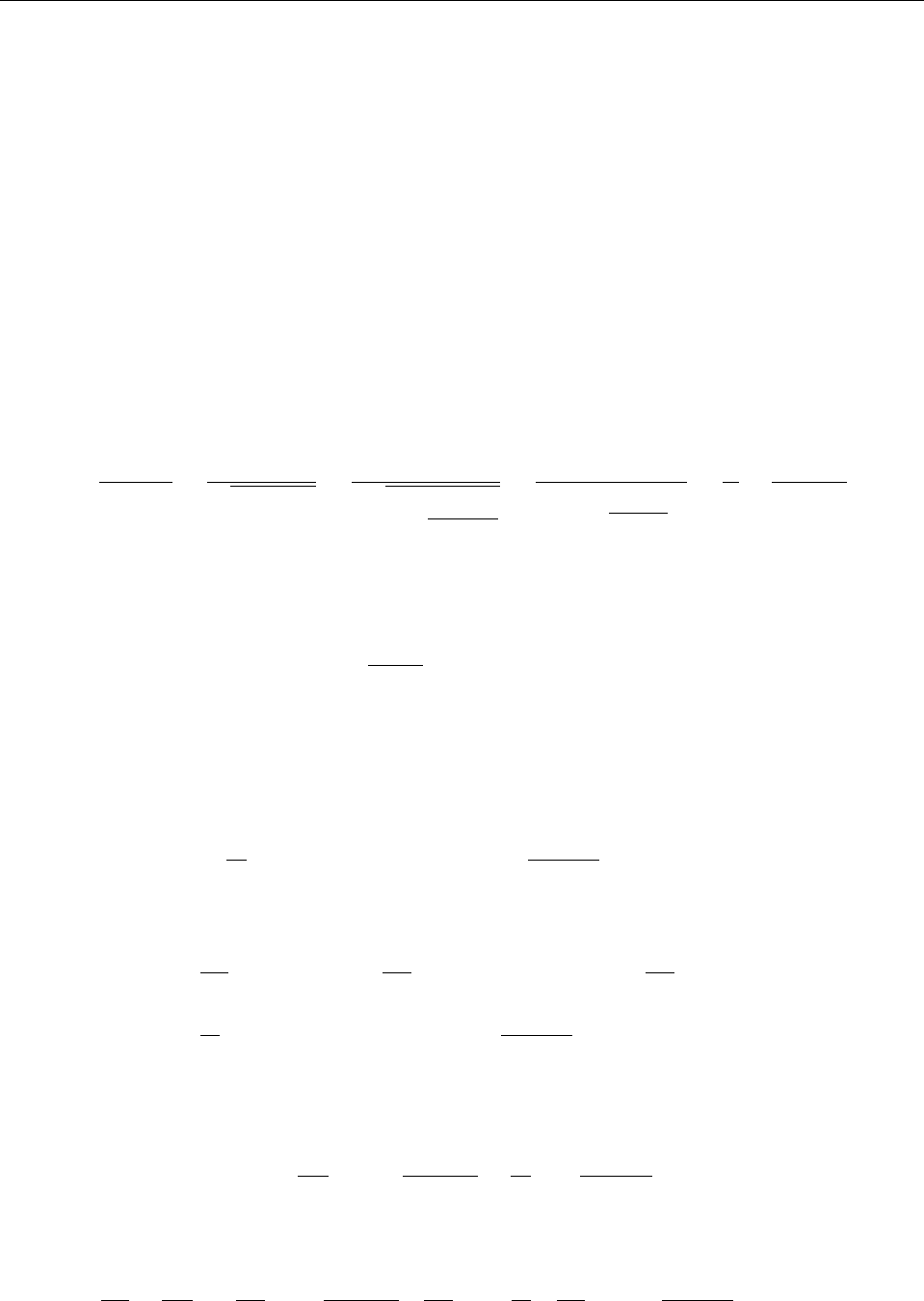
Глава 5. Канонический формализм

Пример 22. Движение в поле электрического диполя. Рассмотрим заряженную материаль-

ную точку, движущуюся в поле системы зарядов на расстояниях, больших по сравнению

с характерными размерами системы. Даже если система является в целом электрически

нейтральной, на точку будет действовать некоторая сила благодаря тому, что кулоновы

поля частиц, составляющих систему, не вполне компенсируют друг друга. Например, при

движении электрона в поле молекулы H Cl электрон будет притягиваться к молекуле,

облетая ее со стороны атома водорода, и отталкиваться со стороны атома хлора. Опре-

делим потенциал поля такой системы. Выберем начало декартовой системы координат

где-нибудь внутри системы и обозначим через r

, i = 1, ..., n радиус-векторы составляю-

щих ее частиц, а через r – радиус-вектор материальной точки. По условию,

|r| À |r

|, i = 1, ..., n .

Используя это неравенство, кулонов потенциал i-ой частицы в точке r можно прибли-

женно написать как (q

– ее заряд)

|r − r

(r − r

)

≈

1 −

2(r, r

)

≈

1 −

(r, r

)

≈

(r, r

)

Суммируя по всем частицам и учитывая электронейтральность системы (

i=1

= 0), по-

лучаем

ϕ =

(d, r)

, d =

i=1

Вектор d называется дипольным моментом системы. Найдем закон движения точки в

случае, когда d не зависит от времени. Выберем сферическую систему координат с нача-

лом в точке r = 0 и полярной осью, направленной параллельно вектору d. Тогда функция

Лагранжа материальной точки будет иметь вид

L =

˙r

+ r

sin

+ r

−

qd cos θ

, d ≡ |d| (5.82)

(q – ее заряд). Отсюда находим обобщенные импульсы и обобщенную энергию точки

∂L

∂ ˙r

= m ˙r , p

∂L

∂

= mr

sin

φ , p

∂L

∂

= mr

θ , (5.83)

E =

˙r

+ r

sin

+ r

qd cos θ

Выражая обобщенные скорости через обобщенные импульсы и подставляя результат в

обобщенную энергию, находим функцию Гамильтона

H =

sin

qd cos θ

Наконец, по функции Гамильтона записываем уравнение Гамильтона-Якоби

∂S

∂t

(

∂S

∂r

sin

∂S

∂φ

∂S

∂θ

)

qd cos θ

= 0 . (5.84)

§5.5. Действие как функция координат и времени

Переменные t, φ входят в это уравнение лишь через производные ∂S/∂t, ∂S/∂φ. В соот-

ветствии с методом разделения переменных ищем решение в виде

S = S

(t) + S

(φ) + S

(r, θ)

и приходим к уравнениям

= C

dφ

= C

(

∂S

∂r

sin

∂S

∂θ

)

qd cos θ

= 0 .

Первые два из этих уравнений интегрируются тривиально:

= C

t , S

= C

φ .

Перепишем последнее уравнение в виде

2mC

∂S

∂r

sin

∂S

∂θ

+ 2mqd cos θ

= 0 .

Из этой записи видно, что переменная θ отделяется, поэтому мы полагаем

= S

(θ) + S

(r)

и получаем уравнения

sin

dθ

+ 2mqd cos θ = C

2mC

= 0 .

Их решения имеют вид

− 2 mqd cos θ −

sin

dθ ,

−2mC

−

dr .

Итак, мы нашли решение уравнения Гамильтона-Якоби в виде

S = A + C

t + C

φ +

− 2mqd cos θ −

sin

dθ +

−2mC

−

dr . (5.85)

Это решение содержит произвольные постоянные A, C

, C

, θ

, r

. Однако изменение

, r

эквивалентно переопределению A, так что независимыми являются лишь посто-

янные A, C

, C

. Их число равно числу степеней свободы материальной точки плюс

Глава 6. Канонический формализм

один, следовательно, выражение (5.85) представляет собой полный интеграл уравнения

(5.84). Определим знаки, с которыми следует брать корни в этом решении. Подставляя

его в соотношения (5.69), находим значения обобщенных импульсов p

, p

в данной точке

траектории:

= ±

−2mC

−

, p

= ±

− 2mqd cos θ −

sin

С другой стороны, согласно формулам (5.83) знаки этих импульсов совпадают со знаками

соответствующих обобщенных скоростей. Таким образом, подынтегральное выражение в

интеграле по r в формуле (5.85) следует брать с верхним (нижним) знаком, если на данном

участке траектории ˙r > 0 ( ˙r < 0), и аналогично для интеграла по θ.

Выясним теперь физический смысл постоянных C

, C

. Подставляя решение (5.85)

в уравнение Гамильтона-Якоби находим C

+ H(q, p, t) = 0 , т.е. постоянная C

есть ве-

личина обобщенной энергии точки, взятая со знаком минус. Подстановка же решения в

соотношения (5.69) дает p

= ∂S/∂φ = C

. Таким образом, постоянная C

есть величина

сохраняющейся проекции момента импульса точки на направление вектора d.

То, что величины E, p

в рассматриваемой задаче сохраняются, можно было утвер-

ждать заранее, поскольку время в ней однородно, а пространство изотропно относитель-

но поворотов системы (материальной точки) вокруг направления d [функция Лагран-

жа (5.82) не зависит от переменных t, φ явно]. Сохранение же комбинации (C

/ sin

θ +

+ 2mqd cos θ) никак не связано с подобными симметриями и является специфическим

для данной задачи. В том, что метод Гамильтона-Якоби позволяет регулярным образом

находить такие интегралы движения, заключается его существенное преимущество по

сравнению с лагранжевым методом.

Наконец, найдем закон движения материальной точки. Дифференцируя решение (5.85)

по постоянным C

≡ −E, C

≡ M

, C

и приравнивая результат новым произвольным

постоянным, получаем

−t +

mdr

2mE −

= Q

, (5.86)

φ −

dθ

±sin

− 2 mqd cos θ −

sin

= Q

, (5.87)

dθ

− 2mqd cos θ −

sin

−

±r

2mE −

= Q

. (5.88)

Уравнение (5.86) определяет в неявном виде зависимость r(t), а уравнения (5.87), (5.88) –

зависимости φ(θ) и θ(r). Таким образом, мы нашли решение уравнений движения мате-

риальной точки в квадратурах. Оно содержит 6 независимых произвольных постоянных

E, M

, C

, Q

, которые могут быть определены из начальных условий.

§6.1. Уравнение Гамильтона-Якоби как предел уравнения Шредингера

Глава 6. ПЕРЕХОД ОТ КЛАССИЧЕСКОЙ К КВАНТОВОЙ МЕХАНИ-

КЕ

Основным уравнением квантовой механики является уравнение Шредингера для так

называемой волновой функции системы. Если рассматриваемая система является класси-

ческой, т.е. ее движение может быть с достаточной точностью описано с помощью урав-

нений классической механики (например, солнечная система), то уравнение Шредингера

для такой системы должно каким-то образом сводиться к уравнениям классической ме-

ханики. Оказывается, что классическим пределом уравнения Шредингера является урав-

нение Гамильтона-Якоби. Поэтому в качестве первого шага перехода от классической

механики к квантовой мы формально “восстановим” уравнение Шредингера из уравне-

ния Гамильтона-Якоби. Важнейшим отличием в структуре этих уравнений является то,

что уравнение Шредингера является линейным. Затем мы обсудим связь этого изменения

в структуре основного уравнения с теми изменениями в основных положениях механики,

которые требуется сделать при переходе к описанию явлений микромира.

§6.1. Уравнение Гамильтона-Якоби как классический предел уравнения Шре-

дингера

Преобразуем уравнение Гамильтона-Якоби (5.68), введя вместо S(q, t) новую неизвест-

ную функцию Ψ(q, t) с помощью соотношения

Ψ(q, t) = exp

S(q, t)

, (6.1)

где i есть мнимая единица, а ~ = 1, 055 · 10

−27

г·см

/с есть так называемая постоянная

Планка. В силу малости этой постоянной для обычных классических систем, которые мы

рассматривали до сих пор, всегда выполняется условие

S À ~ . (6.2)

Ограничимся для простоты случаем одномерного движения материальной точки массы m

в потенциальном поле U(x, t). Здесь x обозначает декартову координату точки. Уравнение

Гамильтона-Якоби в этом случае имеет вид

∂S

∂t

∂S

∂x

+ U(x, t ) = 0 . (6.3)

Дифференцируя соотношение (6.1) один раз по времени и дважды по координатам, по-

лучаем

∂Ψ

∂t

∂S

∂t

exp

∂S

∂t

Ψ , (6.4)

∂

∂x

∂

∂x

∂S

∂x

exp

¾¸

= −

∂S

∂x

exp

∂

∂x

exp

−

∂S

∂x

∂

∂x

Ψ .

Глава 6. Переход от классической механики к квантовой

В силу условия (6.2) второй член в квадратных скобках в последнем выражении мал по

сравнению с первым. Поэтому можно приближенно написать

∂

∂x

= −

∂S

∂x

Ψ . (6.5)

Домножая уравнение (6.3) на Ψ, переписываем его с помощью соотношений (6.4), (6.5) в

следующем виде

∂Ψ

∂t

= −

∂

∂x

+ U (x, t)Ψ , (6.6)

Это уравнение называется уравнением Шредингера и является основным уравнением

квантовой механики. Несмотря на то, что мы получили его приближенно из уравнения

Гамильтона-Якоби, именно уравнение (6.6) оказывается точным, т.е. описывающим любые

системы, а не только те, что удовлетворяют условию (6.2). Таким образом, проделанный

выше “вывод” уравнения Шредингера следует рассматривать как демонстрацию того, что

уравнение Гамильтона-Якоби является классическим пределом уравнения Шредингера.

Заметим для дальнейшего, что правую часть уравнения (6.6) можно представить как

ˆp

+ U(x)

Ψ ,

где

ˆp = −i~

∂

∂x

есть так называемый оператор импульса, причем квадрат оператора понимается как его

повторное применение два раза. При этом выражение в круглых скобках имеет вид функ-

ции Гамильтона частицы в данном поле, в которой импульс частицы заменен его опе-

ратором. Поэтому ˆp

/2m + U(x) называется оператором энергии, или гамильтонианом

частицы. Значение операторов в квантовой механике будет объяснено в следующей главе,

а сейчас заметим лишь, что действие оператора импульса на функцию (6.1) сводится к

умножению этой функции на текущий импульс частицы. Действительно, согласно фор-

муле (5.69) имеем

ˆpΨ(x, t) = −i~

∂

∂x

exp

S(x, t)

∂S

∂x

exp

S(x, t)

= p(x, t)Ψ(x, t) .

Важнейшим качественным отличием уравнения Шредингера от уравнения

Гамильтона-Якоби является его линейность: если две функции Ψ

(x, t) Ψ

(x, t)

удовлетворяют уравнению (6.6), то ему удовлетворяет и любая их линейная комбинация

(x, t) + c

(x, t), где c

, c

– произвольные постоянные.

§6.2. Основные предположения квантовой теории

В этом параграфе мы определим те изменения в основных положениях механики, кото-

рые требуется сделать при переходе от классического к квантовому описанию природы.

По той же причине, по которой уравнение Шредингера нельзя вывести из уравнений

§6.2. Основные предположения квантовой теории

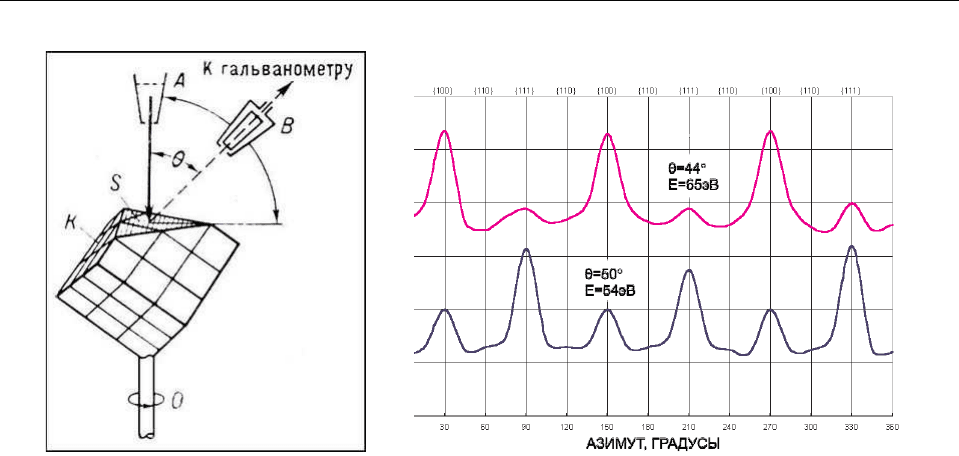
Рис. 11: Слева: схема опыта Дэвиссона — Джермера: K — монокристалл никеля; A — источник

электронов; B — детектор электронов; θ — угол отклонения электронных пучков; пучок электро-

нов падает перпендикулярно отшлифованной плоскости кристалла S. При поворотах кристалла

вокруг оси O гальванометр, присоединенный к датчику B, дает периодически возникающие мак-

симумы. Справа: графики зависимости тока (в условных единицах) детектора от угла поворота

вокруг оси O для различных значений угла θ и энергии электронов E.

классической механики, новые положения можно лишь угадать, опираясь на данные экс-

перимента. Исторически, это “угадывание” происходило в первой четверти XX века.

Первое, от чего следует отказаться при переходе к квантовому описанию, это понятие

закона движения (в частности, траектории) частицы как зависимости ее координат от вре-

мени вида {q

(t)}. Как показывают наблюдения, это основное для классической механики

понятие несовместимо с поведением объектов микромира. Об этом говорят, например, ре-

зультаты опыта Дэвиссона-Джермера по рассеянию электронов на кристаллах (он был

поставлен американскими физиками К. Дэвиссоном и Л. Джермером в 1927 г. уже после

создания квантовой механики). В этом опыте пучок медленных электронов в вакууме на-

правлялся на монокристалл никеля (см. Рис. 11). Регистрация рассеянных электронов по-

казала, что они образовывали интерференционные картины, характерные для рассеяния

на кристаллах рентгеновских лучей. Максимумы и минимумы интенсивности в обоих слу-

чаях возникают в результате взаимного усиления или ослабления вторичных волн, порож-

даемых атомами кристалла при прохождении через него пучка электронов или фотонов.

Таким образом, движение элементарных частиц имеет волновой характер, означающий, в

частности, отсутствие определенного положения у каждой частицы, в противоположность

корпускулярному движению классической механики – движению материальных точек по

определенным траекториям. Математически, эта “размазанность” электрона выражает-

ся в том, что положение электрона в квантовой механике должно описываться не тремя

параметрами (обобщенными координатами), имеющими в каждый момент времени опре-

деленные значения, а некоторой функцией пространственных координат. Эта функция

называется волновой функцией. Она определяет, таким образом, степень “размазанности”

частицы в пространстве. Например, для того чтобы в опыте Дэвиссона-Джермера наблю-

далась интерференционная картина, эта размазанность (т.е. область, в которой волновая

Глава 6. Переход от классической механики к квантовой

функция отлична от нуля) должна быть больше периода кристаллической решетки, так

чтобы электрон рассеивался одновременно на нескольких атомах. Напротив, в областях,

в которых электрон находиться не может, она должна быть равна нулю. Поскольку ин-

терференционные картины, наблюдающиеся в опытах по рассеянию электронных и элек-

тромагнитных волн, очень похожи друг на друга, а электромагнитные поля удовлетво-

ряют линейным уравнениям Максвелла, то естественно предположить, что линейность

является свойством также и уравнений квантовой механики. Таким образом, мы делаем

следующее

Предположение 1: Уравнение для волновой функции должно быть линейным.

С другой стороны, мы видели выше (на простейшем примере одномерного движения),

что уравнения классической механики могут быть приближенно представлены в линейном

виде. А именно, как было указано в конце предыдущего параграфа, уравнение Шредин-

гера (6.6), “полученное” из уравнения Гамильтона-Якоби при ~ → 0, является линейным.

Поэтому естественно сделать

Предположение 2: уравнение (6.6) является в действительности точным, и его сле-

дует принять в качестве основного уравнения квантовой механики, отождествив функцию

Ψ(x, t) с волновой функцией.

Сами по себе эти предположения пока еще не отменяют классических понятий закона

движения и траектории, поскольку переход по формуле (6.1) от функции S(x, t) к Ψ(x, t)

представляет собой не более, чем замену неизвестной функции. Закон движения и уравне-

ния траектории в классической механике определяются решением уравнения Гамильтона-

Якоби по правилу (5.74). Напомним, что в самом уравнении Гамильтона-Якоби перемен-

ные x, t являются независимыми, и только после подстановки его решения в уравнения

(5.74) возникает зависимость x(t), т.е. закон движения. Поэтому отказ от этого понятия

означает отмену уравнений (5.74). Таким образом, мы делаем

Предположение 3: Эволюция системы в квантовой механике определяется полно-

стью одним лишь уравнением Шредингера. При этом аргументы x, t волновой функции

остаются полностью независимыми.

Предположения 1 – 3 в корне меняют понятие состояния системы (см. §1.1). А именно,

поскольку уравнение Шредингера является дифференциальным уравнением первого по-

рядка по времени, то для однозначного его решения, т.е. определения эволюции системы,

следует задать лишь начальное значение функции Ψ(x, t) в некоторый момент време-

ни t = t

, тогда как в классическом случае требовалось задать дополнительно значения

постоянных Q

в уравнениях (5.74). Но и этого изменения понятия состояния еще недоста-

точно для того, чтобы получить принципиально новую механику. Если мы отказываемся

от знания части начальных условий в форме набора постоянных Q

, ограничиваясь за-

данием Ψ(x, t

), то это означает лишь изменение способа наблюдения за системой, а не

физических свойств самой системы. Действительно, этот отказ вносит в описание систе-

мы неопределенность, аналогичную неопределенности термодинамического описания, при

котором наблюдатель отказывается от знания всей совокупности данных о координатах

и скоростях отдельных частиц системы, заменяя ее гораздо меньшим числом параметров

(температура, давление, концентрации отдельных компонент и их химические потенциа-

лы и т.д.). Рассмотрим, например, атом водорода. Даже если наблюдатель отказался от

попытки точно измерить значения параметров Q

, задающих закон движения электрона,

эти параметры в действительности имеют какие-то определенные значения, т.е. электрон

движется по определенной траектории. Но согласно электродинамике любое ускоренное

движение заряда приводит к излучению им электромагнитных волн. Эти волны непре-