Казаков К.А. Введение в теоретическую и квантовую механику

Подождите немного. Документ загружается.

§4.3. Движение твердого тела

Рис. 9: Возникновение приливного бугра на Земле под влиянием гравитационного поля Луны.

Угловая скорость вращения Земли Ω

⊕

больше угловой орбитальной скорости Луны ω, поэтому

бугор смещается от линии Земля-Луна в направлении вращения Земли.

Пример 14. Влияние приливных сил на движение системы Земля-Луна. Если бы силы тя-

готения между планетами были строго центральными (зависящими лишь от положения

их центров масс), приближение, в котором планеты рассматриваются как материальные

точки, было бы точным. Однако в действительности имеются отклонения от центрально-

сти, связанные с тем, что распределения масс в планетах не являются строго сферически-

симметричными. Одной из причин этой несимметричности являются сами силы тяготения

между планетами, приводящие к тому, что взаимодействующие планеты слегка вытяги-

ваются в направлении, соединяющем их центры. Примером такого рода влияния Луны

на Землю являются морские приливы. Из-за того, что скорость вращения Земли больше

угловой орбитальной скорости Луны, приливный бугор несколько смещается от направле-

ния Земля-Луна в направлении вращения Земли, поскольку массам воды для перемеще-

ния требуется некоторое время. Получающаяся конфигурация показана схематически на

Рис. 9. Сила тяготения Луны, действующая на приливный бугор, стремится вернуть его

на линию Земля-Луна. Возникающая своеобразная “сила трения,” называемая приливной

силой, тормозит вращение Земли. Однако поскольку сила тяготения является потенци-

альной, это трение не приводит к уменьшению полной механической энергии или полного

момента импульса системы. Исходя только лишь из этих законов можно ответить на ин-

тересный вопрос о том, как будет двигаться система, когда приливные силы полностью

затормозят относительное вращение Земли и Луны, т.е. когда угловые скорости их вра-

щения сравняются. Сделаем это, предполагая для простоты, что орбиты тел являются

круговыми, а оси их вращения перпендикулярны плоскости орбиты. Для этого запишем

выражение сохраняющегося момента импульса системы. Он складывается из момента

импульса орбитального движения тел и момента импульса их вращения. Орбитальный

момент импульса находим по формуле (3.16) задачи двух тел:

orb

= mr

ω , (4.64)

где m обозначает приведенную массу системы

m =

⊕

+ m

а ω – угловая скорость вращения вектора r = r

−r

⊕

; нижние индексы ⊕, L относятся к

Земле и Луне, соответственно. По условию задачи моменты импульса вращения Земли и

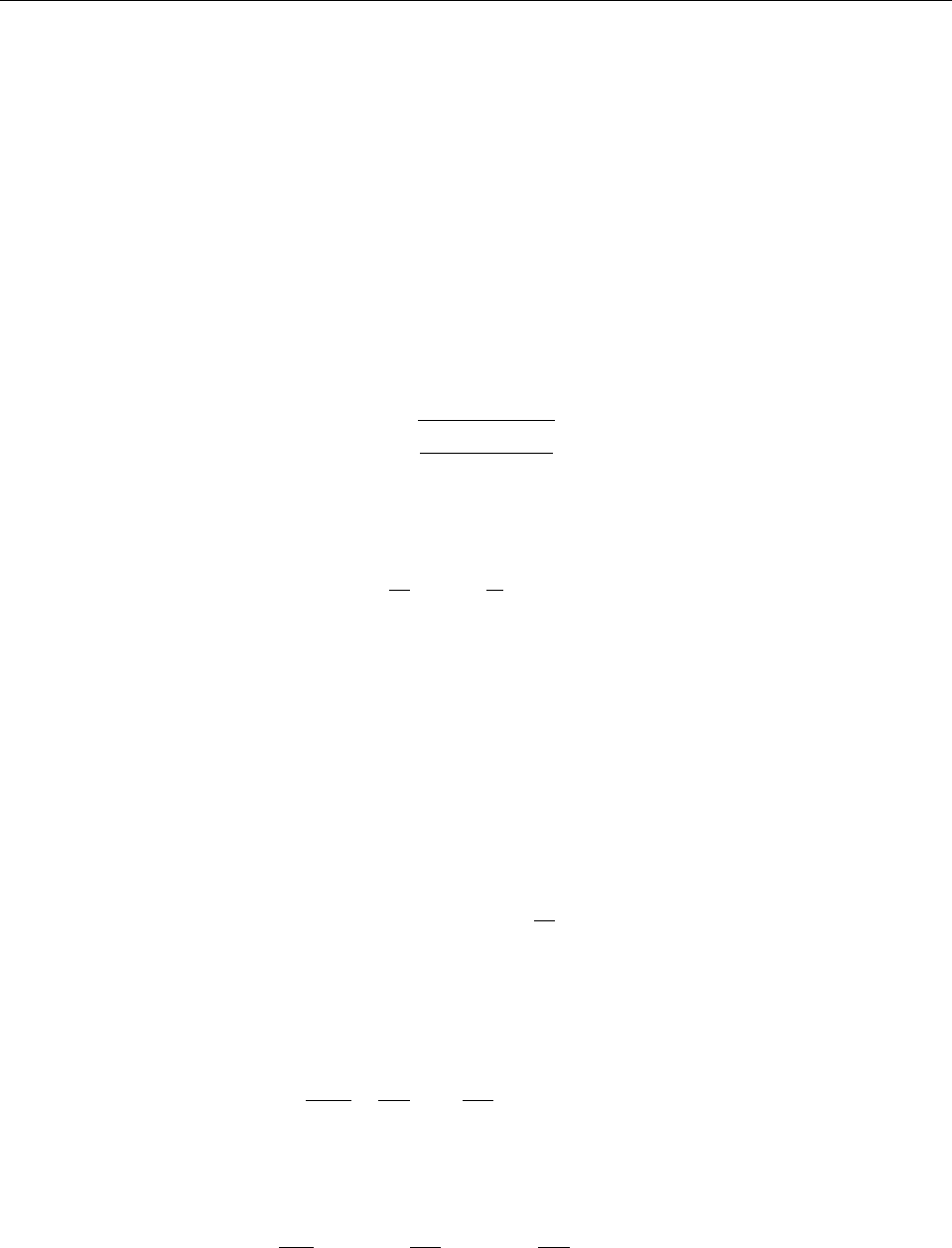
Глава 5. Интегрирование уравнений движения

Луны перпендикулярны плоскости орбиты и, согласно формуле (4.40), по величине равны

⊕

= I

⊕

Ω

⊕

, M

= I

Ω

. (4.65)

При вычислении моментов инерции Земли и Луны их можно считать шаровыми волч-

ками, поскольку изменение распределения массы планеты под действием приливных сил

относительно мал´o. Таким образом, полный момент импульса системы равен

M = mr

ω + I

⊕

Ω

⊕

+ I

Ω

= const . (4.66)

С другой стороны, поскольку изменение орбит под действием приливных сил происходит

очень медленно, движение системы на каждом витке хорошо описывается решением за-

дачи двух тел, полученным в §3.3. Подставляя T = 2π/ω, a = r, |α| = Gm

⊕

в формулу

(3.38), получаем

ω =

G(m

⊕

+ m

)

откуда следует, что текущие значения параметров ω, r связаны с их конечными значени-

ями ω

, r

соотношением, аналогичным третьему закону Кеплера

. (4.67)

Учитывая, что в конечном состоянии

= Ω

⊕

находим из уравнения (4.66)

ω + I

⊕

Ω

⊕

+ I

Ω

= ω

+ I

⊕

+ I

Подставляя сюда r

из уравнения (4.67), получаем уравнение для конечной угловой ско-

рости

ω + I

⊕

Ω

⊕

+ I

Ω

= ω

4/3

+ I

⊕

+ I

. (4.68)

Используя формулу (4.45) и учитывая, что масса Луны примерно в восемьдесят раз мень-

ше массы Земли, а ее радиус – почти в четыре раза меньше земного, пренебреаем I

по

сравнению с I

⊕

, полагаем m ≈ m

и переписываем уравнение (4.68) в виде

1 +

⊕

Ω

⊕

− x

= x

−1/3

, (4.69)

где x = ω

/ω, причем нас интересуют решения x < 1 (т.к. приливные силы замедляют

вращение). Текущие значения параметров, входящих в это уравнения, таковы:

⊕

= 81 ,

Ω

⊕

= 27 ,

⊕

= 1/60 .

При этих значениях решением уравнения (4.69) является x ≈ 0, 53, т.е. продолжитель-

ность земных суток составит 1месяц/0, 53 ≈ 27 · 24 часа/0, 53 ≈ 1220 часов. При этом

= rx

−2/3

≈ 1, 53r.

§5.1. Уравнения Гамильтона

Глава 5. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ

§5.1. Уравнения Гамильтона

Основной величиной, определяющей механические свойства систем в формализме

Лагранжа, является функция Лагранжа L(q, ˙q, t). В рамках самой классической механики

эта функция не имеет непосредственного физического смысла. Для решения ряда задач

классической механики, а также при формулировке перехода к квантовой теории удобно

работать с величинами, более тесно связанными с механическими свойствами систем. Ока-

зывается, что уравнения движения механики можно представить в виде, в котором роль

основной величины, определяющей механические свойства системы, играет обобщенная

энергия системы, а в качестве независимых переменных используются обобщенные коор-

динаты и обобщенные импульсы системы. Математически такой переход осуществляется

с помощью так называемого преобразования Лежандра, которое состоит в следующем.

Построим полный дифференциал функции Лагранжа

dL(q, ˙q, t) =

α=1

∂L

∂q

α=1

∂L

∂ ˙q

d ˙q

∂L

∂t

dt . (5.1)

Величина ∂L/∂ ˙q

есть, по определению, обобщенный импульс p

, соответствующий обоб-

щенной координате q

. Для краткости, обозначение p

будет сокращаться ниже до p

С этим обозначением, а также с помощью уравнений Лагранжа равенство (5.1) можно

переписать так:

dL(q, ˙q, t) =

α=1

˙p

α=1

d ˙q

∂L

∂t

dt . (5.2)

Правая часть уравнения (5.2) содержит дифференциалы независимых переменных q, ˙q и

t. Для того чтобы перейти от этого набора к новому набору независимых переменных

q, p, t, напишем тождественно

d ˙q

= d(p

˙q

) − ˙q

, α = 1, ..., s

и представим уравнение (5.2) в виде

α=1

˙q

− L (q, ˙q, t)

= −

α=1

˙p

α=1

˙q

−

∂L

∂t

dt . (5.3)

Тот факт, что правая часть этого тождества содержит дифференциалы переменных q, p, t

означает, что величина, стоящая в его левой части под знаком полного дифференциала,

также может быть выражена как функция этого набора переменных. В соответствии с

определением (2.13), эта величина численно совпадает с обобщенной энергией системы.

Выраженная через обобщенные координаты и импульсы (и время), она называется функ-

цией Гамильтона системы и обозначается через H(q, p, t). Таким образом, по определе-

нию, при построении функции Гамильтона переменные q, p рассматриваются как незави-

симые переменные, аналогично тому, как в функции Лагранжа независимыми являются

переменные q, ˙q. Для того чтобы получить эту функцию, следует разрешить определение

Глава 5. Канонический формализм

p = ∂L/∂ ˙q относительно ˙q и подставить результат в функцию E(q, ˙q, t):

H(q, p, t) =

α=1

˙q

− L(q, ˙q, t)

˙q= ˙q(p,q)

Расписав явно полный дифференциал функции H(q, p, t) в левой части (5.3), получим

α=1

∂H

∂q

α=1

∂H

∂p

∂H

∂t

dt = −

α=1

˙p

α=1

˙q

−

∂L

∂t

dt . (5.4)

Приравнивая коэффициенты при дифференциалах независимых переменных в этом тож-

дестве, находим следующие уравнения

˙p

= −

∂H

∂q

, α = 1, ..., s , (5.5)

˙q

∂H

∂p

, α = 1, ..., s , (5.6)

∂H

∂t

= −

∂L

∂t

. (5.7)

Уравнения (5.5), (5.6) представляют собой систему 2s дифференциальных уравнений пер-

вого порядка для 2s функций q

(t), p

(t), α = 1, ..., s, которые заменяют s уравнений вто-

рого порядка (1.16) лагранжева формализма. Эти уравнения называются уравнениями

Гамильтона или каноническими уравнениями.

A. Интегрирование уравнений Гамильтона

Для нахождения закона движения системы необходимо проинтегрировать дифферен-

циальные уравнения (5.5), (5.6). Так же как и в формализме Лагранжа, для этого надо

сначала исследовать систему на наличие законов сохранения. Если пространство одно-

родно или изотропно по каким-либо направлениям, следует выписать соответствующие

законы сохранения (2.5), (2.8), выразив левые их части через обобщенные координаты и

обобщенные импульсы. В таком виде они будут представлять интегралы уравнений Га-

мильтона. В случае однородности задачи по времени следует записать закон сохранения

обобщенной энергии (2.13). Как мы знаем, признаком сохранения обобщенной энергии яв-

ляется равенство нулю частной производной ∂L/∂t. Из уравнения (5.7) следует, что при

этом и ∂H/∂t = 0. Таким образом, если функция Гамильтона системы не зависит явно от

времени, то имеет место закон сохранения

H(q, p) = const .

Найденные законы сохранения следует дополнить уравнениями из набора (5.5), (5.6) так,

чтобы в результате получить 2s независимых уравнений для 2s функций q

(t), p

(t), α =

1, ..., s и проинтегрировать полученную систему уравнений.

§5.1. Уравнения Гамильтона

Пример 15. Функция Гамильтона гармонического осциллятора. Функция Лагранжа гар-

монического осциллятора

L(x, ˙x) =

m ˙x

−

mω

где m, ω – масса и частота осциллятора. Из выражения для обобщенного импульса осцил-

лятора

p =

∂L

∂ ˙x

= m ˙x

находим обобщенную скорость

˙x =

Подставляя это выражение в обобщенную энергию осциллятора

E =

m ˙x

mω

находим его функцию Гамильтона

H(x, p) =

mω

. (5.8)

Пример 16. Функция Гамильтона заряженной частицы в электромагнитном поле. Из функ-

ции Лагранжа (1.22) находим обобщенный декартов импульс частицы в электромагнит-

ном поле

p =

∂L

∂

= m

r +

A(r, t) .

Отсюда

r =

p −

A(r, t)

. (5.9)

Подставляя это выражение в обобщенную энергию (2.17), получаем функцию Гамильтона

H(r, p, t) =

p −

A(r, t)

+ qϕ(r, t) .

Пример 17. Гармонический осциллятор с частотой, зависящей от амплитуды. Рассмотрим

одномерную систему, функция Гамильтона которой имеет вид

H(x, p) =

mω

+ λ

mω

, (5.10)

где m, ω, λ – постоянные положительные параметры. Найдем закон движения системы.

Поскольку функция Гамильтона (5.10) не зависит от времени явно, то имеем закон со-

хранения

mω

+ λ

mω

= const ,

откуда следует, что

mω

= C , (5.11)

Глава 5. Канонический формализм

с некоторой положительной постоянной C. Это уравнение связывает две неизвестных

функции x(t), p(t). Дополним его уравнением (5.6):

˙x =

∂H(x, p)

∂p

+ 2λ

mω

Выражая здесь p через x с помощью (5.11), получаем дифференциальное уравнение для

функции x(t) :

˙x = ±(1 + 2λC)

− ω

интегрируя которое путем разделения переменных, находим

x(t) =

mω

sin {(1 + 2λC)ω(t − t

)} .

Этот закон описывает гармоническое колебание с частотой Ω = (1 + 2λC)ω и амплитудой

A =

2C/mω

. Другими словами, частота рассматриваемых колебаний зависит от их

амплитуды согласно

Ω = ω(1 + λmω

) .

B. Скобки Пуассона

Уравнения Гамильтона можно представить в формально симметричном виде, если вве-

сти так называемую скобку Пуассона, определенную для двух функций обобщенных ко-

ординат и обобщенных импульсов f(q, p), g(q, p) (эти функции также могут зависеть от

времени или от каких-либо других параметров):

{f, g} =

α=1

∂f

∂p

∂g

∂q

−

∂f

∂q

∂g

∂p

. (5.12)

Тогда уравнения (5.5) и (5.6) могут быть переписаны в виде

˙p

= {H, p

}, α = 1, ..., s , (5.13)

˙q

= {H, q

}, α = 1, ..., s . (5.14)

Действительно, учитывая независимость переменных q, p, имеем, например,

{H, p

} =

β=1

∂H

∂p

∂q

−

∂H

∂q

∂p

= −

β=1

∂H

∂q

αβ

= −

∂H

∂q

Заметим, что с помощью скобок Пуассона можно компактно записать выражение для

полной производной по времени от произвольной функции f(q, p, t), а именно, используя

уравнения Гамильтона, получаем

α=1

∂f

∂q

˙q

∂f

∂p

˙p

∂f

∂t

α=1

∂f

∂q

∂H

∂p

−

∂f

∂p

∂H

∂p

∂f

∂t

§5.1. Уравнения Гамильтона

или

= {H , f} +

∂f

∂t

. (5.15)

Оказывается, что значение операции, определенной в (5.12), простирается гораздо даль-

ше простых соображений удобства. Скобки Пуассона обладают рядом важных свойств,

для вывода которых приведем сначала несколько простых правил их вычисления, непо-

средственно следующих из определения. Для любых функций f, g, h, зависящих от обоб-

щенных координат и импульсов, а также, возможно, от некоторого параметра λ (роль

которого может играть, например, время t)

{f, g} = −{g, f}, (5.16)

{f + h, g} = {f, g} + {h, g}, (5.17)

{fh, g} = h{f, g} + f{h, g}, (5.18)

∂

∂λ

{f, g} =

∂f

∂λ

, g

∂g

∂λ

. (5.19)

Докажем, например, свойство (5.18). Имеем

{fh, g} =

α=1

∂(fh)

∂p

∂g

∂q

−

∂(fh)

∂q

∂g

∂p

α=1

∂f

∂p

∂g

∂q

+ f

∂h

∂p

∂g

∂q

− h

∂f

∂q

∂g

∂p

− f

∂h

∂q

∂g

∂p

= h

α=1

∂f

∂p

∂g

∂q

−

∂f

∂q

∂g

∂p

+ f

α=1

∂h

∂p

∂g

∂q

−

∂h

∂q

∂g

∂p

= h{f, g} + f {h, g}.

Докажем теперь следующее важное и нетривиальное свойство скобок Пуассона: для лю-

бых трех функций f, g, h справедливо тождество Якоби

{f, {g, h}} + {g, {h, f }} + {h, {f, g}} = 0 . (5.20)

Это тождество проверяется прямым вычислением. Левая его часть представляет со-

бой сумму членов, каждый из которых пропорционален второй производной одной из

функций f, g, h по переменным q, p. В силу симметрии относительно перестановки этих

функций, достаточно доказать, что каждая из производных ∂

f/∂p

∂p

, ∂

f/∂q

∂q

∂

f/∂q

∂p

входит в левую часть (5.20) с нулевым коэффициентом. Проверим это, напри-

мер, для вторых производных ∂

f/∂p

∂p

. Отмечая члены, не содержащие производных

Глава 5. Канонический формализм

∂

f/∂p

∂p

, многоточием, имеем

{f, {g, h}} = 0 + ··· ,

{g, {h, f}} =

(

g, −

α=1

∂h

∂q

∂f

∂p

)

+ ··· = −

β=1

∂g

∂q

∂

∂p

−

α=1

∂h

∂q

∂f

∂p

+ ···

α,β=1

∂g

∂q

∂h

∂q

∂

∂p

+ ··· ,

{h, {f, g}} =

(

α=1

∂f

∂p

∂g

∂q

)

+ ··· = −

β=1

∂h

∂q

∂

∂p

α=1

∂f

∂p

∂g

∂q

+ ···

= −

α,β=1

∂h

∂q

∂

∂p

∂g

∂q

+ ··· = −

α,β=1

∂h

∂q

∂

∂p

∂g

∂q

+ ··· .

Складывая эти выражения и учитывая перестановочность вторых производных, мы ви-

дим, что члены, содержащие производные ∂

f/∂p

∂p

, действительно сокращаются.

Теперь с помощью тождества Якоби мы докажем следующее интересное утверждение,

называемое теоремой Пуассона: Если две функции f(q, p, t) и g(q, p, t) являются интегра-

лами движения, т.е.

f = ˙g = 0, то интегралом движения является и их скобка Пуассона

{f, g}. Доказательство. Поскольку по условию теоремы f и g остаются постоянными при

движении системы, то из формулы (5.15) следует, что

∂f

∂t

= −{H , f},

∂g

∂t

= −{H , g}. (5.21)

Вычислим полную производную по времени от {f, g} по формуле (5.15):

d{f, g}

= {H , {f, g}} +

∂{f, g}

∂t

Применяя правило (5.19) дифференцирования скобки Пуассона по параметру и учитывая

уравнения (5.21), получаем

d{f, g}

= {H, {f, g}} − {{H, f}, g} − {f, {H, g}},

или, переставляя аргументы скобок Пуассона по правилу (5.16),

d{f, g}

= {H , {f, g}} + {g, {H, f}} + {f, {g, H}}.

Правая часть последнего равенства равна нулю в силу тождества Якоби. Теорема дока-

зана.

C. Вычисление скобок Пуассона

Практически наиболее удобно вычислять скобки Пуассона, последовательно упрощая

их с помощью правил (5.16) – (5.18). Если хотя бы один из аргументов данной скобки

§5.1. Уравнения Гамильтона

Пуассона является полиномом по обобщенным координатам и обобщенным импульсам,

то в результате такого упрощения приходят к скобкам Пуассона вида {q

, f} или {p

, f}.

Из определения (5.12) следует, что

, f} = −

∂f

∂p

, {p

, f} =

∂f

∂q

. (5.22)

В частности,

, q

} = δ

αβ

, {q

, q

} = 0 , {p

, p

} = 0 . (5.23)

Скобки (5.23) называют фундаментальными скобками Пуассона.

Пример 18. Скобки Пуассона компонент момента импульса. Найдем скобки Пуассона x, y-

компонент момента импульса частицы, предполагая, что обобщенными координатами яв-

ляются декартовы компоненты ее радиус-вектора. Имеем

, M

} = {(yp

− zp

), (zp

− xp

)}

= {yp

, zp

} − {zp

, zp

} − {yp

, xp

} + {zp

, xp

}

= y{p

, z}p

+ p

{z, p

}x . (5.24)

Для краткости, в последней строке здесь выписаны лишь члены, содержащие ненулевые

фундаментальные скобки Пуассона. Подставляя сюда {p

, z} = −{z, p

} = 1, находим

, M

} = yp

− p

x = −M

Аналогично можно получить формулы

, M

} = −M

, {M

, M

} = −M

Из этих формул и теоремы Пуассона следует, что если проекции момента импульса на

какие-либо две декартовы оси (инерциальной) системы отсчета сохраняются, то сохраня-

ется также и его проекция на третью ось.

Пример 19. Скобки Пуассона компонент скорости частицы в электромагнитном поле. Рас-

смотрим, далее, заряженную частицу в электромагнитном поле и вычислим скобки Пуас-

сона компонент вектора ее скорости v, например, {v

, v

}. Для этого необходимо сначала

выразить компоненты вектора v через обобщенные координаты и обобщенные импуль-

сы частицы с помощью формулы (5.9). Выписывая опять лишь нетривиальные скобки

Пуассона, получаем

, v

} =

−

(r, t)

−

(r, t)

= −

[{A

(r, t), p

} + {p

, A

(r, t)}]

∂A

(r, t)

∂y

−

∂A

(r, t)

∂x

, (5.25)

или, используя обозначение (1.25),

, v

} = −

Глава 5. Канонический формализм

§5.2. Принцип наименьшего действия

Аналогично тому, как уравнения Лагранжа могут быть получены из принципа мини-

мальности действия (2.19), так и уравнения Гамильтона могут быть получены из условия

минимальности следующего функционала действия

S[q(t), p(t)] =

α=1

˙q

− H(q, p, t)

dt , (5.26)

в котором по-прежнему предполагаются фиксированными значения обобщенных коорди-

нат в начальный и конечный моменты времени:

) = q

(1)

, q

) = q

(2)

, α = 1, ..., s . (5.27)

причем при отыскании минимума действия S[q(t), p(t)] функции p(t) варьируются неза-

висимо от функций q(t), что и отражено добавлением p(t) вторым аргументом в обозна-

чение функционала действия.

Вывод уравнений Гамильтона из принципа наименьшего действия вполне аналоги-

чен выводу уравнений Лагранжа, подробно разобранному в §2.3. Пусть функционал

S[q(t), p(t)] принимает наименьшее значение на функциях ¯q(t), ¯p(t), где ¯q(t) удовлетво-

ряют условиям (5.27). Рассмотрим виртуальную траекторию, описываемую функциями

¯q(t) + δq(t), ¯p(t), где малые функции δq(t) удовлетворяют условиям

δq

) = δq

) = 0 , α = 1, ..., s . (5.28)

При этом действие получает приращение

δS = S[¯q(t) + δq(t), ¯p(t)] − S[¯q(t), ¯p(t)] =





α=1

¯p

δ ( ˙q

) −

α=1

∂H(q, ¯p, t)

∂q

q=¯q

δq





dt .

Используя равенство (2.1) и интегрируя по частям, находим

δS =

α=1

¯p

δq

−

α=1

¯p

∂H(q, ¯p, t)

∂q

q=¯q

δq

dt . (5.29)

Поскольку правая часть этого уравнения линейна по вариации δq(t), необходимым усло-

вием минимума действия является δS = 0. Первый член в правой части (5.29) равен нулю

в силу условий (5.28), интегральный же член может быть равен нулю, только если равны

нулю множители при всех независимых произвольных вариациях δq

, α = 1, ..., s :

¯p

∂H(q, ¯p, t)

∂q

q=¯q

= 0 , α = 1, ..., s .

Таким образом, функции ¯q(t), ¯p(t) должны удовлетворять s уравнениям Гамильтона (5.5).