Капутин Ю.Е., Ежов А.И., Хейнли С. Геостатистика в горно-геологической практике
Подождите немного. Документ загружается.


в
кuчестве
примера
со
з
дадим
условн
у
ю
м
д
е
Л
l>
одного
из
алмазных
месторождени
1.
Для
расчета
в
з
нт
.
часть
тру
б
ки
с
р
е
дним
диаметром
200
м
между
отметками
-20
и
+280
м
.
Исходная
блочная
модель
ОСТОIIТ
из
о
д
инаковых
блоков
размерами
20х20х50
м
(послеДliе~
юмеР~lIне
-
высота
блока).
Количество
блоков
в
модели
- 854.
.
Интерполянин
пока
:
штелл
содержании
а.llМП
:
ЮВ
D
руде
провощшась
методом
линеiillОГО
КРl1гинга
с
ИСПО
J
IЬЗОIi
i.
НiИСМ
данных
кернового
опробованю/
месторождеНЮI
.
Сред
нее
(условно
е
)
сод
е
ржание
в
пробах
-
8.52,
диспер
с
и
я
-
61
.9.
ДЛSl
Pi1C'j~T
O
U
примеЮlIН\
С Ь
.
I1
з
отр
о
пн
а
я
одноструктурная
сферическ:
:
ш
МОДсJII,
8i\p110l
'
paMMb!
с
п
а
рuм~трами
:
Со =
30,
С
1 =30,
А
=
60
м.
Вначале
с
помощью
npOfpi.lMMbI
КRGЗDА
рассчитывались
Кр'игинговы~
OIleltKl1
Д
Л
Я
каждого
блока
модели.
Затем,
с
помощью
программы
СО
N S 1
М
про
в
однтю
с
ь
УСЛ
ОВ
ll
ое
МОДСЛИРОН:11-lИе
.
Бьша
ИСfЮJlЬЗОШIlШ
Ti1
ж
е
ваРIЮГРi1ММ/I
Ш
I
мод
е
т
.
,
нормали
з
аЦИJl
ИСХОДНЫХ
данных
J1Р060ди
л
ас[,
с
помuщыо
ПOJIИНОМ08
рми
т
а,
а
обуславливани
е
ЗН:lLJеllllЙ
модели
D
ТО4ках
опробоваНIНI
-
с
помощью
KO-КРlIгинга.
Результаты
расче
т
ов
приведены
в
таблице
6.1.
т
б
61
С
а
л
.
_
р
1
шнеНllе
реЗУ
Л1,т
а
то
в
крНГИIIГII
и
УСJlОВНОГО
модеJlирова
нил
Метод
расчета
С[)сднее
сuдержание
Дисперсия
8
блоках
модели
tщеttеllНЫХ
блокorl
КРЮ
·
ИlIГ
6
.
зоз
10
.
129
-
УСЛОК/lОС
6.32
79.
13
модешtроваllие
-._--
--
И
з
т
а
блиц
I
ВИДIIО,
ч
т о
у с
л
о
шю~
м
о
д
еЛ
IlР
О
В
i.1
l1l1
е
д
а
ет
д
а
же
ДJ
НI
неБОJII
.
ulOГО
и оч
е
нь
с
лаб
о
оп
р о б о
ванного
у'(астка
м~
с
торождеНIIЛ
ДIiСll
е
р
с
ню
блюкую
к
р
е
а
л ьной
(
ДJШ
пр
о б
Щ
:
ТaJll>lюii
ра
з
в
е
дки).
Эта
ДИСIl
С
РСШl o'leHI. L
I1
J1
bHO
ОТЛl1'Н\
еТ
н
ог
диспtр
С
ИI1
СГЛ:.l
же
нных
оц
е
llОК
криг
и
нга
.
Опр
е
д
еле
нный
отп
е
ча
т
ок на
р
езул
ьт
аты
Д
i1I1
Н
ОГО
IlРI-Iм
е
р
а
ока
ЗaJ
Ш
очень
р
~
дкая
сеть
опроБОD::ННUI
данно
г
о
учас
т
ка
мес
т
орожд
е
ния.
6.2.
П"имеры
"раю
ическо
г
о
IJримеllенин
УСJ
I
ОИllOfО
моделирования
flри
наl1и~ании
данн
о
о
ра здел
а
в
ос
н
о
в
юм
нсп
о
ль
з
OlШНЫ
материалы
главы
7
монографии
141
.
Рассма
риваемый
пр
е
дмет
пока
н
е
ПОПУJlнр
е
н
8
Оценке
за
rШСО8,
и
потому
не
располагает
большим
количе
ст
вом
м
ет
одов
и
КОМПI)ю
'
·е
рных
програмr.l.
Один
из
немногих
из
tJестных
пак
ст
ов
прогр
.
мм
для
у
словно
го
мод
е
лировани
я
POLVSIM2
н
а
lll1сан
на
Форгр
а
l1
е
к
омпанией
Geo
s
tnt
Sy
te
1l1
s
Illt
ДJШ
2
-
х
MepHoI'O
МО
ДС
J1ированиs.
В
пр
ог
р
а
мму
вво
д
я
т
ся
координаты
Х,у
то'/ск
опробов
а
ния
и
измерн
е
мая
в
Л
И'IИН:.I.
;
Мод
е
лиру
е
мы
е
прогр
а
ММ
О
I1
2
-
х
Mt
pHbl
e
ДШll1ы
е
I1М~ЮТ
те
же
ста
ИСТI1Ч
С
Сl<ие
хар
а
к
т
еРИСТII
и/
г
истог
ра
мму
,
НЩНЮI
'
р
а
мм
у
11
T.
II
./ ,
как
н
peaJlbHMe
даllllые
.
Во
вс
е
х
СЛУЧ
i1
Н
Х с
()
дство
м
е
жд
у
p~ёlJ
lbl
i
bIM~1
Ilрu
б
:ШII
и
М
О
~
JlИр
уе
МЫМИ
Н
<1
'l
е
ншш
и
об
е
~
1
'/lша
е
l
СН И
С
l
lOJ
l
l>зуемо
й
мО)
~
еЛhlО
l
Э
О

вuриограммы
.
Это
и
будет
"оБУСЛОВJlивание.м"
моделируемы.х
зн
.
ачениЙ
реальными
ДiiННЫМИ
.
Моделнруемые
зваченин
р"змещаются
в
точках
реГУШlРНОЙ
нро
ст
ранственн()й
сети
или
в
заранее
зада
нных
ПРОИЗDОJlЬНЫХ
тuчках.
В
нuстонщ
е е
вреМII
пакет
может
рnботать
с
3
-){
мерными
моделнми
и
включает
5
прогр
амм.
Первые
дnе:
TGAUSS
и
VARJOJ
служат
для
статистических
В
ЫЧl1
слениli
110
ре
а
л
ь
н
ым
дан
ным
опробования:
первая
-
приводит
фпктичс
сх
е
рn
с
преде)(енис
к
нормальному,
а
вторая
рассчитывает
Э
J<спеРllмеllТnЛ
ЬН
IС
вuр и
ограммы.
Другие
3 I1POl'PU
MM
t.(
обсспе
~
I
И
D
ают
моделирование.
SJMUL2 -
это
основ
ная
про
грамма
.J.J.JlЯ
получения
н
ормалИЗО8анных
данных
с
YLiCTOM
указанной
D<ЧJI10граммы~
SfMUL2C,
а
fTGAUSS-
н,осстанавливает
т
ребуемую
гисто
гр
ММУ
да
н
ных.
В
каждой
ИЗ
этих
программ
может
быть
в
ыполн
е
н
подробный
ста
истический
анализ
моделируемых
данных
и
проверка
их
соотнст
с
тnи
п
реальным
проба
м
.
6.2. J.
Пример
ИСПШIЬЗОВ
..
Я
naKe
га
для
медноii
ЖИЛЫ
.
Ни
же
Jlр
и
ве
де
н
прнмер
2-
х
мер
ного
модели
рования
со
де
ржания
меди
в
неРТIIК~UIЬНОЙ
Жl1flе,
разме
рами
550*400
м,
опробованной
77
полными
пересеtl~НИНМИ
по
нерегулярной
сети
.
Ср
еднее
расстояние
между
про
бами
-
30
м
.
Моделрование
выполнено
по
регулярной
сети
15*15
м
.
Поскольку
моделируемые
зна'lения
должны
иметь
Т4.1кие
же
распр
деление
и
В[\
РИО
ГР[\~
I
МУ
как и для
исходного
множества
проб
,
то
8
наЧШl
е
лроводитсн
стат
и
стически
й
анализ
данных
с
помощью
программ
TGAtJSS
1I
VЛRtоз
.
После
tlНaJ1I1Эr1
р
::!с
пр
еделен
ия
реальных
да
нных
п
ервая
ПРОl'р
а
мма
о
пре
деляет
фун
кцию
Y=f
Х),
с
помощью
которой
исходное
раСl1ред
сление
щ.ю
б
У
п
реобр
а
з
уетсн в
но
р
мальное
Х
с
о
среДн
им
=0
и
дис
п
ерсией
= 1.
Распред
еле
ние
ИСХОДНЫХ
данных
имеет
характе
ри
стики:
-ч
и
сло
Прuб
. -
77
;
-
средн
ее
-
1.42
-медиа
l1а
- 1.4)
-ста
ндuртн
\~
.
отклонение
- 0.277
-ми
н
имум
-
0.8
-м,
ксимум
- 2.34
Можн
OTMeTI1Tb
очеllЬ
маленькое
различие
между
средним
И
медианой
,
а
также ШU1ич
ие
D
массиве
данн
ых
од
но
й
пр()бы
с
"ураганнЬ1М"
з
н
ачением
2.
34.
Для
при
вед
е
ния д
а
нного
рас
пр
еде
л
ен
ия
к
ИОР
М
:
U1ьному
lIро
граммой
тqлuss
lIол
уttен:\
фунКl
ин
,
и
спользую
щ
а
я
полином
ы
Эр
мит
а
с
коэффици
е
н
тами:
CTeJleHb
Ко
'
ффи
ц
нент
О
1.4
1 0.277
'2
0.000698
J 0.0076')
4
-
а
.
ОО
49
1:11

ТеоретИ~Jеское
стандартное
отклонеЮ1е
раl:l
НО
0.279.
Как
и
требовалось,
число
членов
в
разложении
-
,однако
ДJlЯ
практического
использования
можно
оставить
2,
Т
.
е
.
ур.
внение
функции
име
,
ет
вид
у=
1.4+0.277Х.
что
подтверждает
,
близость
и
сходного
раСl1ределенИJf
к
нормальному
.
Нпчальные данные
(У)
бшlИ
нормали
зова
ны
с
помощью
этой
зависимости,
в
результате
ч
его
получена
функция
нормального
распреде
ления
(Х)
с
ппрпметр
а
ми
:
-среднее
,
- 0.0132
-ста
ндартное
отклонение
- 0.938
-минимум
- 2.
15
-максимум
- 2.1
При
нормали
з
пции
данных
удалена
"урагatшан
"
проба
- 2.34%.
Среднее
значение
близко
к
О,
а
СКО
(среднее
квадраТИЧllо
е
отклонение)
-
к
1.
Таким
обра
зо
м,
мы
получили
из
наших
данных
нрактически
чистое
нормальное
распределение.
На
следующем
шаге
с
номощыо
программы
УЛRОВ
по
нормализованным
данным
были
построены
экспериментальные
Вl1риограммы
для
нескольких
н
а
правлений,
которые
покnзали
ИЗОТРОПНОС'fЬ
массива
в
данной
плоскости.
К
вариограммам
подобрана
изотропная
сферическая
модель
с
лараметрами
:
Со=0
.
5,
Сl=О.4,
A=180
м
.
На
следующем
этапе
программа
SJMUL,2
моделировма
"нормализованные"
зна
чения
соде
ржаний
меди
R
точках
регулнрной
сети
15*15
м,
имеющие
то
же
ра
спределенИi~
и
вариогра
мму
,
что
и
ие
одные
данные.
В
итоге
мы
получили
972
смодеЛI1РОВ
'
НIIЫХ
значения,
имеющих
нормальное
распределение
с
характерис
т
иками
:
-среднее
- 0.0]
58
-СТ.отклонение
- 0.9357
-минимум
- -2.938
-максимум
- 3.0
По
этим
данным
БЫЛ1l
постро
ен
I
экспери
м
ентаЛЫ-l
ые
вариограммы
для
основных
направлений
,
кот
рые
хорошо
соглаСОВblВал
ись
с
заданной
моделью
.
В
этой
ситуации
не
тре
бовал
ось
"обусловливан
и
е"
значений
в
точках
опробования
исходными
"нормализованными"
данными.
В
заключении
программ
а
JТGAUSS
пр
е
обра
зо
вала
полученн
ое
нормализованное
множество
данных
в
распределение,
соответствующее
распределению
исходных
данных,
вновь
исполь
зу ~
ФУJlКЦИЮ
Y=f(X).
6.2.2.
Экономнческая
OI~eHKa
запасов
уранового
месторождення
На
последней
стадии
деятельности
геологов,
когда
рудопрояв.ление
обнаружено,
пробурено
нескольк
о
скважин,
определяющих
основные
характеристики
рудного
,тела,
необходима
оценка
э
к
ономи
чески
целесообрnзных
запасов,
ко
торые
можно
и
влечь
из
данного
месторождения
.
Обычно
экономические
ограни'ICНИЯ
опредеЛЯlОТСЯ
борТ()вым
содержани
е
м
,
поэтому
для
оuенки
и
J3лскаемых
за
п
асов
достаточно
определить
пропорцшо
(долю)
блоков
Я'4
е
истой
модели
запежи,
имеющих
содержnние
выше
бор
тов
ого
.
132

Однако,
в
реалыIйй
СI1ТУЩ.1ИИ
иногда
существуют
'
с
е
рье
з
ны
~
трудности
с
IЮ8JIе'IGнием
некоторых
отдельно
распо
л
оженных
выемочных
блоков
6
отработку,
особенно
на
подземны
х
рудниках.
Чтобы
проиллюстрировать
эту
проблему
и
показать
,
как
можно
ее
решить
с
помощью
условного
моделирования,
рассмотрен
горизонтальный
пласт
ПОСТОSlнной
мощности
(5
М),
который
содержит
ИЗW1екаемые
концентрации
урановой
руды
в
некоторых
частях
пласта.
Размеры
пласта
1200*800
м.
Он
разоедан
небольшим
КОJlичеством
скважин
по
сетке
100*50
м.
Статистический
анализ
данных
опробования
показал
логнормальное
распределение
со
средним
содержанием
ИЗ
()в
-
0.02%
и
коэффициентом
вариации
-
около
140%.
Анализ
вариограмм
позволил
подобрnть
к
массиву
'
анизотропную
сферическую
модель
с
параметрами:
эффект
самородков
-
О.зс
(где
С -
порог
вариограммы)
,
зона
W1ияния:
минимальн
ая
200
м
в
северо-восточном
напраW1ении,
максимаТlЬНая
400
м
в
перпендикулярном
северо-зашщном
напраW1ении.
Борт
о
вое
содержание
Из
08
для
небольших
блоков
камерно-столбовой
системы
разработки,
действующее
во
nремя
оцr.нки
-
0.03%.
Если
ориентироватьсн
только
на
распределение
сод
е
рж
а
ний
по
данным
опробования,
то
по
известному
бортовому
содержанию
можно
рассчитать,
'11'0
ЛИШЬ
17.5
%
пересечений
являютс
я
кондиционными
.
С
учетом
средней
ruiотности
руды
2.6
т/куб.м
получается
ко
л
ичество
ИЗW1екаемых
запасов
- 2.272
млн
тн
со
средним
содержанием
урана
0.
06
%.
Однако,
эти
цифры
ЯW1ЯЮТСЯ
только
верхним
пределом
,
т.к.
при
этом
предполагается,
что
псе
запасы
с
КОНДИЦИОННbJМИ
пересе'Jениями
могуг
быть
отработаны.
Это
может
быть
достигнуго
ЛИШЬ
при
открытой
разработке,
но
часто
трудно
достижимо
на
подземных
работах,
где
ДJlЯ
I:iСКРЫТИЯ
некоторых
кондиционных
зон
требуется
проходк
а
дополнитеЛhНЫХ
дорогостоящих
подземных
выработок
.
Для
рассмотрения
этих
пространственных
лроблем
было
использовано
условное
моделирование
концентраций
у
р
'
н
а
в
пр
е
делах
пласта
по
сетке
20*20
м
.
На
к
а
рте
смоделированных
величин
оконтурипали
с ь
кондициuнные
рудные
зоны
.
Так небольшие
включения
руды
на
во
с
точной
сторон
е
участка
и
меЖдУ
двух
зон
исключены
и
з
ПОДС
'
l
ета
кондицион
н
ых
запасов,
т
.
к
.
они
находятся
слишком
далеко
от
основн
о
й
зоны
минерализации
.
Такая
дополнительная
сортировка
и
исключение
трудноизмекаемых
запаСО
D
сдвигают
границу
между
р
у
дой
и
нородоН,
табл.6
.
2.
В
таблине
первые
3
строки
получены
в
РСЗУЛI.тате
условно
г
о
моделирования,
а
по
'ледюlЯ
..
ею
данным
расп
.IедеJJеJfЮI
исходных
проб.
Видно,
'11'0
МОДG.1Нlрованис
существенно
уменьшило
тоннаж
до
ст
у
п
ной
ДШ
I
добычи
руды
,
а
л
дователыю
и
запаСbJ
металла
по
у'шстку
.
1
.з

Табл
.
6.2
о
ценка
извлекаемых
за
пасов
урана
Запасы
Руда
+
порода
Руда
Порода
Тоннаж
%
U308
Тоннаж
%
U308
Тоннаж
Северная
1.
83
млн
т
0.052
1
.
2млнт
0.07 0.63
млн
т
З0на
Южная
1.03
млн
т
0.036 0.
52
млн
т
0.054 0.51
млн
т
З0на
Bcero
2.
86
млн
т
0.046 1
.73
млн
т
0.065
1.
14
млн
т
Оценка
2.27
млн
т
0.066
распреде-
ления
6.1.3.
Экспериментальная
оценка
и
зме
нчивости рудопот
ока
..
а
обогатительную
фабрику
.
%
U308
0.
017
0.017
0.017
Возможность
моделиров~ния
ха р
акте
рис
тик
руд
ы
по
регулярной
сетке
с
малым
шагом
ПОЗВOJUlет
впосл
едствии
имитировать
формирование
из
этих
ячеек
рудопотоков, поступ
ающих
из
карьера
или
шахты
на
обогатительную
фабрику
.
Ц
елью
этих
операций
ЯВJlЯется
оценка
влиниия
р
азмеров
обор удования
и
последовательности
И:Jвлечения
запасов
на изменчивость
качества
руды,
поставляемой н
а
переработку.
Ус
ловное
моделирование
здесь
используется
для
генерирования
возможных
характеристик
руды,
например,
в
ежедневных
объемах
добычи
о
дног
о
забон
.
Затем
эти
смоделированные
значения
объединяются
в
це
почки
рудопотоков
ДJШ
заданного
периода
времени.
Н
иже
р
ассмотре
н
пример
карьера,
разрабатывающего
медно
ПОРфИРИТ080е
месторожден.ие.
Высота
уступа
12
м
,
а
опробование
руды
на
соде
рж
ание
меди
ведется
по
шламу
буровзрывных
скважин
на
всю
мощность
уступа.
Распределение
меди
по
данным
геологоразведки
-
J10гнормальное
со
средни
м
- 0.
51
%
и
ко
э
ффициентом
вuриации
- 95%.
Рассматривались
2
варианта
используемого
оборудования:
-2
экскаватора
с
ковшом
емкостью
8
куб
м
каждый,
работ
а
ющ
их
на
2-х
разных
уступах
одновременно;
-1
экскаватор
с
ковшом
емкостью
15
куб
м
,
работающий
на
одном
уступе.
В
первом
случае
ежедневно
отрабатывается
2
блока
р
а
змерами
1
5х
7
.5х
12
м
на
ДВУХ
горизонтах,
а
во
втором
случае
отрабатывается
один
блок
размерами
15х15х12
м
.
Так
как
значения
содержа
ний
в
последовательности
смежных
блок
ов
коррелированы
,
то
можно
ожида
т
ь
большей
изменчивости
в
рудопотоке
большого
экскават
ора
.
Ч
т
обы
оценить
эти
предп
о
ложения
количественно
бьuIO
выполнено
моделирование
уступных
содержаний
м
ед
и
rю
регулярной
сет
ке
7
.5х7.5
м
.
После
этого
моделировался
рудопоток для
2
-
х
указанных
вариантов
.
В
первом
случае
за
о
днодневную
порцию
приним
ал
о
сь
среднее
значение
2-х
смежных
ячеек
модели,ВО
втором
-
сре
днее
з
нач
ен
и
е
кв
адра
тног
о
блок
а,
состоящего
из
4
-
х
ячеек
.
1
3"1
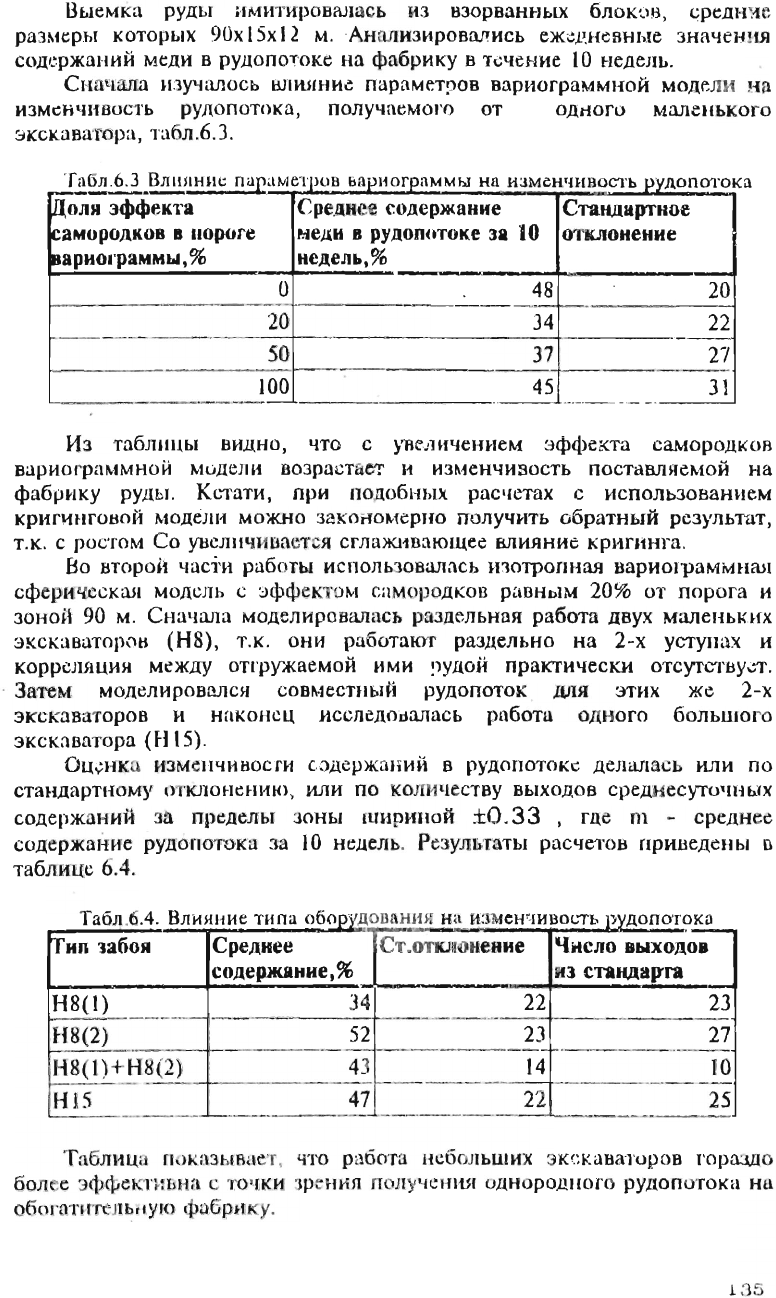
Выемка
руды
имитировалвсь
из
взорваНt-Jых
блоко»,
<;редн
1Ie
размеры которых
90х
15х
12
м.
Анализировались
еж,-:дневные
значения
сод
е
ржаний
меди
в
рудопо
токе
на
фабрику
в
течение
1
О
недель.
Сначала
изучалось
влияние
параметров
вариограммной
модели
на
изменчивuсть
рудопотока,
получаемого
от
одного
маленького
ЭJCс
кава
ора,
та
Л
.
б.
З.
Т
б
63
В
а
(\
Л
.
.
ЛШIНИс
ПUр<lме
трuв
вариограммы
на
изменчив
ость
РУДОПОТОК
p:i;;;;-
эффекта
Среднее
содержание
Стандартное
!Самородков
в Ilороге
меди
в
рудопотоке
за
10
отклонение
jваРИШ
'
раММbI,
%
иеделlt,%
О
48
20
20
34
22
-------_
.
50
37
27
100
45
3]
Из
таблицы
видно,
'!то
с
унешrчением
эффекта
самородков
вариограммной
модели
возра
стает
и
изменчивость
поставляемой
на
фабрику
руды.
Кстати,
при
подобных
рас'(етах
с
использованием
кригинговой
модели
можно
закономер
но
получить
обратный
результат,
Т
.К.
с
ростом
Со
увеЛl\ч
и
rш
с
т
с
я
сглаживающее
влияние
кригинга
.
Во
второй
части
раб
от
ы
использоваласъ
изотропная
вариограммшш
сферическая
мод
ель
с
эффектом
сuмородк
ов
равным
20%
от
порога
и
зоной
90
м
.
Сначала
моделировалась
разд
ел
ьная
работа
двух
маленьких
экскаваторов
(Н8),
Т.к
.
они
работают
раздельно
на
2-х
уступах
и
корреляция
между
ОТI
'
ружаемой
ими
рудой
практически
отсутствует
.
.
Затем
моделировалсSl
совместный
рудопоток
для
этих
же
2-х
экскаваторов
и
наконец
.исследовалась
роБОТI1
одного
большого
экскаватора
(Н
15).
Оценк
а
из
Ме
нчивости
содержat
ий
в
рудо
потоке
делалась
или
по
стандартному
о
т
клонению
,
или
по коли
ч
еству
выходов
среднесутuчных
содержаний
за
пределы
зоны
ШИРИНОЙ
±О.
ЗЗ
,
m,e
ш
-
среднее
соде
ржание
РУДОПОТОКil
за
1
О
недель
.
Результаты
расчетов
приведены
n
таблице
6.4.
6
В
Табл
. . 4.
б
лияние
типа
о
ор
у
доnания
на
изменчИlЮ(.'ТЪ
рудолотока
ГГип
забоя
Среднее
СТ
.
ОТКJI
нение
Число
выходов
содержание,%
нз
стандарта
Н8(1)
34
22 23
-'-
.-
Н8(2)
52
23
27
--
--
--
-
----
-
.
_---
-
---
Н8(1)+Н8(2)
43
14
10
----
-
1-
'
-
----
H15
47 22
25
--
'--
._.
-
ТаБЛИЦе
n
t\ЗhlRuе
т
,
то
Р
"
бота
н
-боль
ших
эк(
:
каваторов
гораздо
бол
е
э
ффек
'
~ш
на
с
ОЧКИ
зр"нi'iЛ
ПОllУtlt~НИЯ
одн
POДlIOI
'
O
рудопо'Гока
на
оБОГ3ТlfтеJ1~IIУIO
фабрику
.
1
35

6.2.4.
Полное
условное
моделированне
ypasloBoro
месторождения
l
Уже
десять
лет
хорошо
известно, что
модели
ру.дных
тел,
предназначенные
для
оценки
запасов,
не
могуг
быть
успешно
использованы
ДТlЯ
nлаНИРО8i1НИЯ
горных
работ
.
Та кже
всем
известно
,
что
дисперсия
содержаний
в
блоках,
оцененных
кригингом,
меньше
чем
дисперсия
реuльных
содержаний
этих
блоков
.
Следовательно,
использование
кригин-говых
оценок
при
составлении
плана
отработки
будет
приводить
к
ошибочным
заключениям.
Правда
в
некоторых
случаях
эти
2
дисперсии
могуг
быть
почти одинаковы,
но
это
произойдет
только
тогда,
когда
дисперсия
оценки
а;
будет
очень
мuла,
а
месторождение
разведано
по
очень
плотной
сети.
Рассматриваемое
месторождение
урана
разбурено
по
сетке
25х
1
О
м
и
в
некоторых
случаях
еще
tН1ще.
Содержания
ИЗ
08
(в
дальнейшем
-
урана)
варьируют
от
следов
до
50%,
что
означает
необходимость
специальных
мер
по
радиационной
безопасности
при
отработке
месторождения.
Кроме
того,
в
породах
встречается
мышьяк,
вызывающий
необходимость
принлтия
дополнительных
мер
безопасности
при
планировании
горных
работ.
Предполагалось,
что
условное
моделирование
может
помочь
с
некоторыми
из
этих
проблем
.
МеТОДОIlОГИfJ
этого
моделирования
известна
давно,
однако
практиче
с
кое
его
исполь
з
ование
требует
иногда
использования
специальных
ПРllложений
как
в
данн
ом
случае.
Месторожденне
Рассматриваемая
зuлеж:ь
расположена
в
Канаде
и
ОТНОСИТС}I
к
урановым
месторождениям
с
несогласным
напла
ст
ованием
.
Залежь
простира
етс
я
в
длину
на
1400
м
,
в
ширину
- 8
среднем
на
15
м
,
достиг
ая
в
наиболее
широкой
части
-
50
м.
Глубина
залегания
50
-
80
м
о
т
поверхности.
Такая
очень
узкая
и
вытянугая
форма
рудного
тела
накладыва
ет
специальные
требования
к
моделированию.
Программа
опробо
ван
ия
включала
бурение
477
кер
н
овых
скважин
по
сетке
25xlO
м
11
меньше,
получение
и
исследов
ан и
е
н
а
уран,
никель
и
МЬШIЬЯК
30
l'ЫС$lЧ
РJЩОВblХ
проб
длиной
0.3
м.
Среднее
соде
р
жание
урана
свыше
2%.
Тре
бования
к
моделн
Моделирование
в
данном
с
л
учае
должно
ВЬUlвить
даже
OtleHb
слабую
колеблемость
содержаний,
Т
.
К.
разведка
выполнена
по
д
ост
аточн
о
плотной
сети.
Структура
и
змен
чивости
предполагается
·
одинаковой по
всему
месторождению,
п
о
этому
моделирование
обычно
выполня
ется
на
одном
из
его
наиболее
характерных
участко
в
.
В
данном
случае
оно
реализовано
на
участке
длиной
600
м
п о
простиранию
в
центрально
й
части
месторождения.
Мо
дел
ировали
сь
соде
ржания
урана
и
мышьяка
по
регулярной
с~и
2х2х
l
м.
При
эт
ом
брuлась
в
учет
плотно
сть
руды
для
пересчета
объемо
в в
тоннаж
при
определении
извлека
емых
за
п
асо
в
.
Р
аз
верн
утое
описан
и
е
этоro
ПРШfсра
дано
11
р а
боте
1
41
13
6

Из-за
очень
узкой
формы
змежи
требовалось
также
моделиров.:lt
и
е
формы
минерализации.
Принималось
в
расчет
также
ПОDышеннал
изменчивость
мин
ерш
IИ
З
.:ЩИИ
И
наибольшая
густ
та
разведочных
скважин
в
районах
с
высоким
содержанием
урана.
Количество
моделируемых
очек на
х
дилось
в
районе
200
тысяч.
Таким
образом
,
ИМt
J
ЮСЬ
2
задач
и
:
моделированне
контура
минерализации
и
модслировuние
кuчества
урановых
руд.
Вторая
з:щача
более
сложная
и
свюана
с
цел
ым
рядом
проблем,
рассмотренных
ниже
более
подробно.
В
чаСТIIОСТИ
речь идет
о
проблемах
учета
плотности
руды,
'
одновременного
моделирования
содержаний
урана
и
мышья
'а,
нормализации
да
нных
11
некото
рых
других
.
ПроБJlемы
ра
зm
,чи~
между
рудой
11
ПОРОДОЙ
И
моделирование
кшп')'ра
ми
lерализацми
Гистограмм
а
сод
ржания
урана
по
9656
композициям
длиной
1
м
ПОК!lЗ
'
па
одну
вершину
и
долю
некоЩЩЦИОННЫХ
запасов,
состаwшющую
2/3
от
всех
ЗЩJaСОВ
.
Эти
не
онд)щионньн~
КОМПОЗИЦИИ
доми
н
ируют
В
распределении,
хотя
t
аиболеt
важное
значение
имеют
композиции,
связанные
с
минерruш
ациеЙ.
Кроме
того,
распределение
сильно
скошеНо
влево,
и
нормализация
его
будет
достаточно
трудным
делом
.
По
этой
причине
было
принято
решение,
что
данные
должны
рассматриваться
как
2
различные
популляции:
минерализованная
-
с
содержаниями
уран
а
выше
0.005%
инекондиционная
-
с
содержаниями
до
0.005%.
Контур
минерализации
определяется
оцсниванием
вероятности
того
,
что
данная
точка
сети
2х2х
1
м
минерализована
.
Эта
оценка
.
получается
кри
г
ингом
(;
помощью
индикаторной
переменной,
имеющей
значеН
.
ие
О
-
.lЩЯ
1
ороды
И
1 -
для
руды
.
Забракованные
точки,
индикаторы
которых
находятся
между
О
и
1
также
учитывались
в
оценке.
Возмо>.шо,
на
пример,
что
точка
расположенная
рядом
с
центром
Рудного
тела,
индикатор
которой
0.9,
могла
быть
отнесена
к
породе,
если
случайн
ая
величина,
с
КОТОРОЙ
она
сравнивалась,
находится
между
0
.9
и
1.
Это
показывает
,
что
кригинговая
оценка
0.9
в
данном
случае
означает
90%
вероятности
минерализованности
даннои
точки.
Таким
же
образом,
если точ
к
а
на
ок
раине
рудного
тела
имеет
индикатор
0.1,
то
это
говори
т
о
10%
вероятности
ее
минерализова
шо~ти.
Так
как
контур
минерализации
аким
образом
был
определен,
то
последующее
моделироnnние
СQдержаний
ПРОJ1ЗвоДилось
только
в
этом
контуре.
Точки
за
пределuми
контура
в
дальне
й
шем
не
рассматривались.
Выполнение
р&боты
Перед
выполнением
операции
кригинга
должны
были
быть
построены
кспериментальные
индикаторные
вариограммы
и
выбрана
соответствующан
модель
.
Цель
кригинга
определить
контур
минерал
и
ации,
поэтому
важно
было
удапить
некондиционные
(с
индикатором
равнь
м
О)
КОМПОЗIЩИИ,
далеко
удаленные
от
местор
ожде1-lИЯ.
137

с
помощью
созданнои
ранее
ОЦtliOlJНОИ
модеJlИ
с
блоками
размерами
225х
10х4
м
может
быть
построен
ореол
мокруг
зоны
мин~рализации,
которым
сокращается
чрезмерное
l<ОJ1ичество
породных
композиций
за
пределами
м
сторожде'iИJI.
Таким
обра
ом,
в
контурах
моделируемой
зоны
осmлось
только
575
рудных
блоков,
в
преде
лах
которых
были
рассчитаны
экспt:РИМСIIТ:1льные
вариогра
ммы
и
проведена
кригингоная
оценка
.
Экспе
римент
альные
вариограммы
раССЧНТblВались
по
индикаторным
значе
ниям
0-1
в
оне
опро
ования.
По
ним
бъmа
подобрана
сфеРJfческая
модель
с
геометрической
анизотропией
и
параметрами:
Со
=
О.14,
Сl=0
.
1,
А(З
-
В)
=
11
2
.
5
м,
А(С-Ю)=20.0
м,
А(вертикаль)=30.0
м.
Зоны
влишшя
окuзались
одинаковыми
независимо
от
тип"
используемых
ДЛЯ 1
остроення
ваР~ЮJ'рамм
исходных
данных:
реальных
или
моделируемых.
.
Область
поиска
проб
при
paCtteTe
кригинга
была
задана
в
виде
прямоугольного
параллелепи
педа
с
размерnми
27х
12х
1.5
м.
ОКончателt.ные
результаты.
Контур
подсчета
запасов
содержит
184
555
точек,
расположенных
на
регулярной
сетке
2х2
'1
м
.
Из
них
178
2
47
точки
бьU1И
успешно
оценены
кригингом,
а
оставшиеся
не
имели
D
зо
н
е
поиска
необходимого
количества
проб
АЛЯ
оценки.
Было
выполнено
сравнение
КРИГIIНГОDЫХ
величин
и
индикаторных
переменных
для
большинства
точек,
которое
дало
положительные
результаты.
На
~аключител
ьном
этапе
составлены
погоризонтные
кuрты
минерализации,
которые
получили
удовлеТlюрительную
оценку
геологов,
хорошо
знающих
месторождение.
ПроБJtемы,
связанные
с
моделироваllием
качества
ура.юноЙ
руды.
Плотность
руд
связана
с
содержанием
в
ней
MeтaJUIOB
и
имеет
сильную
изменчивость,
как
и
изменчивость
содержаний.
Поэтому
для
корректной
оцеНЮ1
тоннажа
необходимо
знать
плотность
руды
в
каждой
точке
регулярной
сети
модели.
По
большинству
имеющихся
проб
плотность
в
сухом
состоянии
не
опредеmшась,
и
лишь
по
некоторым
им
е
лись
данные
о
плотности
во
влажном
состоянии.
Поэтому
бьU1
пров
е
ден
регрессионный
анализ
,
с
помощью
которого
расчет
плотности
руды
производился
по
содержаниям
в
ней
металлов
.
Когда
имелись
данные
по
плотности
во
влажном
состоянии,
то
пересчет
делался
11.0
уравнению
регрессии,
полученному
для
проб,
име
ющих
данные
по
обеим
видам
плотности,
Далее
рассматриваются
проблемы,
связанные
с
Ilеравномериым
опробованием
месторождения.
Исходные
0.3
м
пробы
по
вертикали
композировались
по
дЛине
1
м
с
помощью
простого
взвешивания
.
По
горизонтали
плотность
информац
ии
также
нерегулярна
.
Имеются
4
зоны
с
повышенными
содержаниями,
где
опробо
в
ание
делмось
более
часто
.
Такая
кластеризаЦИJl
приводит
к
з
авышению
с
редне
г
о
содержания
и
дисперсии
по
месторождению.
1 3 8

Смоделиров
'
нные
на
регулярной
сети
точки
долу.сны
.
иметь
распред
еление,
соответстоующее
правильному
(несмещенному)
распределению
проб по
месторождению.
Чтобы
найти
это
р
аспределение
необходим
о
было
декластеризовать
имеющееся
множество
композиций
проб.
Есть
много
способов
для
этого.
В
частности
можно
разделить
все
месторождение
на
равные
квадратные
зоны
и в
каждой
зоне
оставить
(случайным
выбором)
одну
пробу
.
Там,
где
имеетсSl
всего
одна
проба,
она
оставляется.
Надо
иметь
в
виду,
что
существенное
влияние
а
сгатистические
показатели
имеет
размер
блока
(зоны).
Так
блок
25х25х4
м
дал
среднюю
оценку
содержания,
01ыtчающуюся
на
40%
от
среднего
значения
массива
реальных
проб
.
Для
расчетов
был
использован
блок
размерами
10х5х2
м,
который
дал
средний
показатель,
очень
БШfЗКИЙ
к
среднему
содержанию
модели
запасов
месторождения
.
После
такой
деКlIасте
ризации
осталось
1480
композиций.
Таким
образом
былн
получены
"реальные"
ЛОГНОРМШIьные
распредеJlения
содержаний
урана
и
мышьяка.
для
того,
чтобы
одно
временно
моде.rпtровать
в
точках
регуляриой
сети
содержания
урана
и
мышыжа,
рассчитаны
регрессионные
уравнения,
связывающие
норммизованные
параметры.
Эти
уравнения
использовались
непосредственно
при
моделировании
в
результате
чего
получалис
ь
сра
у
оценки
двух
содержаний.
Так
само
моделирование
осуществлялось
применительно
к
факторам,
I1З
которых
в
дальнейшем
вычислялись
значения
содержания
урана
и
МЫШЫIка.
Эти
факторы
определялись
из
уравнений:
F
1
=
~
J 1 2_
p
(-
As
n
+
ИзОSп),
F 2 = t J 1
2+
p
(+As
n
+
ИзОаn
(6.1)
где
р
-
коэффициент
корре
JU
IЦИ
И
нормализованных
содержаний
A~
I
I
ИЗ
ОВп
.
Нормализаuия
с
помощью
полиномов
ЭРМJ.lта
использовалась
для
получения
Гауссового
распределеНI1Я
моделируемых
содержаний.
Хотя
эта
процедура
хорошо
ИЗllестна,
тем
не
менее
встретились
проблемы,
которые
потребовали
де
т
ального
рассмотрения.
Такие
проблемы
как
выбор
между
применением
"сырых"
или
ло
г
арифмированных
данных,
обосноваllие
ч
исла
коэффициентов
пол
и
н
о
мов
Эрмита
и
т
.
д.
Кроме
того,
большое
количество
малых
и
н
улевых
значений
содержаний
в
массив
данных
также
з
атрущН1Ю
Т
н
ормализацию
.
Поскольку
начальное
распределение
логнормальное,
ТО
л
огарифм
и
рование
исходных
данных
позволяет
облеГЧI1ТЬ
решение
большинст
ва
персчисленных
проблем.
В
результате
БЬVIа
подобрана
модель
с
1
О
коэ
ффициентами,
которая
достаточно
точно
I1реобразовывала
логарифмированн
ые
исходные
дан
-{ые
в
н
)рмanьное
р
а
спределеllие
со
средним
=
О
и
стандартным
отклонением
= 1.
Моделироваt.ие
Эта
Г
J
Шl.lЮUI
СТ[Щ1tiI
работы
осущеСТВЛSlл
ас
ь в
3
этапа:
-
МО
С
J
шров
а
ни
е
ф
а
кторов
;
-об
У
СJННI
.
IНIВЩНlе
фак
'
юр
о
в
с
целью
использования
фактических
зн
а
ч е
НI1Й
пр
о б
;
lЗU
