Капутин Ю.Е., Ежов А.И., Хейнли С. Геостатистика в горно-геологической практике
Подождите немного. Документ загружается.


нового
MaC
C~Ba
рассчитывается
вар
иограмм
а
и
выполняется
процесс
линейного
'
кригинга,
КОТОРЫЙ
будет
выдавать
оценки,
лежащие
в
интервале
О
-
1.
Эти
оценки
могуг
Быьь
интерпретироваНbj
как
значения
вероятности
того,
что
среднее
содержание
оцениваемого
блока
-
ниже
бортового.
OCIIOBHoe
преимущество
индика
то
рного
кригинга
в
том
,
что
распределение
реальных
данных
предварительно
превращается
в
простое
дискретное
распределение
с
известными
свойствами.
Коне
чно,
и
в
эт
ом
случае
необходимо
предварительно
рассчитать
вариогр
аммную
модель
для
индикаторных
величин.
Естественно,
что
много
информации
теряется
при
получении
индикаторной
кригинговой
оценки,
которая
позволяет
лишь
судить,
находится
ли
оцениваемый
параметр
д
ан
но
го
блока
выше
или
ниже
единственного
заданного
значения
бортового
содержания
.
Чтобы
получить
реальные
оценки
переменной,
необходимо
выполнить
ра~четы
для
достаточно
большого
количества
вариантов
бортовых
содержаний
И
р
асполагать
оценками
парам
ет
ров
локального
распределения.
А
эт
о
в
свою
очередь
т
р
ебует
предварительного
рас
ета
и
инТерпретации
большого
числа
вариограмм.
При
н
е
которых
обстоятельствах
в
процессе
интерпретации
вариограмм
могуг
получаться
бессмысленные
результаты
,
наприм
ер
при
более
высоком
"борте"
количество
некондици
онных
блоков
может
ОКI\
ЗI\ТЬСЯ
меньше,
чем
при
меньшем
бортовом
содержании
и
т
.
п
.
Индикаторный
кригинг
имеет
и
более
'
серьезные
проблемы.
Поскольку
индикаторы
имеют
значения
только
О
и
1,
по
этому
они
имеют
дискретное
распределение
в
е
роятности
,
а
ме
т
одоло
гия
кригинга
требует
непрерывного
р
аспределения
(
и
более
то
о,
распределенин
с
определенными
свойствами).
Таю
м
образом
,
правомерность
использоваНИSI
индикаторного
к
ригинг
а
наХОДИТ
С)"
1
под
большим
вопро
сом.
Бе
скр
uzuн
гоtlые
методы
С
.
появл
ением
теории
пространственных
переме
н
ны
:х
и
ее
практических
пр
иложений
в
виде
вариограммного
анализа
и
кригинга
другие
методы
моделирования
запасов
поле
:
шых
и
копаемых
стали
lIемодными
.
Тем
не
менее,
не
оторые
нс-геостатистические
методы
давали
отличные
ре
з
ультаты,
несмо
т
ря
на
кажущееся
несоверо
снство
теории
и
в ряде
случаев
-
на
явное
полу"ение
ими
смещенн
IX
оценок.
Простейшие
из
этих
методов
используют
элемента
рные
геометрические
построения
.
Один
из
них
работает
с
сетью
тр
еугольников,
соединяющих
двухмерное
множество
точек
данных
(например
-
пересечения
скважинами
I1JH1CTa
или
жилы),
с
помощью
которых
(пр
иведением
задачи
к
плоскому
виду)
р
ассчиты
вает
ся
объем
.
руды и
содержание
в
ней пол
зн
ы
х
компонентов.
Другой
метод
со
здает
МНОГОУl
'ОЛЬНИКИ
вокруг
каждой
т
о
чки
данных
и
просто
экстраполирует
значение
переменной
в
TOtlKe
на
всю
окрестность
.
Оба
эти
метода
слишком
чувствительны
к
распределению
точек
исходных
данных,
а
получаемые
с
помощью
них
результ
аты
имеют
смеl.Цение
и
отличаютсн
в
худшую
сторону
от
соответствующих
геостаТJ1стически'Х
меТОДОD.
Более
развитые
методы,
получившие
широкое
распространение
с
появлением
компьютеров
,
обычно
включают
в
l.:еБJr
трепд-анализ,
который
стал
стандартным
приемом
для
моделиров
а
ния
простых
1
60

геологических
структур
(с
помощью
несложны:х
матt:мати
~еских
Функций)
в
нефТj[НОЙ
геологии.
Моделирование
методом
скользящего
среднего
стало
стандартным
методом
оценки
запасов
руды
в
разведочной
геологии.
Линейный
кригинг
явля
ет
ся
особым
случаем
этого
метода
.
8.3.
НепарамеТРИ'lеская
геостатистика
Поскольку
Теорин
Пространственных
ПеременнbJX
развивалась
в
KOH~KCTe
(по
праВI-U1ам)
параметрической
статистики,
то
она
тр
е
бу
ет
особых
свойств
ПОПУЛllЯЦИЙ, к
которым
она
применяется.
Главное
требование
-
нормальное
распределение
исходных
данных
.
(ми
хотя
бы
нормальное
р
ас
пре
де
ление
значения
ошибки)
и
стационарность.
Эти
требования
распространя
.
ются
на
все
области
рассматриваемого
пространс
т
в
а.
Существует
и
третье,
менее
известное
требовани
е
-
все
рассматрива
е
мые
пер
е
менные
должны
быть
аддитивиыми,
Т.е.
теория
пространственных
nepeMeHНbIX
и
производные
из
н
е е
методы
действительны
только
для
тех
переменных,
для
которых
простое
алгебраическое
сложение
я.вляется
допустимой
операцией
.
это
требование
и
скл
ючает
использование
многих
геофи
з
иче
ских
переменных
'
полученных
в
полевых
условиях,
и
таких
~рои
з
во
дных
параметров
,
как
пористость
и
проницаемость,
а
также
отношения
(например
C
U/ZI1)
.
и
геохимические
концентрации
или
содержания
минералов
без
СВflЗИ
по
следн
их
с
массой
обра
з
ца
или
оц
е
нив
ае
мого
блока
.
Мо
д
ифицированные
геостатистические
технологии,
изобрет
е
нны
е
с
ц
елью
обойти
требования
нормального
распре
де
ления
и
стационарности
(Та
б
л
.
8.1.),
на
самом
деле
не
действую
т в
эт
их
ситуац
ия
х.
Они
ино
гда
дают
хорошие
результаты
,
когд
а
одно
требование
(из
перечисленных
выше)
нарушается,
в
то
время
как
другое
-
соблюден
о
.
Если
н
е
соблюдаются
оба
требования,
то
геостатистикu
здес
ь
бессил ьна
.
Табл.
8.1.
УСЛОDИН
ИСПОJlъзо
в
ани
н
различных
видов
Кри
гин.га
для
оц енки
за
па сов
РАСПРЕ
-
ЩЕJlЕНИЕ
Сложное
Дизъюнкт
ивный
? ? ?
Кригинг
Простое
,
Логнормальнь
й
? ?
?
изв
ест
ное
,
Кр
иг
ин
г
наприм
ер
-
lriогн
о
рмальн
ое
ЛИllейный
У
нин
ер
-
Обобщен
-
'!
Нормально
е
К
риг
инг
сал
ьн
ь
й
ная
Кригин
г
ко
вар
и
ация
::J
СТАЦИОНАР
-
Ст::щионарн
)С1Ъ
Про
стой
Ме
ст
н
ые
С~
U1Ь
Ная
НО
С
ТЬ
:
тренд
тренды
utlизотr
ю
-
пи
я
=
16].

ДРYl'ая
проблема
имеет
отношение
к
используемым
масштабам
измерений.
Геостатистика
Криге
и
Матерона
тесно
связана
с
обычной
параметрической
статистикой
и
требует
HellpepblBHbIX
поинт~рвальных
измерений
.
Геостатистика
не
может
l~oppeKTHO
обрабатывать
ПОСllеll.овательные
(раНЖИРОlШНllые)
измеренин,
т
.
к.
концепция
дисперсии
lIВJUlетсл
центральной
в э
той
теории
,
а
многовариантная
дисперсия
не
может
быть
Р<lссчитана
по
ранжированным
значениям.
Далее
rlОнвляетсл
следующая
проблема
:
даже,
если
основное
множество
данных
существует
в
виде
поинтервШ1ЬНЫХ
юмсренИI
'
,
а
некоторые
значениSl
записаны
в
виде:
"ниже
установленной
границы"
или
"следы",
то
последние
не
являются
представителями
деиствительных
значений
переменной
в
норм:шьном
масштабе
измерений
(Рис.
8.1),
а
следовательно
в
итоге будет
получено
урезанное
распределение.
В
настоящее
время
имеется
несколько
новых
методов,
которые
могуг
быть
использованы
для
оценки
или
интерполяции
поверхностей
по
пространственно
распределенным
данным
без
CTpol
'
oro
соблюдения
описанных
выше
ограничений,
характерных
ДJШ
стандартных
геостатистических
методов.
Они
имеют
про'шое
теоретическое
обоснование
и
свободны
от
серьезных
недостатков
методов,
используемых
до
появления
геостатистики.
Во
многих
непараметрических
методах
первым
шагом
является
преобразование
исходных
данных
в
ранги,
Т
.
е
.
превращение
интервального
представления
данных
8
ПОРЯДКОI:IЫЙ.
Принципиальное
преимущество
этой
процедуры
заключаеТСJJ
в
том
,
что
здесь
происходит
автоматическое
преобразование
любого
ис
х
одного
распределения
D
простое
однородное
распределение
с
хорошо
известными
и
изученными
свойствами.
Оценкой
центра
получ
е
нного
распределенин
теперь
будет
медиана
-
Т.е.
величина,
которан
делит
распределение
на
2
равные
части.
Там,
где
исходное
распределйще
бьulО
нормальным
,
медиана
и
среднее
значение
6уду-с
совпадать,
но
медиана
в
~TOM
случае
будет
менее
эффективна
в
качестве
оценщика,
т.к.
информация
частично
теряется
при
переходе
от
интервального
к
ранжированному
представлению
исходных
данных
.
Однако, ДЛН
многих
других
распределений
медиана
является
лучшим
оценщиком
чем
среднее
значение
в
том
смысле,
что
она
бол
е
НЩJ.ежнп
и
неЧУВСТВ
..
lТельна
к
экстремальным
значенилм,
которые
могу-
с
быть
ПРIIЧИНОЙ
неприлтных
неожиданностей
при
оценке
,
о
с
обенно
8
случ
а
я
'х
сильно
скошенных
распределений,
обычных
ДJ1Я
качеств
е
нных
параметров
руд
месторождениil
,e~HЫX
метал
л
ов
. .
о
Рис
.
8.
].
Ра
с
предел
е
ние
,
имеЮЩtе
н
е ОrIр
е
д
е
л
е
liНЫЙ
У
<
IaСТОК
1
62

и
среднее
11
меДШlНа
имеют
несколько
"прсвосход.ны
х"
стаТИСТИ'lеских
осо
снно
'тей,
КО
орые
не
зависят
от
р аспределе
ни
н;
однако
,
специалисты
свнзывnют
их
прежде
всего
со
средним,
Т
.К.
имеют
дело
чаще
вс
его
этим
параметром,
а
не
с
медианой
.
Наибо
лее
важное
свойство
и
с
реднего
и
медианы
(с
точки
зрения
процед
уры
оценивания)
заключаетс}!
в
минимизации
ошибки
.
Среднее
значение
миними
з
иру
ет
сумму
КВiщратов
отклонений,
а
медиана
·
сумму
абt:ОЛЮТНЫХ
отклонений
.
Поскольку
здесь
примениется
IIрерывистi.Ul
функция,
подразумевnемas
исполь
з
ованием
абсолютных
в
еличин,
то
математические
выводы
СТ:1Тltстических
методов
,
основанных
на
медиане,
достаточно
сложные.
Но
,
поскольку
на
медиане
не
.
отражается
.
воэдсйствие
экстремальных
веЛИЧJlН
инебо
льших
примесей
высоких
и
низких
значений
,
которые
неизв
ес
тны
с
большой
достоверностью
(например,
значения
-
ниже
заданной
величины),
она
может
быть
использована
в
с
и
туа
ниях,
которые
делают
нераЗУМНbJМ
ltЛи
невозможным
р
асчет
среднего
з
нач
ения
.
Метu
д
ология
,
nrюдиман
нами
здесь
не
основана на каких-ли бо
предварительных
предположениях
относительно
формы
распреД~Jlения
или
(
:
тацион
рности
данных
и
даже
не
требует
полного
множеСТn8
интервальных
данных.
Она
о
с
нована
на
первых
при
..
щипах
(
аконах)
теории
вероятностей
и
применяется
в
условиях,
ще
наиболее
приемлема
непараМ6
т
риче
с
к.
и
(,"1'аТИСТИl<а
.
Предположим
вначале
одном
рllОС
множество
данных,
например
-
геологический
или
геофизический
профиль
(Рис.
8.2).
Полагм,
что
данные
ра
пр
еделены
равномерно
в
oкн~
шириной
2r,
а
функция
"точка
"з
начение"
имеет
МОНОТОIIНЫЙ
характер,
найдем
среднюю
точху Р
окна
,
которая
будет
Я8JШТЬСЯ
медианой.
Если
рассчитать
в
данном
случае
среднее
начение
,
то
оно
в
большинстве
случаев
не
будtТ
соответствовать
д
не
вительному
значению
в
точк
е
Р
.
ОДI
ако,
мы
мож
е
м
встретить
проблему
даже
D
этом
простейшем
СЛУ'Iaе
.
Она
появляется,
когда
окно
соде
ржит
один
ЮIИ
несколько
пиков
(ВНa,LЩН)
(Рис.8
.
3)
,
а
функция
"1'оч
а-значение"
не
является
монотонн
й.
XOTIl
Р
0(,"1':.1
ТСJl
цен
т
ром
окна,
и
половина
величин
наблюдений
лежит
выше
значснш\
медианы,
знач~н
ие
в
точке
Р
-
не
являен:я
медианой
в
даНIIО
,
1
СЛУ'ше
.
Нет
оснований
предполагать,
ч
то
средне
е
ЯВЛЯ
СТСSI
более
л
у
t
lШИМ
оценщиком
для значения
в
TO'fKe
Р,
чем
в
предыдущем
Прl1мt:р
с.
В
DеЙСТRИГ~ЛЫIOСТИ
в
данном
ЛУ'lзе
им
ЯВJblет
н
кваНТI1ЛЬ
Q.
сперь
l
:ЮЗ
МОЖНО
(если
}J
не
лежит
точно
на
в
е
ршине
JU1И
вп
ад
ине)
:.щ
ать
новое
окно
дnстаточно
мал
енькое,
чтобы
убе,щггьеSI,
что
р
СООТВС
'
С
вует
медиане.
Для
эг
)го
ча
с
т
ь
Ф
н
11
ИИ
С
Р
,
R
)ш
~
дшая
о
ново
е
о
но
,
ДОJ1ЖI
-
Ш
быТ!
)
МОН
ТО
НIЮЙ.
]63

-
-------
--
Рис.
8.2.
Центральная
точка
монотонной
КРИDОЙ
является
медианой
величин
DНУГРИ
рассматриваемого
окна
Нстественно,
что
эта
операция
уменьшает
кодичество
используемых
данных
И,
следовательно,
увеличивает
величину
возможной
ошибки,
поэтому
может
быть
в
данном
случае
лучше
оценить
значение
Q.
Эта
проблема
может
быть
значительно
более
серьезной
в
случае
двух
или
трехмерных
массивов
данных.
Для
примера,
в
двухмерном
пространстве
(Рис.
8.4)
оказывается,
что
медиана
может
быть
удовлетворительной
для
какого-
то
одного
одномерного
подмножества
данных
в
одном
из
направлений
(сечение
1)
,
и
не
соответствует
другим
направлениям
(например
-
сечение
2).
Для
2
-
х
мерного
пространства
данных
наиболее
подходящим
ОЮiом
SJВJlЯетсSl
ОКРУЖНОСТЬ
с
центром
в
точке
Р.
Из
рисунка
8.5.
видно,
что
знаt(ение
в
точке
Р
в
общем
случае
не
лучшим
образом
оценивается
с
помощью
медианы
значений,
расположенных
внутри
окружности,
т.к.
площади
значений
выше
и
ниже
значения
в
точке
Р
(или
{;оответствующие
значения
равномерно
распределенных
точек
данных)
обычно
не равны.
Здесь
также
выходом
является
оцснивание
с
помощью
квантиля
Q,
и
в
этом
случае
определяется
чаt.'ТЬ
площади
пнугри
окна
со
значениями
меньшими
,
чем
значение
в
точке
Р?
Возможным
подх
.
одом
к
оценке
Q
нвлнетсн
про
верка
(топологическая)
окрестности
Р
и
обнаружение
тех
частей
внYIРИ
окружности
(иля
сферы)
вокруг
Р,
в
которых
значсlНШ
ув
е
личиваются
или
уменьшаются
по
мере
удаления
от
Р.
Это
иллюстрирустсн
на
Рис
.
8.б,
на
котором
проверены
8
направлений,
из
них
в
4
значения
умеНЬШЗkJТ
С
Я
в
направлении
от
точки
Р,
поэтому
можно
оценить
Q
как
7/12.
МСАИ8На
/
~
r
---
-----------
----
- -
Рис
.
8.3.
При
наличии
в
окне
пик
а
или
811i.1ДИНЫ
цеll
т р аль н
а
и
ТО4ка
ОЮl3
не
является
медианой

14
------
-
--
- -
--
--
-----
---
--
Ри
~.
8.4
.
Данные
в
ДByxмepHO~
простран
стве
·
и
Met:TCSI
ерье
:
ннш
проблема
в
практическом
использов
а
ниtl
ЭТhХ
IlРИНЦИJ10В.
Естестненно,
что
значение
в
точке
Р
неизвестно
и
явля
\,;н
цель
ю
наш
е
й
оценки,
а
определить
увеличиваются
или
умеllЬШ.
ЮI'СН
значения
при
удалении
от
Р
очень
тРудно.
Однако,
для
~
'
юго
существует
возможный
статистический
подход.
Если
все
наблюдения
ранжировать
в
соответствии
с
их
расстоянием
от
Р
,
то
можно
рас
считать
неп
араметр
ический
ко::,ффициент
корреmщии
между
этим
расстоянием
и
значениями
веJlИЧИН.
С
этой
целью
наиболее
удобно
использовать
коэффициент
корреляции
Кендалла
.
Каждая
пара
наблюдений
при
этом
сравнивается, и
в
случае,
еСlJИ
обе
перемtllllы
е
(
в
данном
случае
пер
мен
ные
расстшIНИЯ
ТОЧЮI
от
центра
и
нпtl~НИЯ
величины
в
данной
точке)
или
увеличиваются
WIИ
уменьшаются,
то
к
суммирующей
перемснной
прибав.ляс
'
I'CЯ
единица
.
Если
одна
переменнан
возрастаег,
а
другая
уменьшается,
то
су
ммирующая
ш:ременная
(аккумулятор)
уменьшается
на
1.
В
конце
pacL,eT
oB
аККУМУШIТОР
делится
на
<IИСЛО
таких
сравнений
П(Il-1)/2,
чтобы
в
итоге
получился
результирующий
коэффициент
корреляции
Т,
находящийся
в
интервале
от
-1
до
+ 1.
Таким
образом,
Д1Ы
Дё.1нного
пр.{мера
,
ест.
значения
(Il
стоянно
возрастают
npl1
ув
е
личении
расстояния
01'
Р,
то
мы
ПОЛу<IИМ
лоложителы
ый
коэффицие
н
т
Т,
а
в
случае
уменьшеtшя
зна
'
Iений
-
отрицательный.
Величина
Т
может
бы
ь
использована
как
о
{енщик
ДJ1Я
О
.
Поскольку
зна<
lсние
Q
может
находится
в
интервале
от
О
до
),
то
снязь
между
ЭТ
И~fИ
параметрами
можно
выразить
с
ледующим
уравнением
1
+ ,
....
,,-
-
..
-
р
+
--
+
Plll
8.-.
ЮI
дВ
хмерного
про
гранства
медиана
lIе
ВС
та
У
"
Ш
lfii
lще
ll
Щ
ИК
AJНI
u
JlИЧIIIIЫ
Р
.
5

Q = 0.5
(l
-T), (8.1)
где
высокие
значения
Т
вы
з
ывают
ни
зкие
з
н
аче
ния
Q,
от
ражая
ту
ситуацию,
при
которой
Т
находите}}
на
впздине
сред
и
ни
з
ких
значений
величин
.
До
сих
пор
р
ас
сматривалея
случай,
к
огда
точки
да
нных
лежали
внугри
огр:ннrченной
окрестности
Р
,
но
ее
размер
не
бьUl
опр
ед
елен
,
а
все
точки
наблюдений
имели
одинаковые
веса
.
Мо
ж
но
принять
Ilроизвольное
.
решение
о
включении
lU1И
ИСlU1ючении
и
з
рассматриваемого
множества
наблюд
е
ний
,
расположенных
н
а
гр
а
ниц
е
выбранной
окрестности
.
На
практике
,
чтобы
и
бежать
нереальных
"скачков"
оценив
аем
ых
з
наtl
е
ний
при
п
е
реход
е
от
одной
точки к
следующей,
лучше
все
же
исполь
з
ошпь
некоторый
набор правил
для
определения
окрестности.
В
самом
деле
,
эта
идея идет
следом
за
концеrщи
й
интервала
ра€стояния
('пшgе'),
который
широко
испо
льзуетс
я
при
по
ст
роении
и
моделировании
вариограмм
в
классич
ес
кой
геостатистике:
с
увеличением
расстояния
от
Р
в
е
роя
т
ность
наб
л
ю
ден
ий
,
лежащих
внутри
окрестности
Р
уменьшаетсн,
а за
пределами
Оllр
едел
енного
расстоsIНИЯ
от
Р
можно
с
уверенностью
полагать,
что
встретившиесн
здесь
наблюдения
лежат
'
за
границами
окрестности
Р
.
В
непараметрической
геостатис
т
ик
е
отсутствуют
предположения
об
однородности
рассматриваемой
структуры
или
о
том
,
что
п
олученная
вариограмма
остается
постоянной
для
люб
ы
х
рас
1'0яниЙ.
Таким
образом,
график
вариограммы
не
мож
ет
б
ыть
использован
для
оценки
вероятности
принадлежности
к
окрестности
Р.
Оставшаяся
альтернатива
использовать
не
который
стандарт
н
ый
алгоритм,
основанный
чисто
на
расстонниях
и
отсутс
т
вии
к.,ких
-1'
о
особе
нны
х
структурных
связей.
Простейшан
подходящая
функция
метод
обратных
рас
ст
ояний,
имеет
достоинство
в
том
,
что
она
уже
с
успехом
широко
применяется
в
интерполяционны
х
расчет
ах
.
еперь
б
лижайшая
точка
к
Р
будет
находится
обизательно
внутри
окрестности
Р
,
можно
следовательно
выполнить
любую
ее
оценку
и
ей
должен
быть
присвоен
вес
= 1.
Однако,
ее
ра
ссто
ян
ие не
мож
ет
быть
выражено
в
ело
ре
дстве
нным
и
з
мер
нием
от
точки
Р
.
Оно,
'
o)(~
ого,
должно
определятьс
я
по
щии
вычи
с
ляющ
ей
взвешенное
а с
стонние
:
L--_-:--::-
__
.
_____
___
-._
Ри
с.8
.
6.
ОцениваНIIС
районов
раслро
р
а
н
е
lll1Я
1S(
~Л
Н
(
III11
,
больших
ИЛII
М
IIЫfШ
Х
,[
С
М
Р

и.(~
=:
(dПlin
/d)n, (8.2)
где
11
-
по
азатель
степени,
используемый
Д/lЯ
расстояний
в
расчеТах,
должен
быть
равным
ДНЯ
двух
или
трехмерных
пространств
по
крайней
мере
2.
Однако,
это
не
только
проблема
взвешивания
.
Рас
мотрим
эффект
группы
близко
расположенных
наблюдений
по
сравнению
с
одним
изолированным
наблюдением
на
таком
же
расстоянии
от
Р.
Очевидно
,
что
информация,
вносимая
I'Рynпой
в
оценку
значения
в
точке
Р
,
не
будет
слишком
большой
по
сравнению
с
информацией
от
одного
изолированного
наблюдения.
В
этом
случае
необходимо
вводИ1Ъ
в
расчет
весовых
коэффициентов
специальные
факторы
,
компенсирующие
воздействие
группы
данных
на
величиНу
оценки
.
В
кригинге
факторы
взвешивания
рас
считываются
с
учетом
расстояний
,
и
эффект
кластеров
(групп
данных)
не
учитывается
,
поэтому
отдельный
расчет
повторнетсн
Для
каЖдОЙ
оцениваемой
точки.
Однако,
кластеризация
это
чисто
геометрическая
пробл
ема
стратегии
опробования,
и
она
должна
Уl.tитываТI;>СЯ
при
расчет
е
множества
весов
один
раз
(при
проектировамии
разведочной
сети)
.
Каждая
точка
данных
должна
быть
отдельно
проверена,
и
"кластерный
вес",
присвоенный
ей,
зависит
от
степени
кластеризации
данных
в ее
окрестности.
Степень
кластеризации
может
бьrrь
определена
более
или
менее
точно,
как
максимальное
положительное
отклонение
от
однородного
распределения
точек
данных
в
н-мерном
пространстве
вокруг
оцениваемой
точки.
Хорошо
известный
непараметрический
тест
lVIЯ
отклонения
от
идеального
распределения
-
это
тест
Колмогорова-Смирнова.
Принцил
этой
проверки
заКЛЮ'lаеТСJ!
в
сравнении
2-х
кумулят
.
ивных
кривых
частот,
одна
из
которых
может
быть
1.
идеальной"
кривой,
авторан
-
кривой
реального
множества
наблюдений.
Чтобы
получить
идеartЬНУЮ
кривую
ДIlЯ
данного
случая,
предположим
окрестность
с
центром
в
данной
точке
и
N
наблюдений,
неравномерно
размещенных
в
данной
окрестности.
На
нулевом
расстоянии
обе
кумулятивн
ые
кривые
будyl
'
совпадать
со
значением
l/N
.
Идеальная
кривая
(длн
КУМУnЯТИВНОl
'
О
числа
точек
данных
,
лежащих
ближе
к
Р
,
вычерченных
на
гр
а
фике
в за
висимости
от
расстояния)
будет
D
данном
случае
прямой
линией
-
ДIlЯ
одномерных
данных,
параболой
-
ДJlЯ
2-х
мерн
ых
и
кубической
кривой
-
для
3
-
х
мерных.
Выч
е
рченная
кривая
ре
альных
наблюдений
будет
выглядеть
зигзагообразной
лицией,
пересекающей
идеальную
кривую.
Если
реальная
кривая
расположена
выше
идеальной,
то
предполагается
некоторое
количество
кластеров,
Степень
кластеризации
может
быть
выражена
максимальным
положит~льным
отклонением
между
указанными
кривыми.
Однако,
в
связи
с
тем,
что
степень
кластеризации
для
больших
расстояний
между
точками
данных
не
.
очень
важна
,
то
максимальное
отношение
2-х
кривых
чаще
используется
на
практике.
Таким
образом,
кластерный
ве
определнетси
п\)
ф
о
рмуле
w(c) = 1 / sup(d/d*), (8.3)
где
веШIЧИ/Ш
w(
c)
мож
l'
принимать
значения
в
интервале
от
О
до
1.
16
7
Таким
образом,
при
интерполяции
каждой
т
'IK"
каждому
наблюдению
ilриписыв
ается
фак
т
ор
взвешивания,
которЫ
I
Яlll1яется
про"зводныM
от
w(d)
и
w(c);
вме
то
единствен
'
ного
КОЭФФlщиенТа
корреляции
Кедалла,
используемого
ДJlЯ
оценки
квантиля
Q,
раСС'lитывается
взвешенный
вариант
со
взвеШНВUlI
,
н
е
м
каждого
сравненм,
НВJlЯющимся
ПРО:ИЗDОДНЫМ
01
'
весон
двух
срщшив
емых
наБЛЮД~tш}1.
8.4.
Пример:
Моделирование
же
еЗОРУДlШfО
месторождени
.
Я.
Одним
из
наиболее
ра~ПРОСТРctненных
напраш
ений
ИСН
льзования
I'е
ост ати
стики
являетсн
оценка
рудных
за
пасов
,
Эти
з
адачи
требуют
использования
возможно
более
эффективных
методов,
дающих
наиболее
точные
и
несмtщенные
оценки,
т
.
к.
ДJUl
большинства
месторождений
ошибки
в
предсказании
качества
руды
ведуг
к
серьезным
экономическим
проблемам
в
будущем
.
Последние
20
лет
по'!
и
повсеместно
для
решения
оценочных
задач
применялись
(с
переменным
успехом)
геостатистические
методы
Криге
и
Матерона.
Они
в
то
же
время
бьUlИ
удобным
эталоном
для
сравнения
с
новыми
полвляющимися
методами
·
оц
нки
запасов
,
В
идеальных
обстонтелъствах
геостатистика
дает
оп
тималь
ные
и
несмещенныt
оценки,
И
,Кл
арк
(1979)
ИJUtюстрировала
исполь
зов
вие
условного
линейного
кригинг
а
на
модели
железорудного
ме
торождения,
представляющего
собой
квадрат
со
стороной
400
м,
опробованный
50
неравномерно
размещенными
образцами.
Район
был
поде
ен
на
64
блока
размерами
50
х
50
м,
ДJU1
каждого
из
кот
рых
линейным
блочным
кригингом
была
рассчитана
оценка
содержания.
После
того
оценки
сраВНИВaJ1НСЬ
с
реальным..и
средними
содержаниями
в
блоках.
Для
этих
же
исходных
данных
была
использована
н
парам
е
трическая
гео,,:татистика,
а
полученные
результаты
сравнены
с
о
енками
критинга
в
Таблице
8.2,
Оказалось,
что
эффект
1ВН ст
ь
неl1арам
е
ричес
их
методов
вполне
сравнима
с
кригингом
по
ВСJlИ'll1Н
ошибки
И
смещ~ния
.
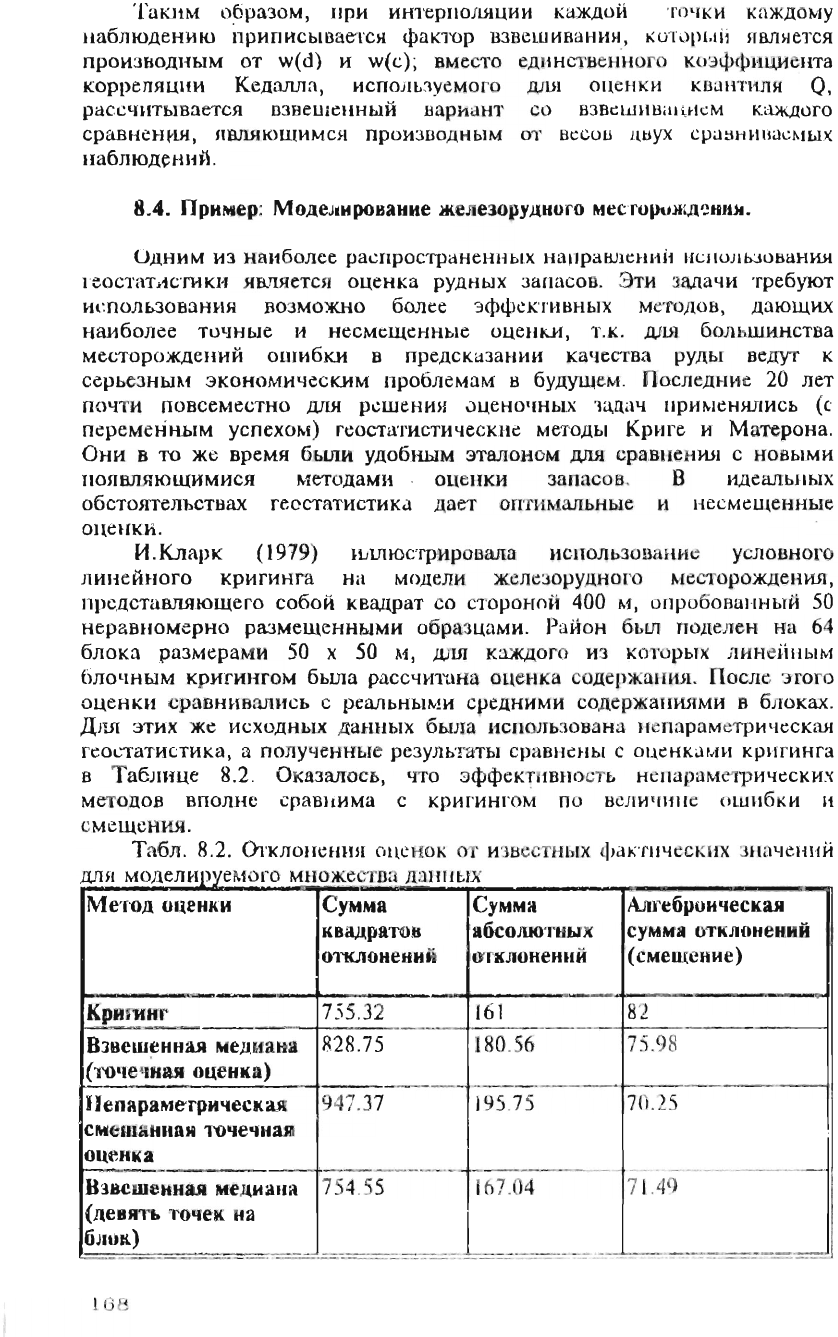
Табл
.
8.2.
О1
'
клонеюlЯ
оценок
о
изве
.
ных
фактичеСКIfХ
з
начений
ДЛН
модеЛИj)уt;~ОI
'
О
множе
СТ
D
а
даНIIЫХ
Метод
оценки
Сумма Сумма
Алгеброическая
квадратов
аБСОJOOl
'
НЫХ
сумма
отклонений
отклонении
отклоненttЙ
(смещение)
-
КРИJ'ИНf'
755.
32
161
82
_ _
о
Взвешенная
медиана
828.75
180
.56
75
,98
(точе
чная
оценка)
-
Непараметрическая
9 7.
37
195
.
75
7()
,
25
СМС
uаНШUI
точечная
OlteHKa
--
--
----
-
--
_._-----
-
-----
.....
Взвешенна.и
медиана
754
. 5
16
7.
04
71
4f)
(цевить
точек
на
БJIOК)
-
.=
_ _.""
-'=='-
.--=-"=::-
,:"o-_
"=-=:::
·.
~
.~==
-
==
- -
-
-

ГеОC'F.IТИСТИ'iескне
метОДЫ,
оперирующие
с
любы
ми
раСllр
!
щелен
иями
,
рассмотренные
в
этом
разделе,
вполне
соизмеримы
с
кригингом
в
качестве
оценивания
,
что
видно
из
приведенного
выше
маленького
при
мера.
Более
того,
их
надежность
дает
возможность
получить
достове
рную
оценку
там,
где
Теория
ПРО(..Jpанственных
Пер менных
не
может
дать
гарантию
успеха.
Зги
ре
з
ультаты
получены,
когда
развитие
так.нх
не
Л
<1ра
метрических
методов
находится
лишь
на
начальной
стадии
.
Можно
ожидать
значит
еJlЬНОГО
угочнения
И
улучшения
данных
методов,
особ~нно
процедуры
взвешивания
по
расстояниям.
РазВИ'I1Iе
непарамеТРИ'Jес
ких
э
квивалентов
вариограмм
для
структурного
анализа
МШI
ет
дать
некоторый
положительный
эффект,
но
эти
методы
в
ероя
но
дадут
отдачу
8
случаях,
когда
имеется
некоторая
местная
стац
ионарность
И,
следовательно,
определенная
упорядоченная
структу ра
анализируемых
данных.
Возможн
о,
что
подход
"последовательных
разностей"
(successive
dift'erence approacll),
который
подцерживает
Де
Вийс,
будет
хорошо
совмещаТЬС1
1
с
непараметрическими
методами
оценки
с
построением
"д
евиограмм"
или
"мадограмм",
р&ссчитываемых
по
абсолютным
зна
ч
ения
м
разлИ'JИЙ
(разностей),
в
то
время,
как
вариограr-
.f
ма
использ
ует
квадраты
разностей.
Хотя
построить
новую
теоретИ'JеСk'YfO
О
СНОВУ
для
такого
метода
достаточно
сложно,
но
подход
посл
едова
ельных
.
р
аз
ностей,
похожий
на
непараметрические
о
ц
еночные
методы
,
нес
омненно
легt.Jе
в
понимании
и
использовании
ге
о
лога
ми
и
горннками.
НепарамеТ
РИ'l
еСКi1Я
или
независимая
от
типа
распред~ления
теХНОЛОГИ
Я
(когда
она
будет
достаточно
развита)
будет
в
общем
работать
быстрее
(и
естественно
-
дешевле)
чем
сопоставимы
е
пара
метрИ'Jеские
ме
о
ды
с
гораздо
меньшим
количеством
различных
ограниче
ний
.
Однако,
положение
непарамеТРИ'Jеской
геостатистики
в
данный
момент
похоже
на положение,
которое
з
аним
ала
п
ара
метрическая
геОС1
'
атистика
в
конце
1950
годов
и
начале
1960
-х,
когда
до
тупные методы
были
примитивны
и
ограничены
по
сравнению
с
д
ругими
,
которые
сегодня
уже
праКТИ'Jески
не
применя
ю
тсн
и
з-
з
;}
их
явной
отсталости.
8.5.
Ра.18ИТl
lе
неш_раметрических
меТОДОI
На
н
аш
югляд
выше
бьиа
приведена
достаточная
информация
ДЛЯ
КОМIJСтентно
о
программиста,
чтобы
он
смо
г
составить
с
вои
собстн
нные
алго
ритмы
ДJIЯ
непараметрических
прогр
ам
м
,
используs
JРИ
необход
имости
стандартные
статистические
процедуры,
такие
к
а
к
вы
чи
сле
ни
е
медианы,
корреляционных
коэффициентов
Кендалла
'
И
т.п
.
Полный
набо
р
программ
непаР.1.~етрических
методов
содержится
в
со
о
ветствующем
модуле
интегрированной
системы
Датам
а
йн
,
а
т
ексты
этих
прогр~мм,
н~\Писанные
на
Фортране
,
могуг
быть
получены
от
авторов.
Э
I
'
И
МС;ТО
Д
Ы
испытывались
и
сравни
вались
с
линейной
геос
ТИСТl1КОЙ
'Нl
нескольких
достаточно
простых
прим
е
р
ах,
в
р
·ЗУJlЬТ
Т
ч
е
г)
ПОJl)
Г
1I
е
ны
вп
ли
со
поставимые
результа
ты
.
Они
также
примеllflJIН\.
'
IН
оце
н
ки
апасов
месторождения
серебра
lJ
ИЛИ
,
де
1 9
