Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

70
Ответ: два корня.
2) у = 8х
3
– 3х
4
– 7 = 0
1. Область определения R:
2. y′ = 24x
2
– 12x
3
3. y′ = 0; 12x
2
(2 – x) = 0, x = 0, x = 2
X
(-∞;0)
0 (0;2) 2
(2;+∞)
y’ + 0 + 0 -
Y -7 9
max
Ответ: два корня.
№ 935
()
3
3
1
4
−
−
=
x
x
y ;
1) Область определения х ≠ 1;
2)
()
(
)
(
)
() ()
=
−
+−−
=
−
−−−−
=
4
323
6
3
23
2
1
12333
1
41313
'
x
xxx
x
xxxx
y
(
)
()
4
2
1
43
−
−
x
x
3) y′ = 0,
(
)
()
0
1
43
4
2
=
−
−
x
x
, x = ±2;
4)
X
(-∞;-2)
-2 (-2;1) (3;2) 2
(2;+∞)
y’ - 0 + + 0 -
Y
9
4
4
min max
5) y = 0, x
3
= 4,
3
4=x , x = 0, y = 4;
6)
()
()
()
()
3
2
3
2
3
3
3
1
333
1
1
3331
1
4
−
−−
+=
−
−−+−
=
−
−
x
xx
x
xxx
x
x
,
x → ∞ y → 1. Т.к. (0,9) > 0 y(1,1) < 0, то слева от х = 0 у → +∞,
а справа растет от -∞
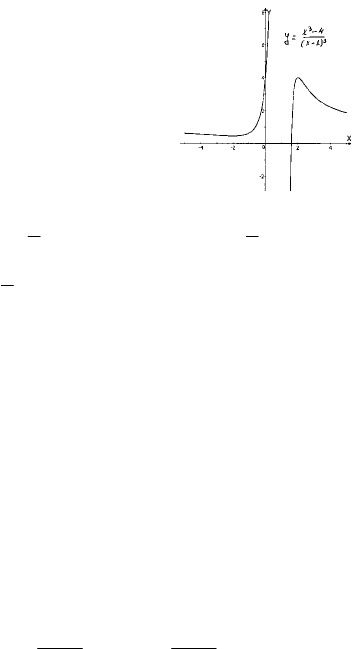
71
7) Рассмотрим график;
9
4
<c
имеем один корень;
9
4
=c
два корня;
1
9
4
<< c
три корня; с = 1 два корня; 41
<
<
c три корня;
с = 4 два корня; с > 4 один корень.
§ 52 Наибольшее и наименьшее значения функции
№ 936
а) х
экстр
= -3; 0 у
наиб
= 2 у
наим
= -3
б) х
экстр
= 0 у
наиб
= 3 у
наим
= -3
в) х
экстр
= -2; 2 у
наиб
= 3 у
наим
= -3
г) х
экстр
= -2; 1 у
наиб
= 4 у
наим
= -2
№ 937
1) у = 2х
3
+ 3х
2
– 36х на [-4; 3];
1. у(-4) = 2 ⋅ (-64) + 3 ⋅ 16 – 36 ⋅ (-4) = 64,
y(3) = 2 ⋅ 27 + 3 ⋅ 9 – 36 ⋅ 3 = -27;
2. y′ = 6x
2
+ 6x – 36, y′ = 0; x
2
+ x – 6 = 0, D = 1 + 24 = 25,
2
2
51
1
=
+−
=x
,
3
2
51
2
−=
−−
=x
;
3. 2 ∈ [-4; 3], -3 ∈ [-4; 3], y(-3) = 2 ⋅ (-27) + 3 ⋅ 9 – 36(-3) = 81,
y(2) = 2 ⋅ 8 + 3 ⋅ 4 – 36 ⋅ 2 = -44,
[]
() ( )
813 max
3;4
=−=
−
yxy ,
(
)
(
)
442 min
]3;4[
−==
−
yxy ;
2) на [-2; 1];
а) f(-2) = 2 ⋅(-8) + 3 ⋅ 4 – 36(-2) = 68, f(1) = 2 + 3 – 36 = -31;
б) 2 ∉ [-2; 1], -3 ∉ [-2; 1], значит
[]
(
)
68max
1;2
=
−
xf ,
[]
(
)
31min
1;2
−=
−
xf .
№ 938
1) f(x) = x
4
– 8x
2
+ 5 на [-3; 2];
1. f(-3) = 81 – 8 ⋅ 9 + 5 = 14, f(2) = 16 – 8 ⋅ 4 + 5 = -11;
2. f’(x) = 4x
3
– 16x, f’(x) = 0; 4x(x
2
– 4) = 0, x = 0, x = ±2;
3. D ∈ [-3; 2], -2 ∈ [-3; 2], 2 ∈ [-3; 2], f(0) = 5, f(-2) = -11, f(2) = -11,
72
[]
()
143max
2;3
=−
−
f ,
[]
(
)
(
)
(
)
1122min
2;3
−
=
−
=
=
−
ffxf ;
2)
()
x
xxf
1
+= ,
⎥
⎦
⎤
⎢
⎣
⎡
−−
2
1
;2;
1.
()
2
5
2
1
22 −=−−=−f
,
2
5
2
2
1
2
1
−=−−=
⎟
⎠
⎞
⎜
⎝
⎛
−f ;
2.
()
2
1
1'
x
xf −=
, f’(x) = 0, x
2
– 1 = 0, x = ±1;
3.
⎥
⎦
⎤
⎢
⎣
⎡
−−∉
⎥
⎦
⎤
⎢
⎣
⎡
−−∈−
2
1
;21
2
1
;21, f(-1) = -1 – 1 = -2,
() ( )
21max
2
1
;2
−
=
−=
⎥
⎦
⎤
⎢
⎣
⎡
−−
fxf ,
() ( )
2
1
2
2
1
2min
2
1
;2
−=
⎟
⎠
⎞
⎜
⎝
⎛
−=−=
⎥
⎦
⎤
⎢
⎣
⎡
−−
ffxf
;
3) f(x) = sinx + cosx
⎥
⎦
⎤
⎢
⎣
⎡
π
π
2
3
;;
1. f(π) = sinπ + cosπ = 0 – 1 = -1,
101
2
3
cos
2
3
sin
2
3
−=+−=
π
+
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
f ;
2. f’(x) = cosx – sinx, f’(x) = 0; cosx – sinx = 0, cosx ≠ 0,
1 – tgx = 0, tgx = 1,
Znnx ∈π+
π
= ,
4
;
3.
⎟
⎠
⎞
⎢
⎣
⎡
π
π∈
π
2
3
;
4
5
,
2
2
2
2
2
4
5
cos
4
5
sin
4
5
−=−−=
π
+
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
f ,
() ()
1
2
3
max
2
3
;
−=
⎟
⎠
⎞
⎜
⎝
⎛
π
=π=
⎥
⎦
⎤
⎢
⎣
⎡
π
π
ffxf
,
()
2
4
5
min
2
3
;
−=
⎟
⎠
⎞
⎜
⎝
⎛
π
=
⎥
⎦
⎤
⎢
⎣
⎡
π
π
fxf
.
№ 939
1)
()
2
2
16
x
xxf +=
, х > 0;
1. Область определения: х > 0,
()
3
32
2'
x
xxf −=
,
f’(x) = 0;
0
322
3
4
=
−
x
x
, 2(x
4
– 16) = 0, x = ±2;
2 ∈ (0; +∞) -2 ∉ (0;+∞), x = 2 – точка минимума,
()
8
4
16
42 =+=f ;
–
+
2
х

73
2)
()
2
2
x
x
xf −=
, x < 0. Область определения x < 0;
1.
()
x
x
xf 2
2
'
2
−−= , f’(x) = 0,
(
)
0
x
x12
2
3
=
+−
, x
3
= -1, x = -1,
-1 ∈ (-∞; 0)
+
–
-1
х
()
31
1
2
1 −=−−=−f
, x = -1 – точка максимума,
()
() ( )
31max
0;
−
=−=
∞−
fxf .
№ 940
Пусть одно число х, тогда второе (50 – х). Надо найти наименьшее зна-
чение суммы их кубов, т.е.: f(x) = x
3
+ (50 – x)
3
,
f’(x) = 3x
2
– 3(50 – x)
2
= 3x
2
– 7500 + 300x – 3x
2
= 300x – 7500, f’(x) = 0,
300x – 7500 = 0 ⇒ x = 25,
–
+
25
х
x = 25 – точка минимума, х = 25; (50 – х) = 25, 50 = 25 + 25.
№ 941
Пусть одно число х, тогда второе
⎟
⎠
⎞
⎜
⎝
⎛
x
625
, но числа эти такие, что сумма
их квадратов наименьшая
()
2
2
625
⎟
⎠
⎞
⎜
⎝
⎛
+=
x
xxf , x < 0,
()
3
2
6252
2'
x
xxf
⋅
−=
,
()
,0
6252
2;0'
3
2
=
⋅
−=
x
xxf
2х
4
– 2 ⋅ 625
2
=0, x = ±25, x = 25 ∈ (0; + ∞), x = -25 ∉ (0; +∞),
–
+
25
х
x = 25 – точка минимума, значит х = 25,
25
625
=
x
.
Ответ: 625 = 25 ⋅ 25
№ 942
Пусть стороны прямоугольника равны a и b, тогда
p = 2(a + b). Положим, а = х, тогда x > 0
x
p
a
p
b −=−=
22
.
а
b

74
Площадь этого прямоугольника находим как:
()
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=⋅== x
p
xbaxfS
2
– найдем max этой функции.
()
x
p
xx
p
xf 2
22
' −=−−=
, f’(x) = 0;
4
0
2
4 p
x
xp
==
−
,
+
–
4
p
х
точка
4
p
x = – точка max, значит, прямоугольник имеет стороны
442
4
ppp
b
p
a =−==
— это квадрат.
№ 943
Пусть стороны прямоугольника равны a и b.
S = 9 = a ⋅ b.
Пусть а = х, тогда
x
b
9
=
,
() ( )
⎟
⎠
⎞
⎜
⎝
⎛
+=+==
x
xbaxfp
9
22 x > 0.
Найдем минимум этой функции
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
2
9
12'
x
xf
,
f′(x) = 0;
(
)
0
9
2
2
2
=
−
x
x
, x = ±3,
–
+
3
3 ∈ (0; +∞) -3 ∉ (0; +∞)
х = 3 – точка min; a = 3,
3
3
9
==b .
Ответ: Это квадрат со стороной 3.
№ 944
1) f(x) = lnx – x,
⎥
⎦
⎤
⎢
⎣
⎡
3;
2
1
, х > 0; 1.
0
2
1
2
1
ln
2
1
<−=
⎟
⎠
⎞
⎜
⎝
⎛
f , f(3) = ln3 – 3 < 0;
2.
()
1
1
' −=
x
xf
, f′(x) = 0;
0
1
=
−
x
x
, x = 1; 3.
⎥
⎦
⎤
⎢
⎣
⎡
∈ 3;
2
1
1, f(1) = ln1 –1=-1.
Выясним, что больше. Допустим,
()
3
2
1
ff >
⎟
⎠
⎞
⎜
⎝
⎛
33ln
2
1
2
1
ln −>−
,
2
5
3ln
2
1
ln −>−
,
2
5
2
5
1
6
1
ln
6
1
ln
e
e >⇒>
−
е
5/2
> 6 – что верно
75
Допустим f(3) < f(1), т.е. ln3 – 3 > -1, ln3 > 2, ln3 > lne
2
,
3 > e
2
– не верно, значит f(1) > f(3).
Допустим
()
1
2
1
ff >
⎟
⎠
⎞
⎜
⎝
⎛
, т.е.
1
2
1
2
1
ln −>−
,
2
1
ln
2
1
ln
−
> e ,
e
1
2
1
> ,
2>e
, е > 4 – не верно, значит
()
⎟
⎠
⎞
⎜
⎝
⎛
>
2
1
1 ff .
Итак,
()
(
)
11max
3;
2
1
−
=
=
⎥
⎦
⎤
⎢
⎣
⎡
fxf ,
(
)
(
)
33ln3min
3;
2
1
−
=
=
⎥
⎦
⎤
⎢
⎣
⎡
fxf ;
2) f(x) = x + e
-x
, [-1; 2];
1. f(-1) = -1 + e = e – 1 < 2, 2 < e < 3, 1 < e – 1 < 2,
()
2
1
22
2
>+=
e
f ;
2. f′(x) = 1 – e
-x
, f′(x) = 0; 1 – e
-x
= 0, e
-x
= 1 = e
0
, x = 0, f(0) = 0 + e
0
= 1,
[]
() ()
2
2;1
1
22max
e
fxf +==
−
,
[]
(
)
(
)
10min
2;1
=
=
−
fxf ;
f
(0)
f
(-1)
f
(2)
1 2
3) f(x) = 2cos x – cos2x, [0; π];
1. f(0) = 2cos0 – cos0 = 2 – 1 = 1, f(π) = 2cosπ - cos2π = -2 – 1 = -3;
2. f′(x) = -2sin x + 2sin2x, f′(x) = 0; -2sin x(1 – 2cos x) = 0,
sinx = 0, x = πn, n ∈ Z,
Znnxx ∈π+
π
±=+= ,2
3
2
1
cos
;
3. 0 ∈ [0; π], π ∈ [0; π],
[]
π∈
π
;0
3
,
2
3
2
1
1
3
2
cos
3
cos2
3
+=++=
π
−
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
f
,
[]
()
2
3
3
max
;0
=
⎟
⎠
⎞
⎜
⎝
⎛
π
=
π
fxf ,
[]
(
)
(
)
3min
;0
−
=
π
=
π
fxf .
№ 945
1)
()
xxxxf −= 3 , x > 0;
1.
()
x
x
xf ⋅−=
2
3
2
3
',
f′(x) = 0;
0
1
0
1
2
3
=
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
x
x
x
x
, x = 1
+
–
0 1
x = 1 – точка max, f(1) = 3 – 1 = 2;
76
2.
()
xxxxf 23 −=
, x > 0,
(
)
xxf 33' −=
,
f′(x) = 0;
(
)
013 =− x , 1=x , x = 1, x = 1, точка max.
3. 1 ∈ (0; +∞), f(1) = 3 – 2 = 1.
1
+
–
№ 946
1) f(x) = e
3x
– 3x на (-1; 1), f′(x) = 3e
3x
– 3,
f′(x) = 0, 3(e
3x
– 1) = 0, e
3x
= 1 – e
0
, x = 0, x = 0 – точка min, 0 ∈ (-1; 1),
f(0) = e
3⋅0
– 3 ⋅ 3 = 1;
0
–
+
2)
()
x
x
xf ln
1
+=
на (0; 2),
()
x
x
xf
11
'
2
+−=
, f′(x) = 0,
0
1
2
=
−
x
x
,
x = 1, х = 1 – точка min, 1 ∈ (0;2),
()
11ln
1
1
1 =+=f .
1
–
+
№ 947
1)
()
4
5 xxxf −= на (0; 5),
()
(
)
()
(
)
()
()
4
3
4
3
4
3
4
54
520
54
54
54
1
5'
x
x
x
xx
x
x
xxf
−
−
=
−
−−
=
−
−⋅
+−=
,
f′(x) = 0,
()
0
54
520
4
3
=
−
−
x
x
, x = 4, x = 4 – точка max, 4 ∈ (0; 5),
()
44544
4
=−⋅=f
;
4
+
–
2)
()
3
4 xxxf −= , (0; 4),
()
(
)
()
()
3
2
3
2
3
43
412
43
1
4'
x
x
x
x
xxf
−
−
=
−
−⋅
+−=
,
f′(x) = 0,
()
0
43
412
3
2
=
−
−
x
x
, x = 3, х = 3 – точка max, 3 ∈ (0; 4),
()
33433
3
=−⋅=f ;
3
+
–
x
77
3)
() ( )
3
2
1 xxxf −= , (0; 1),
()
()
(
)
(
)
() () ()
3
2
4
3
2
4
2
3
2
4
2
13
32
13
32
13
1121
'
xx
x
xx
xx
xx
xxx
xf
−
−
=
−
−
=
−
−⋅+−
=
f′(x) = 0,
()
0
13
32
3
2
4
=
−
−
xx
x
,
3
2
=x
,
3
2
=x
– точка max,
()
1;0
3
2
∈
,
3
4
3
1
9
4
3
2
3
3
=⋅=
⎟
⎠
⎞
⎜
⎝
⎛
f ;
3
+
–
x
4)
()
3
2
54 +−= xxxf , (-1; 5),
()
(
)
()
2
2
543
421
'
+−
−⋅
=
xx
x
xf ,
f′ (x) = 0;
()
0
543
42
3
2
2
=
+−
−
xx
x
, x = 2, x = 2 – точка min., 2 ∈ (-1; 5),
()
15842
3
=+−=f
.
2
–
+
x
№ 948
Пусть мы вырежем квадраты со стороной х, тогда высота и есть х. За-
пишем в таком случае объем
f(x) = V = (a – 2x)(a – 2x) ⋅ x = (a – 2x)
2
⋅ x = a
2
x – 4a
2
x + 4x
3
f′(x) = a
2
– 8ax + 12x
2
;
f′(x) = 0: 12x
2
– 8ax + a
2
= 0, D = 16a
2
– 12a
2
= 4a
2
,
212
24
1
aaa
x =
+
=
,
612
24
2
aaa
x =
−
=
,
()()
0
22
=⋅−−=
⎟
⎠
⎞
⎜
⎝
⎛
a
aaaa
a
f ,
27
2
69
4
6336
3
2
aa
a
aa
a
a
a
a
f =⋅=⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
,
()
27
2
6
max
3
aa
fxf =
⎟
⎠
⎞
⎜
⎝
⎛
= .
Ответ: высота коробки должна быть
6
a
.

78
№ 949
Пусть BK = х, тогда высота треугольника BD=a + x.
Найдем основание АС. Треугольники АВС и PQB – по-
добны с коэффициентом
x
ax +
, значит
x
ax
PQ
AC +
= ,
(
)
(
)
x
aax
x
PQax
AC
⋅+
=
⋅+
= .
Площадь:
()
()
(
)
x
aax
xa
x
aax
BDAC
22
1
2
1
2
⋅+
=+⋅
+
=⋅ ,
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++⋅=
2
22
1
2
'2
2
'
x
a
ax
a
ax
a
xf ,
f′(x) = 0;
0
2
2
22
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
x
ax
a
, x = ±a, x > 0, x = a,
()
()
2
2
2
2
a
a
aaa
af =
⋅+
= .
Ответ: наименьшая площадь при ВК = a.
№ 950
у = 3 – х
2
– график этой функции симметричен относительно оу, значит,
вершины прямоугольника будут иметь координаты
В = (-х, у); А = (-х, 0); С = (х, у); D = (x, 0).
Основание прямоугольника равно 2х (х>0) и высота у, значит, площадь:
f(x) = S = 2x ⋅ y = 2x ⋅ (3 – x
2
), x ∈ (0; 3),
f′(x) = 2(3 – x
2
) + 2x ⋅ (-2x) = 6 – 2x
2
– 4x
2
= 6(1 – x
2
),
f′(x) = 0; 6(1 – x
2
) = 0, x = ±1, 1 ∈ (0; 3) -1 ∉ (0; 3),
f(1) = 2 ⋅ 1(3 – 12) = 2 ⋅ 2 = 4.
Ответ: наибольшая площадь прямоугольника равноа 4.
№ 951
Пусть это точка В с координатами (х, х
2
).
Тогда расстояние до точки А:
()()
ρ=−+−
22
BA
yyxx или
() ( )
=+−++−=
⎟
⎠
⎞
⎜
⎝
⎛
−+−==ρ
4
1
44
2
1
2
242
2
2
2
xxxxxxxf
4
17
4
4
+−= xx ,
()
(
)
4
17
42
441
'
4
3
+−
−⋅
=
xx
x
xf
,
К
Р Q
C
A
D
B
79
f'(x) = 0;
0
4
17
42
44
4
3
=
+−
−
xx
x
,
1
–
+
x
x
3
= 1, x = 1, х = 1 – точка минимума, у = 1
2
= 1.
Ответ: (1; 1) — ближайшая к точке А.
№ 952
Пусть а — ширина доски, ϕ – угол,
2
0
π
<ϕ≤
.
Тогда площадь поперечного сечения желоба:
() () ( )
ϕ⋅+
⎟
⎠
⎞
⎜
⎝
⎛
ϕϕ⋅=ϕ cossincos
2
1
2 aaaaS ,
()
⎟
⎠
⎞
⎜
⎝
⎛
ϕ+ϕ=ϕ cos2sin
2
1
2
aS .
Найдем максимум этой функции:
S′(x) =
⎟
⎠
⎞
⎜
⎝
⎛
ϕ−ϕ⋅⋅ cos2sin2
2
1
2
a ,
S′ = 0 ⇒ cos2ϕ – sinϕ = 0 ⇒ 1 – 2sin
2
ϕ – sinϕ = 0.
Обозначим sinϕ = t;
2t
2
+ t – 1 = 0; t
1,2
=
(
)
22
12411
⋅
−⋅−±−
; t
1
= –1; t
2
=
2
1
.
при t = –1: sinϕ = –1 ⇒ ϕ =
π
2
3
— посторонний корень.
при t =
2
1
: sinϕ =
2
1
⇒ ϕ =
6
π
, и угол наклона боковых досок к осно-
ванию : π=
π
+
π
3
2
62
.
Ответ:
π
3
2
.
§ 53 Выпуклость графика функции, точки перегиба
№ 953
1) f
′′
(x) = (x
2
cosx)′′ = (2x cosx – x
2
sinx)′ = (2x cosx)′ – (x
2
sinx)′ =
= 2cos x – 2x sin x – 2xsinx – x
2
cosx = cosx(2 – x
2
) – 4x sin x;
2) f
′′
(x) = (x
3
sinx)′′ = (3x
2
sinx + x
3
cosx)′ = 3(x
2
sinx)′ + (x
3
cosx)′ =
= 6x sin x + 3x
2
cosx + 3x
2
cosx – x
3
sinx = sinx(6x – x
3
) + 6x
2
cosx;
