Кадеев А.А. Домашняя работа по алгебре за 11 класс

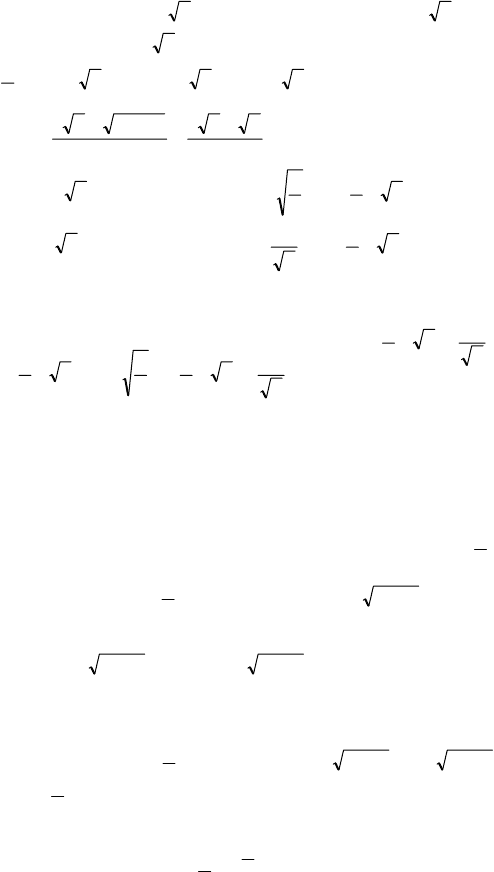
280

x

2

+4xy–4+4x–x

2

+8y–4xy–4y

2

=0; – 4+4x+8y–4y

2

=0; – 1 + x + 2y – y

2

= 0;

x = (y – 1)

2

, подставим в первое уравнение исходной системы:

8 ·

()

2

1

2

−− y

+

2

y

= 23 ; 8 ·

yyy 2123

2

−−+−

+

2

y

= 23;

2

·

2

y−

+

2

y

= 23;

2

y

= a > 0;

23

4

2

=+ a

a

; 4 + a

2

= 23 a; a

2

– 23 a + 4 = 0;

2

223

2

161823

2/1

±

=

−±

=a

.

1) a

1

= 22, тогда

2

y

2= 2

3/2

;

2

3

y ±=

;

16

2

3

x +±=

.

2) a

2

= 2, тогда

2

y

2= 2

1/2

;

2

1

y ±= ;

12

2

1

x +±=

;

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

±±

⎟

⎠

⎞

⎜

⎝

⎛

±+±

>

>−−

>+

2

1

;2

2

3

,

2

3

;16

2

3

0x

0y2x2

0y4x

. Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

±±

2

1

;2

2

3

.

№ 1434

()

⎩

⎨

⎧

=−−+

=−−

0a5y2ax

0xlog23ylog

2

93

; y > 3; x > 0;

⎩

⎨

⎧

=−−−++

+=⇒=−

0a56x2aax2x

3xyx3y

22

.

Хотя бы одно решение D ≥ 0.

x

2

+ (2a – 2)x + a

2

– 5a – 6 = 0;

D/4=(

a–1)

2

–a

2

+5a+6=a

2

–2a+1–a

2

+5a+6=3a+7; 3a + 7 ≥ 0; a ≥

3

7

−

;

D = 0,

x = 1 – a = 1 +

3

7

> 0; D > 0, x

1

= 1 – a +

7a3 +

> 0.

См. в конце.

x

2

= 1 – a – 7a3 + > 0; 1 – a = 7a3 + , 1 – a > 0, a < 1

1 – 2

a + a

2

> 3a + 7, a

2

– 5a – 6 > 0;

⎪

⎩

⎪

⎨

⎧

−<

<

>−<

3

7

1

6и1

a

aa

⇒

3

7

−

< a < –1, x

1

=1–a + 7a3 + > 0; 7a3 + > 1 – a

1)

a – 1 < 0; a < 1,

⎪

⎩

⎪

⎨

⎧

−>

<

3

7

a

1a

,

3

7

−

< a < 1

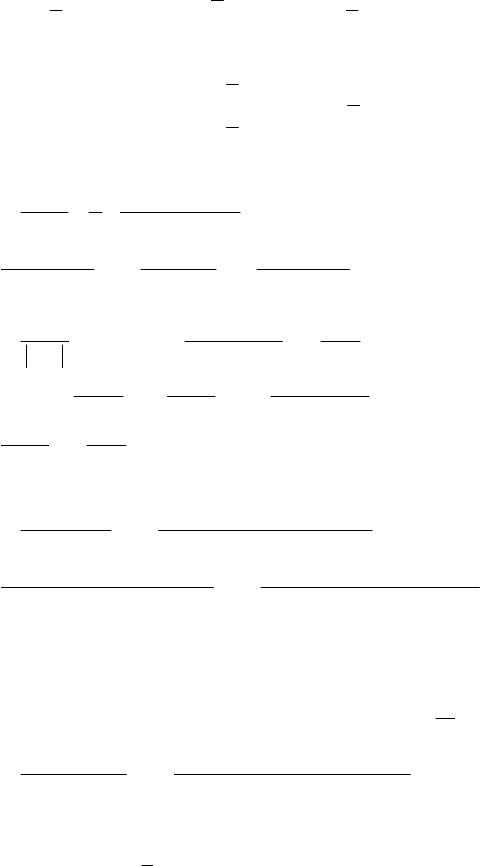
281

2)

a – 1 ≥ 0; a ≥ 1; 3a + 7 > a

2

– 2a + 1; a

2

– 5a – 6 < 0;

⎪

⎩

⎪

⎨

⎧

≥

−<

<<−

1a

3

7

a

6a1

⇒ 1 ≥

a < 6;

⎢

⎣

⎡

<<

≥<−

6a1

1a

3

7

;

3

7

−

< a < 6,

одновременно

x

1

и x

2

> 0,

⎪

⎩

⎪

⎨

⎧

−<<−

<<−

1a

3

7

6a

3

7

⇒

3

7

−

< a < –1.

№ 1435

1)

x

1

x4

3x2

>

−

;

()

0

x4x

x4x3x2

2

>

−

+−−

;

()

0

x4x

4x2x2

2

>

−

−−

;

()

;0

4xx

2xx

2

<

−

−−

(

)

(

)

()

0

4xx

2x1x

<

−

−+

.

Ответ: х ∈ (–1; 0) U (2; 4).

2)

1

1x

5x2

≥

+

; 1.

х > –1;

()

0

1x

4x

;0

1x

1x5x2

≥

+

≥

+

−−+

; х ∈ (–1; +∞).

2.

х < –1;

1

1x

5x2

≥

−−

+

;

1

1x

5x2

−≤

+

;

0

1x

1x5x2

≤

+

+++

;

0

1x

2x

;0

1x

6x3

≤

+

≤

+

; х ∈ [–2; -1). Ответ: х ∈ [–2; -1) U (–1; +∞).

№ 1436

1) a

xx

≤

+−

124

348

2

; 0

124

24348

2

22

≤

+−

−+−+−

xx

aaxaxxx

;

0

124

32448

2

32

≤

+−

−++−−

xx

aaxxaxx

;

(

)

(

)

(

)

0

124

32448

2

≤

+−

−+−−−

xx

aaxax

;

4

x

2

–2x+1<0 при любых х; найдем значения а, для которых х

2

(8–4а)–x(4–2a)+

+(3 –

a) ≤ 0 при любых х: 8–4a<0, т.е. а>2 и D = (4 – 2a)

2

– 4(3 – a)(8 – 4а) ≤ 0;

16 – 16

a + 4a

2

– 4(24 – 12a – 8a + 4a

2

) = –12a

2

+ 64a – 80;

12

a

2

–64a+80≥0; 6a

2

–32a+40≥0; 3a

2

–16a+20≥0; a ∈ (–∞; 2] U [10/3; +∞).

Таким образом

х

2

(8 – 4а) – x(4 – 2a) + (3 – a) ≤ 0 при а ≥

3

10

.

2)

a

xx

≥

+−

16129

843

2

; 0

16129

16129843

2

22

≥

+−

−+−+−

xx

aaxaxxx

;

9

x

2

– 16x + 16 > 0 при любых х; найдем значения а, для которых 3х

2

– 9аx

+12a

x – 4x + 8 – 16a ≥ 0 независимо от х. х

2

(3–9а)+x(12a – 4) + (8 – 16a) ≥ 0:

3 – 9

а ≥ 0, т.е.

3

1

≤

a

, D = (6a – 2)

2

– (8 – 16a)(3 – 9а) ≤ 0;

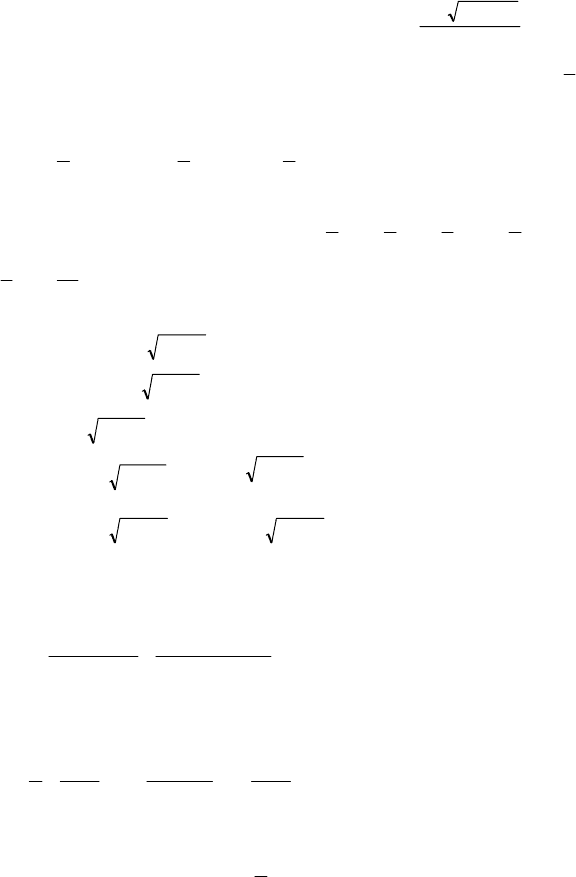
282

36a

2

– 48a + 4 – (24 – 72a – 48a + 144a

2

) = –108a

2

+ 72a – 20;

–108a

2

+ 72a – 20 ≤ 0; 27a

2

– 18a + 5 ≥ 0 (1);

27

135819

2/1

−±

=a ;

D < 0 ⇒ неравенство (1) выполнено при любом а, таким образом

3

1

≤a

.

№ 1437

1)

06565

5

2

5

2

;1

5

2

22

⎟

⎠

⎞

⎜

⎝

⎛

<

⎟

⎠

⎞

⎜

⎝

⎛

<

⎟

⎠

⎞

⎜

⎝

⎛

+−+− xxxx

x

2

– 5x + 6 > 0; (x – 2)(x – 3) > 0; x ∈ (–∞; 2) U (3; +∞).

2) 5

x

– 3

x+1

> 2(5

x

– 3

x+1

); 5

x

– 3 · 3

x

>

xx

3

9

2

5

2

⋅−⋅

;

03

9

7

25

5

3

>⋅−⋅

xx

;

03

9

25

5

3

>⋅−⋅

xx

; 27 · 5

x

– 125 · 3

x

> 0; 3

3

·5

x

–5

3

·3

x

> 0; 3

3

· 5

x

> 5

3

· 3

x

; x > 3.

№ 1438

1) log

1/2

(1 + x – 4x

2

− ) ≤ 0

⎪

⎩

⎪

⎨

⎧

>−−+

≤

⎟

⎠

⎞

⎜

⎝

⎛

−−+

)2(041

)1(1log41log

2

2/1

2

2/1

xx

(1) 1 + x –

4

2

−x ≥ 0;

⎪

⎩

⎪

⎨

⎧

≥−≥

−≥

04,0

4

2

xx

; x

2

≥ x

2

– 4;

⎩

⎨

⎧

≥

−≥

2

40

x

; x ≥ 2.

(2) 1 + x –

4x

2

− > 0; 1 + x > 4x

2

− ;

⎪

⎩

⎪

⎨

⎧

−>++

≥−

>+

421

04

01

22

2

xxx

x

;

(

][

)

⎪

⎩

⎪

⎨

⎧

−>

≥∞+∪−∞−∈

−>

5,2

.2;;22;

1

x

xx

x

⎩

⎨

⎧

≥

2

x

; x ≥ 2.

2)

() ()

0

x23log4

1

x23log

1

55

<

−−

−

;

()

⎪

⎩

⎪

⎨

⎧

≠−−

≠−

>−

0x23log4

0x23log

0x23

5

– область определения; log

5

(3 – 2x) = a

0

4

11

<

−

aa

;

0

4

2

;0

4

<

−

<

−

−−

a

aa

;

2<log

5

(3–2x)<4; log

5

2

<log

5

(3–2x)<log

5

4

; 25 < 3 – 2x < 4

4

; 11 < –x < 311;

()

⎪

⎩

⎪

⎨

⎧

≠−−

≠−

>−

−>>−

023log4

023log

023

31111

5

x

xx

;

⎪

⎩

⎪

⎨

⎧

−≠

≠

<

−<<−

311

1

2

3

11311

x

; –311 < x < –11.

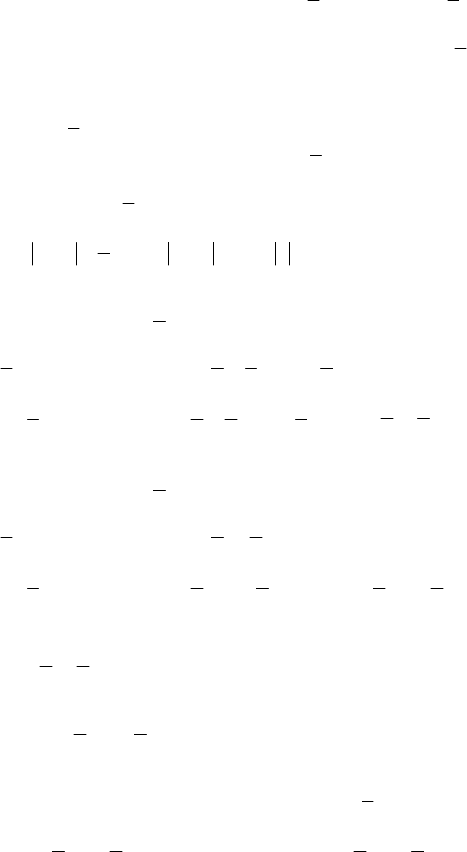
283

№ 1439

1) log

|2x + 1|

x

2

≥ 2; log

|2x + 1|

x

2

≥ 1) log

|2x + 1|

2

1. |2x + 1| > 1, т.е. x ∈ (–∞; –1) U (0; +∞); x

2

≥ (2x + 1)

2

x

2

≥ 4x

2

+ 4x + 1; 3x

2

+ 4x + 1 ≤ 0; (x + 1)(x +

3

1

) ≤ 0. x ∈ [–1; –

3

1

].

2. |2x + 1| < 1, т.е. x ∈ (–1; 0); x

2

≤ 4x

2

+ 4x + 1; x ∈ (–∞; –1) U (–

3

1

; +∞);

()()

()

⎢

⎣

⎡

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

∞+−∪−∞−∈

−∈

⎪

⎩

⎪

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

−−∈

∞+∪−∞−∈

;

3

1

1;

0;1

3

1

;1

;01;

x

. Ответ: x ∈ [–

3

1

; 0].

2)

2

1

1x3log

2

x

<+

;

xlog1x3log

22

xx

<+

1.

x

2

> 1, x ∈ (–∞; –1) U (1; +∞); |3x + 1| < |x|

a)

x ≥ 0, 3x + 1 < x, x < –

2

1

; x ∈ ∅

б) –

3

1

≤ x < 0, 3x + 1 < –x, x < –

4

1

;–

3

1

≤ x < –

4

1

в)

x < –

3

1

, –3

x – 1 < –x, x > –

2

1

;–

2

1

<

x < –

3

1

.

x ∈ .

4

1

;

2

1

⎟

⎠

⎞

⎜

⎝

⎛

−−

2.

x

2

< 1, x ∈ (–1; 1); |3x + 1| > |x|

a)

x ≥ 0, 3x + 1 > x, x > –

2

1

; x ≥ 0;

б) –

3

1

≤ x < 0, 3x + 1 > –x, x > –

4

1

; –

4

1

<

x < 0;

в)

x < –

3

1

, –3x – 1 > –x, x < –

2

1

; x < –

2

1

; x ∈ .;

4

1

U

2

1

;

⎟

⎠

⎞

⎜

⎝

⎛

∞+−

⎟

⎠

⎞

⎜

⎝

⎛

−∞−

Решением исходного неравенства является система:

()()

()

⎢

⎣

⎡

⎪

⎩

⎪

⎨

⎧

−∈

⎟

⎠

⎞

⎜

⎝

⎛

∞+−∪

⎟

⎠

⎞

⎜

⎝

⎛

−∞−∈

⎪

⎩

⎪

⎨

⎧

∞+∪−∞−∈

⎟

⎠

⎞

⎜

⎝

⎛

−−∈

1;1x

;

4

1

2

1

;x

;11;x

4

1

;

2

1

x

.

Кроме того по определению логарифма

x ≠ 0, x ≠ –

3

1

, тогда

x ∈

()

.10;U0;

4

1

U

2

1

;1

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

Ответ: x ∈

()

.10;U0;

4

1

U

2

1

;1

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

284

№ 1440

0

3x

4x3xx37

2

<

−

−++−

;

⎩

⎨

⎧

≠−

≥−+

03x

04x3x

2

– область определения;

0

3x

3x4x3xx37

2

<

−

−+−++−

; 0

3x

4x3xx24

2

<

−

−++−

;

⎢

⎣

⎡

⎪

⎩

⎪

⎨

⎧

<−

>−++−

⎪

⎩

⎪

⎨

⎧

>−

<−++−

03x

04x3xx24

03x

04x3xx24

2

1)

⎪

⎩

⎪

⎨

⎧

>−

<−++−

03x

04x3xx24

2

;

03x

04x2

4x24x3x

2

>−

−<−+

;

⎪

⎩

⎪

⎨

⎧

>

+−<−+

3x

2x

16x16x44x3x

22

; 3x

2

– 19x + 20 > 0;

x ∈

()

∞+

⎟

⎠

⎞

⎜

⎝

⎛

∞− 5;U

3

4

;;

()

⎪

⎩

⎪

⎨

⎧

>

∞+∪

⎟

⎠

⎞

⎜

⎝

⎛

∞−∈

3x

;5

3

4

;x

; x ∈ (5; +∞).

2)

⎪

⎩

⎪

⎨

⎧

<−

>−++−

03x

04x3xx24

2

;

⎪

⎩

⎪

⎨

⎧

<

−>−+

3x

4x24x3x

2

;

()

⎪

⎩

⎪

⎨

⎧

<

⎢

⎣

⎡

∞−∈

⎟

⎠

⎞

⎜

⎝

⎛

∈

3x

2;x

5;

3

4

x

; x ∈ (–∞; 3);

()

⎪

⎩

⎪

⎨

⎧

⎢

⎣

⎡

∞−∈

∞+∈

≠−

≥−+

3;x

;5x

03x

04x3x

2

;

(

]

[

)

()

[

)

⎪

⎩

⎪

⎨

⎧

∞+∪∞−∈

≠−

∞+∪−∞−∈

;53;x

03x

;14;x

.

Ответ: (–∞; –4] U [1; 3) U (5; +∞).

№ 1441

log

1/2

(x

2

+ ax + 1) < 1, x < 0; log

1/2

(x

2

+ ax + 1) < log

1/2

1/2;

x

2

+ ax + 1 > ½; x

2

+ ax + 1/2 > 0; 2x

2

+ 2ax + 1 > 0.

Для любых

х < 0 неравенство выполняется в двух случаях:

1) D =

a

2

– 2 < 0, т.е. a ∈

(

)

2;2−

.

2)

⎩

⎨

⎧

>

0x

2

1

т.е.

⎪

⎩

⎪

⎨

⎧

>−−−

>−+−

02aa

2

285

a)

2a

2

− > a, ;

0a

a2a

02a

22

2

⎪

⎩

⎪

⎨

⎧

⎢

⎣

⎡

<

>−

≥−

(

]

[

)

⎪

⎩

⎪

⎨

⎧

⎢

⎣

⎡

<

∅∈

∞+∪−∞−∈

0a

a

;22;a

a ∈ (–∞; 2− ]

б) –

2a

2

− > a, 2a

2

− < –a

(

] [

)

⎪

⎩

⎪

⎨

⎧

<−

>−

∞+∪−∞−∈

22

a2a

0a

;22;a

a ∈ (–∞; 2− ]

Таким образом, ответом на вопрос задачи является система

()

(

]

⎢

⎣

⎡

−∞−∈

−∈

2;a

2;2a

. Ответ: a ∈ (–∞; 2− ].

№ 1442

y=(x–1)

2

, 0≤x≤1; y=x

2

–2x+1; y=f′(x

0

)(x – x

0

)+f(x

0

);

y=(2x

0

–2)(x–x

0

)+

2

0

x –2x

0

+1; y = 2xx

0

– 2

2

0

x – 2х + 2x

0

+

2

0

x – 2х

0

+ 1;

y = 2xx

0

– 2х – 2

2

0

x + 1; y = x(2x

0

– 2) + (1 – 2

2

0

x ).

Точки пересечения касательной с осями:

x = 0, y = 1 – 2

2

0

x

y = 0,

2x2

1x2

x

0

2

0

−

= , тогда площадь треугольника,

()

(

)

()

0

2

0

2

0

2

0

x222

1x2

1

x21

2x2

1x2

2

1

xS

−

=

−

⋅

−

⋅=

;

()

(

)

()

0

2

0

2

0

2

0

x222

1x2

1

x21

2x2

1x2

2

1

xS

−

=

−

⋅

−

⋅=

;

()

() () ()

()

=

−

−+⋅−

=

′

⎟

⎠

⎞

⎜

⎝

⎛

−

=

′

2

0

2

00

2

0

2

0

x44

1x24x41x22

x44

1x2

xS

(

)

(

)

()

2

0

2

0

4

00

2

0

x44

1x4x44x42x4

−

−−+⋅−

= .

Минимум данной функции

S′(x

0

) в точке х

0

=

3

1

, у

0

=

9

4

. Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

9

4

;

3

1

.

№ 1443

Уравнение касательной в точке х

0

выглядит у′(х

0

)(х – х

0

) + у(х

0

). Она

прямая. Из этого следует, что для любой касательной, проходящей через

центр

у(х

0

) – у′(х

0

)х

0

= 0, (у′(х

0

)(х – х

0

) + у(х

0

) = kx + b)

у(х

0

) = 8x3x2

0

2

0

+− , у′(х

0

) = 4х

0

– 3 ⇒

2

0

x2 – 8 = 0 ⇒ х

0

= ±2

Легко проверить, что в этих точках касательная проходит через центр.

286

№ 1444

у = x

2

+ 2x – 3, y = kx + 1. Ошибка в условии.

№ 1445

y = x

2

+ px + q, y = 2x – 3; x = 1.

Найдем точки пересечения:

у = 1 · 2 – 3 = –1, тогда для p и q справедливо

–1 = 1 +

p + q, т.е. p + q = –2 (использовали уравнение y = x

2

+ px + q)

Вершины параболы имеют координаты

⎟

⎠

⎞

⎜

⎝

⎛

+

−

⎟

⎠

⎞

⎜

⎝

⎛

−

− q

2

p

2

p

,

2

p

2

, т.е.

расстояние до оси О

х

равно

p

q

pp

q

pp

y −−−=+−=+−

⎟

⎠

⎞

⎜

⎝

⎛

−

= 2

42422

2222

2

0

2

2p

1

2

p

y

0

−−

=−−=

′

, очевидно р = –2 точка минимума, тогда q = 0, а

кратчайшее расстояние равно 1.

№ 1446

y = 4x – x

2

,

⎟

⎠

⎞

⎜

⎝

⎛

6;

2

5

M; y = f′(x

0

)(x – x

0

) + f(x

0

);

y′=4–2x, тогда уравнение касательной имеет вид: y=(4–2x

0

)(x–x

0

)+4x

0

–

2

0

x ;

y = 4x – 4x

0

– 2xx

0

+ 2

2

0

x + 4x

0

–

2

0

x ; y =

2

0

x – 2xx

0

+ 4x.

Известно, что эта касательная проходит через точку М, тогда

6 =

2

0

x – 5x

0

+ 10;

2

0

x – 5x

0

+ 4 = 0;

x

0

= 1, x

0

= 4, т.е. получим уравнения касательных y=1 + 2x и y = 16 – 4x;

Касательные пересекаются в точке с абсциссой

6

15

, тогда искомая площадь

()

(

)

(

)

∫∫∫

=−−−++=

4

6/15

4

1

2

6/15

1

441621 dxxxdxxdxxS

() ()

25,2

3

1

2216

4

1

32

4

6/15

2

6/15

1

2

=

⎟

⎠

⎞

⎜

⎝

⎛

−−−++= xxxxxx

№ 1447

y = 6cos

2

x + 6sinx – 2

Перепишем данную функцию в виде

y = 6(1 – sin

2

x) + 6sinx – 2, y = –

6sin

2

x + 6sinx + 4, положим y′ = –12sinxcosx + 6cosx = 0, 6cosx(1 – 2sinx) = 0

cos

x = 0, Znnx ∈π+

π

= ,

2

; sinx =

2

1

,

()

Znnx

n

∈π+

π

−= ,

6

1;

Znnx ∈π+

π

= ,2

6

и

Znnx ∈π+

π

= ,2

6

5

– точки max ⇒

Ответ:

()

Znnx

n

∈π+

π

−= ,

6

1

.

287

№ 1448

y = x

2

+ (a + 4)x + 2a + 3, x ∈ [0; 2]; y

min

= –4; y′ = 2x + a + 4;

y′ = 0, 2x + a + 4 = 0,

2

4

−−

=

a

x

.

Ветви параболы направлены вверх, т.е.

2

4−−

=

a

x

– точка минимума.

Рассмотрим три случая. 1) вершина параболы лежит правее

x = 2, тогда

минимальное на отрезке [0; 2] значение она принимает в точке

x = 2, т.е.

()

⎪

⎩

⎪

⎨

⎧

++⋅++=−

≥

−−

322444

2

4

aa

a

– решений нет

2) вершина параболы лежит внутри отрезка [0; 2]:

()( )

⎪

⎩

⎪

⎨

⎧

++

−−+

+

⎟

⎠

⎞

⎜

⎝

⎛

−−

=−

<

−−

<

32

2

44

2

4

2

4

0

2

a

aaa

a

– решений нет

3) вершина параболы лежит левее

х = 0;

⎪

⎩

⎪

⎨

⎧

+=−

≤

−−

324

0

2

4

a

a = –3,5.

№ 1449

y = 4x

2

– 4ax + a

2

– 2a + 2< x ∈ [0; 2]; y

min

= 3. Ветви параболы направ-

лены вверх.

y′ = 8x – 4a; y′ = 0; 8x – 4a = 0, x =

2

a

1)

⎪

⎩

⎪

⎨

⎧

+−+−=

≥

228163

2

aaa

a

a = 5 +

10

2)

⎪

⎩

⎪

⎨

⎧

+−+⋅⋅−⋅=

<<

22

2

4

43

2

0

2

aa

a

– решений нет

3)

⎪

⎩

⎪

⎨

⎧

+−=

≤

223

0

2

aa

a

a = 1 – 2

Рассмотрели три случая: в первом – вершина лежит правее х = 2, т.е.

минимальное значение на [0; 2] данная функция принимает в точке х = 2; во

втором – вершина лежит внутри [0; 2], т.е. минимальное значение – в точке

х =

2

a

; в третьем случае – вершина лежит левее точки х = 0, т.е. минималь-

ное значение на отрезке [0; 2] данная функция принимает в точке х = 0.

Ответ: a = 5 +

10 ; a = 1 – 2.

288

№ 1450

y = 4x

2

+ 8ax – 9, y = 4ax

2

+ 8x + a – 2; y = –5.

Найдем ординаты вершин парабол:

y

1

= 4(–a)

2

+ 8a(–a) – 9 = –4a

2

– 9;

2

4

2

84

2

1

8

1

4

2

−+−=−+−=−+

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

= a

a

aa

a

aa

ay

.

Возможны два случая:

1)

⎪

⎩

⎪

⎨

⎧

−>−+−

−>−−

52a

a

4

59a4

2

;

⎪

⎩

⎪

⎨

⎧

>++−

−<

03a

a

4

4a4

2

;

⎪

⎩

⎪

⎨

⎧

>++−

−<

03a

a

4

1a

2

– чего не может

быть ни при каких

а

2)

⎪

⎩

⎪

⎨

⎧

−<−+−

−<−−

52a

a

4

59a4

2

;

⎪

⎩

⎪

⎨

⎧

<++−

−>

03a

a

4

4a4

2

;

⎪

⎩

⎪

⎨

⎧

<++−

−>

03a

a

4

1a

2

– это при любых а

Рассмотрим два случая

1) a > 0,

3a

a

4

++−

< 0; –4 + a

2

+ 3a < 0; a

2

+ 3a – 4 < 0

a ∈ (–4; 1) и a > 0, следовательно, 0 < a < 1; a < 0.

2) –4 +

a

2

+ 3a > 0; a

2

+ 3a – 4 > 0; a < –4 и a > 1, но a < 0; a < –4.

Ответ:

a < –4, 0 < a < 1.

№ 1451

xx

y

24

cos3sin2

sincos2

+

=

;

(

)

(

)

()

−

+

′

+

=

′

2

24

2424

cos3sin2

cos3sin2sincos2

xx

xxxx

y

()( )

()

=

+

′

++

−

2

24

2424

cos3sin2

cos3sin2sincos2

xx

xxxx

(

)

(

)

()

−

+

+⋅+⋅−

=

2

24

243

cos3sin2

cos3sin2cossin2sincos8

xx

xxxxxx

(

)

(

)

()

2

24

324

cos3sin2

sincos6cossin8sincos2

xx

xxxxxx

+

⋅−+

−

Знаменатель дробей не влияет на исследование функции

у, т.к. не может

обращаться в 0 и не может быть отрицательным.

(

)

(

)

xxxxxx

243

cos3sin2cossin2sincos8 +⋅+⋅− –

–

(

)

(

)

xxxxxx sincos6cossin8sincos2

324

⋅−⋅+ =

= sin

x · cosx(2 – 8cos

2

x)(2sin

4

x + 3cos

2

x) – cosx·sinx(8sin

2

x–6)(2cos

4

x+3sin

2

x) =

= sin2

x(1 – 4cos

2

x)(2sin

4

x + 3cos

2

x) – sin2x(4sin

2

x – 3) (2sin

4

x + 3cos

2

x) =

=sin2

x(2sin

4

x+3cos

2

x–8sin

4

x·cos

2

x–12cos

4

x–8sin

2

x·cos

4

x–4sin

4

x+6cos

4

x+3sin

2

x) =

=sin2

x(–2sin

4

x–6cos

4

x+3–8sin

2

x·cos

4

x–8sin

4

x·cos

2

x)=sin2x(–2sin

4

x–6cos

4

x+3 –

– 8sin

2

x · cos

2

x(cos

2

x + sin

2

x))

2

=sin2x(–2sin

4

x – 6cos

4

x + 3 – 2sin

2

x)

Отсюда получаем максимальное значение

3

2

и минимальное значение

15

7

.

Кадеев А.А. Домашняя работа по алгебре за 11 класс

Подождите немного. Документ загружается.