Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.


220
() ()
()
423223
32,22'
−+−=−+−=
−==
xxy
ff
72 −= xy
— уравнение касательной в точке х
0
= 2.
№ 1283
232
2
++−= xxy
1) график функции – парабола, ветви на-
правлены вниз; вершина с координатами
,
8
1
3,
4
3
00
== yx
точки пересечения с 0у: (0;2);
с 0х: (2;0), (- ½ ; 0) у(х) < 0 при x > 2 и x < - ½
2) y′ – 4x + 3 < 0 при
4
3
>x
, следовательно на [1;2] функция убывает
3) наибольшее значение функция принимает в точке
4
3
=x
4)
23 += xy ,
23232
2
+<++− xxx
,
02
2
<− x
,
0
2
>x , следовательно при всех 0
≠
x ;
5)
;23
2
23 ;3 ++−== xxy
;
2
1
,1 ;013
2
2 ===+− xxxx
()
4 ,11' +=−= -xyy - уравнение касательной в х = 1
5,2 ;1
2
1
' +==
⎟
⎠
⎞
⎜
⎝
⎛
xyy - уравнение касательной в
2
1
=
x
№ 1284
1) y = x
2
и y = x + 6, x
2
= x + 6,
x
2
– x – 6 = 0 D = 1 + 24 – решение есть, след. пересекаются.
2)
x
y
3
=
и
()
14
+
= xy ,
034 ,43 ;14
3
22
=−++=+= xxxxx
x
,
D = 1 + 48 – решение есть, след. пересекаются.
3)
x
yxy
1
и
8
1
2
== ,
x
x
1
8
1
2
= , 8
3
=x , 2
=
x , след. пересекаются.
4)
x
yxy
1
и 12 =−=
,
x
x
1
12 =−
,
81D 012
2
+==−− xx – решение есть, след. пересекаются.
№ 1285
1)
xx
y
−
+= 22
,
() ()
xy
xx
xy =+
−
=− 22 – функция четная
2)
xx
y
−
−= 33
,
() ()
xy
xx
xy −=−
−
=− 33 – функция нечетная
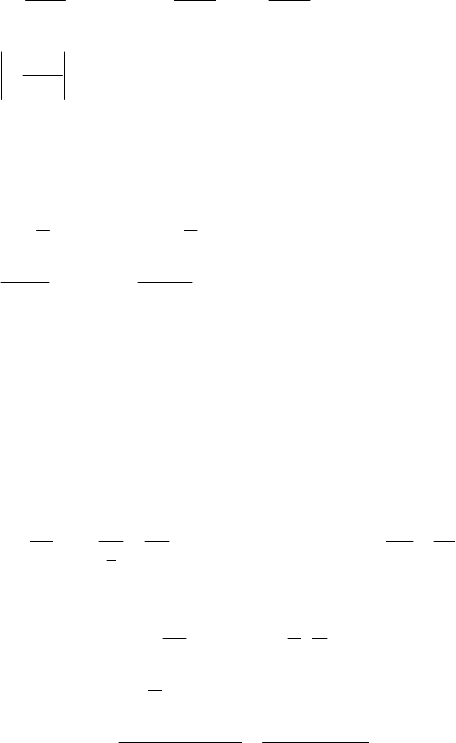
221
3)
x
x
y
−
+
=
3
3
ln
,
() ()
xy
x
x
x
x
xy
−=
−
+
−=
+
−
=−
3
3
ln
3
3
ln – функция не-
четная
4)
() ()
xyxy
x
x
y
=−
−
+
= ;
5
5
ln – функция четная
№ 1286
1) 12
2
−= xy ,
()
(
)
(
)
xyxxy =−−=− 12
2
– функция четная
2)
3
xxy −= ,
()
(
)
xyxxxy −+−=− =
3
– функция нечетная
3)
x
xy
1
5
−= ,
() ()
xy
x
xxy =+−=−
1
5
– функция нечетная
4)
()
x
x
y
sin
=
,
() ()
xy
x
x
xy =
−
=−
sin
– функция четная
№ 1287
1) xxy sin= ,
()
(
)
(
)
xyxxxy
=
−
−
=
− sin – функция четная
2)
xxy cos
2
= ,
()
(
)
(
)
xyxxxy =−=− cos
2
– функция четная
3)
xxy sin+= ,
(
)
(
)
xyxxxy
−
=
−
−
=
−
sin – функция нечетная
4)
x
x
y cos+= ,
(
)
xxxy cos
+
−
=
−
— функция не является четной и
не является нечетной.
№ 1288
1)
2
3
cos
x
y
=
3
42
2
3
π
=
π
=T 2) xy 6,0sin2
=
π=
π
=
3
10
6,0
2
T
№ 1289
1).
3
2
;23;3cos
π
=π== TTxy
; 2). π=π== 10;2
5
;
5
sin T
Tx
y ;
3).
5
;5;5
π
=π== TTxtgy
;
4).
)1(cos
cos
)1(cossin
cos
sincossin
;sin +=
+
=
+
=+= xtgx
x
xx
x
xxx
ytgxxy
;
Наименьший период для sin x 2π, для tgx 2π тоже являются периодом.
Следовательно для у = sinx + 69x Т=2π.
№ 1290
1) 54
24
−+−= xxy ,
(
)
(
)
xyxxxy =−+−=− 54
24
– функция четная
2)
xxy 4
3
−= ,
()
(
)
xyxxxy −=+−=− 4
3
– функция нечетная
222
№ 1291
4
2
−+= bxaxy ,
(
)
(
)
04 ,01 == yy ,
;
44160
40
⎩
⎨
⎧
−+=
−+=
ba
ba
;
041616
4
⎩
⎨
⎧
=−+
−=
aa
ab
⎩
⎨
⎧
=+
−=
01212
4
a
ab
⎩
⎨
⎧
−=
=
1
5
a
b
45
2
−+−= bxy .
Наибольшее значение функция принимает в точке
;
2
5
=x
25,2
2
5
=
⎟
⎠
⎞
⎜
⎝
⎛
y
№ 1292
1)
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
π
−=−=−=
3
2sin22cos
2
3
2sin
2
1
22cos32sin xxxxxy
2)
(
)
=+−=+= xxxxxxy
22222
cossin4sincos22sin2cos2
(
(
)
(
=−⋅+−−= xxxx
2222
sin1sin2sinsin12
(
)
xxxx
2422
sin42sin2sin2sin212 −=−+−=
0sin1
2
≥≥ x , 2
max
=y , 2
min
−=y . (Опечатка в ответе задачника).
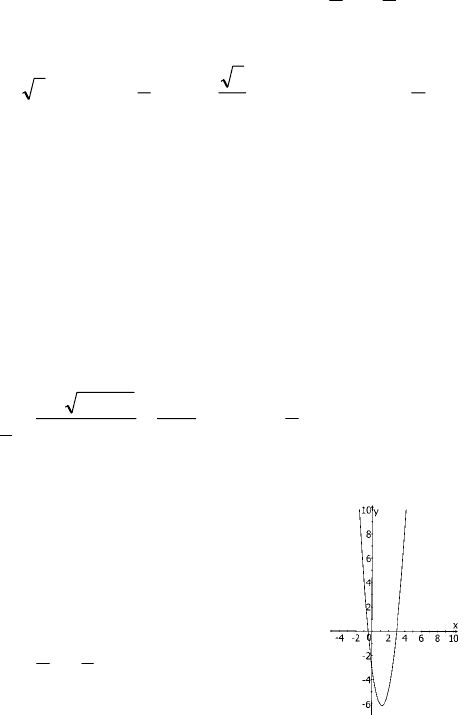
№ 1293
1)
65
2
2 +−= xxy
, с осью 0y: х = 0, у = 6 ⇒ (0, 6),
с осью 0х пересечений нет, т.к. D < 0;
2) 25
2
2 +−= xxy , c осью 0у: х = 0, у = 2 ⇒ (0, 2)
с осью 0х:
4
35
4
16255
2
1
±
=
−±
=x
, (2, 0) и
⎟
⎠
⎞
⎜
⎝
⎛
0,
2
1
.
№ 1294
cbxaxy ++=
2
,
(
)
(
)
(
)
30 ,03 ,152
−
=
=
=
−
yyy
⎪
⎩
⎪
⎨
⎧
⎪
⎩
⎪
⎨
⎧
⎪
⎩
⎪
⎨
⎧
=
=
=
+=
=+
=
=−
++=
+−=
-3c
-5b
2a
;
3-2-6a4a15
b13a-
-3c
;
3
300
2415
c
cba
cba
352
2
−−= xxy — график функции — парабола с
вершиной в точке
⎟
⎠
⎞
⎜
⎝
⎛
−
8
1
6,
4
5
, ветви которой направле-
ны вверх.
223
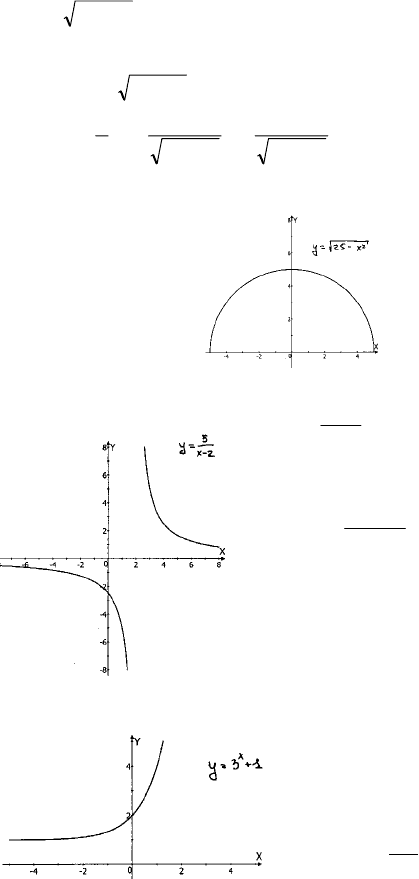
№ 1295
2
25 xy −= ,
1)
()
(
)
(
)
[
]
5;5 ;055 ,025
2
−=≥+−≥− yDxxx ;
2)
() ()
xyxxy =−=−
2
25
— четная;
3)
22
2525
1
2
2
1
'
x
x
x
xy
−
−=
−
⋅⋅−=
, у′ = 0 при х = 0;
4) т.к. функция четная, то график функции симметричен относительно
0у. Функция возрастает на [-5,0] и убывает на [0,5].
№ 1296
2
5
−
=
x
y
1)
(
)
(
)
(
)
+
∞
−
∞
=
;22; UyD ; 2) Ни чет-
ная, ни нечетная, непериодическая
3)
()
2
2
5
'
−
−
=
x
y
, 0'
≠
y , следователь-
но стационарных точек нет.
4) 0у: х = 0, у = -1,25, 0х: пересечений
нет;
5) y′ < 0 при 2
≠
x , следовательно
функция убывает.
№ 1297
1) 13 +=
x
y
а)
(
)
(
)
+
∞
∞
−
=
;yD
б) функция не является четной и
нечетной
в)
3ln
3
'
x
y =
г) 0х: у = 0 – пересечений нет, 0у: х = 0, у = 2
д)
0' ,0' ≠> yy , следовательно функция возрастает.
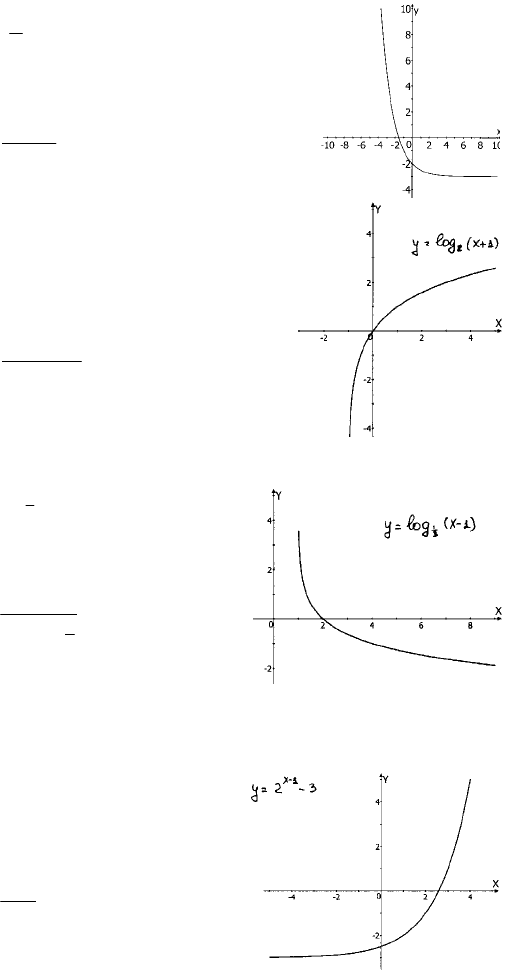
224
2)
3
2
1
−=
⎟
⎠
⎞
⎜
⎝
⎛
x
y
а)
() ( )
+∞∞−= ;yD
б) функция не является четной и нечетной
в)
()
()
5,0ln
5,0
'
x
y =
г) 0х: у = 0 – пересечений нет
0у: х = 0, у = -3
д)
0' ,0' ≠> yy
, следовательно функция
возрастает
3)
()
1log
2
+= xy
а) D(y): x + 1 > 0, т.е. х > - 1
б) функция не является четной и нечетной
в)
()
2ln1
1
'
+
=
x
y
г) 0х: у = 0, х = 0; 0у: х = 0, у = 0
д) y′ > 0 при x > -1 — функция возрас-
тает
y′ < 0 при х < -1, но на данном промежутке функция не существует.
4)
()
1log
3
1
−= xy
а) D(y): x – 1 > 0, x > 1
б) функция не является четной и не
является нечетной
в)
()
3
1
ln1
1
'
−
=
x
y
г) 0х: у = 0, х = 2
0у: х = 0 – пересечений нет
д) y’ > 0 при x > 1, функция возрастает
y’ < 0 при x < 1, но функция на данном промежутке не существует.
№ 1298
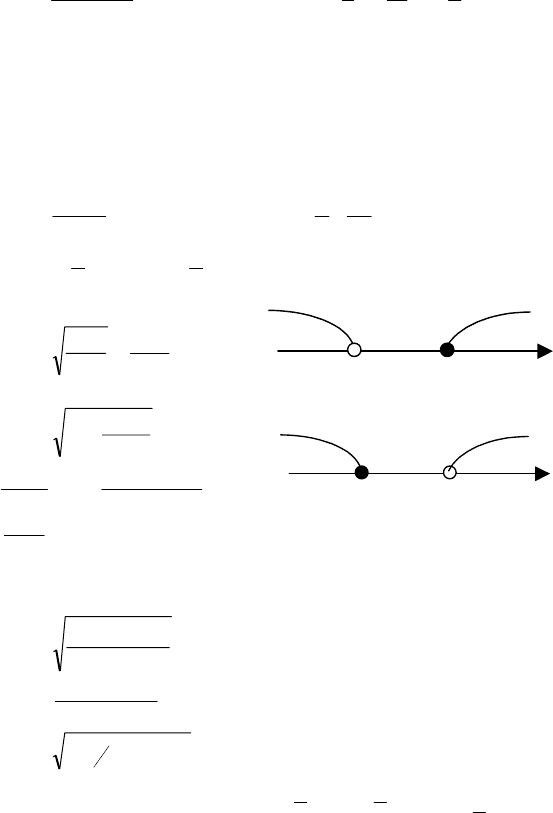
1) 32
1
−=
−x
y
а) D(y):
()
+∞−∞∈ ;x
б) функция не является четной и не
является нечетной
в)
2ln
2
'
1−
=
x
y
г) 0х: у = 0, х = log
2
3+1
0y: x = 0, y = -2,5
225
д) y’ > 0 при x > -2
y’ < 0 при x < -2, но на данном интервале функция не существует
2).
3)2(log
2
++= xy ; а) Д(у) : х+2>0; х>-2;
б) функция не обладает свойствами четности или нечетности;
в)
2ln)2(
1
'
+
=
x
y
; г) Ох : у=0 при
8
7
1
8
15
8
1
2 −=−=+−=x
;
Оу : х=0 при у=4;
д). у′>0 при х>-2; у'<0 при х<-2, но на этом интервале функция не суще-
ствует, следовательно, данная функция возрастает на области определения.
№ 1299
1)
()
xy
x
36lg2 −+= , D(y): 6 – 3x > 0, x < 2;
2)
()
42ln23 +−
−
x
x
, D(y): 2x + 4 > 0, x > -2;
3)
x
y
2cos
1
=
,
()
Zn
n
xxyD ∈
π
+
π
≠≠ ,
24
,02cos : ;
4)
4
x
tgy =
,
()
Znnx
x
yD ∈π+π≠≠ ,42 ,0
4
cos : .
№ 1300
1)
3
3
+
−
=
x
x
y
,
0
3
3
≥
+
−
x
x
D(y):
()
[
)
+
∞−−∞∈ ;33; Ux
2)
6
12
log
3
−
+
=
x
x
y
0
6
7
;0
6
612
;1
6
12
≥
−
+
≥
−
+−+
≥
−
+
x
x
x
xx
x
x
D(y):
(
]
(
)
+
∞−−∞∈ ;67; Ux .
№ 1301
1)
1112
166
2
2
+−
−−
=
xx
xx
y
,
()
()()
()()
(
]
(
]
()
+∞−∞−∈≥
−−
+−
;118;12; ;0
111
28
: UUx
xx
xx
yD ;
2)
()
13log
2
1
−−= xy ,
()
⎥
⎦
⎤
⎜
⎝
⎛
∈
⎪
⎩
⎪
⎨
⎧
>
≤
⎪
⎩
⎪
⎨
⎧
>−
≤−
⎩
⎨
⎧
>−
≥−−
2
1
3;3;
3
2
1
3
;
03
2
1
3
;
03
013log
:)(
2/1
x
x
x
x
x
x
x
yD .
+
–
3
+
–
3
+
–
6
+
–
7
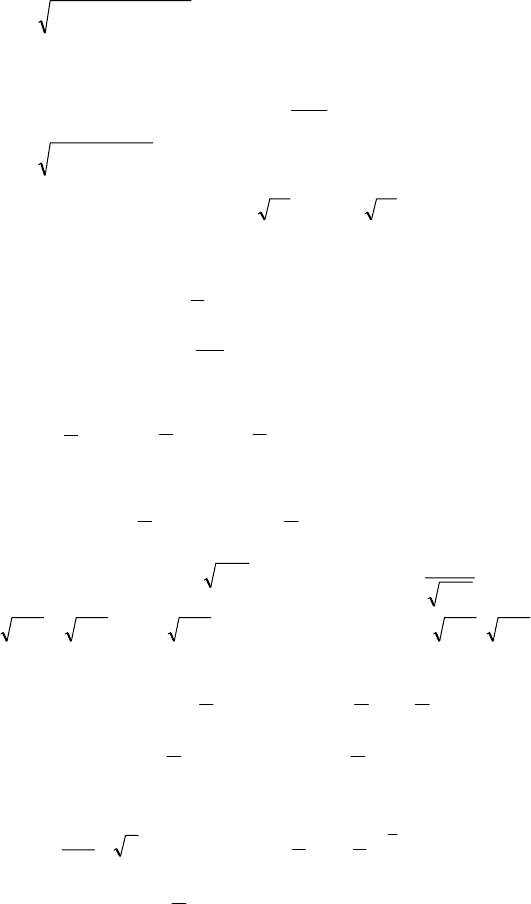
226
№ 1302
1)
()
75log
2
8,0
+−= xxy ,
()
()
;
075log
075
2
8,0
2
⎪
⎩
⎪
⎨
⎧
≥+−
>+−
xx
xx
yD
0750;075
22
>+−⇒<=+− xxDxx
;
2
15
;065;175
2,1
22
±
=≤+−≤+−
xxxxx ;
(
)
()
⎩
⎨
⎧
∈
+∞∞−∈
3;2
;
x
x
()
3;2∈x ;
2)
()
9log
2
5,0
−= xy ,
()
()
[
) (
]
10;33;10 ;
09log
09
:
2
5,0
2
∪−−∈
≥−
>−
⎪
⎩
⎪
⎨
⎧
x
x
x
yD .
№ 1303
1) 36
2
++= xxy , 6 след. ,6 ,3
2
6
00
−≥−=−=−= yyx ;
2)
182
2
−+−= xxy , 7 след. ,7 ,2
4
8
00
≤==
−
−
= yyx ;
3)
1+=
x
ey , e
x
> 0, след. y > 1;
4)
x
y
2
2 +=
, 2 0
2
,0 ;
2
2 ≠⇒≠≠=− y
x
x
x
y .
№ 1304
1)
⎟
⎠
⎞
⎜
⎝
⎛
π
−+=
4
sin5,0 xy
,
[]
5.1;5,0 след. ,1
4
sin1 −∈≤
π
−≤−
⎟
⎠
⎞
⎜
⎝
⎛
yx ;
2)
()
;
25,1
5,0
cos;cos25,1;sincos5,0 arxyxxy =α−α=+=
[
]
25,1;25,1 след. ,1sin1 ;25,1cos25,125,1 −∈≤≤−≤≤− yxx
№ 1305
1)
()
2
,cossin
0
π
=+=
xxxxf ,
()
1
2
sin
2
cos' −=
π
−
π
== xfk ;
2)
()
6
,3cos
0
π
== xxxf ,
()
3
2
sin3'
0
−=
π
−== xfk .
№ 1306
1)
()
1 ,
4
1
0
2
=−= xx
x
xf ,
()
2
1
3
2
1
2
1
'
−
−
−−= xxxf ,
()
4
,11'
π
−=αα=−= tgf ;

227
2)
()
3
1
,2
0
== xxxxf ,
()
2
1
2
3
3'2' xxxf ==
⎟
⎠
⎞
⎜
⎝
⎛
,
3
,3
3
1
'
π
=αα==
⎟
⎠
⎞
⎜
⎝
⎛
tgf .
№ 1307
1)
()
4
1
,
4
3
0
== x
xx
xf ,
(
)
(
)
(
)
000
' xxxfxfy
−
+
=
,
()
2
5
2
3
8
9
'
4
3
'
−
−
−==
⎟
⎠
⎞
⎜
⎝
⎛
xxxf , 36
4
1
' −=
⎟
⎠
⎞
⎜
⎝
⎛
f ,
xyxy 3615 ;
4
1
366 −=−−=
⎟
⎠
⎞
⎜
⎝
⎛
2)
()
1 ,42
0
24
−=+−= xxxxf
,
(
)
(
)
(
)
000
' xxxfxfy
−
+
=
,
(
)
xxxf 28'
3
−=
,
(
)
61'
−
=
−
f ,
(
)
xyxy 61 ;165
−
−
=
+
−
=
.
№ 1308
)(1
3
xfxxy =+−= . Точка пересечения (0,1), т.е. х
0
= 0,
() ( )( )
00
' xxxfxfg −+= ,
(
)
13'
2
−= xxf
,
(
)
,10' kf
=
−
=
следовательно к=–1.
№ 1309
2 ),(13
3
==−= yxfxy
, 1 ,132
3
=−= xx ,
()
91;9)(
2
=
′
=
′
fxxf
,
(
)
9191'
=
⋅
=
=
fk .
№ 1310
34 −= xy ,
2
26 xxy +−= .
Приравняем
2
26 и 34 ххх +−− ,
2
2634 xxx +−=− ,
096
2
=+− xx ,
()
03
2
=−x , 9 ,3
=
=
yx . Ответ: (3; 9).
№ 1311
1694
23
++−= xxxy , 61812'
2
+−= xxy .
По условию
()
0
0
=
= xyk , где х
0
– точка касания;
061812
2
=+− xx , 0132
2
=+− xx ,
25,2 ,2 ;5,0 ,1
2121
==== yyxx . Ответ: (1;2), (0,5;2,25).
№ 1312
,
4
,1x7
2
x3y
π
=α++=
тогда
(
)
,xy'1tg
0
=
=
α
где х
0
– точка каса-
ния;
3 ,1 ,176'
−
=
−
=
=+= yxxy . Ответ: (-1;-3).
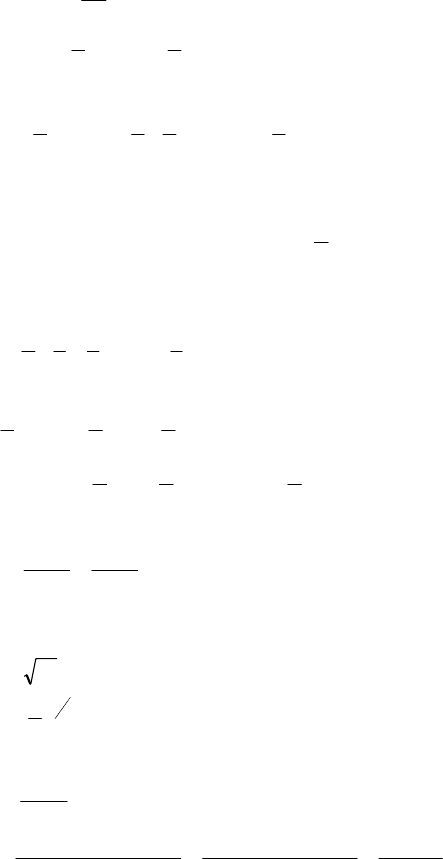
228
№ 1313
1)
()
5,0 ,2ln
0
=
= xxxxf ,
(
)
(
)
(
)
000
' xxxfxfy
−
+
=
,
()
1x2ln2
x2
x
x2lnx'f +=⋅+=
,
(
)
105,0'f
+
=
,
2
1
xy ;
2
1
x10y −=−+=
⎟
⎠
⎞
⎜
⎝
⎛
;
2)
()
1 ,2
0
==
−
xxf
x
,
(
)
(
)
(
)
000
' xxxfxfy
−
+
=
,
(
)
2ln2'
x
xf
−
−= ,
()
2ln
2
1
1'f −=
,
()
()
2lnx2ln1
2
1
1x2ln
2
1
2
1
y −+=−−=
.
№ 1314
(
)
4;2 ,67
23
−+−−= Mxxxy ,
723'
2
−−= xxy
,
()
174122' =−−=y ,
(
)
12'
=
=
α
ytg ,
4
π
=α
.
№ 1315
1 ,
2
=⋅=
−
xexy
x
,
(
)
1'ytg
=
α
,
xx
exexy
−−
−⋅=
2
2' ,
()
eee
y
112
1' =−=
,
e
tg
1
=α
.
№ 1316
3
,
6
3cos
3
2 π
=
π
−=
⎟
⎠
⎞
⎜
⎝
⎛
xxy ,
4
,1
3
' ;
6
3sin2'
π
−=α−=
ππ
−−=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
yxy
.
№ 1317
()
3
1
3
+
=
x
xf
,
() ()( )
11'1 ;1 ,0
3
1
3
+−+−=−==
+
xffyx
x
,
(
)()
11' ;'
2
=−= fxxf
,
1
+
=
xy
.
№ 1318
()
4 ,1
3
=+= xxxf
,
(
)
(
)
(
)
44'4
−
+
=
xffy ,
() ()
34' ;
2
3
'
2
1
== fxxf ,
(
)
33 ;439
−
=
−
+
=
xyxy .
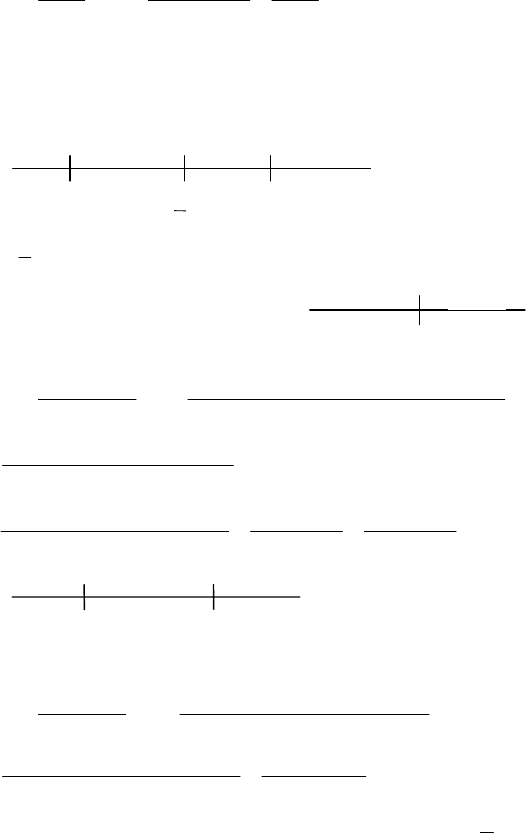
№ 1319
1) ;
1
1
2
2
−
+
=
x
x
y
(
)
(
)
() () ()
2
2
2
2
33
2
2
22
1
4
1
2222
1
1212
'
−
−
=
−
−−−
=
−
+−−
=
x
x
x
xxxx
x
xxxx
y
.
229
Функция возрастает при x < 0
2)
(
)
2
2
2
222
112
' ;
1
x
x
x
xx
y
x
x
y
+
=
−−
=
−
=
.
Функция возрастает при 0
≠
x
№ 1320
1)
()( )
23
21 −−= xxy ;
(
)
(
)
(
)
(
)
=−−+−−=
322
122213' xxxxy
()( )( )
(
)()
(
)
(
)
(
)
8521222321
22
−−−=−+−−−= xxxxxxx
+
+
–
+
1
5
8
2
5
8
x =
— точка максимума; 2x
=
— точка минимума;
2)
()
4
64 xy −+= ,
(
)
3
64' xy −−=
х = 6 — точка минимума.
№ 1321
1)
1
443
2
2
++
++
=
xx
xx
y
;
(
)
(
)
(
)
(
)
()
=
++
+++−+++
=
2
2
22
1
44312146
'
xx
xxxxxx
y
()
−
++
+++++
=
2
2
223
1
444666
xx
xxxxx
() ()
(
)
()
2
2
2
2
2
2
2
223
1
2
1
2
1
443886
++
+−
=
++
−−
=
++
+++++
−
xx
xx
xx
xx
xx
xxxxx
–
+
–
-2 0
х = -2 – точка минимума; х = 0 – точка максимума;
2)
43
36
2
+
++
=
x
xx
y
,
()()
()
=
+
++−++
=
⎟
⎠
⎞
⎜
⎝
⎛
2
43
36
2
34362
'
x
xxxx
y
() ()
,0
43
1583
43
918324266
2
2
2
22
>
+
++
=
+
−−−++
=
x
xx
x
xxxx
следовательно,
функция возрастает на всей числовой, за исключением точки
3
4
x −=
, в ко-
торой функция не определена.
Следовательно нет точек максимума и минимума.
–
+
6
