Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

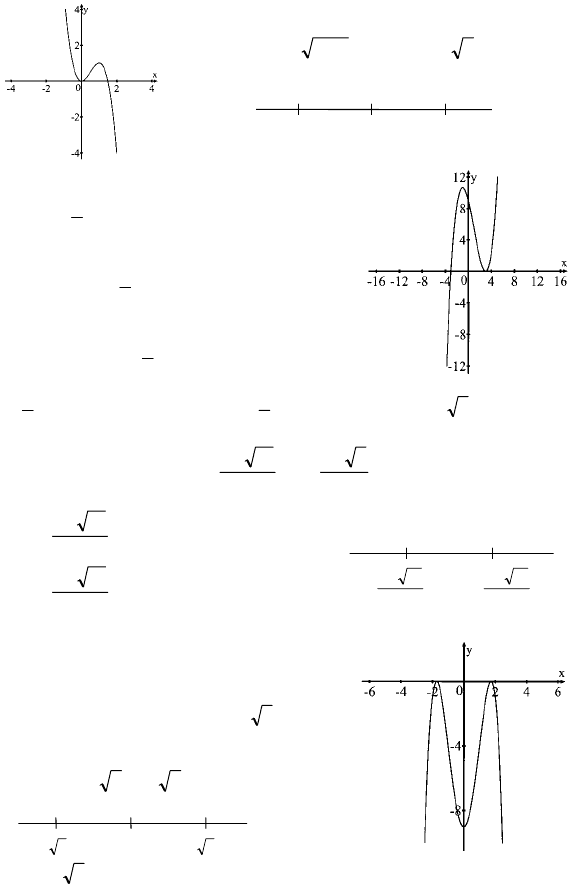
240
х = ± 1 – точка минимума
х = 0 – точка максимума
2) y = x
4
– 2x
2
–3
а) D(y) – R
б) f(-x) = x
4
– 2х
2
– 3 – функция четная
в)
(
)
,032 при 0
24
=−−= xxxf
21±±=x , след.
3±=x
г) f’(x) = 4x
3
– 4x = 4x(x-1)(x+1)
–
–
+
+
-1 0 1
№ 1352
1)
9x3xx
3
1
y
23
+−−=
а) D(y) = R
б)
()
9x3xx
3
1
xf
23
++−−=−
– функция
ни четная, ни нечетная
в)
()
,09x3xx
3
1
при 0xf
23
=+−−=
()()()
3 ,3 ,01
3
1
3,0333
3
1
22
±===
⎟
⎠
⎞
⎜
⎝
⎛
−−=−−− xxxxxxx
г)
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−=−−=
2
31
x
2
131
x3xxx'f
2
2
131
x
−
= – точка максимума
2
131
x
+
= – точка минимума
2) y = -
x
4
+ 6x
2
– 9
а) D(y) – R
б)
f(-x) = f(x) – функция четная
в)
f(x) = 0 при –x
4
+ 6x
2
– 9 = 0,
x
4
– 6x
2
+ 9 = 0, (x
2
– 3)
2
, 3x ±=
г)
()
(
)
=−−=+−= 34124'
23
xxxxxf
(
)
(
)
334 +−−= xxx
+
–
–
3−
0
3
+
3x ±= – точка максимума; х = 0 – точка минимума.
+
+
–
2
131 −
2
131 +
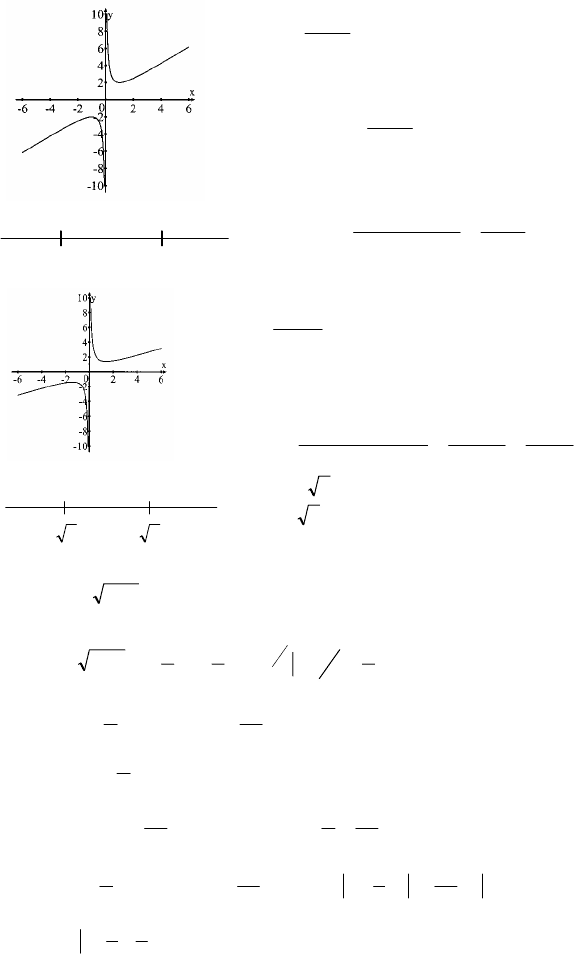
241
3)
x
1x
y
2
+
=
а) D(y):
x ≠ 0
б)
f(-x) = -f(x) – функция нечетная
в)
()
,0
x
1x
при 0xf
2
=
+
=
т.е. пересечений с
осью 0х нет.
г)
()
(
)
2
2
2
2
112
'
x
x
x
xxx
xf
−
=
+−⋅
=
х = -1 – точка максимума
х = 1 – точка минимума
4)
x2
2x
y
2
+
=
а) D(y):
x ≠ 0
б)
f(-x) = -f(x) – функция нечетная
в)
f(x) ≠ 0
г)
()
(
)
2
2
2
2
2
2
2
2
4
42
4
2222
'
x
x
x
x
x
xxx
xf
−
=
−
=
+−⋅
=
2x −= – точка максимума
2x = – точка минимума
№ 1353
1)
0y ,x3y ,1xy
321
=−=−=
, y
1
=y
2
, x–1 = 9–6x+x
2
, x
2
–7x+10=0, x=5,
x=2, но х – 1 ≥ 0 и 3 – х ≥ 0, след. х = 2 – точка пересечения y
1
и y
2
, тогда
()
6
7
2
1
1
3
2
1
2
1
1
2
1
2
3
2
1
=+−=⋅+−=
∫
xdxxS
2)
8
x
y ,xy ,
x
1
y
2
3
2
21
==−=
1x ;x
x
1
;yy
2
21
−==−=
- точка пересечения y
1
и у
2
0x ,
8
x
x ;yy
2
2
32
=== , ,2x ;
8
x
x
1
;yy
2
31
−==−= тогда
2ln
3
1
3
1
ln
24
1
3
1
ln
8
1
2
1
0
2
3
0
1
3
1
2
0
1
0
2
1
1
2
2
=−+=
=−+−=−+−=
−−
−
−−−
−
−
∫∫∫
x
xxxdx
x
dxxdx
x
S
+ +
–
-1 1
+
+
–
2− 2
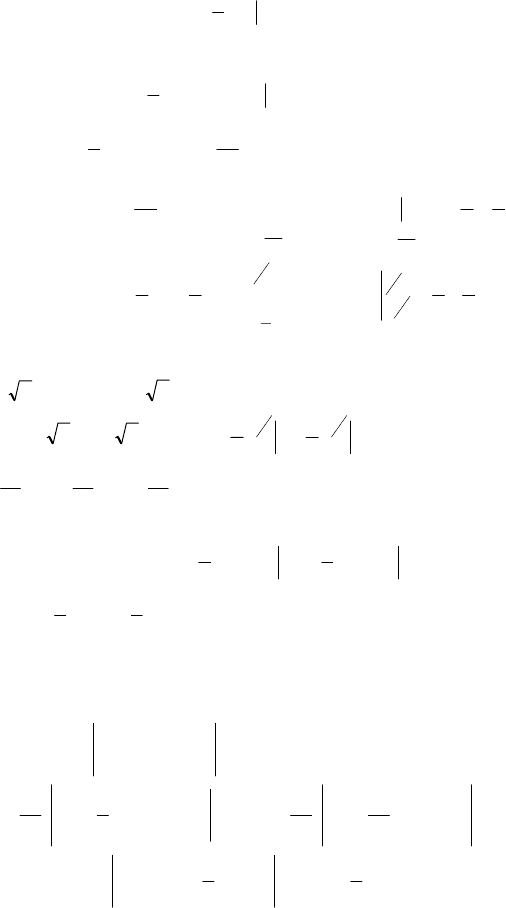
242
№ 1354
1) y
1
= 4x – x
2
, y
2
= 5, x = 0, x = 3
691815
3
1
215435
3
0
3
0
322
=+−=
⎟
⎠
⎞
⎜
⎝
⎛
−−=−−⋅=
∫
xxxxS ;
2) y =
x
2
– 2x + 8, y = 6, x = -1, x = 3,
()
3
28
2481
3
1
2499
248
3
1
2482
3
1
3
1
232
=−
⎟
⎠
⎞
⎜
⎝
⎛
−−−−+−=
=−
⎟
⎠
⎞
⎜
⎝
⎛
+−=−+−
∫
−
−
xxxdxxx
3)
π=
π
=== x ,
3
2
x ,0y ,xsiny
,
2
1
1cossin
3
2
3
2
−=−==
∫
π
π
π
π
xdxS =
2
1
4)
6
x ,
6
x ,0y ,xcosy
π
=
π
−===
,
1
2
1
2
1
xsinxdxcosS
6
6
6
6
=+===
∫
π
π
−
π
π
−
.
№ 1355
1) 9x,2y ,xy === , 4 ,2 == xx ,
3
16
10
3
16
18
3
16
8
10
3
2
3
2
82542
9
4
2
3
4
0
9
4
4
0
2
3
=−−+−=
=−+−=⋅−+−⋅=
∫∫
xxxdxxS
2) y =
x
2
+ 3, y = x + 5, x
2
+ 3 = x + 5, x
2
– x – 2 = 0, x
1
= -1, x
2
= 2,
()
()
5,4935,163
3
1
6
3
8
5,412
x3x
3
1
x5x
2
1
dx3xdx5xS
2
1
3
2
1
2
1
2
1
22
=−−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−−−+−+=
=
⎟
⎠
⎞
⎜
⎝
⎛
+−
⎟
⎠
⎞
⎜
⎝
⎛
+=+−+=
−
−−
−
∫∫
№ 1356
1) y = 9 – x
2
, y = (x – 1)
2
– 4, y
1
= 9 – x
2
, y
2
= x
2
– 2x – 3,
9 –
x
2
= x
2
– 2x – 3, 2x
2
– 2x – 12 = 0, x
2
– x – 6 = 0, x
1
= 3, x
2
= -2,
()
(
)
(
)
(
)
∫∫∫∫
−
−
−
−
−−
=−−−−−−−+−=
3
3
2
3
1
2
22
3
1
22
dx3x2xdxx9dx3x2xdxx9S
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
⎟
⎠
⎞
⎜
⎝
⎛
−−+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
−
−
−
−
−
−
1
1
2
3
2
2
3
1
3
23
3
3
3
3
33
93
3
1
3
9 xx
xx
xxxx
x
x
()
−
⎟
⎠
⎞
⎜
⎝
⎛
−++−−
⎟
⎠
⎞
⎜
⎝
⎛
−++−−+−+−= 927
3
8
1831
3
1
999927927
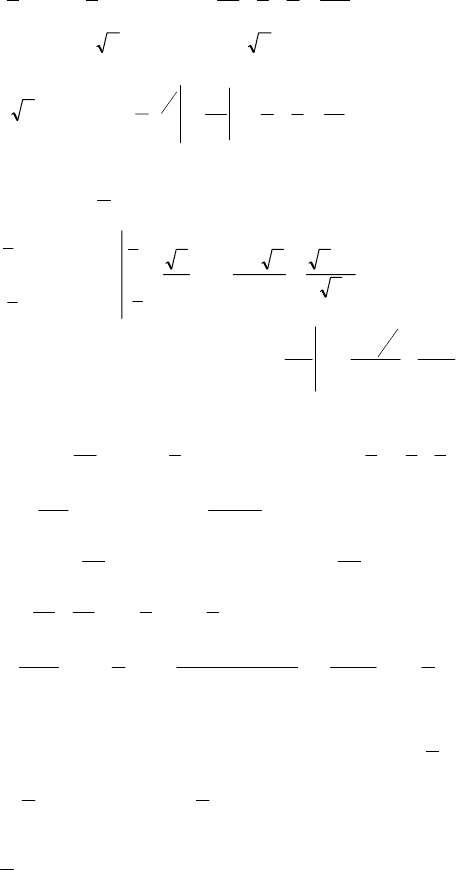
243
3
125
3
7
3
8
3
32
3664
3
8
31
3
1
=−−+=
⎟
⎠
⎞
⎜
⎝
⎛
−+++−−−
.
2)
3
2
2
1
xy ,xy == ,
(
)
01xx ,xx ,xx ,yy
56
3
2
21
=−=== ,
x = 0, x = 1 – точки пересечения
12
5
3
1
4
3
34
3
1
0
3
1
0
3
4
1
0
2
1
0
3
=−=−=−=
∫∫
x
xdxxdxxS
.
№ 1357
1)
0y ,
4
x ,xcosy =
π
==
,
2
12
2
22
1
2
2
xsinxdxcosS
4
2
4
2
+
=
+
=+===
π
π
−
π
π
−
∫
;
2) y = 3
x
, x = -1, x = 1, y = 0,
3ln3
8
3ln
3
1
3
3ln
3
dx3S
1
1
x
1
1
x
=
−
===
−
−
∫
.
№ 1358
1)
()
3
1
x,x
2
x
xxf
0
2
3
=+−= , f’(x) = 3x
2
– x + 1, 11
3
1
3
1
3
1
'f =+−=
⎟
⎠
⎞
⎜
⎝
⎛
;
2)
()
1x ,
x
xln
xf
0
==
,
() ()
11',
ln1
'
2
=
−
= f
x
x
xf
;
3)
()
3x ,x3
x
2
xxf
0
2
3
=+−=
−
,
()
3
x
x4
x3x'f
4
4
++−=
−
,
()
9
1
33
9
1
3
27
4
27
1
3'f =+=++−=
;
4)
4
x ,
xsin
xcos
y
0
π
==
,
xsin
1
xsin
xcosxsin
'y
22
22
−=
−−
= , 2
4
'y −=
⎟
⎠
⎞
⎜
⎝
⎛
π
.
№ 1359
1) f(x) = sin2x – x, f’(x) = 2cos2x – 1, 2cos2x – 1 = 0, cos2x =
2
1
;
Zn ,n2
3
x2 ∈π+
π
±=
,
Zn ,n
6
x ∈π+
π
±=
;
2)
f(x) = cos2x + 2x, f’(x) = -2sin2x + 2, 2 sin2x = 2, sin2x = 1,
Zn ,n
4
x ∈π+
π
=
;
3)
f(x) = (2x – 1)
3
, f’(x) = 3(2x – 1)
2
⋅ 2, 2x – 1 = 0, x = ½;
4)
f(x) = (1 – 3x)5, f’(x) = 5(1 – 3x)4 ⋅ (-3), 1 – 3x = 0, x = 1/3.
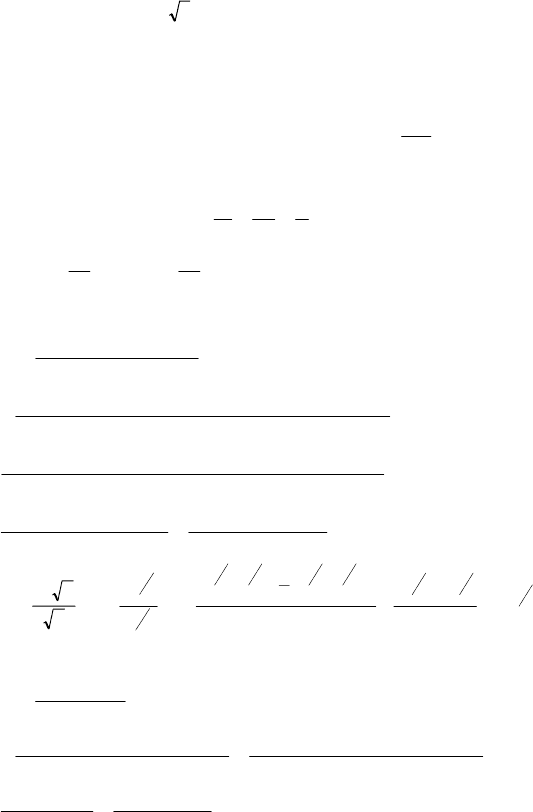
244
№ 1360
f(x) = (2x – 3)(3x
2
+ 1), f’(x) = 2(3x
2
+ 1) + 6x(2x – 3),
f’(1) = 8 – 6 = 2 ⇒ f’(1) = f’(0), f’(0) = 2.
№ 1361
()
3x18x5,1xxf
23
+−−= ,
(
)
18x3x3x'f
2
−−= , 018x3x3
2
<−− ,
06xx
2
<−− ,
()
(
)
02x3x
<
+
− ,
(
)
3;2x
−
∈
.
№ 1362
h = V
0
t – 4,9t
2
V
0
= 360м/с, V = h’ = V
0
– 9,8t,
V(10) = 360 – 98 = 262 м/с, h
max
при V
0
– 9,8t = 0 37
8,9
360
t ≈= сек.
№ 1363
48
2
t
kc2t 2 kt
3
3
π
=
π
=
ϕ
=⇒=π=ϕ=ϕ
,
22
t
4
3
kt3
π
==ω
,
()
π=⋅
π
=ω 1216
4
3
4
.
№ 1364
1)
3
235
x
3xx2x3x
y
+−+−
=
,
(
)
(
)
=
+−+−−−+−
=
3
2352324
x
3xx2x3xx3x1x4x9x5
'y
=
−+−+−−+−
=
3
34573457
x
x9x3x6x9x3xx4x9x5
x
9x2x2x2
x
x9x2x2x2
25
3
2347
−−−
=
−−−
=
;
2)
2
1
3
4
3
x
x6
y ;
x
xx6
y ==
,
6
1
6
5
6
5
3
4
2
1
2
1
3
1
x5
x
x3x8
x
6xx
2
1
xx8
'y
−
−
=
−
=
⋅⋅−⋅
= .
№ 1365
1)
1x
1x2x3
y
2
+
+−
= ,
()()
(
)
() ()
()
()
()
2
2
2
2
2
22
2
2
1x
1x2x3
1x
3x6x3
1x
1x2x32x2x6x6
1x
1x2x31x2x6
'y
+
−+
=
+
−+
=
=
+
−+−−−+
=
+
+−−+−
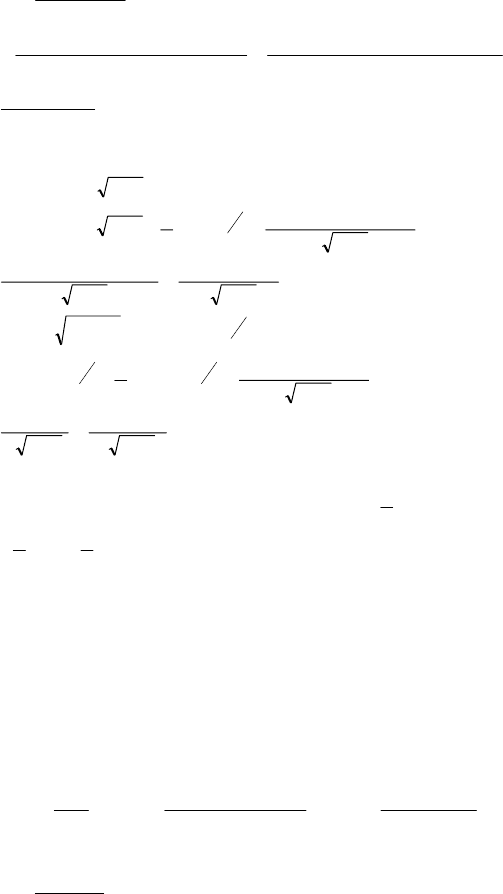
=
245
2)
1x2
1x3x2
y
2
+
+−
=
,
()()
(
)
() ()
()
2
2
2
22
2
2
1x2
5x4x4
1x2
2x6x43x6x4x8
1x2
1x3x221x23x4
'y
+
−+
=
=
+
−−−−−+
=
+
+−−+−
=
№ 1366
1)
()
1x1x2y
2
−+= ,
() ()
(
)
(
)
()
1x2
7x8x16
1x2
11xx2x28
1x2
11x1x242
1x
2
1
1x21x22'y
22
2
1
−
−−
=
−
+−+−
=
=
−
+−+⋅
=−+−⋅+=
−
2)
() ()
3
2
2
3
2
2
1xxy ;1xxy +=+= ,
() ()
(
)
()
33
2
3
2
3
2
2
3
2
1x3
3x4x2
1x3
x6x8
1x3
x21xx23
1xx
3
2
1xx2'y
+
+
=
+
+
=
=
+
++⋅
=+++=
−
3) y = sin2
xcos3x,
()
x5cos
2
5
xcos
2
1
x5cosxcos
2
3
x5cosxcosx3sinx2sin3x3cosx2cos2'y
−−=
=−−+=⋅−⋅=
4) y =
xcos2x, y’ = cos2x – 2xsin2x.
№ 1367
f(x) = (x - 1)(x – 2)(x – 3); f(x) = (x
2
– 3x + 2)(x – 3)
f’(x)=(2x–3)(x–3)+x
2
- 3x+2=2x
2
– 6x–3x + 9 + x
2
– 3x + 2 = 3x
2
– 12x + 11
3
x
2
– 12x + 11 = -1, 3x
2
– 12x + 12 = 0, 3(x
2
–4x+4)=0; 3(x – 2)
2
= 0, x = 2.
№ 1368
1)
()
2x23
xexf ⋅=
−
,
0e4e44e2)x('f
ex2xe2)x('f
111
x232x23
<−=⋅+⋅−=
⋅+⋅−=
−−−
−−
2)
()
x1
2
e
x
xf
−
= ,
()
()
x12
x12x1
e
exex2
x'f
−
−−
⋅+⋅
=
,
()
0
e
e4e4
2'f
2
11
>
+⋅
=
−
−−
.
№ 1369
()
x2sin1
x2sin1
xf
−
+
=
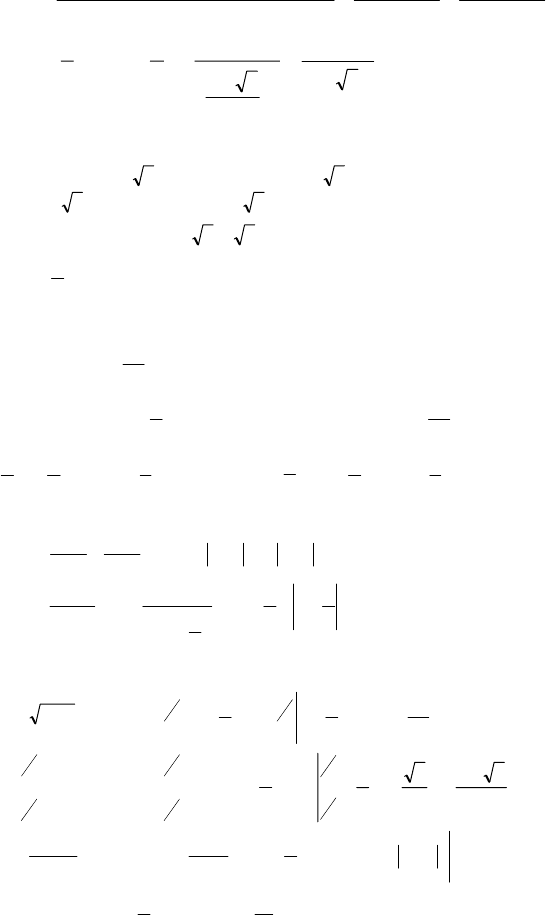
246
()
()
(
)
()
()()
222
2sin1
2cos4
2sin1
2cos22
2sin1
2sin12cos22sin12cos2
'
x
x
x
x
x
xxxx
xf
−
=
−
⋅
=
−
++−
=
()
()
22
32
8
2
32
2
6
' ;4
1
4
0'
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
⎟
⎠
⎞
⎜
⎝
⎛
π
== ff
№ 1370
()
()
13xxg
3xxxxf
23
+=
++=
;
(
)
()
3x'g
3x2x3x'f
2
=
++=
() ()
x'gx'f ≤ , 33x2x3
2
≤++ , 0x2x3
2
≤+ ,
(
)
02x3x
≤
+
,
⎥
⎦
⎤
⎢
⎣
⎡
−∈ 0;
3
2
x.
№ 1371
f(x) = cos3x, 1
24
F −=
⎟
⎠
⎞
⎜
⎝
⎛
π
.
Первообразная
,cx4sin
4
1
F +=
с найдем из условия
1
24
F −=
⎟
⎠
⎞
⎜
⎝
⎛
π
,
1c
8
1
;1c
6
sin
4
1
−=+−=+
π
⋅
,
,
8
1
1−=c
8
1
1x4sin
4
1
F −=
.
№ 1372
1)
1x
1
1x
1
y
−
−
+
=
,
c1xln1xlnF +−−+=
;
2)
⎟
⎠
⎞
⎜
⎝
⎛
−
=
−
=
4
1
x4
3
y ;
1x4
3
y,
c
4
1
xln
4
3
F +−= .
№ 1373
1)
() ()
(
)
4
45
12
4
3
1x
4
3
dx1xdx1x
4
9
2
3
4
9
2
3
1
9
2
3
=−=−=−=−
∫∫
;
2)
()
4
32
2
3
1
2
1
x2sin
2
1
xdx2cosdx1xcos2
4
6
4
6
4
6
2
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−===−
π
π
π
π
π
π
∫∫
;
3)
=
⎟
⎠
⎞
⎜
⎝
⎛
−++=
⎟
⎠
⎞
⎜
⎝
⎛
−
++=
−
+
∫∫
4
3
2
4
3
4
3
2
2xln7x2x
2
1
dx
2x
7
2xdx
2x
3x
()
2ln7
2
11
1ln76
2
9
2ln788 +=
⎟
⎠
⎞
⎜
⎝
⎛
++−++= .
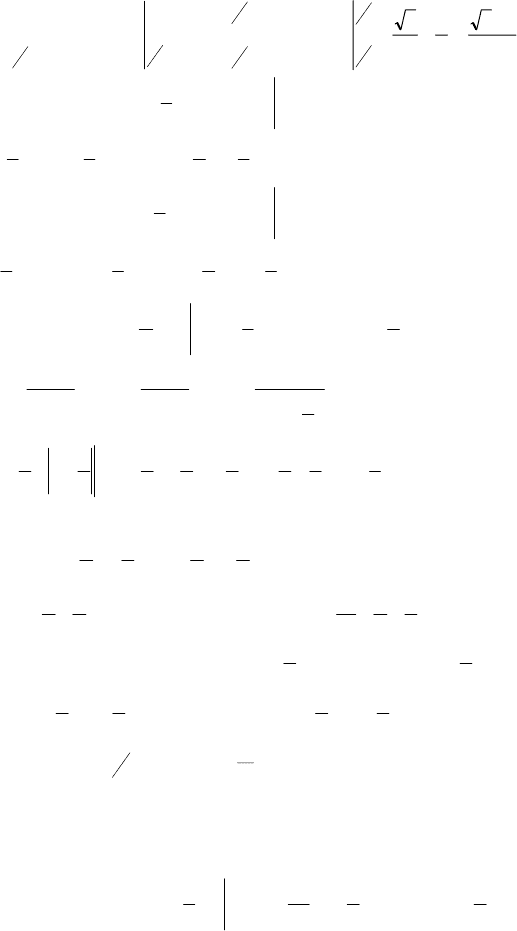
247
№ 1374
1) 1xcosxdxsin
2
2
=−=
π
π
π
π
∫
; 2)
2
13
2
1
2
3
xsinxdxcos
3
6
3
6
−
=−==
π
π
π
π
∫
;
3)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
++=++
−
−
∫
1
2
23
1
2
2
x3xx
3
1
dx3x2x
3
1
3
7
264
3
8
31
3
1
−=−=−+−++= ;
4)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
+−=+−
∫
2
1
23
2
1
2
x8x3x
3
1
dx8x6x
3
1
11
3
7
83
3
1
1612
3
8
=−=
⎟
⎠
⎞
⎜
⎝
⎛
+−−
⎟
⎠
⎞
⎜
⎝
⎛
+− ;
5)
()
()
3
2
2113
3
1
x
x
1
dx1x
3
1
3
1
2
=+−−
⎟
⎠
⎞
⎜
⎝
⎛
+−=
⎟
⎠
⎞
⎜
⎝
⎛
+−=+
∫
−
;
6)
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−=
−
−=
−
∫∫∫
−−−
1
1
1
1
1
1
dx
4
5
x4
2
dx
5x4
2
dx
x45
2
3ln
3
1
ln
9
1
ln
2
1
4
9
ln
4
1
ln
2
1
4
5
xln
2
1
1
1
=−=−=
⎟
⎠
⎞
⎜
⎝
⎛
−−=−−=
−
.
№ 1375
1)
2
1
4
x3cos =
⎟
⎠
⎞
⎜
⎝
⎛
π
− ,
Zn ,n2
34
x3 ∈π+
π
±=
π
−
,
Zn ,n2
43
x3 ∈π+
π
+
π
±=
. Ответ:
Zn ,n
3
2
912
x ∈π+
π
±
π
=
2) log
2
(3 – 2x) < -1,
()
2
3
x т т.,0x23 ,
2
1
logx23log
22
<>−<−
,
4
5
x ;
2
1
x23 ><−
. Ответ:
2
3
x
4
5
<<
3)
;22 ;25,024
2
a
2
2a3
2
a
a3
2
2
⋅−
+
==⋅
;02a3a ;a2a3 ;22
22a2a3
2
=++−=+=
−+
2a,1a
21
−
=
−
=
.
Ответ:
2a,1a
21
−=−=
4) y =
x(4 – x), x = 0, x = 4 – точки пересечения y = 4x – x
2
и y = 0, тогда
()
3
2
10
3
64
32x
3
1
x2dxxx4S
4
0
32
4
0
2
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−=−=
∫
. Ответ:
3
2
10

248
5)
3x
1
1x
9
4y
−
+
+
−=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≠
−≠
≥
−
+
+
−
3x
1x
0
3x
1
1x
9
4
()()()
(
)
()()
0
3x1x
1x3x93x1x4
≥
−+
++−−−+
,
(
)
()()
0
3x1x
1x27x93x2x4
2
≥
−+
+++−−−
,
()()
(
)
()()
0
3x1x
2x4
;0
3x1x
16x16x4
2
2
≥
−+
−
≥
−+
+−
,
(
)
(
)
⎪
⎩
⎪
⎨
⎧
−≠
−≠
+∞−∞−∈
3x
1x
;31;x U
Ответ:
()
(
)
+
∞−∞−∈ ;31;x U
.
6) y =
x
3
– 3x + a; [-2;0]; y
max
= 5,
y’ = 3
x
2
– 3, y’ = 0; 3(x - 1)(x + 1) = 0,
Максимальное значение на [-2;0] функ-
ция принимает в точке х = -1, у = 5 = -1 + 3 + a, откуда а = 3.
№ 1376
1) sin
2
x – 4sinx – 5 = 0, sinx = -1, sinx = 5, что невозможно, таким обра-
зом х
;Zn ,n2
2
∈π+
π
−=
Ответ:
0
2
3
x ;Zn ,n2
2
x >π=∈π+
π
−=
.
2)
f(x) = 3x
2
(1 – x) , [0;1]
f’(x) = 6x(1 – x) – 3x
2
= -9x
2
+ 6x =
= -3
x(3x – 2)
Точка максимума
3
2
x =
,
9
4
3
1
9
4
3
3
2
f =⋅⋅=
⎟
⎠
⎞
⎜
⎝
⎛
.
3) lg
x = lg3 – lg(3x – 8), x > 0,
,
3
8
x >
т.е.
3
2
2x >
,
8x3
3
x
−
=
; 3x
2
– 8x – 3 = 0,
3
54
3
9164
x
2
1
±
=
+±
= . Ответ: х = 3
4) y
1
= (x – 3)
2
, y
2
= 9, y
1
= y
2
; (x – 3)
2
= 9, x = 0, x = 6,
()
()
3627279254
x9x3x
3
1
254dx9x6x296S
3
0
23
3
0
2
=+−−=
=
⎟
⎠
⎞
⎜
⎝
⎛
+−−=+−−⋅=
∫
Ответ: 36.
+
+
–
-1 3
+ +
–
-1 1
+
– –
0
3
2
249
5)
()
0
2x
2,0
1x
1
25x
≤
+
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
Данное неравенство равносильно системе:
⎪
⎩
⎪
⎨
⎧
≠
≤
+
−
1x
0
2x
5x
(
]
⎩
⎨
⎧
≠
−∈
1x
5;2x
. Ответ:
(
)
(
]
.5;11;2x U
−
∈
6) y =
x
2
– 4x + 2, y = -2x + a, x
2
– 4x + 2 = -2x + a, x
2
– 2x + 2 – a =0,
D = 4 – 4(2 – a) = -4 + 4a = 4(a – 1), D ≥ 0 при a ≥ 1.
№ 1377
1)
()
42
x21log
7,0
>
+
, log
0,7
(1 + 2x) > 2, log
0,7
(1 + 2x) > log
0,7
0,7
2
,
100
49
x21 <+ ,
100
51
x2 −< ,
,021 но ,
200
51
>+−< xx т.е.
2
1
x −> .
Ответ:
200
51
2
1
−<<− x .
2)
f(x) = x
2
– x
3
, x
0
= -1, y = f(x
0
) + f’(x
0
)(x – x
0
), f’(x) = 2x – 3x
2
,
f’(x
0
) = -2 – 3 = -5, f(x
0
) = 2, y = 2 – 5(x + 1), т.е. у = -5х – 3.
3)
1x1x3x
24
−=−− ,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+−=−−
≥−
≥−−
1x2x1x3x
01x
01x3x
244
2
4
02x3x2
2
=−− ,
4
53
4
1693
2,1
±
=
+±
=x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥−
≥−−
−==
01x
01x3x
2
1
x,2x
2
4
21
Ответ: х = 2
4)
x
2
1
y,xy
21
== , y
1
= y
2
;
2
x
4
1
x ;x
2
1
x == ,
x
2
– 4x = 9; x(x – 4) = 0, x
1
= 0, x
2
= 4 – точки пересечения y
1
и у
2
, тогда
3
1
1
3
4
4
3
16
4x
3
2
24
2
1
dxxS
4
0
3
2
4
0
2
1
==−=−=⋅⋅−=
∫
.
5) y =
x
3
– 3ax2 + 27x – 5, y’ = 3x
2
– 6ax + 27 = 0, 3x
2
– 6ax + 27 = 0,
x
2
– 2ax + 9 = 0, при a = 3, x
2
- 2⋅ 3 ⋅ x + 9 = (x – 3)
2
, следовательно един-
ственная стационарная точка при а = 3.
6)
5x4xx
4
5
sin
2
+−=
π
,
1x
4
5
sin ≤
π
15x4x
2
≥+− , т.к. (х–2)
2
+1≥0, следовательно, равенство возможно только в
случае х=2, т.е. когда обе части уравнения принимают значение, равное 1.
