Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

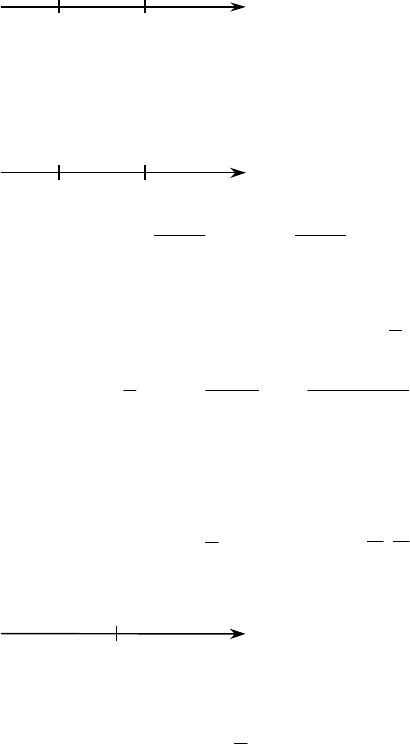
80
3)
21220)'265(')'22()(''
324235
−+=−+=+−+= xxxxxxxxxf ;
4)
xxxxxxxxf 1812)'594(')'653()(''
22334
−=+−=++−=
.
№ 954
1) f
′′
(x) = ((x + 1)
4
)′′ = (4(x + 1)
3
)′ = 12(x + 1)
2
,
f′′(x) > 0 при всех х ≠ -1, значит, функция при всех х ≠ -1 выпукла вниз
2) f
′′
(x) = (x
4
– 6x
2
+ 4)′′ = (4x
3
– 12x)′ = 12x
2
– 12,
f′′ > 0, 12(x
2
– 1) > 0, (х – 1)(х + 2) > 0,
-1
–
+
x
+
1
при x < -1 и x > 1, на этих промежутках функция выпукла вниз.
f
′′
(x) < 0 при –1 < x < 1, на этом промежутке выпукла вверх;
3) f′′(x) = ((x
2
– 3x + 2)e
x
)′′ = ((2x – 3)e
x
+ (x
2
– 3x + 2)e
x
)′ =
= (e
x
(x
2
– x – 1))′ = e
x
(x
2
– x – 1) + e
x
(2x – 1) = e
x
(x
2
+ x – 2)
f
′′
(x) > 0, x
2
+ x – 2 > 0,
-2
–
+
x
+
1
D = 1 + 8 = 9,
1
2
31
1
=
+
−
=x , 2
2
31
2
−=
−
−
=x ,
при x < -2 x > 1 – функция выпукла вниз,
f′′(x) < 0 при -2 < x < 1 – функция выпукла вверх;
4) f
′′
(x) = (x
3
– 6x ln x)′′ = (3x
2
– 6ln x – 6)′ =
⎟
⎠
⎞
⎜
⎝
⎛
−
x
x
6
6, x > 0,
f
′′
(x) > 0, 0
1
6 >
⎟
⎠
⎞
⎜
⎝
⎛
−
x
x ,
(
)
0
1
6
2
>
−
x
x
,
(
)
(
)
0
116
>
+−
x
xx
,
при x > 1 – функция выпукла вниз,
f
′′
(x) < 0 при 0 < x < 1 – функция выпукла вверх.
№ 955
1) f
′′
(x) = (cos x)′′ = (-sin x)′ = -cos x, f
′′
(x) = 0, -π < x < π,
-cos x = 0, cos x = 0,
Znnx ∈π+
π
= ,
2
,
2
;
2
π
π
−=x ;
2) f
′′
(x) = (x
5
– 80x
2
)′′ = (5x
4
– 160x)′ = 20x
3
– 160,
f
′′
(x) = 0, 20(x
3
– 8) = 0, x = 2.
2
–
+
x
При переходе через х = 2 f
′′
(x) меняет знак, значит, х = 2 – точка перегиба;
3) f
′′
(x) = (12x
3
– 24x
2
+ 12x)′′ = (36x
2
– 48x + 12)′ = 72x – 48
f
′′
(x) = 0, 24(3x – 2) = 0,
3
2
=x ,
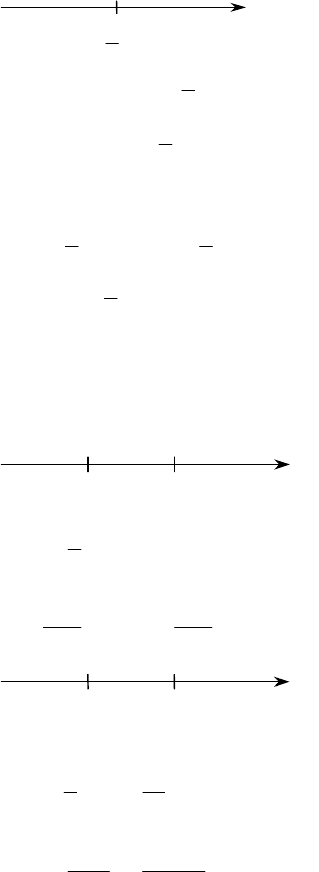
81
3
2
–
+
x
при переходе через
3
2
=x знак f′′(x) меняется, значит, это точка перегиба
4)
() ()
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−= '2coscos''2sin
2
1
sin'' xxxxxf
xxxx sin2sin22sin2sin
−
=
+−= , -π < x < π, f
′′
(x) = 0,
sin x(4cos x – 1) = 0, sin x = 0 x = πn, n ∈ Z, πn ∉ (-π; π),
4
1
cos =x
, nx
π
2
4
1
arccos +±=
,
4
1
arccos±=x
— являются точками перегиба.
Упражнения к главе IX.
№ 956
1) y′ = (2x
3
+ 3x
2
– 2)′ = 6x
2
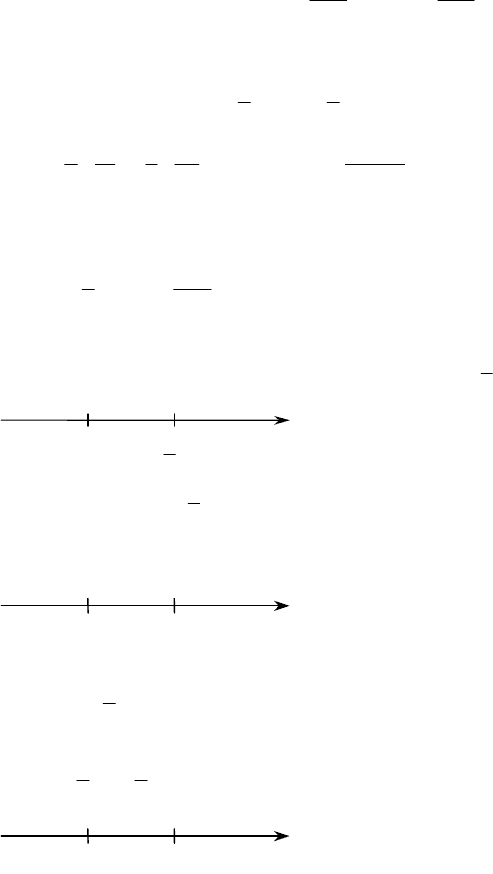
+ 6x, y′ > 0, 6x(x + 1) > 0,
+
+
–
-1 0
x
при x < -1, x > 0 – возрастает; y' < 0 при -1 < x < 0 – убывает;
2)
422'54
3
2
'
223
−−=
⎟
⎠
⎞
⎜
⎝
⎛
+−−= xxxxxy
,
y′ > 0, 2x
2
– 2x – 4 > 0, x
2
– x – 2 > 0, D = 1 + 8 = 9,
2
2
31
1
=
+
=x , 1
2
31
2
−=
−
=x ,
+
+
–
-1 2
x
при x < -1 x > 2 функция возрастает; y′ < 0 x
2
– x – 2 < 0,
при –1 < x < 2 – убывает;
3)
2
3
'1
3
'
x
x
y −=
⎟
⎠
⎞
⎜
⎝
⎛
−=
; х ≠ 0
y′ < 0 при всех х, но х ≠ 0 ⇒ значит, функция убывает при x < 0 и x > 0;
4)
()
2
3
2
'
3
2
'
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
x
x
y
; x ≠ 3,
y′ < 0 при x < 3 и x > 3 и убывает на этих промежутках.
82
№ 957
1) y′ = (x
4
– 4x
3
– 8x
2
+ 1)′ = 4x
3
– 12x
2
– 16x, y′ = 0, 4x(x
2
– 3x – 4) = 0;
⎢
⎣
⎡
=−−
=
043
0
2
xx
x
, D = 9 + 16 = 25,
4
2
53
1
=
+
=x
,
1
2
53
2
−=
−
=x
,
x
1
= 4, x
2
= -1, x
3
= 0;
2) y′(4x
4
– 2x
2
+ 3)′ = 16x
3
– 4x, y′ = 0, 4x(4x
2
– 1) = 0,
2
1
,
2
1
,0
014
0
321
2
−===⇒
⎢
⎣
⎡
=−
=
xxx
x
x
.
3)
2
12
3
1
'
12
3
'
x
x
x
y −=
⎟
⎠
⎞
⎜
⎝
⎛
+=
; x ≠ 0, y′ = 0, 0
3
36
2
2
=
−
x
x
,
x
2
– 36 = 0, x = ±6;
4) y′ = (cos2x + 2cos x)′ = -2sin2x – 2sin x, y′ = 0, -2sin x (2cos x + 1) = 0,
⎢
⎢
⎣
⎡
∈π+
π±
=
∈π=
⇒
⎢
⎢
⎣
⎡
−=
=
Znnx
Znnx
x
x
,2
3
2
,
2
1
cos
0sin
.
№ 958
1) y′ = (x
3
– 4x
2
)′ = 3x
2
– 8x, y′ = 0, x(3x – 8) = 0, x
1
= 0; x
2
=
3
8
,
+
+
–
0
3
8
x
x = 0 – точка max.,
3
8
=x
- точка min.;
2) y′ = (3x
4
– 4x
3
) = 12x
3
– 12x
2
, y′ = 0, 12x
2
(x – 1) = 0, x
1
= 0; x
2
= 1,
x = 0 – стационарная точка, х = 1 – точка min.
–
+
–
0 1
x
№ 959
1) xxxxy 55'3
2
5
'
425
−=
⎟
⎠
⎞
⎜
⎝
⎛
+−= , y′ = 0, 5x(x
3
– 1) = 0, x
1
= 0; x
2
= 1,
x = 0 – точка max., f(0) = 0 – 0 + 3 = 3, x = 1 – точка min.,
()
2
3
3
2
5
11 =+−=
f
;
+ +
–
0 1
x
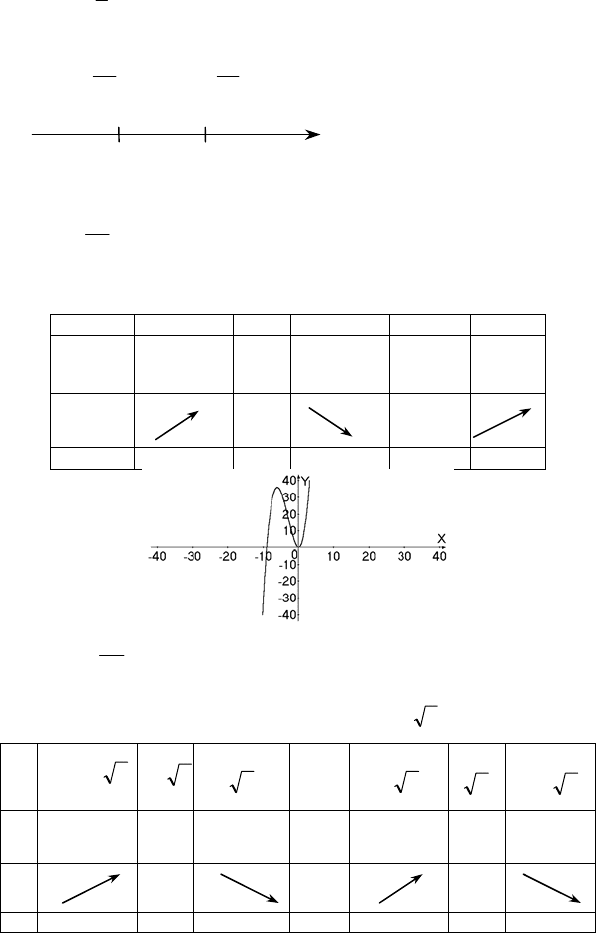
83
2)
xxxxy 8'34
5
1
'
425
−=
⎟
⎠
⎞
⎜
⎝
⎛
−−= , y′ = 0, x(x
3
– 8) = 0, x
1
= 0, x
2
= 2,
x = 0 – точка max., f(0) = 0 – 0 – 3 = -3, x = 2 – точка min.,
()
5
63
316
5
32
2
−=−−=f .
+
+
–
0 2
x
№ 960
1)
2
3
3
3
x
x
y +=
.
Область определения – R, y′ = x
2
+ 6x, y′ = 0, x(x + 6) = 0,
x
1
= 0; x
2
= -6 – стационарные точки
x x<-6 -6 -6<x<0 0 x>0
y′
+ 0 - 0 +
y 0
max min
2)
2
4
4
x
x
y +−=
.
Область определения – R,
y′ = -x
3
+ 2x, y′ = 0, x(2 – x
2
) = 0, x
1
= 0; x
2
= 2±
x
(
)
2;−∞−
2−
(
)
0;2−
0
(
)
2;0
2 2>x
y′
+ 0 - 0 + 0 -
y 1 0 1
max min max
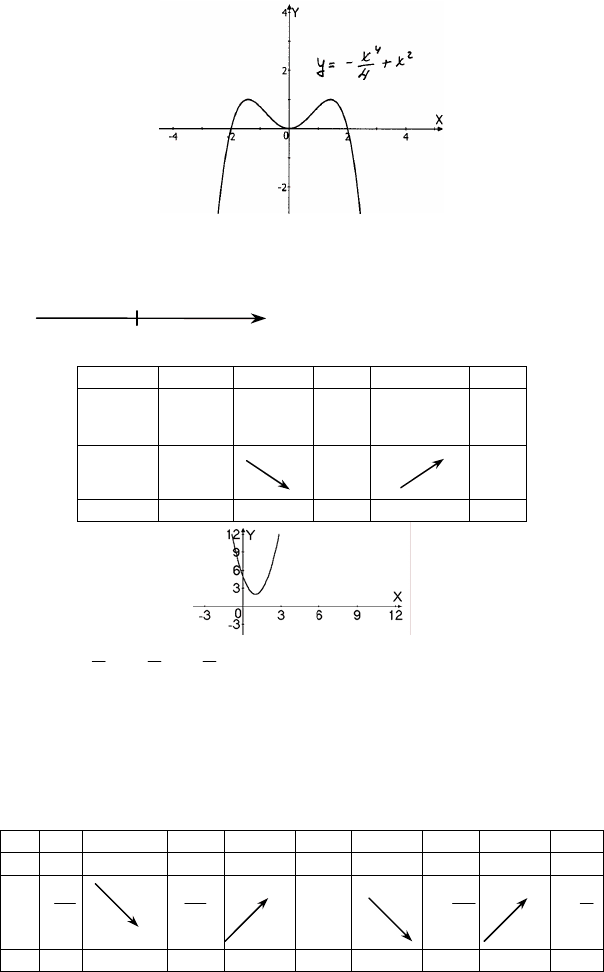
84
№ 961
1) у = 3х
2
– 6х + 5 на [0; 3]. Область определения [0; 3],
y′ = 6x – 6, y′ = 0, 6(x – 1) = 0, x = 1
1
–
+
x
x 0 (0; 1) 1 (1; 3) 3
y′
- 0 +
y 5 2 14
2)
2
2
3
3
2
4
1
234
+−−= xxxy на [-2; 4].
Область определния [-2; 4],
y′ = x
3
– 2x
2
– 3x, y′ = 0, x(x
2
– 2x – 3) = 0,
⎢
⎣
⎡
=−−
=
032
0
2
xx
x
,
D = 1 + 3 = 4,
x
1
= 3; x
2
= -1; x
3
= 0.
x -2 (-2;-1) -1 (-1;0) 0 (0;3) 3 (3;4) 4
y′
- 0 + 0 - 0 +
y
3
16
12
17
2
4
37
−
3
2
−
min max min

85
№ 962
1) f(x) = x
3
– 6x
2
+ 9 на [-2; 2], f(-2) = -8 – 6 ⋅ 4 + 9 = -23,
f(2) = 8 – 6 ⋅ 4 + 9 = -7, f′(x) = 3x
2
– 12x, f′(x) = 0, 3x(x – 4) = 0
x
1
= 0; x
2
= 4, 0 ∈ [-2; 2]; 4 ∉ [-2; 2], f(0) = 9,
[]
() ()
90max
2;2
==
−
fxf ,
[]
(
)
(
)
232min
2;2
−=−=
−
fxf ;
2) f(x) = x
3
+ 6x
2
+ 9x [-4; 0], f(-4) = -64 + 6 ⋅ 16 + 9 ⋅ (-4) = -4, f(0) = 0,
f′(x) = 3x
2
+ 12x + 9 f′(x) = 0, 3(x
2
+ 4x + 3) = 0, D/4 = 4 – 3 = 1,
x
1
= -3; x
2
= -1, -3 ∈ [-4; 0]; -1 ∈ [-4; 0], f(-1) = -1 + 6 – 9 = -4,
f(-3) = -27 + 6 ⋅ 9 – 9 ⋅ 3 = 0,
[]
() ( )
(
)
414min
0;4
−=−=−=
−
ffxf ,
[]
(
)
(
)
(
)
003max
0;4
==−=
−
ffxf ;
3) f(x) = x
4
– 2x
2
+ 3 [-4; 3], f(-4) = 256 – 2 ⋅ 16 + 3 = 227,
f(3) = 81 – 9 + 3 = 75, f′(x) = 4x
3
– 4x, f′(x) = 0, 4x(x
2
– 1) = 0,
x
1
= 0; x
2,3
= ±1, -1 ∈ [-4; 3]; 1 ∈ [-4; 3]; 0 ∈ [-4; 3],
f(-1) = f(1) = 1 – 2 + 3 = 2, f(0) = 0 + 0 + 3 = 3,
[]
() ( )
(
)
211min
3;4
==−=
−
ffxf ,
[]
(
)
(
)
2274max
3;4
=−=
−
fxf ;
4) f(x) = x
4
– 8x
2
+ 5 [-3; 2], f(-3) = 81 – 8 ⋅ 9 + 5 = 14,
f(2) = 16 – 8 ⋅ 4 + 5 = -11, f′(x) = 4x
3
– 16x, f′(x) = 0, 4x(x
2
– 4) = 0,
x
1
= 0; x
2,3
= ±2, 0 ∈ [-3; 2]; 2 ∈ [-3; 2]; -2 ∈ [-3; 2],
f(0) = 0 + 0 + 5 = 5, f(-2) = f(2) = -11,
[]
() ( )
(
)
1122min
2;3
−==−=
−
ffxf ,
[]
(
)
(
)
143max
2;3
=−=
−
fxf .
№ 963
Пусть сторона прямоугольника равна х, тогда другая сторона равна
⎟
⎠
⎞
⎜
⎝
⎛
− x
p
2
.
Тогда диагональ вычислим как:
()
2
2
2
⎟
⎠
⎞
⎜
⎝
⎛
−+== x
p
xxfl .
Исследуем эту функцию на min
=
′
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−+=
′
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
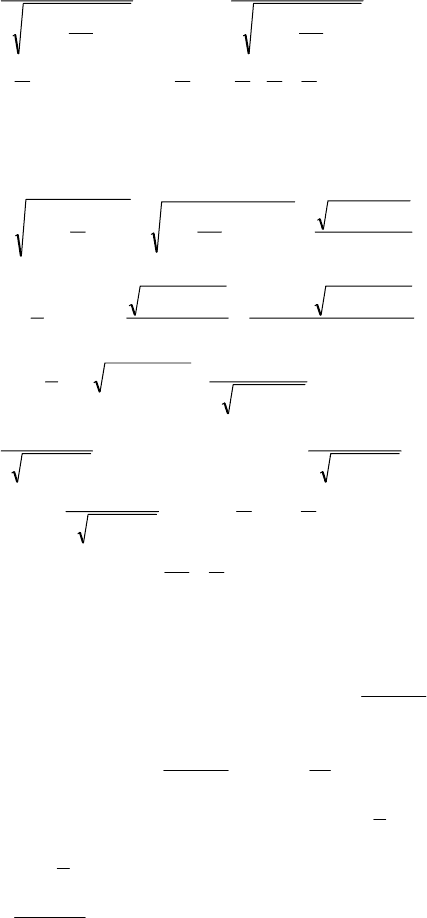
+−+=
′
px
p
xxpx
p
xxf
4
2
4
)(
2
22
2
2
86
px
p
x
px
−+
−⋅
=
4
22
)4(1
2
2
, f ′(х) = 0, 0
4
22
4
2
2
=
−+
−
px
p
x
px
, 4х – p = 0,
x =
4
p
, вторая сторона
4422
ppp
x
p
=−=−
– значит, это квадрат со сто-
роной р/4, ч.т.д.
№ 964
Пусть х – одна из равных сторон, значит другая тоже х и основание
(р–2х), тогда высота равна:
2
4
42
2
2
2
2
2
2
pxp
xpx
p
xx
p
xh
+−
=−+−=
⎟
⎠
⎞
⎜
⎝
⎛
−−=
,
тогда площадь вычислим как:
4
4)2(
2
4
)2(
2
1
)(
22
pxpxppxp
xpxS
+−−
=
+−
⋅−⋅⋅
,
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
⋅−
++−−=
′
2
2
42
4)2(
42
4
1
)(
ppx
pxp
pxpxS
()
2
2
22
2
44
124
84164
48
1
ppx
xpp
xpppxp
ppx −
−
=−+−+
−
= ,
S ′(х) = 0,
0
42
)3(4
2
=
−
−
ppx
xpp
, х =
3
p
, х =
3
p
– точка max.,
основание
33
2
2
pp
pxp =−=−
.
Это равносторонний треугольник.
№ 965
Пусть сторона квадрата равна х и высота h, тогда площадь поверхности
равна: р = 2 (х
2
+ хh + хh) = 600, х
2
+ 2хh = 300, h =
x
x
2
300
2
−
.
Найдем объем:
V = f (x) = x ⋅ x ⋅ h = x
2
⋅
x
x
2
300
2
−
= 150х –
2
3
x
.
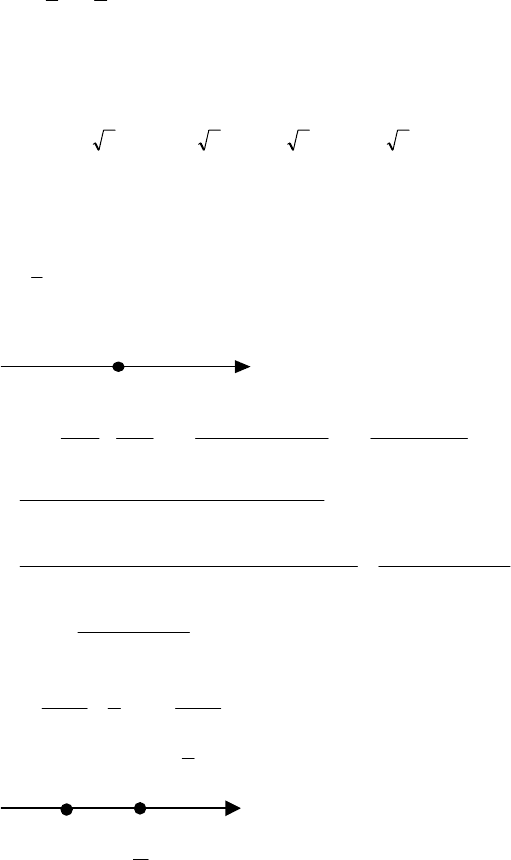
Найдем максимум функции V = f(x): f ′(х) = 150 –
2
2
3
x
,
f ′(х) = 0,
2
2
3
x
= 150, x
2
= 100, x = ±10, но x > 0 (по условию),
10
20
100300
=
−
=h , значит это куб.
87
№ 966
7795,127
3
7
5
9
2435
+−=
′
⎟
⎠
⎞
⎜
⎝
⎛
++−=
′
xxxxxy ,
у′ = 0, 9х
4
– 7х
2
+ 7 = 0; D = 49 – 252 < 0, значит 9х
4
– 7х
2
+ 7 > 0 и
у′ > 0 при всех х ∈ R, следовательно функция возрастает на всей области
определения, ч.т.д.
№ 967
у′ = (х + 2х x )′ = 1 + 3 x , 1 + 3 x > 0, т.к. x > 0, следовательно
у
′ > 0 при любых х ∈ R, и значит, функция возрастает на всей области
определения, ч.т.д.
№ 968
1) у′ = (х lnx) = lnx + 1, у′ = 0, lnx + 1 = 0, lnx = –1, lnx = lnе
–1
,
х =
e
1
– точка min;
2)
у′ = (хе
х
)′ = е
х
+ хе
х
= е
х
(1 + х), у′ = 0, е
х
(1 + х) = 0, х = –1,
х = –1 – точка min.
–
1
–
+
x
3)
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
−
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
+−−
=
′
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−
=
′
2110
1612
)3)(7(
9632575
3
9
7
25
2
xx
x
xx
xx
xx
y
()
=
+−
−−−+−−
=
2
2
2
2110
)102)(1612()2110(16
xx
xxxx
() ()
2
2
2
2
2
22
2110
2162416
2110
160321202433616016
+−
−−
=
+−
−++−−+
=
xx
xx
xx
xxxxx
,
у′ = 0, 0
2110
)2732(
2
2
=
+−
−−
xx
xx
; х
2
– 10х + 21 ≠ 0 ⇒ (х – 3) (х – 7) = 0
⇒ х ≠ 3, х ≠ 7, 2х
2
– 3х – 27 = 0, D = 9 + 216 = 225,
2
9
4
153
1
=
+
=x
,
3
4
153
2
−=
−
=x
,
3
−=x точка max.,
2
9
=x
точка min.
–
3
x
+
–
+
2
9
88
№ 969
рис 148 а)
1) возрастает
х ∈ (х
3
, х
5
) U (х
7
, х
8
); убывает х ∈ (х
1
, х
3
) U (х
5
, х
7
);
2)
х
max
= х
1
, х
5
; х
min
= х
3
, х
7
; 3) х
2
, х
4
, х
6
, х
8
;
рис 148 б)
1) возрастает
х ∈ (–10, –8) U (–4, –2) U (0, 4) U (6, 7);
убывает
х ∈ (–8, –4) U (–2, 0) U (4, 6);
2)
х
max
= –8; –2; 4; х
min
= –4; 0; 6; 3) –10; –6; –3; –1; 2; 5; 7.
№ 970
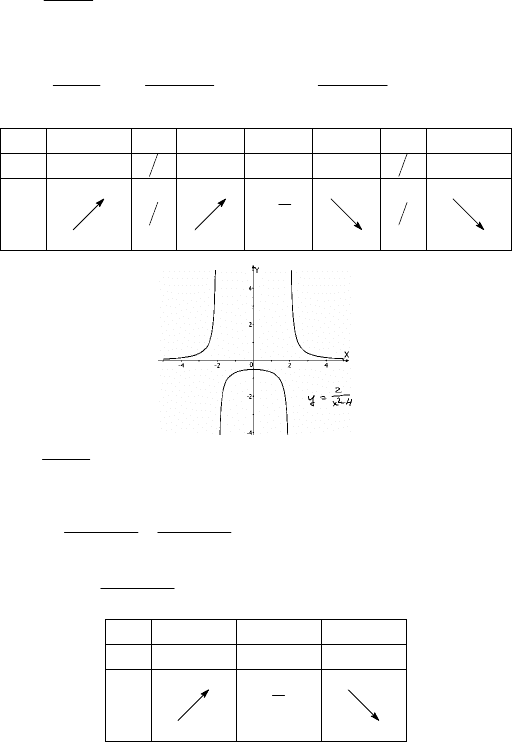
1)
4
2
2
−
=
x
y
а) Область определения
х ≠ ± 2
б)
у′ =
222
)4(
2
4
2
−
−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
− x
x
x
, у′ = 0,
22
)4(
2
−
−
x
x
= 0; x = 0;
x
(–∞; –2)
–2 (–2; 0) 0 (0; 2) 2
(2; +∞)
y′
+
∃
+ 0 –
∃
–
у
∃
2
1
−
max
∃
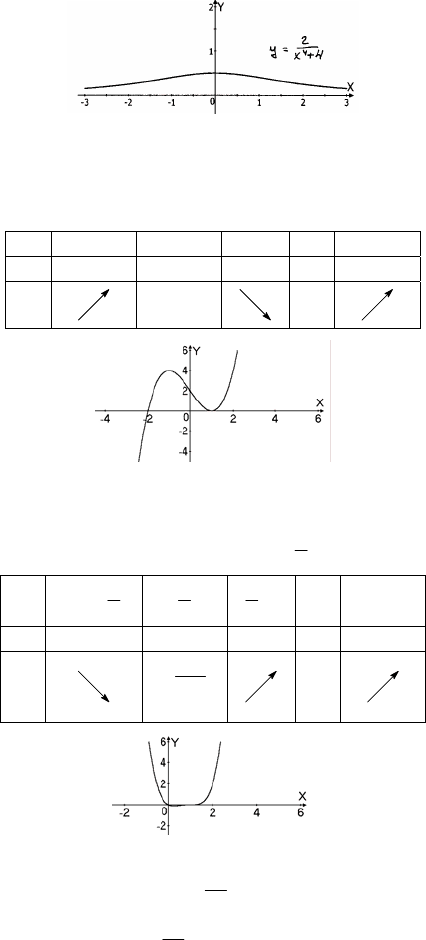
2)
4
2
2
+
=
x
y
а) Область определения R:
б)
2222
)4(
4
)4(
22
)(
+
−
=
+
⋅−
=
′
x
x
x
x
xy ;
в) у′(х) = 0,
0
)4(
4
22
=
+
−
x
x
, х = 0;
x
(–∞; –0)
0
(0; +∞)
y′
+ 0 –
у
2
1
max
89
3) у = (х – 1)
2
(х + 2)
а) Область определения R:
б) у′ = (х) = 2 (х – 1)(х + 2) + (х – 1)
2
= (х – 1)(2х + 4 + х – 1) =
= (х – 1)(3х + 3) = 3 (х – 1)(х + 1);
в) у′ = 0, 3 ⋅ (х – 1)(х + 1) = 0, х
1
= 1, х
2
= –1.
x
(–∞; –1)
–1 (–1; 1) 1
(1; +∞)
y′
+ 0 – 0 +
у
4
max
0
min
4) у = х(х – 1)
3
а) Область определения: R
б) у′ = (х – 1)
3
+ 3х (х – 1)
2
= (х – 1)
2
(х – 1 + 3х) = (х – 1)
2
(4х – 1)
в) у′ = 0, (х – 1)
2
⋅ (4х – 1) = 0, х
1
= 1 х
2
=
4
1
x
(–∞; –
4
1
)
4
1
(
4
1
; 1)
1
(1; +∞)
y′
– 0 + 0 +
у
256
27
−
min
0
№ 971
1) f(x) = 2sinx + sin2x; х∈[0;
2
3π
];
а) Область определения [0;
2
3π
]; б) f ′(х) = 2cosx + 2cos2x;
