Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

50
3) y
′=
2
x
5
5
1
−
, y′=0,
2
x
5
5
1
=
, x≠0, x
2
=25, x=±5.
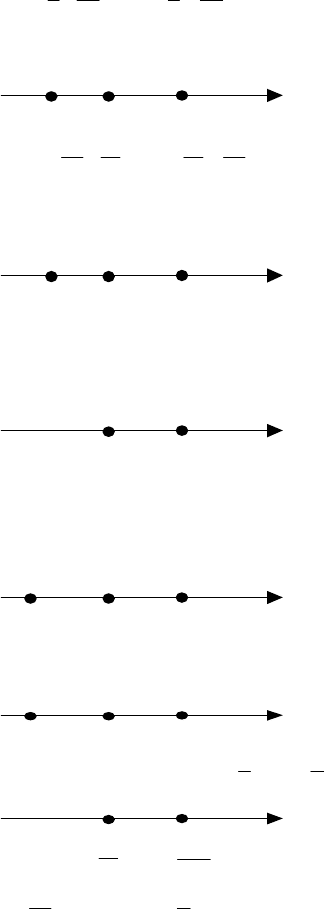
При переходе через точку х= –5 у
′ меняет знак с ‘+’ на’ ‘ , значит х= –5
– точка максимума, а через х=5 - с’–‘ на ‘+’, значит х=5 - точка минимума.
–
5
0
x
–
+
5
–
+
4) y
′=
16
14
2
+−
x
, y′=0,
2
4
16
1
x
= , x≠0, x
2
=64, x=±8.
При переходе через точку х= –8
у
′ меняет знак с ‘+’ на ’–‘ , значит х= –8 – точка максимума, а через х=8
с’–‘ на ‘+’, значит х=8 - точка минимума.
–
8
0
x
–
+
8
–
+
№ 915.
1) y′=3x
2
–6x, y′=0, 3x(x–2)=0 ⇒ x=0, x=2,
x=0 – точка максимума; x=2 – точка минимума;
у(0)=0
3
–3⋅0
2
, у(2)=2
3
–3⋅2
2
=8–12= –4;
0
x
+
–
2
–
2) y′=4x
3
–16x, y′=0, 4x(x
2
–2)=0 ⇒ x=0, x=2, х= –2,
x= –2 – точка минимума;
х=0 – точка максимума; x=2 – точка минимума;
f(–2)=(–2)
4
–8⋅(–2)
2
+3=16–32+3= –13,
f
′(0)=0
4
–8⋅0
2
+3=3 f ′(2)=2
4
–8⋅2
2
+3=16–32+3= –13;
–
–
2
0
x
+
–
2
+
3) y
′=1+cos x, y′=0, cos x = –1 ⇒ x=π+2πn, n∈Z.
При переходе через х=
π у′ не меняет знак, значит, х=π не является точ-
кой экстремума.
π−
π
–
x
+
–
+
π
3
4) y
′= –2sin x +1, y′=0, sin x =
2
1
⇒ x
1
=
6
π
+2πn, n∈Z;
6
π
x
+
–
+
6
5 π
x
2
=
6
5π
+2πn, n∈Z; x=
6
π
+2πn, n∈Z – точка максимума;
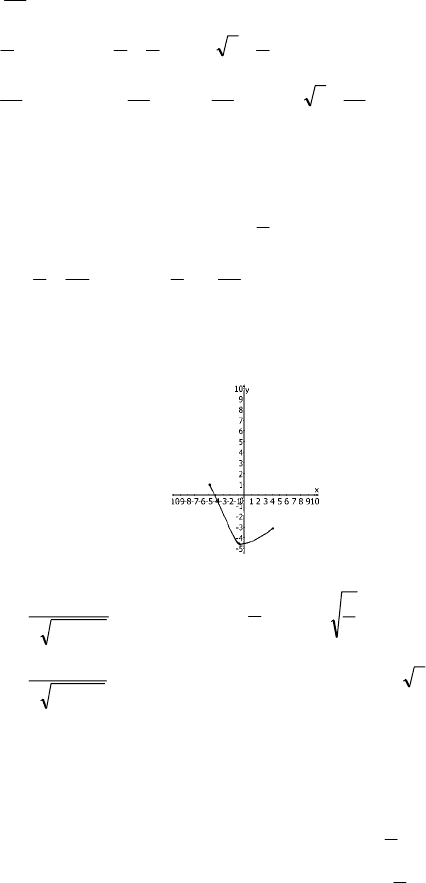
51
x=
6
5π
+2πn, n∈Z – точка минимума;
y(
6
π
+2πn)=2cos
6
π
+
6
π
+2πn= 3 +
6
π
+2πn,
y(
6
5π
+2πn)=2cos (
6
5π
+2πn)+
6
5π
+2πn= – 3 +
6
5π
+2πn, n∈Z.
№ 916.
1) y′=2, 2≠0 ⇒ нет точек экстремума;
2) y
′= –5, –5≠0 ⇒ нет точек экстремума;
3) y
′=3x
2
+2, y′=0 ⇒ 3x
2
+2=0 x
2
= −
2
3
– нет точек экстремума;
4) y
′=
1
2
1
х
2
+ , y′=0 ⇒
1
2
1
х
2
=− x
2
= –2 – не существует точек экстре-
мума. (Опечатка в ответе задачника).
№ 917.
1)
№ 918.
1) y′=
2
3x22
6x1
−
⋅
, 2–3x
2
=0 ⇒ x
2
=
2
3
⇒ x=±
3
2
, y′=0 ⇒ 6x=0 ⇒ x=0;
2) y
′=
(
)
xx
x
32
331
3
2
−
−
, x
3
–3x=0 ⇒ х(х
2
-3)=0 ⇒ х=0, x=± 3 ,
y
′=0 ⇒ 3x
3
–3x=0 ⇒ 3(x
2
–1)=0 ⇒ x=±1;
3) y
′=
1
1
1
1
<
>
⎩
⎨
⎧
− x
x
, x=1 – точка минимума;
4) y
′=0,
y
′=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−
⎩
⎨
⎧
−
⇒=
′
+
−
2
1
2
1
12
12
0
0
0
12
12
2
1
=x
=x
x=
x=
y
x<
x>
x
x
,
x=0 –также является критической точкой.
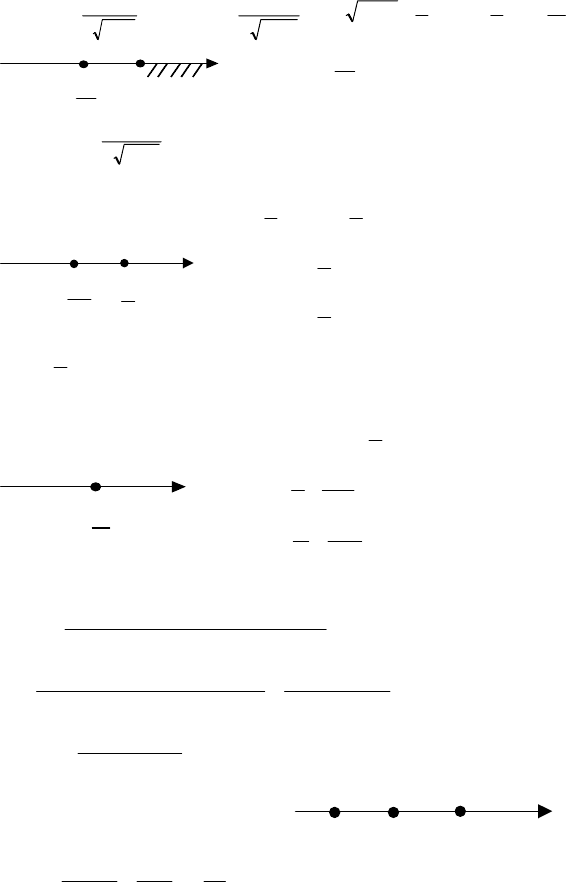
52
№ 919.
1) y′=1–
x32
1
−
, y′=0, x<3,
x32
1
−
=1⇒ 3x− =
2
1
⇒3–x=
4
1
⇒x=
4
11
,
4
11
x
+
–
+
3
x=
11
4
– точка максимума;
2) y
′=
1x7
16
−
⋅
, x>1
y
′=0 – нет решений
3) y
′=1–2cos 2x, y′=0, cos 2x=
2
1
⇒ 2x=±
3
π
+2πn, n∈Z;
6
π−
x
+
–
+
6
π
x=
6
π
+πn, n∈Z;
x=
6
π
+πn – точки максимума;
x= –
6
π
+πn – точки минимума;
4) y
′= –3sin 3x–3,
y
′=0 ⇒ –3(sin 3x+1)=0 ⇒ sin 3x= –1 ⇒ 3x=
2
π
−
+2πn, n∈Z
x
++
6
π
x=
3
n2
6
π
+
π
−
, n∈Z;
x=
−+
π
π
6
2n
3
– стационарная точка.
№ 920.
1) y′=
()()
()
3
)2)(3(2323
4
3
22
=
−
−−+−−−
x
xxxx
()()
()
(
)
()
3
2
4
2
3
)5(2
3
)2439(32
=
x
xx
x
xxxx
−
−−
=
−
−++−−−
y
′=0,
()
()
3
2
3
)5(2
x
xx
−
−−
=0 ⇒ x=2, x=5
x=2 – стационарная точка;
х=5 – точка максимума;
2
x
–
+
–
3
5
–
y(5)=
()
()
4
27
4
27
53
52
3
−=
−
=
−
−
;
53
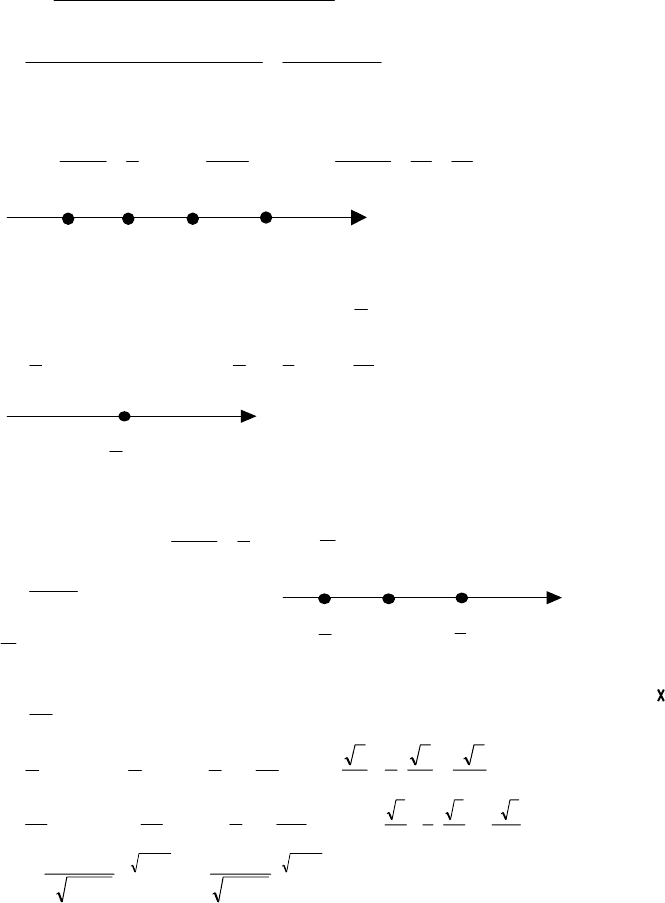
2) y′=
(
)
(
)
(
)
()
1 x
1
122)1(43
4
2322
≠=
−
−⋅+−−+
x
xxxxxx
()
()
()
3
23
4
2323
1
43
1
)4243(1-x
=
−
−−
=
−
−−−+
x
xxx
x
xxxxx
,
y′=0 x(x
2
–3x–4)=0, x= –1 – точка минимума; х=0 – точка максимума;
х=4 – точка минимума;
y(–1)=
4
1
)2(
21
2
=
−
+−
, y(0)= =
−
+
2
)1(
00
0, y(4)=
3
32
9
96
3
3264
2
==
+
;
–
1
0
x
+
–
+
1
4
–
+
3) y′=e
3 x
+3(x–1)e
3 x
=e
3 x
(1+3x–3)=e
3 x
(3x–2),
y′=0, e
3 x
(3x–2)=0 ⇒ e
3 x
>0 и 3х – 2 = 0 ⇒ x=
2
3
,
x=
3
2
– точка минимума, y(
3
2
)=
3
e
3
1
2
2
−=⋅− e ;
–
3
2
+
x
4) y′=cos x +cos 2x, y′=0, cos x +cos 2x=0,
cos x +cos
2
x–sin
2
x=0, 2cos
2
x+cos x–1=0,
D=1+8=9, cos x=
2
1
4
31
=
+−
⇒ x= ±
π
3
+2πn, n∈Z,
cos x=
−−13
4
= –1 ⇒ x=π+2πn, n∈Z,
x=
π
3
+2πn, n∈Z – точка максиму-
ма,
x=
5
3
π
+2πn, n∈Z – точка минимума,
y(
3
π
+2πn)=sin(
3
π
+2πn)+
2
1
sin(
3
2
π
+4πn)=
4
33
2
3
2
1
2
3
=⋅+ ,
y(
3
5
π
+2πn)=sin (
3
5
π
+2πn)+
2
1
sin(
3
10
π
+4πn)=
4
33
2
3
2
1
2
3
−=⋅−−
2
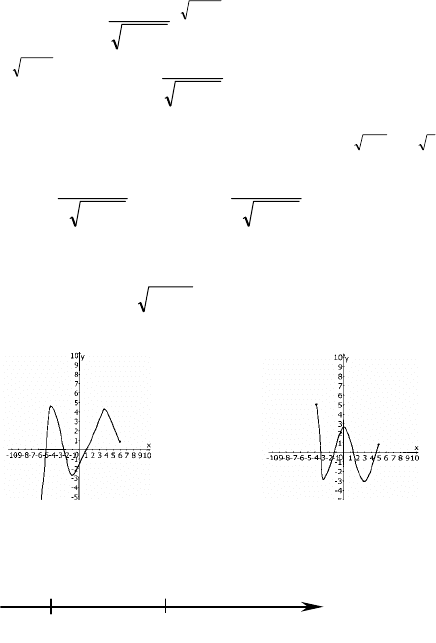
'
32
2
x
x
y
−
−
=
−=
−
2
3 x
e
2
3
2
3
x
e
x
x
−
−
;
π
x
–
–
+
π
3
5
3
π
54
0
'
=y
при
0
3
2
3
2
=
−
−
−x
e
x
x
, поскольку
0
2
3
>
−x
e , ищем
0
3
2
=
−
−
x
x
, откуда х=0;
При переходе через точку 0 производная у
’
меняет свой знак на отрица-
тельный, значит,
х=0 – точка минимума,
303
)0( eey ==
−
;
6).
xe
e
y
x
x
−
−
=
2
1
'
; 0'
=
y при 0
2
1
=
−
−
xe
e
x
x
;
0;;1;01
0
====− xeeee
xxx
при переходе через точку 0 производная
у’ меняет свой знак с отрицательного на положительный, значит, х=0 – точ-
ка минимума,
10)0(
0
=−= ey .
№ 921
№ 922
y′ = n(x + 1)
n-1
⋅ e
-x
– (x + 1)
n
⋅ e
-x
= (x + 1)
n-1
⋅ e
-x
(n – x – 1),
y
′ = 0, (x + 1)
n-1
⋅ e
-x
(n – x – 1) = 0,
–
–
+
–1
n - 1
х
n = 2k,
x = -1 – точка минимума, х = n – 1 – точка максимума
n = 2k + 1, (x + 1)n-1 = (x + 1)2k+1-1 = (x + 1)2k
≥ 0,
x = n – 1 – точка максимума.
§ 51 Применение производной
к построению графиков функции
№ 923
1) область определения: -7 ≤ х ≤ 7,
множество значений: -2
≤ f(x) ≤ 2;
2) y(x) = 0 при х
1
= -6, х
2
= -4, х
3
= 0, х
4
= 4, х
5
= 6;
3) функция возрастает при -5 < x < -2, 2 < x < 5,
функция убывает при -7 < x < -5, -2 < x < 2, 5 < x < 7;
55
4)
f(x) > 0 при –7 < x < -6, -4 < x < 0, 4 < x < 6,
f(x) < 0 при –6 < x < -4, 0 < x < 4, 6 < x < 7;
5) x
max
= -7, x
max
= -2, x
max
= 5, x
min
= -5, x
min
= 2.
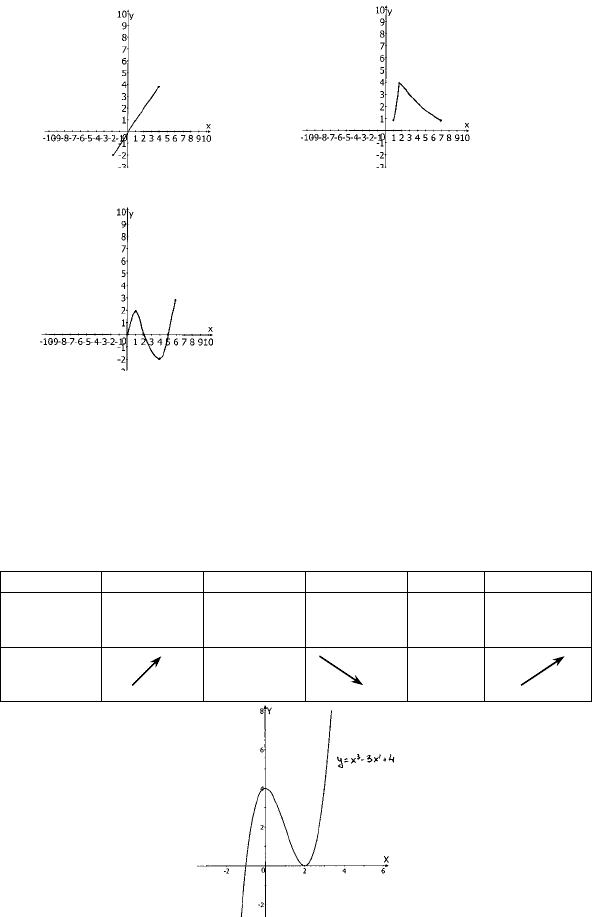
56
№ 924
1) 2)
№ 925
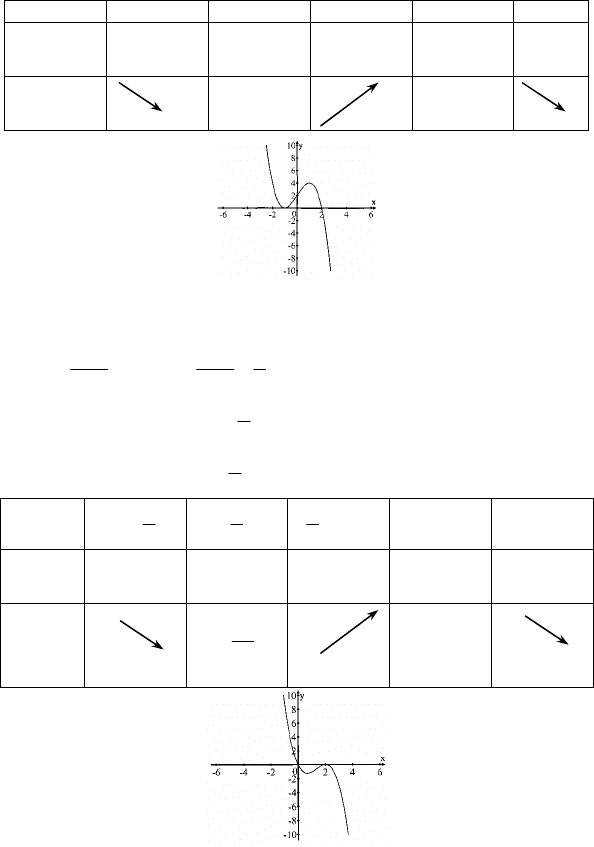
№ 926
1) у = х
3
– 3х
2
+ 4;
1.область определения – множество R; 2. y′ = 3x
2
– 6x;
3. y′ = 0, 3x(x – 2) = 0, x = 0, x = 2;
4. y′ > 0, x < 0, x > 2 – возрастает; у′ < 0, 0 < x < 2 – убывает;
5. х = 0 – точка max, т.к. при переходе через нее меняется знак y’ с «+» на «-».
у(0) = 4, х = 2 – точка min, т.к. при переходе через нее меняется знак y’
с «-» на «+».
у(2) = 8 – 12 + 4 = 0.
x x < 0 0 0 < x < 2 2 x < 2
F’(x) + 0 – 0 +
f(x) 4 0
57
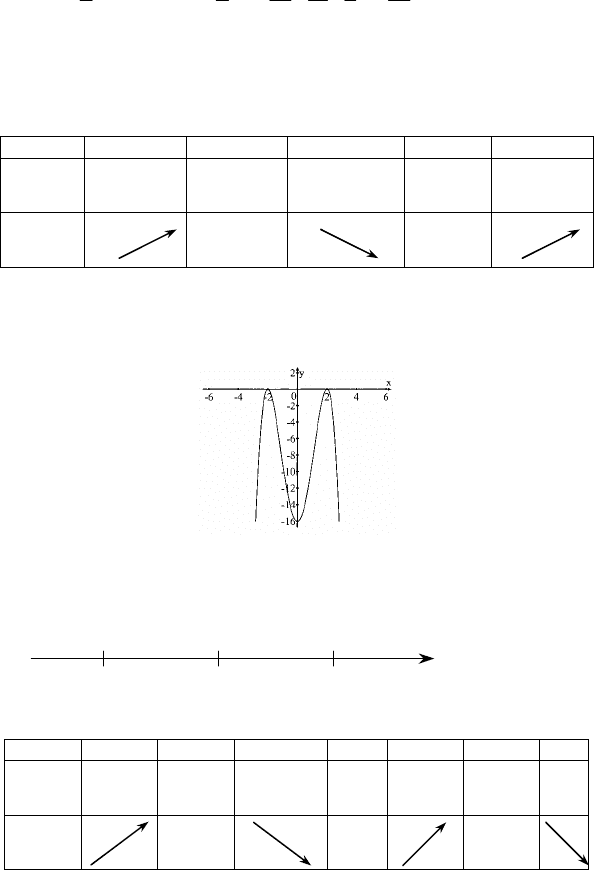
2) у = 2 + 3х – х
3
1. область определения – множество R; 2. y′ = 3 – 3x
2
3. y′ = 0 3(1 – x
2
)=0; x
2
– 1=0; x = 1, x = -1
4. y′ > 0; x
2
< 1; -1 < x < 1, y′ > 0; x
2
> 1; x < -1; x > 1;
5. x = -1 – точка минимума f(-1) = 2 – 3 + 1 = 0,
x = 1 – точка максимума f(1) = 2 + 3 – 1 = 4;
x x < -1 x = -1 -1 < x < 1 1 x > 1
F’(x) - 0 + 0 -
f(x) 4 0
3) у = -х
3
+ 4х
2
– 4х;
1. область определения – R; 2. y′ = -3x
2
+ 8x – 4;
3. y′ = 0; 3x
2
– 8x + 4 = 0 D = 16 – 12 = 4;
2
3
24
1
=
+
=x ,
3
2
3
24
2
=
−
=x ;
4. y′ > 0; 3x
2
– 8x + 4 < 0,
2x
3
2
<<
,
y′ < 0; 3x
2
– 8x + 4 > 0, 2x
3
2
<< x > 2.
x
x <
3
2
3
2
3
2
< x < 2
2 x > 2
F’(x) – 0 + 0 -
f(x)
27
32
−
0
58
5.
3
2
=x
- точка min
27
32
3
8
9
16
27
8
3
2
−=−+−=
⎟
⎠
⎞
⎜
⎝
⎛
f ,
x = 2 – точка max f(2) = -8 + 16 – 8 = 0;
4) y = x
3
+ 6x
2
+ 9x;
1. область определения – R; 2. y′ = 3x
2
+ 12x + 9;
3. y′=0; x
2
+4x+3=0, D=4–3=1, x
1
= -2 – 1 = -3, x
2
= -2 + 1 = -1;
4. y′>0; x
2
+4x+3>0, x>-3, x>-1, y′ < 0; x
2
+ 4x + 3 < 0, -3 < x < -1;
x x < -3 -3 -3 < x < -1 -1 x > -1
F’(x) + 0 – 0 +
f(x) 0 -4
5. x = -3 – точка max; f(-3) = -27 + 54 – 27 = 0,
x = -1 – точка min; f(-1) = -1 + 6 – 9 = -4.
№ 927
1) у = х
4
+ 8х
2
– 16
1. область определения – R;
2. y′ = -4x
3
+ 16x;
3. y′ = 0; -4x(x
2
– 4) = 0, x = 0, x = 2, x = -2;
4. y′ > 0; x(x – 2)(x + 2) < 0,
–
+
+
-2 0 2
–
x < -2, 0 < x < 2, y’ < 0 x(x – 2)(x + 2) > 0 -2 < x < 0 и x > 2.
X x < -2 -2 -2<x<0 0 0<x<2 2 x>2
f’(x) + 0 - 0 + 0 -
f(x) 0 -16 0
5. x = -2 – точка max; f(-2) = -16 + 32 – 16 = 0,
x = 0 – точка min, f(0) = -16; x = 2 – точка max, f(2) = -16 + 32 – 16 = 0;
2) y = x
4
– 2x
2
+ 2
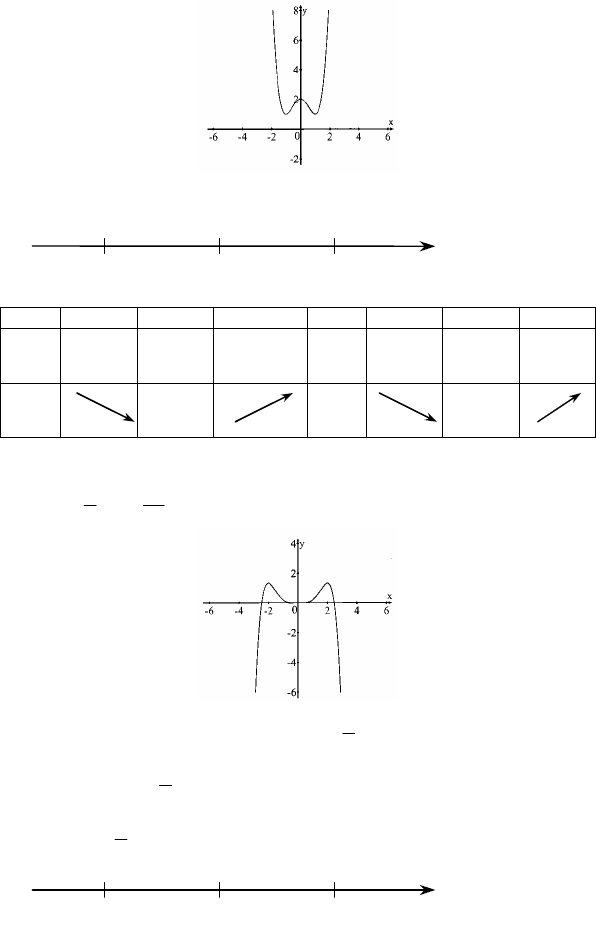
59
1. область определения – R; 2. y′ = 4x
2
– 4x;
3. y′ = 0; 4x(x
2
– 1) = 0, x = 0, x = ±1; 4. y′ > 0; x(x
2
– 1) > 0
–
+
–1 0 1
–
+
-1 < x < 0, x > 1, y′ < 0; x(x2 – 1) < 0 x < -1 0 < x < 1
X x < -1 -1 -1<x<0 0 0<x<1 1 x>1
f’(x) - 0 + 0 - 0 +
f(x) 1 2 1
x = -1 – точка min, f(-1) = 1 – 2 + 2 = 1; x = 0 – точка max,
f(0) = 0 + 0 + 2 = 2; x = 1 – точка min, f(1) = 1 – 2 + 2 = 1
3)
64
24
1
4
1
xxy ⋅−⋅=
1. Область определения – R; 2.
53
4
1
' xxy −=
;
3. y′ = 0;
0
4
1
1
23
=
⎟
⎠
⎞
⎜
⎝
⎛
− xx , x = 0, x = ±2;
4. y’ > 0;
()
04
4
1
23
>− xx ,
+
–
-2 0 2
–
+
