Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

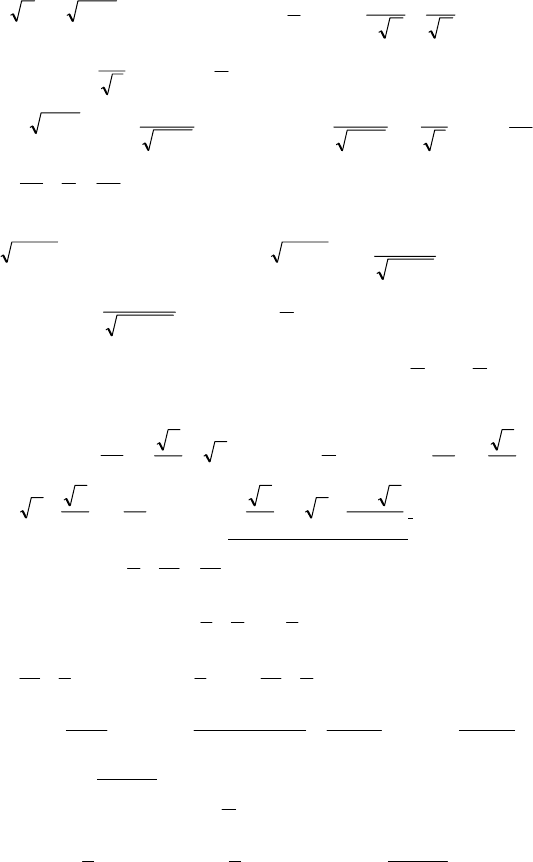
40
x−62=x2 ⇒ x=6–x, 2x=6, x=
2
6
=3, y′=
x
1
x2
12
=
⋅
,
tg α
1
=f ′(x
0
)=
3
1
⇒ α
1
=
6
π
,
y=
x−62 ; y′=
x−
−
6
1
; tg α
2
=f ′(x
0
)=
3
1
36
1
−=
−
−
⇒ α
2
=
6
5π
,
β=
3
2
66
5 π
=
π
−
π
;
2) Точка пересечения графиков:
1+2x =1 ⇒ 2x+1=1 ⇒ x=0, y= 1+2x , y′=
1+2x
1
,
tg α
1
=f ′(x
0
)=
1+02
1
⋅
=1 ⇒ α
1
=
4
π
,
y=1, y′(x)=0, tg α
2
=f ′(x
0
)= 0 ⇒ α
2
=0, β=
4
0
4
π
=−
π
.
№ 889.
1) y(x
0
)=2⋅sin
4
3π
=2⋅
2
2
2
=
, y′(x)=cos
2
x
, y′(x
0
)=cos
2
2
4
3
−=
π
,
y=
⎟
⎠
⎞
⎜
⎝
⎛
π
−
2
3
-x
2
2
2
, y=
4
23
2+x
2
2 ⋅π
+−
;
2) y(x
0
)=2
–2
–2
–4
=
16
3
16
1
4
1
=−
, y′(x)= –2
–x
ln2+2⋅2
–2x
ln2,
y′(x
0
)=ln2⋅(2⋅2
–4
–2
–2
)=ln2
8
1
4
1
8
1
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
ln2,
y=
8
1
16
3
−
ln2(x–2), y=
8
1
−
ln2⋅x+
4
1
16
3
+
ln2;
3) y(x
0
)=
23
22
−
+
=4, y′(x)=
(
)
(
)
()
()
22
x-3
5
x-3
2+xx-3
=
+
, y′(x
0
)=
()
2
2-3
5
=5,
y=4+5(x–2), y=5x–6;
4) y(x
0
)=e+lne=e+1, y′(x)=1+
x
1
, y′(x
0
)=1+e
–1
,
y=e+1+(1+
e
1
)(x-e), y=(1+
e
1
)x+1–1+e–e, y=
e
1)x+(e
.
№ 890.
y′(x)=x
2
–5x, y
2
′=6,
x
2
–5x=6 ⇒ x
2
–5x–6=0,
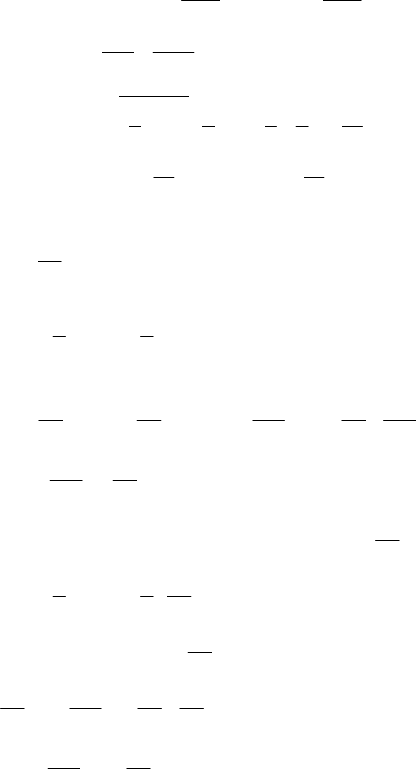
41
D=25+24=49, x
1
=
2
75 +
=6, x
2
=
2
75 −
= –1;
1) x=6, y(6)=
2
365
3
216 ⋅
−
=72–90= –18, y′(6)=36–30=6,
y= –18+6(x–6), y=6x–54;
2) x= –1, y(–1)=
()
6
17
2
5
3
1
1
2
5
1
3
1
−=−−=⋅−−⋅
,
y′(–1)=1+5=6, y=
6
17
−
+6(x+1), y=6x+
6
19
.
№ 891.
y′=
2
x
4
−
, y(1)=4, y′(1)= –4, y=4–4(x–1), y= –4x+8.
Касательная пересекается с осями в точках А (0,8) и В(2,0).
S
∆AOB
=
2
1
OB⋅OA=
2
1
⋅8⋅2=8 (кв. ед.).
№ 892.
y′=
2
x
k
−
, y(x
0
)=
0
x
k
, y′(x
0
)=
2
0
x
k
−
, y
кас
=
2
0
0
x
k
x
k
−
(x–x
0
),
y
кас
=
0
2
0
x
2k
x
x
k
+−
;
1) Точки пересечения с осями координат: А (0,
0
x
2k
), В(2х
0
,0),
S
∆AOB
=
2
1
АО⋅OB=
2
1
⋅
0
x
2k
⋅2х
0
=2k – не зависит от х
0
;
2) Подставим точки (х
0
,
0
x
k
) и (2х
0
, 0) в уравнение касательной
0
x
k
=у=–
2
0
x
k
⋅х
0
+
0
x
2k
=
0
x
k
– подходит, значит, принадлежит касательной
0=у=–
2
0
x
k
⋅2х
0
+
0
x
2k
=0 – подходит, значит, эта точка принадлежит каса-
тельной.
№ 893.
y(1)=1–p y′(x)=3x
2
–p, y′(1)=3–p, y=1–p+(3–p)(x–1),
y=(3–p)x+1–p–3+p, y=(3–p)x–2.
Координаты точки М должны удовлетворять этому уравнению.

42
3=(3–p)=2–2 ⇒ 3–p=
2
5
⇒ p=
2
1
.
№ 894.
y′= =
⋅−
=
−
4ln
4ln24ln4
4ln
2ln24ln4
2
1
1+xx
1+xx
2
2x
–2
x
y′=2, т.е. 2
2x
–2
x
=2, 2
2x
–2
x
–2=0 — это квадратное уравнение относи-
тельно 2
х
D=1+8=9, 2
х
=
2
31 +
=2
1
, х=1; 2
х
=
2
31 −
–1<0 – нет корней;
у(1)=
4ln
24
21
−
=0.
Ответ: искомая точка (1,0).
№ 895.
y′=ln x +1, x>0, y′=0, ln x +1=0 ⇒ ln x = –1 ⇒ x=e
–1
,
y(e
–1
)=
e
1
e
1
e
ln
e
1
−=
−
= .
Расстояние от касательной до оси абцисс: l =0–y=0+
e
1
=
e
1
.
№ 896.
Пусть х
0
– точка касания, тогда у(x
0
)=1+lnx
0
, y′(x)=
x
1
, y′(x
0
)=
0
x
1
,
y=1+lnx
0
+
0
x
1
(x–x
0
), y=
0
x
x
+1+ln x
0
–1, y=
0
x
x
+lnx
0
.
Учитывая, что у=ах–2, получаем систему:
⎩
⎨
⎧
=
⇒
⎪
⎩
⎪
⎨
⎧
2
2-
0
0
0
e=a
ex
lnx=2-
x
1
=a
.
Ответ: а = е
2
.
№ 897.
Пусть х
1
– точка касания графика функции f(x), тогда
f(x
1
)=x
1
2
–4x
1
+3, f ′(x)=2x–4, f ′(x
1
)=2x
1
–4,
y=x
1
2
–4x
1
+3+(2x
1
–4)(x–x
1
),
y=(2x
1
–4)(x)+x
1
2
–4x
1
+3–2x
1
2
+4x
1
y=(2x
1
–4)x+(3–x
1
2
).
Пусть х
2
– точка касания графика функции g(x)
g(x
2
)= –x
2
2
–+6x
2
–10, g ′(x)= –2x+6, g ′(x
2
)= –2x
2
+6,
y= –x
2
2
+6x
2
–10+(6–2x
2
)(x–x
2
)
y=(6–2x
2
)x–x
2
+6x
2
–10–6x
2
+2x
2
2
y=(6–2x
2
)x+(x
2
2
–10)
Т.к. это одна и та же касательная, то

43
x5x
x310x
x264x2
x310x
21
2
1
2
2
21
2
1
2
2
⇒
⎩
⎨
⎧
−=
−=−
⇒
⎩
⎨
⎧
−=−
−=−
⎩
⎨
⎧
=+−
−=
⇒
⎩
⎨
⎧
−+−=−
−=
012x10x
x5x
xx1025310x
x5x
2
2
2
21
2
22
2
2
21
x
2
2
–5x
2
+6=0, D=25–24=1, x
2
=
2
15 ±
=3, x
2
=2; x
2
=3,
y= –1 и y= –6+2x – две общие касательные.
№ 898.
Пусть х
1
– точка касания, тогда y(x
1
)=x
1
3
–6, y′(x)=3x
2
, y′(x
1
)=3x
1
2
,
y= x
1
3
–6+3x
1
2
(x–x
1
), y=3x
1
2
⋅x+(–2x
1
3
–6).
Точки пересечения с осями координат: А(0, –2x
1
3
–6), В (
(
)
2
1
3
1
x
3x
3
2 +
, 0),
S
∆AOB
=
2
1
⋅(–2x
1
3
–6)⋅
(
)
2
1
3
1
x
3x
3
2
+
= –
2
1
›3
2
(х
1
3
+3)
2
.
Но те же рассуждения можно провести для х
2
– второй точки касания.
y=3x
2
2
⋅x+(–2x
2
3
–6), S
COD
=
2
2
›3
2
−
(х
2
3
+3)
2
.
Эти касательные параллельны, так что коэффициенты при х должны
быть равны, т.е. 3x
1
2
=3x
2
2
, x
1
2
=x
2
2
либо x
1
=x
2
– тогда точки совпадают, но у нас две разные прямые
либо x
1
= –x
2
4S
AOB
= S
COD
⎪
⎩
⎪
⎨
⎧
−=
+−=+
⋅−
21
2
3
2
2
2
3
1
2
1
3)(x
3
2
3)(x
3
24
xx
xx
4(х
1
3
+3)
2
=(–х
1
3
+3)
2
, 4х
1
6
+24х
1
3
+36=9–6х
1
3
+х
1
6
3х
1
6
+30х
1
3
+27=0, х
1
6
+10х
1
3
+9=0
4
D
=25–9=16, х
1
3
= –5+4= –1, х
1
= –1, х
1
3
= –5–4= –9, х
1
=
3
9− ,
S
AOB
=
()
3
8
3
8
31
13
2
2
=−=+−
⋅
− ,
S
AOB
=
()
33
2
3
2
3
8
39
362
39
93
2
=
⋅
=+−⋅
⋅
−
.

44
IX глава. Применение производной
и исследованию функций
§ 49 Возрастание и убывание функции
№ 899.
f ′(x)=2x–
2
x
2
, x≠0, f ′(x)>0, 2(x–
2
x
1
)>0, x
2
>0,
x
3
–1>0, x
3
>1, x>1 – возрастает; f ′(x)<0, x<0, 0<x<1 – убывает;
0
x
+
–
1
–
№ 900.
1) y′=2x–1, y’>0, 2x–1>0, >
1
2
– возрастает; y′<0, 2x–1<0, x<
2
1
– убыва-
ет;
2)y′=10x–3, y′>0, 10x–3>0, x>
10
3
– возрастает;
y′<0, 10x–3<0, x<
10
3
– убывает;
3) y
′=2x+2, y′>0, 2x+2>0, x>–1 – возрастает;
y
′<0, 2x+2<0, x<–1 – убывает;
4) y
′=2x+12, y′>0, 2x+12>0, x>–6 – возрастает;
y
′<0, 2x+12<0, x<–6 – убывает;
5) y
′=3x
2
–3, y′>0, 3x
2
–3>0, x
2
>1, x<–1, x>1 – возрастает;
y
′<0, 3x
2
–3<0, x
2
<1, –1<x<1 – убывает;
6) y
′=4x
3
–4x, y′>0, 4x(x
2
–1)>0 при –1<x<0, x>1 – возрастает;
y
′<0, 4x(x
2
–1)<0 при x<–1, 0<x<1 – убывает;
0
x
+
–
1
–
–
1
+
7) y
′=6x
2
–6x–36, y′>0, x
2
–x–6>0.
Решим уравнение x
2
–x–6=0: D=1+24=25, x
1
=
15
2
+
=3, x
2
=
15
2
−
= –2.
при x<–2, x>3 – возрастает; y
′<0 при –2<x<3 – убывает;
–
2
x
+
–
3
+
8) y
′=3x
2
–12x, y′>0 3x(x–4)>0 при x<0, x>4 –возрастает;
y
′<0 при 0<x<4 – убывает;

45
0
x
+
–
4
+
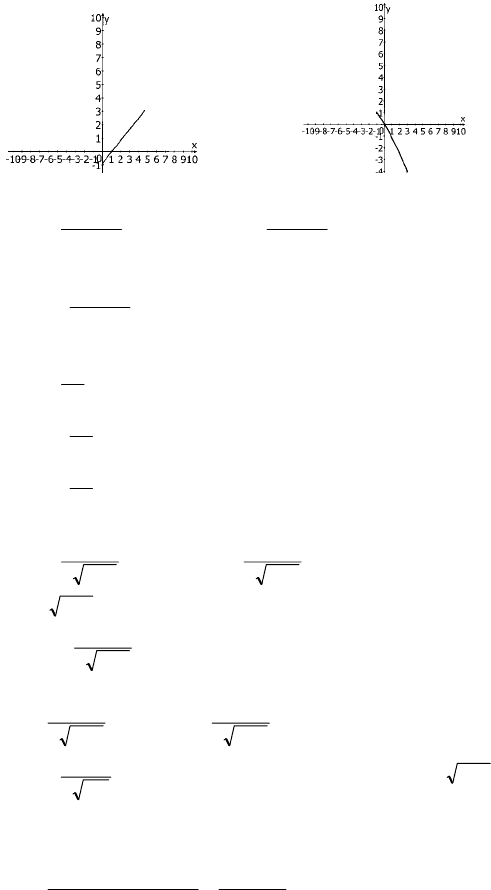
46
№ 901.
а) б)
№ 902.
1) y′= –
2
2)(x
1
+
x≠–2, y′>0: –
2
2)(x
1
+
>0 – не выполняется ни при
каких x∈R, т.к. (x+2)
2
>0,
y′<0: –
2
2)(x
1
+
<0 выполняется при всех x∈R, исключая х= –2
функция убывает при x<–2, x>–2
2) y′= –
2
x
2
, x≠0,
y′>0, –
2
x
2
>0 не выполняется ни при каких x∈R, т.к. x
2
>0,
y′<0, –
2
x
2
<0 выполняется при всех x∈R, исключая х=0,
функция убывает при x<0, x>0
3) y′=
3-x2
1
− , x>3, y′>0:
3-x2
1
− >0 не выполняется ни при каких
x∈R, т.к.
3-x>0;
y
′<0:
3-x2
1
− <0 выполняется при всех x>3,
функция убывает при x>3;
4) y
′=
5-x2
3
, x>5, y
′>0:
5-x2
3
>0 выполняется при всех x>5,
y
′<0:
52
3
x-
<0 не выполняется ни при каких x∈R, т.к. 5-x>0
функция возрастает при x>5.
№ 903.
1) y′=
() ()
2
2
24
2
2
322
3x
9xx
3x
2x3)(x3x
+
+
=
+
⋅−+
x
,

47
y
′>0:
()
2
2
24
3x
9xx
+
+
>0 верно при всех х∈R;
y
′<0:
()
2
2
24
3x
9xx
+
+
<0 не верно ни при каких х∈R.
Функция возрастает при всех х
∈R.
2) y
′=
33222
2
x
10x32
x
32
x
10
x
16
x
10
1
x
1610xx-
−
=+−=
′
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
;
0
x
–
+
3,2
–
y
′>0 при х
3
(32–10х)>0, 0<x<3,2 – возрастает; y′>0, x<0, x>3,2 – убывает.
3) y
′=e
3x
+3e
3x
(x–1)=3e
3x
⋅x–2e
3x
(3x–2),
y
′>0: e
3x
(3x–2)>0 ⇒ e
3x
>0 и 3x–2>0 ⇒ при x>
3
2
функция возрастает;
y
′<0: e
3x
(3x–2)<0 ⇒ e
3x
>0 и 3x–2<0 ⇒ при x<
3
2
функция убывает;
4) y
′=e
–3x
–3xe
–3x
=e
–3x
⋅(1–3x)
y
′>0: e
–3x
(1–3x)>0 ⇒ e
–3x
>0 и 1–3x>0⇒ при x<
3
1
функция возрастает
y
′<0: e
–3x
(1+3x)<0⇒e
–3x
>0 и (1–3x)<0⇒ при x>
3
1
функция убывает.
№ 904.
1) y′=(2x+3)
e
x
2
3x+
;
y
′>0: 2x+3) e
x
2
3x+
>0 ⇒ e
x
2
3x+
>0 и 2x+3>0 ⇒ при x>
2
3
− – функция
возрастает;
y′<0: (2x+3)
e
x
2
3x+
<0 ⇒
e
x
2
3x+
>0 и 2x+3<0⇒ при x<
2
3
−
– функция
убывает;
2) y′=(2x–1)
3
x
2
x−
ln3;
y′>0: (2x–1)
3
x
2
x−
⋅ln3>0 ⇒ 3
x
2
x−
ln3>0 и 2x–1>0 ⇒ при x>
2
1
– функ-
ция возрастает;
y′<0: (2x–1)
3
x
2
x−
⋅ln3<0 ⇒
3
x
2
x−
ln3>0 и 2x–1<0 ⇒ при x>
2
1
– функ-
ция убывает.
№ 905.
1) y′=1–2cos 2x, y′>0: 1–2cos 2x>0 ⇒ cos 2x<
2
1
,
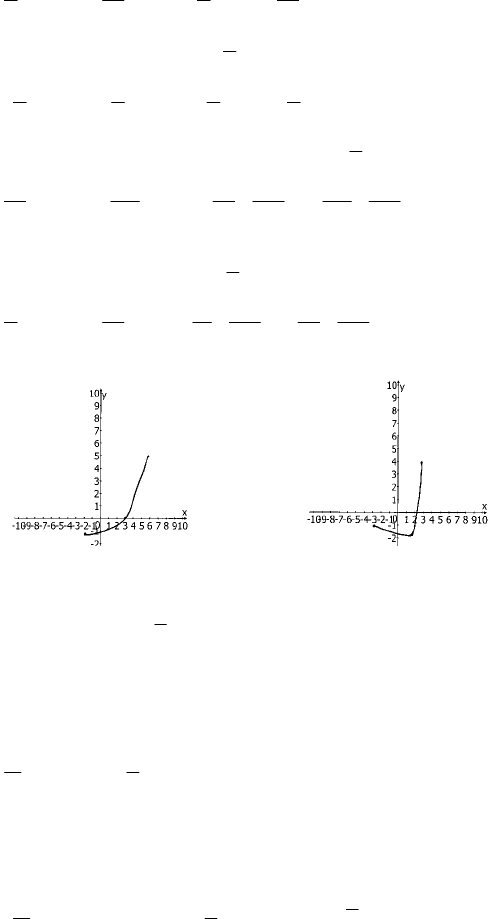
48
3
π
+2πn<2x<
3
5π
+2πn ⇒
6
π
+πn<x<
6
5π
+πn, n∈Z – функция возрастает;
y′<0: 1–2cos 2x<0 ⇒ cos 2x>
1
2
,
–
3
π
+2πn<2x<
3
π
+2πn ⇒ –
6
π
+πn<x<
6
π
+πn, n∈Z – функция убывает;
2) y′=3–6sin3x, y′>0: 3–6sin3x>0 ⇒ sin 3x<
2
1
;
6
5π
+2πn<3x<
6
13π
+2πn ⇒
3
2
18
5 nπ
+
π
<x<
3
2
18
13 nπ
+
π
, n∈Z – функция
возрастает;
y′<0: 3–6sin3x<0 ⇒ sin 3x>
2
1
;
6
π
+2πn<3x<
6
5π
+2πn ⇒
3
2
18
nπ
+
π
<x<
3
2
18
5 nπ
+
π
– функция убывает
№ 906.
№ 907.
1) y′= 3x
2
–a возрастает, значит у′>0 при всех x∈R
y′>0, 3x
2
–a>0, x
2
>
3
a
, a<0;
2) y′=a–cos x, y′>0, a–cos x>0, cos x <a, a>1.
№ 908.
y′=3x
2
–4x+a функция возрастает на R, если y′>0 при всех х
3x
2
–4x+a>0 неравенство выполняется при любых х, если
4
D
=4–3а<0, a>
3
4
. (Опечатка в ответе задачника).
№ 909.
y′=3ax
2
+6x–2 функция убывает на R, если y′<0 при всех х
3ax
2
+6x–2<0 неравенство выполняется при любых х, если
⎪
⎩
⎪
⎨
⎧
⎪
⎩
⎪
⎨
⎧
−<+=
<
2
3
<a
0<a
06a9
4
D
03a
отсюда а<
2
3
− .
49
§ 50 Экстремумы функции
№ 910.
.3,2;5,5
2121
minminmaxmax
=−==−= xxxx
№ 911.
x
1
= –7, x
2
= –4, x
3
= –3, x
4
= –2, x
5
= –1, x
6
=1, x
7
=3, x
8
=4.
№ 912.
1) y′=
2
x
8
2
1
x
8
2
x
−=
′
⎟
⎠
⎞
⎜
⎝
⎛
+ , y′=
2
x
8
2
1
− =0 ⇒
2
1
x
8
2
= ⇒ x
2
=16 ⇒ x
1,2
=±4;
2) y′=6x
2
–30x+36, y′=0 ⇒ 6(x
2
–5x+6)=0,
D=25–24=1, x
1
=
2
15 +
=3, x
2
=
2
15 −
=2;
3) y′=2e
2x
–2e
x
, y′=0, 2e
x
(e
x
–1)=0⇒2e
x
>0 и e
x
–1=0 ⇒ e
x
=1 ⇒ e
x
=e
0
⇒ x=0.
4) y′=cos x +sin x, y′=0 ⇒ cos x +sin x=0,
2 (cos x
2
2
+sin х
2
2
)=0
⇒ 2 cos (x–
4
π
)=0,
x–
π
4
=
π
2
+πn, n∈Z, x=
3
4
π
+πn, n∈Z.
№ 913.
1) y′=
2
22
x
x
x
−=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
+1,
2
2
x
=1, x
2
=2 ⇒ x=± 2 ;
2) y
′=
2
2x
3
2
1
2x
3
2
x
−=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
, y′=0 ⇒
2
2x
3
2
1
=
⇒ x
2
=3 ⇒ x=± 3 ;
3) y
′=2x⋅ е
х
2
1−
, y′=0 ⇒ 2x⋅ е
х
2
1−
=0 ⇒ е
х
2
1−
>0 и 2x=0 ⇒ x=0;
4) y
′= 2
хх
2
+
⋅ln 2⋅(2x+1),
y
′=0 ⇒ 2
хх
2
+
⋅ln 2⋅(2x+1)=0 ⇒ 2
хх
2
+
⋅ln 2>0 и 2x+1=0, x= −
1
2
.
№ 914.
1) y′=4x–20 y′=0 при х=5 – ста-
ционарная точка. При переходе через х=5 у
′
меняет знак с ‘–’ на ‘+‘.
х=5 – точка минимума
2) y
′=6x+36 y′=0 при х= –6
При переходе через х= –6 у
′ меняет знак
с ‘–’ на ‘+‘.
Следовательно х= –6 – точка минимума
x
–
+
5
x
–
+
–
6
