Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

60
x < -2, 0 < x < 2, y′ < 0;
(
)
04
4
1
23
<− xx
, -2 < x < 0, x > 2;
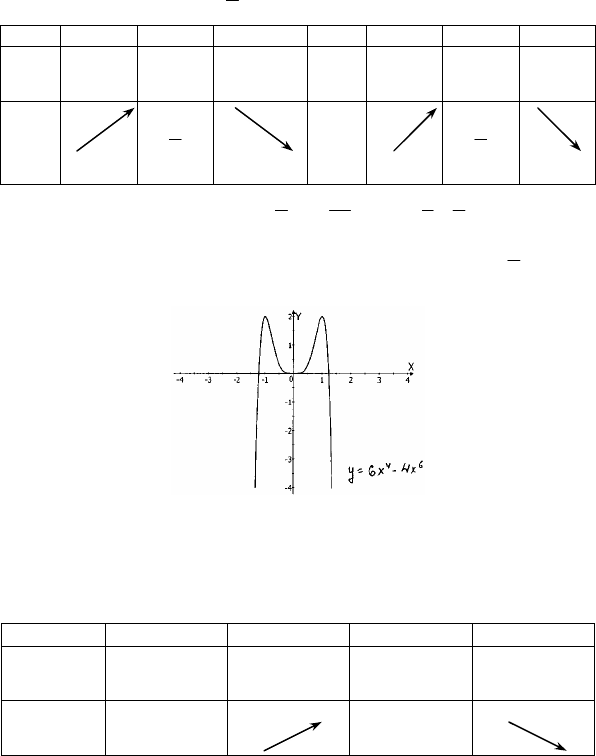
X x < -2 -2 -2<x<0 0 0<x<2 2 x>2
f’(x) + 0 - 0 + 0 -
f(x)
3
4
0
3
4
5. х = -2 – точка max;
()
3
4
3
8
464
24
1
16
4
1
2 =−=⋅−⋅=−f
,
x = 0 - точка min; f(0) = 0 + 0 = 0, x = 2 – точка max;
()
3
4
2 =f
;
4) y = 6x
4
– 4x
6
1. Область определения – R
2. y(-x) = 6(-x)
4
– 4(-x)
6
= 6x
4
– 4x
6
= y(x) – четная, график симметричен
относительно 0у. Исследуем на (0; +∞)
3. y′ = 24x
3
– 24x
5
4. y’ = 0, 24x
3
(1 – x
2
) = 0, x = 0, x = ±1
5.
x 0 (0, 1) 1
(1; +∞)
f’(x) 0 + 0 -
f(x) 0 2
x = 0 – точка min f(0) = 0
x = ±1 – точка max f(1) = f(-1) = 6 – 4 = 2
№ 928
1) у = х
3
– 3х
2
+ 2
1. Область определения [-1; 3] – по условию
2. y′ = 3x
2
– 6x
3. y′ = 0; 3x
2
– 6x = 0, 3x(x – 2) = 0, x = 0, x = 2
4.
61
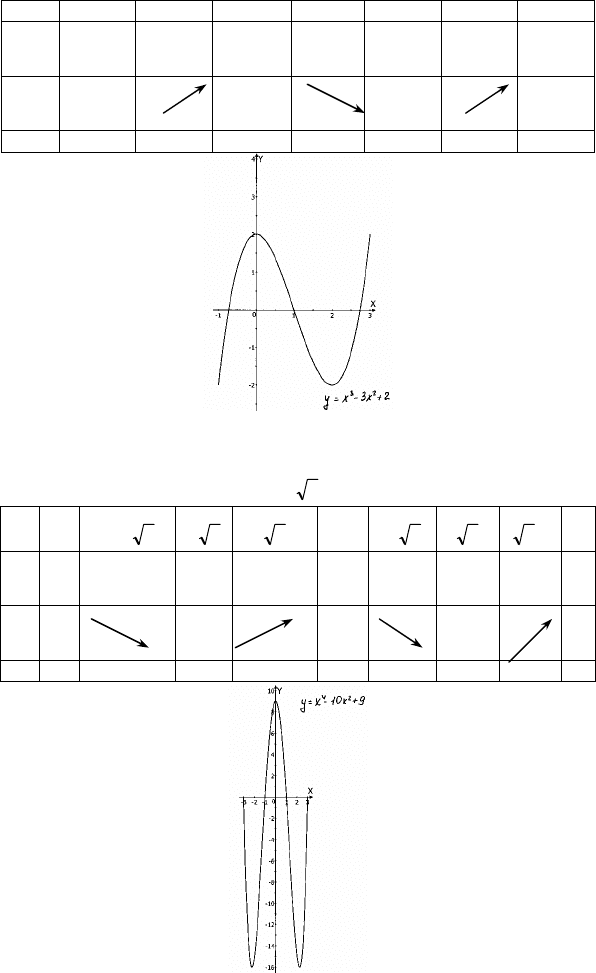
X -1 (-1; 0) 0 (0; 2) 2 (2; 3) 3
y’ + + 0 - 0 + +
y -2 2 -2 2
max min
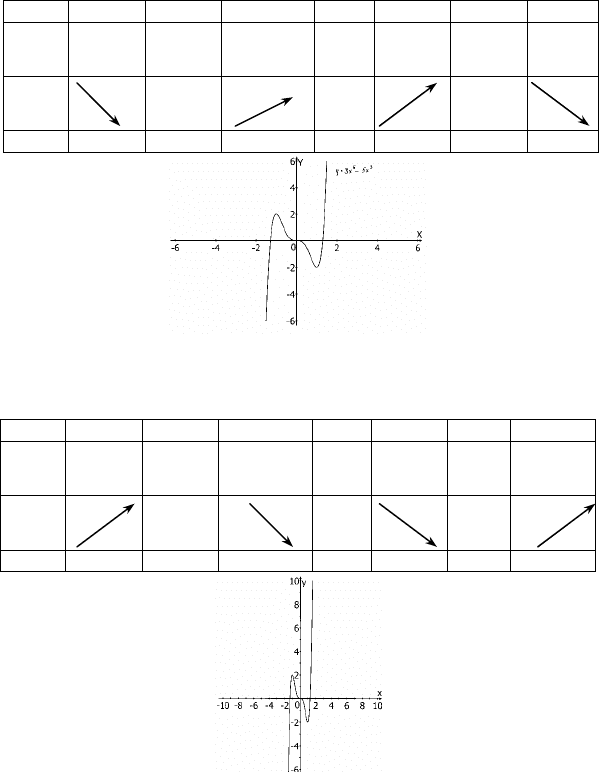
2) y = x4 – 10x + 9 на [-3, 3];
1. Область определения [-3, 3];
2. y′ = 4x
3
– 20x;
3. y′ = 4x(x
2
– 5) = 0, x = 0, x = 5± ;
x -3
(-3;
5−
)
5−
(
)
0;5−
0
(
)
5;0 5
(
)
3;5
3
y’ - 0 + 0 - 0 +
y 0 -16 9 -16 0
min max min
62
№ 929
x
max
= -3, 4; x
min
= -6, 1, 6.
№ 930
1) у = 2 + 5х
3
– 3х
5
1. Область определения – R
2. y′ = 15x
2
– 15x
4
y′ = 0; 15x
2
(1 – x
2
) = 0, x = 0, x = ±1
X x<-1 -1 -1<x<0 0 0<x<1 1 x>1
y’ - 0 + 0 + 0 -
y 0 2 4
min max
2) у = 3х
5
– 5х
3
1. Область определения – IR
2. y′ = 15x
4
– 15x
2
y′ = 0; 15x
2
(x
2
– 1) = 0, x = 0, x = ±1
X x<-1 -1 -1<x<0 0 0<x<1 1 x>1
y’ + 0 - 0 - 0 +
y 2 0 -2
max min
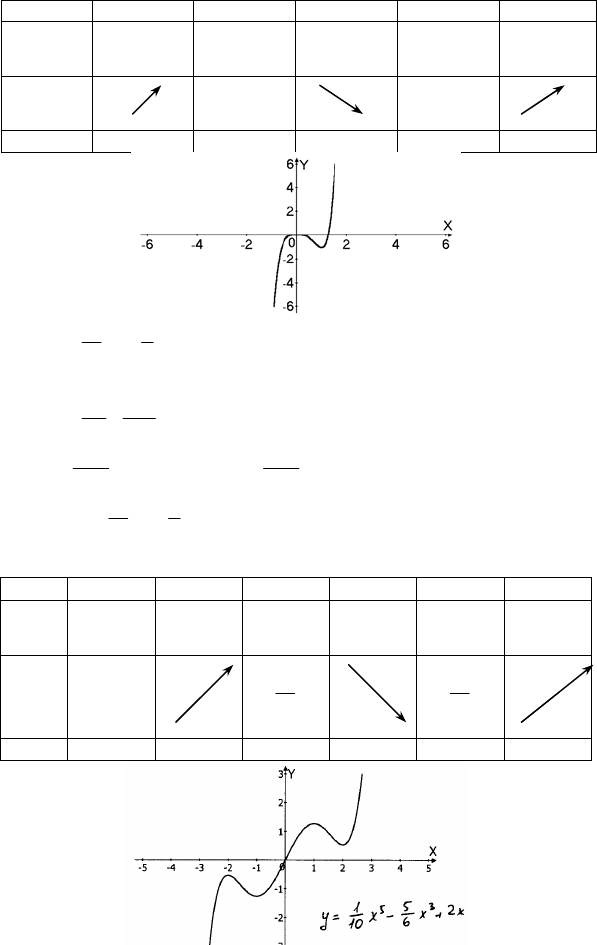
3) y = 4x
5
– 5x
4
1. Область определения – IR; 2. y' = 20x
4
– 20x
3
63
y′ = 0; 20x3(x – 1) = 0, x = 0, x = 1
x x < 0 0 0 < x < 8 1 x > 1
y’ + 0 - 0 +
y 0 -1
max min
4)
xxxy 2
6
5
10
1
35
+−=
;
1. Область определения – R;
2.
2
2
5
2
'
24
+−=
xx
y , y′ = 0; x
4
– 5x
2
+ 4 = 0, D = 25 – 16 = 9,
4
2
35
2
=
+
=x
, x = ±2,
1
2
35
2
=
−
=x
, x = ±1,
() ()
xyxxxxy −=−+−=− 2
6
5
10
1
35
- нечетная функция, симметричная
относительно 0. Продолжим рассуждение на (0; +∞)
х 0 (0;1) 1 (1;2) 2
(2;+∞)
y’ 0 + 0 - 0 +
y 0
15
19
15
8
max min
64
№ 931
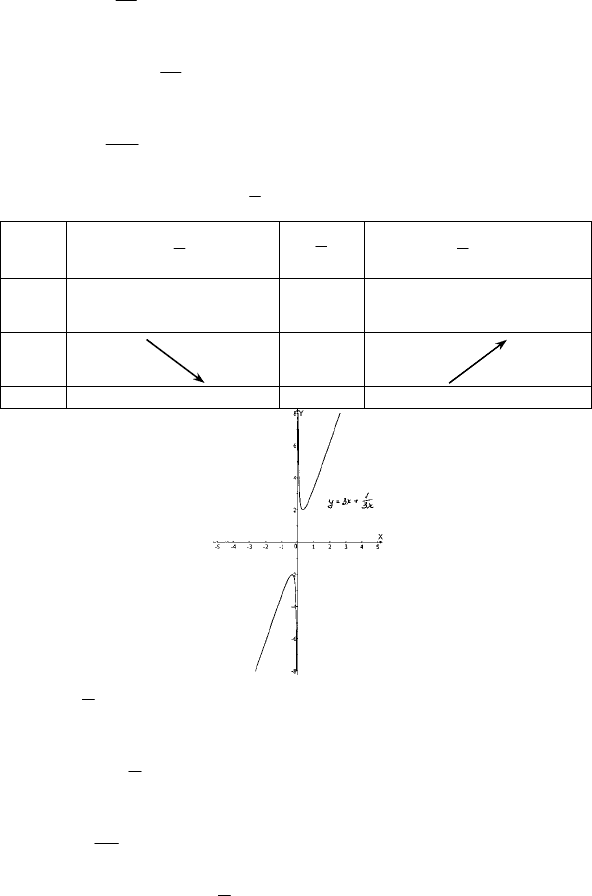
1)
x
xy
3
1
3 += ;
1. Область определения – R при х ≠ 0
2.
() ()
xy
x
xxy −=−−=−
3
1
3 - функция нечетная, график симметричен
относительно 0. Рассмотрим его на (0; +∞)
3.
2
3
1
3'
x
y −=
;
4. y′ = 0; 9x
2
– 1 = 0,
3
1
±=x
;
x
⎟
⎠
⎞
⎜
⎝
⎛
3
1
;0
3
1
⎟
⎠
⎞
⎜
⎝
⎛
+∞;
3
1
y’ - 0 +
y 2
min
2)
x
x
y −=
4
;
1. Область определения х ≠ 0;
2.
() ()
xyx
x
xy −=+−=−
4
- функция нечетна и ее график симметричен
относительно 0. Рассмотрим его на (0; +∞);
3.
1
4
'
2
−−=
x
y ; 4. y′ = 0 4 + x
2
= 0 – не существует стационарных точек;
5. пересечение с 0х:
x
x
−=
4
0
; х
2
= 4, х = ±2;

65
6. если х → ∞, то у → -х, если х → 0, то у → ∞;
7. y > 0,
0
4
0
4
2
>
−
>−
x
x
x
x
при 0 < x < 2;
3)
x
xy
1
−= ;
1. Область определения x > 0; 2.
xx
y
2
1
1' += ;
3. y′ = 0;
012 0
2
1
1 =+=+ xx
xx
,
2
1
3
−=x
— нет стационарных точек;
4. у = 0 при
1 0
1
3
==− x
x
x , х = 1;
5. если х → 0, то у → -∞, если х → ∞, то у → х;
6. y > 0;
1 0
1
3
>>− x
x
x , x > 1;
№ 932
1) у = хе
-х
1. Область определения R; 2. y′ = e
-x
– xe
-x
= e
-x
(1 – x);
66
3. y′ = 0; e
-x
(1 – x) = 0, e
-x
> 0, x = 1, y′ > 0; 1 – x > 0, x < 1;
X x < 1 1 x > 1
y’ + 0 -
Y
e
1
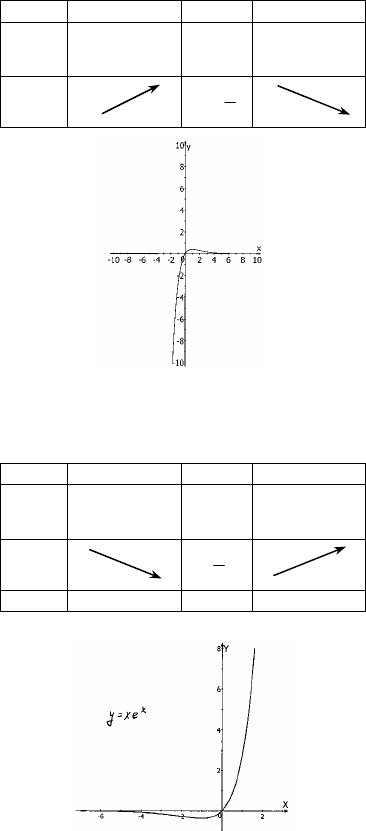
2) y = xe
x
1. Область определения R;
2. y′ = e
x
+ xe
x
= e
x
(1 + x);
3. y′ = 0; e
x
(1 + x) = 0, x = -1;
X x < -1 -1 x > -1
y’ - 0 +
Y
-
e
1
min
x = -1 – точка минимума;
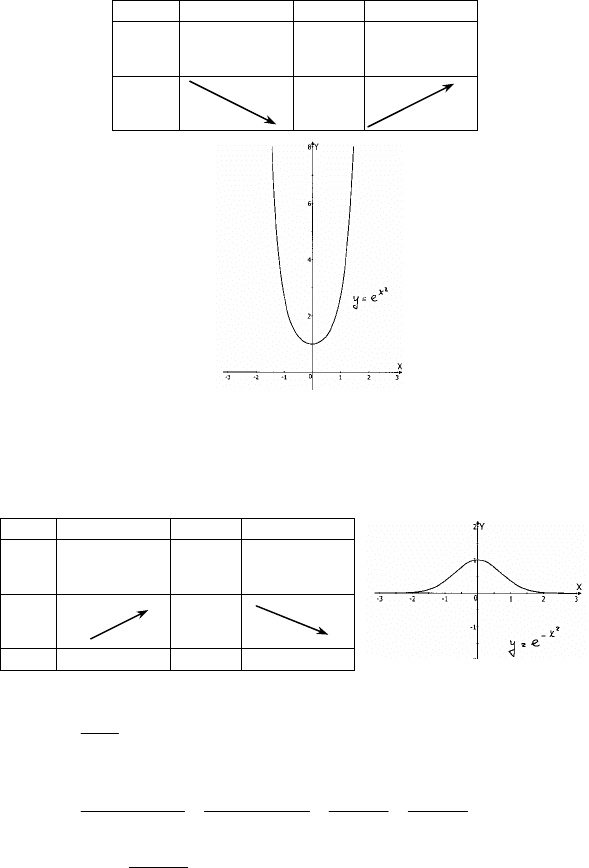
3)
2
x
ey =
;
1. Область определения R:
2.
2
2'
x
xey = ; 3. y′ = 0; 02
2
=
x
xe , x = 0;
67
X x < 0 0 x > 0
y’ - 0 +
Y 1
4)
2
x
ey
−
=
1. Область определения – R:
2.
2
2'
x
exy ⋅−=
3. y′ = 0; 02
2
=⋅−
x
ex , x = 0
X x < 0 0 x > 0
y’ + 0 -
Y 1
max
№ 933
1)
2
2
−
=
x
x
y
1. Область определения: х ≠ 2
2.
()
()
() ()
(
)
()
22
2
2
22
2
2
2
4
2
4
2
42
2
22
'
−
−
=
−
−
=
−
−−
=
−
−−
=
x
xx
x
xx
x
xxx
x
xxx
y
3. y′ = 0 при
()
()
0
2
4
2
=
−
−
x
xx
, х = 0, х = 4
68
1)
X
(-∞;0)
0 (0;2) 2 (2;4) 4
(4;+∞)
y’ + 0 - - 0 +
Y 0 8
max min
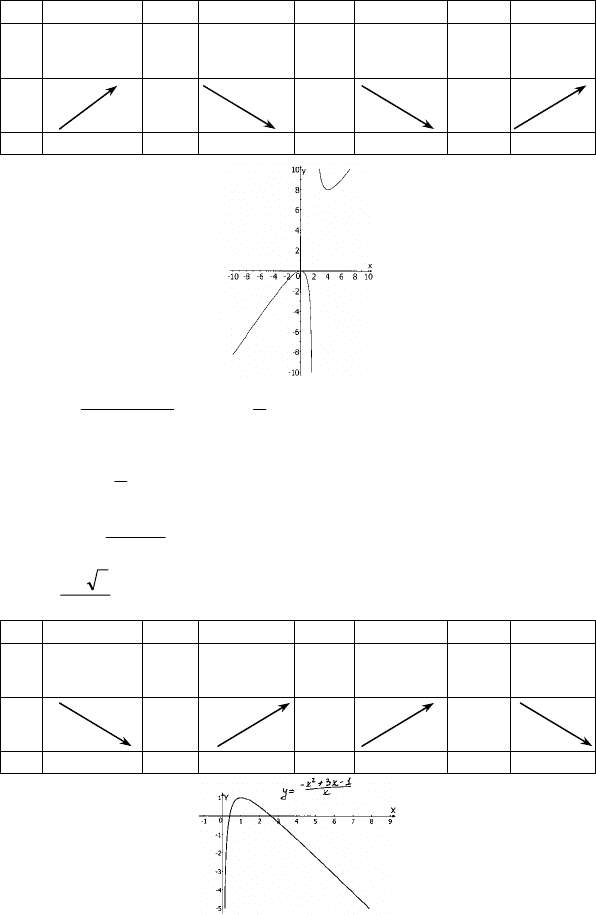
2)
x
x
x
xx
y
1
3
13
2
−+−=
−+−
=
;
1. Область определения х ≠ 0;
2.
x
y
1
1' +−= ;
3. y′= 0;
0
1
2
2
=
+−
x
x
, x = ±1, y = 0; x
2
– 3x + 1 = 0, D = 9 – 4 = 5,
2
53 ±
=x
;
X
(-∞;-1)
-1 (-1;0) 0 (0;1) 1
(1;+∞)
y’ - 0 + + 0 -
Y 5 1
min max
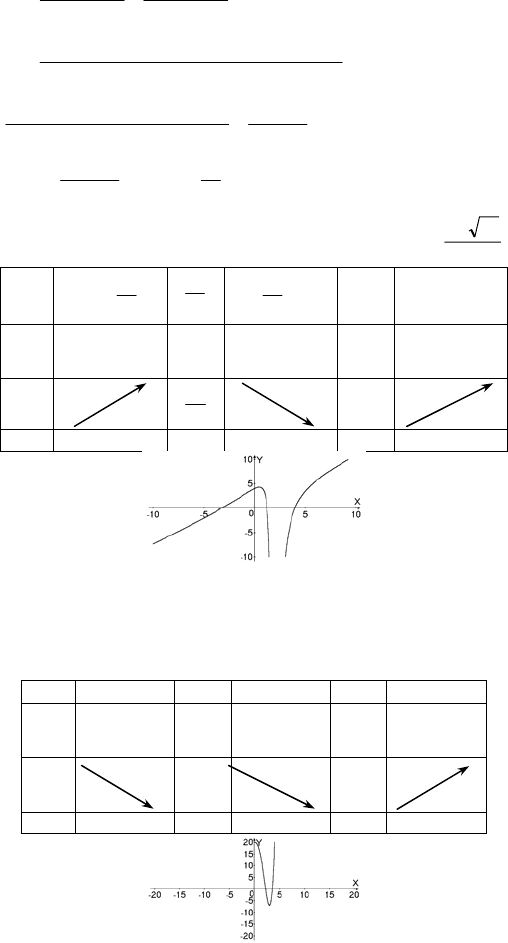
69
3)
()
44
24
2
24
2
2
2
2
+−
−+
=
−
−+
=
xx
xx
x
xx
y
; 1. Область определения х = 2;
2.
()
(
)
(
)
(
)
()
=
−
−+−−+−−
=
4
22
2
24224441
'
x
xxxxxx
y
() ()
33
22
2
107
2
428824
−
−
=
−
+−−+−−
=
x
x
x
xxxxx
;
3. y′ = 0;
()
7
10
0
2
107
3
==
−
−
x
x
x
;
4. y = 0; 4 + x – 2x
2
= 0, 2x
2
– x – 4 = 0, D = 1 + 32 = 33,
4
331±
=x ;
X
⎟
⎠
⎞
⎜
⎝
⎛
∞−
7
10
;
7
10
⎟
⎠
⎞
⎜
⎝
⎛
2;
7
10
2
(2;+∞)
y’ + 0 - +
Y
8
33
max
№ 934
1) Рассмотрим график функции у = х
4
– 4х
3
+ 20. Его пересечение с у = 0
даст количество действительных корней исходного уравнения
1 Область определения R: 2. y′ = 4x
3
– 12x
2
;
3. y′ = 0; 4x
2
(x – 3) = 0, x = 0, x = 3
X
(-∞;0)
0 (0;3) 3
(3;+∞)
y’ - 0 - 0 +
Y 20 -7
min
