Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

21
2)
()
()
=
′
−
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
xsin
xsin3xsin3
xsin
3
2
xxx
(
)
xsin
xcosxsin3ln3
xsin
xcos3xsin3ln3
2
x
2
xx
−⋅
=
−⋅⋅
=
;
3) (ln x⋅cos 3x)′=(ln x)′cos 3x+lnx⋅(cos3x)′=
x
x3cos
+lnx⋅ 3(–sin 3x)=
=
x
x3cos
–3 ln x⋅sin 3x;
4) (log
2
x⋅sin 2x)′=(log
3
x)′sin 2x+log
3
x(sin 2x)′=
=
x2cosxlog2
3lnx
x2sin
x2cos2logx2sin
3lnx
1
33
+=⋅++
.
№ 840.
1) f ′(x)=
()
x
exe
xx
2
2ln2
4242
+=
′
+
−−
, f ′(2)=
2
2
2
422
+
−⋅
e =2+1=3;
2) f ′(x)=
()
()
13
3
313ln
2323
−
−=
′
−−
−−
x
exe
xx
,
f ′(
3
2
)=
13
3
3
3
2
23
3
2
−
−
−⋅
e =3–3=0;
3) f ′(x)=(2
x
–log
2
x)′=2
x
ln2–
2lnx
1
,
f ′(1)= 2
1
ln2–
2ln1
1
⋅
=2 ln2–
2ln
1
=
2ln
12ln2
2
−
;
4) f ′(x)=
()
3ln3
5,0lnx
1
3xlog
xx
5,0
−=
′
− ,
f ′(1)=
3ln3
5,0ln
1
3ln3
5,0ln
1
1
−=−
.
№ 841.
1) f ′(x)=(x–cos x)′=1+sin x, f ′(x)=0 ⇒ 1+sin x=0 ⇒ sin x= –1,
x
2
π
−= +2πn, n∈Z;
2) f ′(x)=(
2
1
x–sin x)′=
2
1
–cos x,
f ′(x)=0 ⇒
2
1
–cos x=0, ⇒ cos x =
2
1
, откуда
х=
3
π
±
+2πn, n∈Z;
21
3) f ′(x)=(2 ln(x+3)–x)′=
3
1
3
32
1
3
2
+
−−
=
+
−−
=−
+ x
x
x
x
x
,
f ′(x)=0 ⇒ –(x+1)=0, ⇒ х= –1;
4) f ′(x)<(ln(x+1)–2x)′=
1
1
+x
–2,
f ′(x)=0 при
1
1
+x
–2=0, т.е. х+1=
2
1
⇒ x= –
2
1
;
5) f ′(x)=(x
2
+2x–12lnx)′=2x+2–
x
12
, f ′(x)=0 ⇒ 2x+2–
x
12
=0 x≠0,
2x
2
+2x–12=0; x
2
+x–6=0, D=1+24=25, х
1
=
2
51+−
=2, х
2
=
2
51 −−
= –3.
Т.к. x>0 ⇒ x=2.
6) f ′(x)=(x
2
–6x–8⋅ lnx)′=2x–6–
x
8
, f ′(x)=0 ⇒ 2x–6–
x
8
=0, x≠0,
2x
2
–6x–8=0; х
2
–3х–4=0; D=9+16=25, х
1
=
2
53 +
=4, х
2
=
2
53 −
= –1,
x>0 ⇒ x=4.
№ 842.
1) f ′(x)=(e
x
–x)′=e
x
–1, f ′(x)>0 при e
x
–1>0, т.е. e
x
>1
или e
x
>е
0
, откуда x>0;
2) f ′(x)=(x ln 2–2
x
)′=ln 2–2
x
ln 2,
f ′(x)>0 при ln2(1–2
x
)>0,
т.к. ln 2>0, то 1–2
x
>0 или 2
x
<1,
2
x
<2
0
, откуда x<0;
3) f ′(x)=(e
x
⋅x
2
)′= e
x
⋅x
2
+2xe
x
,
f ′(x)>0 при e
x
(x
2
+2x)>0, e
x
>0, x(x+2)>0
Ответ: x∈(–∞; –2)∪(0;+∞).
4) f ′(x)=
()
x
e
xexe
x
xx
2
+=
′
f ′(x)>0 при
xe
x
(1+
0)
2
1
>
x
),
т.к.
xe
x
>0, то 1+
x2
1
>0
2
1
−>⇒ x
f ′(x)>0 и x >0. Ответ: х > 0.
№ 843.
1)
()
32
2
36
1
325
52
1223
21
5
32
ln
3
12
+
+
−
=
+
⋅
+
−⋅
⋅
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−
x
x
x
x
xx
2)
() ()
()
=
⋅−
−⋅⋅
−
−
−
⋅=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
352
532
12
1
6
1
3
52
ln2
6
1
x
x
xx
x
x
52
10
112
6
−
+
−
− .
x
–
2
0
+
+
–
2
1
−
x
0
+
+
–
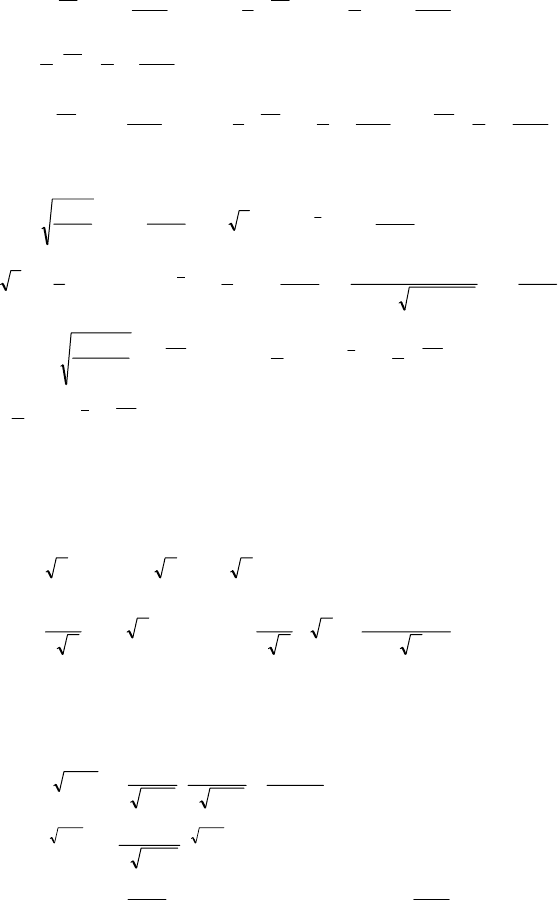
22
3)
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−⋅+
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
′
⎟
⎠
⎞
⎜
⎝
⎛
−
+
−−
2
1
sin
2
1
3
3
1
2
2
1
cos32
3
1
3
1
x
e
x
e
xx
2
1
sin
2
3
3
2
3
1
x
e
x
−
+−=
−
.
4)
=
+
⋅−
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−−
4
1
cos
4
1
2
3
1
3
4
1
sin23
3
2
3
2
x
e
x
e
xx
4
1
cos
2
1
3
2
x
e
x
+
−−
−
.
№ 844.
1)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−−⋅=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
−
3
2
cos323
3
2
cos3
2
3
3
1
3
3
x
x
x
x
()( )
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−⋅−−⋅−⋅
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
−
3
2
sin
3
1
321
3
1
3
3
4
3
x
x
()()
3
2
sin
922
1
3
−
+
⋅−−
x
xx
.
2)
()
()
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅⋅−+
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⋅
−−
−
5
4
4
7
5
4
5
1
52
4
3
25
2
1
2
4
3
xx
exe
x
()
5
4
4
7
2
2
3
−
−+−=
−
x
ex
.
№ 845.
1)
()()
()
=
′
+
′
=
′
⋅ xxx
xxx
2cos5,02cos5,02cos5,0
(
)
=−⋅⋅+= xx
xx
2sin25,02cos5,0ln5,0
(
)
xx
x
2sin22cos5,0ln5,0 − .
2)
()()
(
)
=
⎟
⎠
⎞
⎜
⎝
⎛
′
+
′
=
′
⋅
−−− xxx
exexex 55
(
)
x
xe
x
x
eexe
x
x
xxx
2
215
2
1
5
2
1
5
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−=
−
−−−
.
3) (e
3–2 x
⋅cos(3–2x))′=(e
3–2 x
)′cos(3–2x)+ e
3–2 x
(cos(3–2x))′=
= –2 e
3–2 x
cos (3–2x)–2 e
3–2 x
⋅(–sin(3–2x))=
=–2e
3–2 x
(cos(3–2x)–sin(3–2x)) = 2e
3–2 x
(sin(3–2x)–cos(3–2x)).
№ 846.
1)
()
)1(2
1
12
1
1
1
1ln
−
=
−
⋅
−
=
′
−
x
xx
x .
2)
xx
e
x
e
++
+
=
′
⎟
⎠
⎞
⎜
⎝
⎛
33
32
1
(опечатка в ответе задачника).
3)
()()
⋅=
′
x
x
cos
1
cosln
(–sin x)= –tg x. 4)
()()
⋅=
′
x
x
sin
1
sinln
cos x =ctg x.
23
№ 847.
1)
()
1xcos1xcos
22
++
=
′
⋅ln 2⋅(–sin x). 2)
(
)
xsin1xsin1
5,05,0
++
=
′
⋅ln0,5⋅cos x.
3)
()
()
()
3
2
3
33
23
2sin
2
3
1
2sin2cos
2
3
+
+
−=+⋅+−=
′
+
−
x
x
xxx .
4) (sin (ln x))′=cos(ln x)⋅
x
xcox
x
)(ln1
= .
№ 848.
1)
()
12
1
122
22
12
22
2
−+
+
=
−+
+
=
′
⎟
⎠
⎞
⎜
⎝
⎛
−+
xx
x
xx
x
xx
2)
()
3
2
3
sin3
cos
sin
x
x
x =
′
. 3)
(
)
44
4
cos4
sin
cos4
)sin(1
cos
x
x
x
x
x
−=
−⋅
=
′
.
4)
()
xxxx
x
22
2
log2ln2
1
2lnlog2
1
log
⋅
=
⋅
=
′
№ 849.
1)
()()
=
′
+−
′
+
=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
x
xxxx
x
x
2
sin
)(sincos1sincos1
sin
cos1
()
x
x
x
xxx
x
xxxx
22
22
2
sin
cos1
sin
coscossin
sin
coscos1sinsin +
−=
−−−
=
⋅+−⋅−
=
2)
()
(
)
(
)
()
=
+
′
+−+
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
2
13
133133
13
3
x
xx
x
xxx
(
)
(
)
()
=
+
−+
=
2
32
3
13
3ln3313
x
xx
x
x
()
(
)
()
2
1
2
1332
33ln213
1332
3ln332333
+
+−
=
+
⋅⋅−+⋅
=
+
x
x
x
xx
x
x
x
x
.
3)
()
()()
()
=
−
′
−−−
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
2
5,05,05,0
52cos
52cos52cos
52cos
x
xexe
x
e
xxx
()
()
(
)
()
2
5,0
2
5,05,0
52cos
2sin452cos5,0
52cos
2sin252cos5,0
−
+−
=
−
+−
=
x
xxe
x
xexe
xxx
.
4)
()
()
(
)
()
()
=
+
′
+−+
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
2
222
73sin
73sin573sin5
73sin
5
x
xx
x
xxx
(
)
()
=
+
⋅⋅−+⋅⋅
=
2
22
73sin
3cos3573sin5ln52
x
xx
xx
(
)
()
2
2
73sin
3cos35ln143sin5ln25
+
−+⋅⋅
x
xx
x

24
№ 850.
1)
()
(
)
()
=
′
−−
′
−
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−−−
2
x
xeexee
x
ee
xxxxxx
(
)
(
)
=
+−⋅+⋅
=
⋅−−⋅+
=
−−−−
22
1
x
eexexe
x
eexee
xxxxxxxx
2
)1()1(
x
xexe
xx
++−
;
2)
(
)
(
)
()
=
⋅
′
⋅−−⋅⋅
′
−
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
−
2ln
2lnlog22lnlog2
2ln
log2
22
222
x
xxxx
x
x
xxx
(
)
(
)
=
⋅
⋅−−⋅⋅−
=
22
2
2ln
1
2ln
2lnlog22ln2ln2
x
xx
x
x
x
2ln
log22ln2
22
2
2ln
1
⋅
+−−⋅
x
xx
xx
.
№ 851.
1)
()()()
=
′
⋅−−⋅
′
−
=
′
⎟
⎠
⎞
⎜
⎝
⎛
−
2
cossincossincossin
x
xxxxxx
x
xx
()
(
)
=
⋅−−⋅+
=
2
1cossinsincos
x
xxxxx
22
)1(sin)1(coscossinsincos
x
xxxx
x
xxxxxx −++
=
+−⋅+⋅
=
2)
()
()
x
xx
xx
xx
x
xxx sincoscossin
cossin
cossin
cossin
2sin1
2
+=
′
−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
′
⎟
⎠
⎞
⎜
⎝
⎛
−
−
.
№ 852.
1)
()
()
=
′
+−=
′
xxxxf 5cos2cossin5)(
()
(
)
(
)
=−+=−⋅⋅++= xxxxxx 5sin2sincos55sin52sincos5
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
π
+= xxx 5sin2
2
coscos5
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
π
+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
π
⎟
⎠
⎞
⎜
⎝
⎛
π
+= xxxx 5sin
4
sin255sin2
4
sin
4
sin25
⎟
⎠
⎞
⎜
⎝
⎛
+
π
⎟
⎠
⎞
⎜
⎝
⎛
−
π
=
−+−+
⋅=
ππ
xx
xxxx
3
8
cos2
8
sin210
2
5
cos
2
5
sin225
44
f′(x)=0 при
⎟
⎠
⎞
⎜
⎝
⎛
+
π
⎟
⎠
⎞
⎜
⎝
⎛
−
π
xx 3
8
cos2
8
sin =0,
Откуда:
⎢
⎢
⎢
⎢
⎣
⎡
π
+
π
=
π
+
π
=
⇒
⎢
⎢
⎢
⎢
⎣
⎡
π+
π
=+
π
π=−
π
∈
∈
Zkk
Znn
x
x
kx
nx
,
,
38
216
2
3
8
2
8
25
2)
()()
=
′
−−+−=
′
xxxxxf 2cossin22cos51)((
()
=
−
+
+= 2sincos22sin10 xxx
()
=−++
⎟
⎠
⎞
⎜
⎝
⎛
−
π
2sincos22
2
cos10 xxx
()
=−++
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
π
−
⎟
⎠
⎞
⎜
⎝
⎛
−
π
= 2sincos2
4
sin
4
cos10
22
xxxx
=−
⎟
⎠
⎞
⎜
⎝
⎛
−
π
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
π
= 2
4
cos221
4
cos210
2
xx
12
4
cos22
4
cos20
2
−
⎟
⎠
⎞
⎜
⎝
⎛
−
π
+
⎟
⎠
⎞
⎜
⎝
⎛
−
π
= xx
f ′(x)=0, если
12
4
cos22
4
cos20
2
−
⎟
⎠
⎞
⎜
⎝
⎛
−
π
+
⎟
⎠
⎞
⎜
⎝
⎛
−
π
xx =0
cos(
4
π
–x)=t, 20t
2
+2 2 t–12=0 или 10t
2
+ 2 t–6=0 D=2+240=242=2⋅121
t
1
=
2
2
20
2112
=
+−
t
2
=
5
23
20
2112
−=
−−
1
5
23
2518;1
25
29
;1
5
23
<⇒<∨
⋅
∨
Cледовательно, –
5
23
>–1.
−
π
4
х
1
=±arccos(–
5
23
)+2πn,
n∈Z
Znnx ∈π+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−±
π
=⇒ ,2
5
23
arccos
4
1
−
π
4
x
2
=±
4
π
+2πk, k∈Z ZmmxZkkx ∈π+
π
=∈π=⇒ ,2
2
,,2
32
№ 853.
1)
()
()
(
)
() ()()
=
′
−+−⋅
′
=
′
−=
′
12ln12ln12ln)(
222
xexexexf
xxx
() ()
⎟
⎠
⎞
⎜
⎝
⎛
−
+−=
−
+−=
12
1
12ln2
12
2
12ln2
2
2
2
x
xe
x
e
xe
x
x
x
,
f(x)=0 ⇒ e
2x
ln(2x–1)=0, e
2x
>0, так что ln(2x–1)=0, ln(2x–1)=ln 1;
2x–1=1; x=1, f ′(1)=
()
⎟
⎠
⎞
⎜
⎝
⎛
−⋅
+−⋅
⋅
112
1
112ln2
12
e
=2e
2
⋅(0+1)=2e
2
.
2)
=
′
⎟
⎠
⎞
⎜
⎝
⎛
−
=
′
x
xx
xf
sin
cossin
)(
()()()
=
′
−−
′
−
=
x
xxxxxx
2
sin
sincossinsincossin
26
()
(
)
=
−−+
=
x
xxxxxx
2
sin
coscossinsinsincos
xx
xxxxxx
22
22
sin
1
sin
coscossinsinsincos
=
+−+⋅
=
f(x)=0 ⇒
=
⎟
⎠
⎞
⎜
⎝
⎛
−
x
xx
sin
cossin
0
Область определения функции sin x≠0 x≠πn, n∈Z
1–ctg x=0 ctg x=1 x=
4
π
+πn, n∈Z ;
(
)
2
1
sin
1
4
2
1
4
2
===
⎟
⎠
⎞
⎜
⎝
⎛
π
′
π
f .
Т.к. в f ′(x) sin входит в квадрате, то f ′(x) во всех точках
nπ+
π
4
, будет
иметь одно и то же значение.
№ 854.
f ′(x)=(x sin 2x)′=(x)′sin 2x+x(sin 2x)′=sin 2x+2x cos 2x
y(x)=f ′(x)+f(x)+2=sin 2x+2x cos 2x+x sin 2x+2
y(π)=sin 2π+2π cos 2π+π sin 2π+2=0+2π+0+2=2(1+π).
№ 855.
1) f ′(x)=(x– ln x)=1–
x
1
, x>0
f ′(x)=0 при х=1; f ′(x)>0,
x
x 1−
>0, x(x–1)>0 ⇒ х∈(1;+∞);
f ′(x)<0 при х∈(0;1);
2) f ′(x)=(x lnx)′= lnx+1, x>0
f ′(x)=0, lnx+1=0, lnx = –1,
lnx=lne
–1
, x=e
–1
.
f ′(x)>0, lnx+1>0; lnx>–1=ln e
–1
;
x>e
–1
x∈(e
–1
;+∞); f ′(x)<0 при х∈(0;e
–1
);
3) f ′(x)=(x
2
lnx)′=2xlnx+x x>0
f ′(x)=0 x(2lnx+1)=0 x=0 и lnx=
2
1
−
=ln
2
1
−
e x=
e
1
f ′(x)>0 x(2 ln x+1)>0 при x∈(
e
1
; +∞)
f ′(x)<0 при x∈(0;
e
1
) x>0
+
–
+
0
х
e
1
+
–
+
0
х1
+
–
+
0
х
e
1

27
4) f ′(x)=(x
3
–3 lnx)′=3x
2
–
x
3
f ′(x)=0, 3x
2
–
x
3
=0, 3x
3
–3=0, x
3
=1, x=1; f ′(x)>0, 3x
2
–
x
3
> 0,
x
x 33
3
−
>0
3x(x
3
–1)>0 при х∈(1;+∞);
f ′(x)<0 при х∈(0;1).
+
–
+
0
х
1
№ 856.
При x<2 и x>3 выражение под знаком логарифма положительно
(ln(x
2
–5x+6))′= ⋅
+− 65
1
2
xx
(2x–5).
§ 48 Геометрический смысл производной
№ 857.
1) k=tg α=tg
4
π
=1, x
0
=2 y
0
= –3, т.е. –3=1⋅2+b b= –5;
2) k=tg, α=tg
4
π
=1, x
0
= –3 y
0
=2, т.е. 2=1⋅(–3)+b b=5;
3) k=tg, α=tg
3
3
−=
⎟
⎠
⎞
⎜
⎝
⎛
π
− , x
0
=1, y
0
=1, т.е. 1= – 3 ⋅1+b, b=1+ 3;
4) k=tg, α=tg
3
3
6
−=
⎟
⎠
⎞
⎜
⎝
⎛
π
−
, x
0
=–1, y
0
=–1, т.е. –1=
3
3
−
⋅(–1)+b, b=
3
3
−
–
1
№ 858.
1) f ′(x)=3x
2
; k=tg α =f ′(x
0
)=3⋅1
2
=3;
2) f ′(x)=cos x; k=tg α =f ′(x
0
)=cos
2
2
4
=
π
;
3) f ′(x)=
x
1
; k=tg α =f ′(x
0
)=
1
1
=1;
4) f ′(x)=e
x
; k=tg α =f ′(x
0
)=
3ln
e=3.
№ 859.
1) f ′(x)=x
2
; tg α =f ′(x
0
)=1
2
=1 ⇒ α=
4
π
;
2) f ′(x)= –
2
1
x
; tg α =f ′(x
0
)=
2
1
1
−
= –1 ⇒ α=
4
3π
;
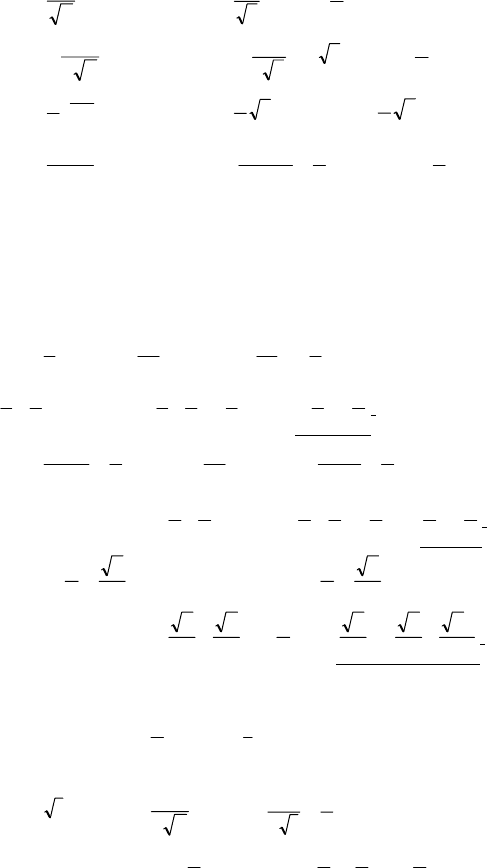
28
3) f ′(x)=
x
1
; tg α =f ′(x
0
)=
3
1
⇒ α=
6
π
;
4) f ′(x)=
xx
9
−
; tg α =f ′(x
0
)=
33
9
− = –
3 ⇒ α=
3
π
−
;
5) f ′(x)=
2
1x3
e
2
3
+
; tg α =f ′(x
0
)= e
2
3
⇒ α=arctg ( e
2
3
);
6) f ′(x)=
12
2
+x
; tg α =f ′(x
0
)=
5
2
122
2
=
+⋅
⇒ α=arctg
5
2
.
№ 860.
1) f(x
0
)=1
2
+1+1=3, f ′(x)=2x+1, f ′(x
0
)=2⋅1+1=3, y=f(x
0
)+ f ′(x
0
)(x–x
0
),
y=3+3(x–1), y=3+3x–3, y=3x;
2) f(x
0
)=2–3⋅2
2
= –10, f ′(x)=1–6x, f ′(x
0
)=1–6⋅2= –11,
y=f(x
0
)+ f ′(x
0
)(x–x
0
),
y= –10–11(x–2), y= –10–11x+22, y=12–11x.
3) f(x
0
)=
3
1
, f ′(x)=
2
1
x
−
, f ′(x
0
)=
9
1
3
1
2
−=− , y=f(x
0
)+ f ′(x
0
)(x–x
0
),
y=
9
1
3
1
−
(x–3) y=
3
1
9
1
3
1
+− x
y=
3
2
9
1
+− x
;
4) f(x
0
)=
()
4
1
2
1
2
=
−
, f ′(x)=
3
2
x
−
, f ′(x
0
)=
4
1
)2(
2
3
=
−
−
,
y=f(x
0
)+ f ′(x
0
)(x–x
0
), y=
4
1
4
1
+
(x+2) y=
2
1
4
1
4
1
++ x
, y=
4
3
4
1
+x
;
5) f(x
0
)=sin
2
2
4
=
π
, f ′(x)=cos x, f ′(x
0
)=cos
2
2
4
=
π
,
y=f(x
0
)+ f ′(x
0
)(x–x
0
), y=
⎟
⎠
⎞
⎜
⎝
⎛
π
−+
42
2
2
2
x , y=
8
2
2
2
2
2 π
−+x
;
6) f(x
0
)=e
0
=1, f ′(x)=e
x
, f ′(x
0
)=e
0
=1, y=f(x
0
)+ f ′(x
0
)(x–x
0
),
y=1+1(x–0), y=x+1;
7) f(x
0
)=ln 1=0, f ′(x)=
x
1
, f ′(x
0
)=
1
1
=1,
y=f(x
0
)+ f ′(x
0
)(x–x
0
), y=0+1(x–1), y=x–1;
8) f(x
0
)= 1=1, f ′(x)=
x2
1
, f ′(x
0
)=
2
1
12
1
= ,
y=f(x
0
)+ f ′(x
0
)(x–x
0
), y=1+
2
1
(x–1), y=1+
2
1
x–
2
1
, y= )1(
2
1
+x .
29
№ 861.
1) f ′(x)>0 ⇒ tg α>0 ⇒ α∈[0;
2
π
], f ′(x)<0 ⇒ tg α<0 ⇒ α∈[–
2
π
; 0],
f ′(x)=0 ⇒ tg α=0 ⇒ α=0;
рис. а; а) f ′(x)>0: A, B, E; б) f ′(x)<0: D, G; в) f ′(x)=0: C, F.
рис. б; а) f ′(x)>0: C, G; б) f ′(x)<0: A, E; в) f ′(x)=0: B, D, F.
№ 862.
1) f(0)=0+
10
1
+
=1, f ′(x)=1–
2
)1(
1
+x
, f ′(0)=1–
2
)10(
1
+
=0,
y=1+0⋅(x–0), y=1.
2) f(0)=sin 0 – ln 1=0
f ′(x)=2cos 2x–
1
1
+x
, f ′(0)= 2cos 0–
1
1
=1,
y=0+1⋅(x–0), y=x.
№ 863.
1) f ′(x)=1–e
x
, f ′(0)=1–e
0
=0, tg α=f ′(x
0
)=0 ⇒ α=0 ⇒ β=90°–α=90°;
2) f ′(x)= –sin x, f ′(0)= – sin 0 = 0, tg α=f ′(x
0
) ⇒ α=0 ⇒ β=90°–α=90°;
3) f ′(x)=
12
1
+x
+0⋅e
2
=
12
1
+x
,
tg α=f ′(x
0
)=
12
1
+x
=
2
1
⇒ α=arctg
2
1
⇒ β=90°–α=90° –arctg
2
1
.
№ 864.
1) а) Абсцисса точки пересечения графиков:
8–x=4
4+x ; 64–16x+x
2
=16x+64; x
2
–32x=0; x(x–32)=0
x
1
=0 x
2
=32 – посторонний корень, т.к. 8 – х ≥ 0; х=0.
б) угол наклона первой касательной в точке х = 0
tg α
1
=f ′(x
0
)=(8–x)′= –1, α
1
=
4
3π
.
в) угол наклона второй касательной:
tg α
2
=f ′(x
0
)=
2
2
4
2
42
4
00
=
+
=
+ xx
=1, α
2
=
4
π
г) β=
4
3π
–
24
π
=
π
2) а) Абсцисса точки пересечения графиков:
2
1
(х+1)
2
=
2
1
(х–1)
2
;
2
1
(x
2
+2x+1–x
2
+2x–1)=0; 2x=0, x=0;
б) угол наклона первой касательной при х = 0:
