Jost J. Partial Differential Equations

Подождите немного. Документ загружается.

3.3 The Alternating Method of H.A. Schwarz 67

We exclude the trivial case ϕ = const. Let u

: Ω

→ R be harmonic with

boundary values

= ϕ

= M. (3.3.1)

Next, let u

: Ω

→ R be harmonic with boundary values

= ϕ

= u

. (3.3.2)

Unless ϕ

≡ M, by the strong maximum principle,

<M in Ω

;

(3.3.3)

hence in particular,

<M, (3.3.4)

and by the strong maximum principle, also

<M in Ω

, (3.3.5)

and thus in particular,

. (3.3.6)

If ϕ

≡ M, then by our assumption that ϕ ≡ const is excluded, ϕ

≡ M,and

(3.3.6) likewise holds by the maximum principle. Since by (3.3.2), u

and u

coincide on the partition of the boundary of Ω

∗

, by the maximum principle

again

in Ω

∗

Inductively, for n ∈ N,let

2n+1

: Ω

→ R,

2n+2

: Ω

→ R,

be harmonic with boundary values

2n+1

= ϕ

2n+1

= u

, (3.3.7)

2n+2

= ϕ

2n+2

= u

2n+1

. (3.3.8)

From repeated application of the strong maximum principle, we obtain

The boundary values here are not continuous as in the maximum principle, but

they can easily be approximated by continuous ones satisfying the same bounds.

This easily implies that the maximum principle continues to hold in the present

situation.

68 3. Existence Techniques I: Methods Based on the Maximum Principle

2n+3

2n+2

2n+1

on Ω

∗

, (3.3.9)

2n+3

2n+1

on Ω

, (3.3.10)

2n+4

2n+2

on Ω

. (3.3.11)

Thus, our sequences of functions are monotonically decreasing. Since they

are also bounded from below by m, they converge to some limit

u : Ω → R.

The Harnack convergence theorem (1.2.10) ) then implies that u is harmonic

on Ω

and Ω

, hence also on Ω = Ω

∪Ω

. This can also be directly deduced

from the maximum principle: For simplicity, we extend u

to all of Ω by

putting

2n+1

:= u

on Ω

\ Ω

∗

2n+2

:= u

2n+1

on Ω

\ Ω

∗

Then u

2n+1

is obtained from u

by harmonic replacement on Ω

, and anal-

ogously, u

2n+2

is obtained from u

2n+1

by harmonic replacement on Ω

.We

write this symbolically as

2n+1

= P

, (3.3.12)

2n+2

= P

2n+1

. (3.3.13)

For example, on Ω

we then have

u = lim

n→∞

= lim

n→∞

. (3.3.14)

By the maximum principle, the uniform convergence of the boundary values

(in order to get this uniform convergence, we may have to restrict ourselves

to an arbitrary subdomain Ω



⊂⊂ Ω

) implies the uniform convergence of

the harmonic extensions. Consequently, the harmonic extension of the limit

of the boundary values equals the limit of the harmonic extensions, i.e.,

lim

n→∞

= lim

n→∞

. (3.3.15)

Equation (3.3.14) thus yields

u = P

u, (3.3.16)

meaning that on Ω

, u coincides with the harmonic extension of its boundary

values, i.e., is harmonic. For the same reason, u is harmonic on Ω

We now assume that the boundary values ϕ are continuous, and that all

boundary points of Ω

and Ω

are regular. Then ﬁrst of all it is easy to

see that u assumes its boundary values ϕ on ∂Ω \(Γ

∩Γ

) continuously. To

verify this, we carry out the same alternating process with harmonic functions

2n−1

: Ω

→ R, v

: Ω

→ R starting with boundary values

3.3 The Alternating Method of H.A. Schwarz 69

= ϕ

= m (3.3.17)

in place of (3.3.1). The resulting sequence (v

)

n∈N

then is monotonically

increasing, and the maximum principle implies

in Ω for all n. (3.3.18)

Since we assume that ∂Ω

and ∂Ω

are regular and ϕ is continuous, u

and

then are continuous at every x ∈ ∂Ω \(Γ

∩Γ

). The monotonicity of the

sequence (u

), the fact that u

(x)=v

(x)=ϕ(x)forx ∈ ∂Ω \(Γ

∩Γ

)for

all n, and (3.3.18) then imply that u = lim

n→∞

at x as well.

The question whether u is continuous at ∂Ω

∩∂Ω

is more diﬃcult, as can

be expected already from the observation that the chosen boundary values

for u

typically are discontinuous there even for continuous ϕ.Inordertobe

able to treat that issue here in an elementary manner, we add the hypotheses

that the boundaries of Ω

and Ω

are of class C

in some neighborhood

of their intersection, and that they intersect at a nonzero angle. Under this

hypotheses, we have the following lemma:

Lemma 3.3.1: There exists some q<1, depending only on Ω

and Ω

,with

the following property: If w :

→ R is harmonic in Ω

, and continuous on

the closure

,andif

w =0 on Γ

|w|≤1 on γ

then

|w|≤q on γ

, (3.3.19)

and a corresponding result holds if the roles of Ω

and Ω

are interchanged.

The proof will be given in Section 3.4 below.

With the help of this lemma we may now modify the alternating method in

such a manner that we also get continuity on ∂Ω

∩ ∂Ω

. For that purpose,

we choose an arbitrary continuous extension ¯ϕ of ϕ to γ

, and in place of

(3.3.1), for u

we require the boundary condition

= ϕ

=¯ϕ, (3.3.20)

and otherwise carry through the same procedure as above. Since the bound-

aries ∂Ω

, ∂Ω

are assumed regular, all u

then are continuous up to the

boundary. We put

2n+1

:= max

2n+1

− u

2n−1

2n+2

:= max

2n+2

− u

70 3. Existence Techniques I: Methods Based on the Maximum Principle

On γ

,wethenhave

2n+2

= u

2n+1

= u

2n−1

hence

2n+2

− u

= u

2n+1

− u

2n−1

and analogously on γ

2n+3

− u

2n+1

= u

2n+2

− u

Thus applying the lemma with w =

2n+3

−u

2n+1

)

2n+2

, we obtain

2n+3

≤ qM

2n+2

and analogously

2n+2

≤ qM

2n+1

Thus M

converges to 0 at least as fast as the geometric series with coeﬃcient

q<1. This implies the uniform convergence of the series

∞



n=1

2n+1

− u

2n−1

) = lim

n→∞

2n+1

, and likewise the uniform convergence of the series

∞



n=1

2n+2

− u

) = lim

n→∞

. The corresponding limits again coincide in Ω

∗

, and they are harmonic

on Ω

, respectively Ω

, so that we again obtain a harmonic function u on Ω.

Since all the u

are continuous up to the boundary and assume the boundary

values given by ϕ on ∂Ω, u then likewise assumes these boundary values

continuously.

We have proved the following theorem:

Theorem 3.3.1: Let Ω

and Ω

be bounded domains all of whose boundary

points are regular for the Dirichlet problem. Suppose that Ω

∩ Ω

= ∅ and

that Ω

and Ω

are of class C

in some neighborhood of ∂Ω

∩∂Ω

, and that

they intersect there at a nonzero angle. Then the Dirichlet problem for the

Laplace equation on Ω := Ω

∪ Ω

is solvable for any continuous boundary

values.



3.4 Boundary Regularity 71

3.4 Boundary Regularity

Our ﬁrst task is to present the proof of Lemma 3.3.1:

In the sequel, with r := |x − y| = 0, we put

Φ(r):=−dw

Γ (r)=



for d =2,

d−2

for d ≥ 3.

(3.4.1)

We then have for all ν ∈ R

∂

∂ν

Φ(r)=∇Φ · ν = −

(x − y) · ν. (3.4.2)

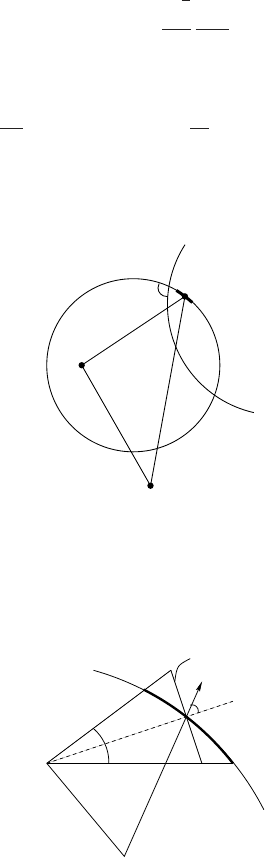
We consider the situation depicted in Figure 3.3.

dγ

(y)

Figure 3.3.

That is, x ∈ Ω

; y ∈ γ

, α =0,π,∂Ω

,∂Ω

∈ C

.Letdγ

(y) be an inﬁnites-

imal boundary portion of γ

(see Figure 3.4).

dω

dγ

(y)

dγ

(y)cosβ

Figure 3.4.

72 3. Existence Techniques I: Methods Based on the Maximum Principle

Let dω be the inﬁnitesimal spatial angle at which the boundary piece dγ

(y)

is seen from x.Wethenhave

dγ

(y)cosβ = |x − y|

d−1

dω (3.4.3)

and cos β =

y−x

|y−x|

. This and (3.4.2) imply

h(x):=



∂

∂ν

Φ(r)dγ

(y)=



dω. (3.4.4)

The geometric meaning of (3.4.4) is that



∂Φ

∂ν

(r)dγ

(y) describes the spa-

tial angle at which the boundary piece γ

is seen at x. Since derivatives of

harmonic functions are harmonic as well, (3.4.4) yields a function h that is

harmonic on Ω

and continuous on ∂Ω

\ (Γ

∩ Γ

). In order to make the

proof of Lemma 3.3.1 geometrically as transparent as possible, from now on,

we only consider the case d = 2 and point out that the proof in the case

d ≥ 3 proceeds analogously.

Figure 3.5.

Let A and B be the two points where Γ

and Γ

intersect (Figure 3.5). Then

h is not continuous at A and B, because

lim

x→A

x∈Γ

h(x)=β, (3.4.5)

lim

x→A

x∈γ

h(x)=β + π, (3.4.6)

lim

x→A

x∈γ

h(x)=α + β. (3.4.7)

Let

ρ(x):=π for x ∈ γ

and

3.4 Boundary Regularity 73

ρ(x):=0 forx ∈ Γ

Then h|

∂Ω

− ρ is continuous on all of ∂Ω

, because

lim

x→A

x∈Γ

(h(x) − ρ(x)) = lim

x→A

x∈Γ

h(x) − 0=β,

lim

x→A

x∈γ

(h(x) − ρ(x)) = lim

x→A

x∈γ

h(x) − π = β + π − π = β.

By assumption, there then exists a function u ∈ C

(Ω

) ∩ C

(

)with

Δu =0 inΩ

u = h|

∂Ω

− ρ on ∂Ω

For

v(x):=

h(x) − u(x)

(3.4.8)

we have

Δv =0 forx ∈ Ω

v(x)=0 forx ∈ Γ

v(x)=1 forx ∈ γ

The strong maximum principle thus implies

v(x) < 1 for all x ∈ Ω

, (3.4.9)

and in particular,

v(x) < 1 for all x ∈ γ

. (3.4.10)

Now

lim

x→A

x∈γ

v(x)=



lim

x→A

x∈γ

h(x) − β



< 1, (3.4.11)

since α<πby assumption. Analogously, lim

x→B

x∈γ

v(x) < 1, and hence since

¯γ

is compact,

v(x) <q<1 for all x ∈ ¯γ

(3.4.12)

for some q>0. We put m := v − w and obtain

m(x)=0 forx ∈ Γ

m(x) ≥ 0forx ∈ γ

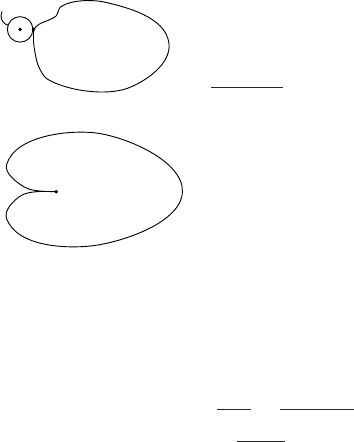
74 3. Existence Techniques I: Methods Based on the Maximum Principle

Since m is continuous in ∂Ω

\ (Γ

∩ Γ

), and ∂Ω

is regular, it follows that

lim

x→x

m(x)=m(x

) for all x

∈ ∂Ω

\ (Γ

∩ Γ

By the maximum principle, m(x) ≥ 0 for all x ∈ Ω

, and since also

lim

x→A

m(x) = lim

x→A

v(x) − w(A) = lim

x→A

v(x) ≥ 0(w is continuous),

we have for all x ∈ ¯γ

w(x) ≤ v(x) <q<1. (3.4.13)

The analogous considerations for M := v + w yield the inequality

−w(x) ≤ v(x) <q<1; (3.4.14)

hence, altogether,

|w(x)| <q<1 for all x ∈ ¯γ



(a)

(b)

B(s, x)

Figure 3.6.

We now wish to present a suﬃcient condition for

the regularity of a boundary point y ∈ ∂Ω:

Deﬁnition 3.4.1: Ω satisﬁes an exterior sphere

condition at y ∈ ∂Ω if there exists x

∈ R

with

B(ρ, x

) ∩

Ω = {y}.

Examples: (a) All convex regions and all re-

gions of class C

satisfy an exterior sphere

condition at every boundary point. (See Fig-

ure 3.6(a).)

(b) At inward cusps, the exterior sphere condi-

tion does not hold. (See Figure 3.6(b).)

Lemma 3.4.1: If Ω satisﬁes an exterior sphere

condition at y, then ∂Ω is regular at y.

Proof:

β(x):=



d−2

−

|x−x

d−2

for d ≥ 3,

|x−x

for d =2,

yields a barrier at y. Namely, β(y) = 0, and β is harmonic in R

\{x

}, hence

in particular in Ω.Sinceforx ∈

Ω \{y}, |x − x

| >,alsoβ(x) > 0 for all

x ∈

Ω \{y}. 

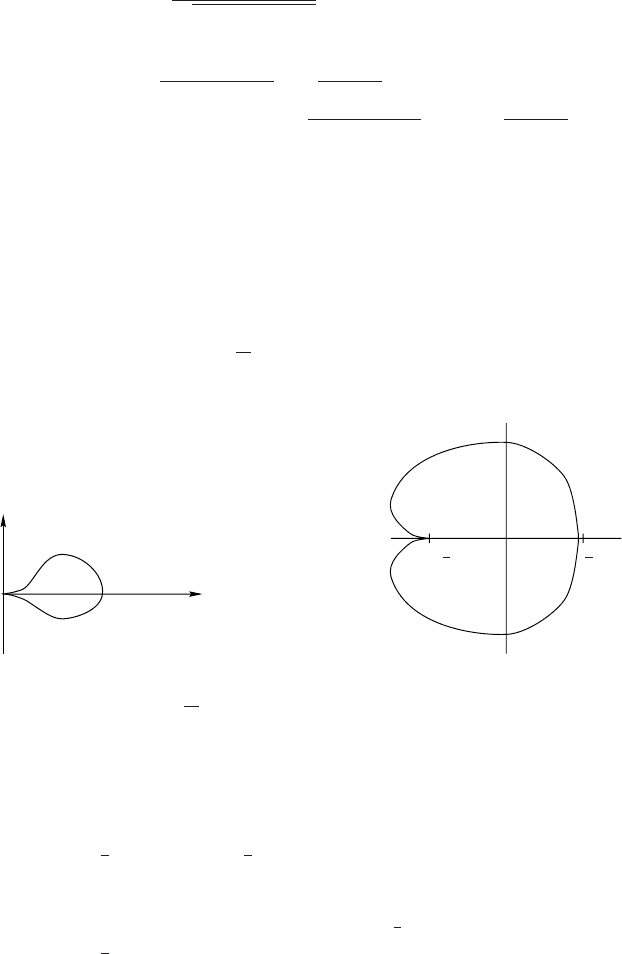
3.4 Boundary Regularity 75

We now wish to present Lebesgue’s example of a nonregular boundary point,

constructing a domain with a suﬃciently pointed inward cusp.

Let R

= {(x, y, z)}, x ∈ [0, 1], ρ

:= y

+ z

u(x, y, z):=





− x)

+ ρ

= v(x, ρ) − 2x ln ρ

with

v(x, ρ)=



(1 − x)

+ ρ

−



+ ρ

+ x ln





1 − x +



(1 − x)

+ ρ



x +



+ ρ





We have

lim

(x,ρ)→0

x>0

v(x, ρ)=1.

The limiting value of −2x ln ρ, however, crucially depends on the sequence

(x, ρ) converging to 0. For example, if ρ = |x|

,wehave

−2x ln ρ = −2nx ln |x|

x→0

−−−→ 0.

On the other hand, if ρ = e

−

, k, x > 0, we have

lim

(x,ρ)→0

(−2x ln ρ)=k>0.

y, z

Figure 3.7.



−

Figure 3.8.

The surface ρ = e

−

has an “inﬁnitely pointed” cusp at 0. (See Figure

3.7.)

Considering u as a potential, this means that the equipotential surfaces of u

for the value 1 + k come together at 0, in such a manner that f



(0) = 0 if the

equipotential surface is given by ρ = f(x). With Ω as an equipotential surface

for 1 + k,thenu solves the exterior Dirichlet problem, and by reﬂection at

the ball (x −

)

+ y

+ z

, one obtains a region Ω



as in Figure 3.8).

Depending on the manner, in which one approaches the cusp, one obtains

diﬀerent limiting values, and this shows that the solution of the potential

problem cannot be continuous at (x, y, z)=



−

, 0, 0



, and hence ∂Ω



is not

regular at



−

, 0, 0



76 3. Existence Techniques I: Methods Based on the Maximum Principle

Summary

The maximum principle is the decisive tool for showing the convergence of

various approximation schemes for harmonic functions. The diﬀerence meth-

ods replace the Laplace equation, a diﬀerential equation, by diﬀerence equa-

tions on a discrete grid, i.e., by ﬁnite-dimensional linear systems. The max-

imum principle implies uniqueness, and since we have a ﬁnite-dimensional

system, then it also implies the existence of a solution, as well as the control

of the solution by its boundary values.

The Perron method constructs a harmonic function with given boundary

values as the supremum of all subharmonic functions with those boundary

values. Whether this solution is continuous at the boundary depends on the

geometry of the boundary, however.

The alternating method of H.A. Schwarz obtains a solution on the union

of two overlapping domains by alternately solving the Dirichlet problem on

each of the two domains with boundary values in the overlapping part coming

from the solution of the previous step on the other domain.

Exercises

3.1 Employing the notation of Section 3.1, let x

∈ Ω

⊂ R

have neighbors

,...,x

.Letx

,...,x

be those points in R

that are neighbors of

exactly two of the points x

,...,x

. We put

:= {x

∈ Ω

: x

,...,x

∈

For u :

→ R, x

∈

, we put

u(x

⎛

⎝



α=1

u(x



β=5

u(x

) − 20u(x

)

⎞

⎠

Discuss the solvability of the Dirichlet problem for the corresponding

Laplace and Poisson equations.

3.2 Let x

∈ Ω

have neighbors x

,...,x

. We consider a diﬀerence operator

Lu for u :

→ R,

Lu(x



α=0

u(x

satisfying the following assumptions:

≥ 0forα =1,...,2d,



α=1

> 0,



α=0

≤ 0.

Prove the weak maximum principle: Lu ≥ 0inΩ

implies

max

u ≤ max