Jost J. Partial Differential Equations
Подождите немного. Документ загружается.

Exercises 77
3.3 Under the assumptions of Section 3.2, assume in addition
b
α
> 0forα =1,...,2d,
and let Ω
h
be discretely connected. Show that if a solution of Lu ≥ 0
assume its maximum at a point of Ω
h
, it has to be constant.
3.4 Carry out the details of the alternating method for the union of three
domains.
3.5 Let u be harmonic on the domain Ω, x
0
∈ Ω,B(x
0
,R) ⊂ Ω, 0 ≤ r ≤ ρ ≤
R, ρ
2
= rR.Then
|ϑ|=1
u(x
0
+ rϑ)u(x
0
+ Rϑ)dϑ =
|ϑ|=1
u
2
(x
0
+ ρϑ)dϑ.
Conclude that if u is constant in some neighborhood of x
0
, it is constant
on all of Ω.
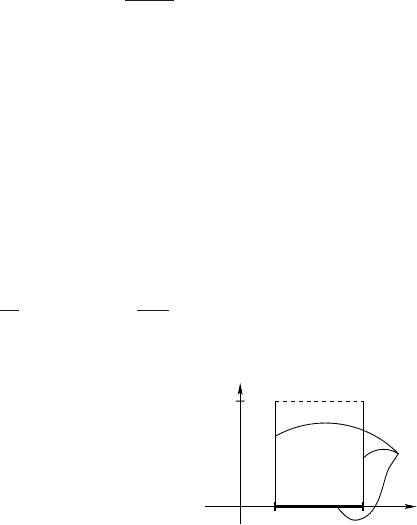
4. Existence Techniques II: Parabolic
Methods. The Heat Equation
4.1 The Heat Equation: Definition and
Maximum Principles
Let Ω ∈ R
d
be open, (0,T) ⊂ R ∪ {∞},
Ω
T
:= Ω × (0,T),
∂
∗
Ω
T
:=
¯
Ω ×{0}
∪
∂Ω × (0,T)
. (See Figure 4.1.)
We call ∂
∗
Ω
T
the reduced boundary of Ω
T
.
For each fixed t ∈ (0,T)letu(x, t) ∈ C
2
(Ω), and for each fixed x ∈ Ω let
u(x, t) ∈ C
1
((0,T)). Moreover, let f ∈ C
0
(∂
∗
Ω
T
), u ∈ C
0
(
¯
Ω
T
). We say that
u solves the heat equation with boundary values f if
u
t
(x, t)=Δ
x
u(x, t) for (x, t) ∈ Ω
T
,
u(x, t)=f (x, t) for (x, t) ∈ ∂
∗
Ω
T
.
(4.1.1)
Written out with a less compressed notation, the differential equation is
∂
∂t
u(x, t)=
d
i=1
∂
2
∂x
2
i
u(x, t).
Ω
T
∂
∗
Ω
T
Ω
x
T
t
Figure 4.1.
Equation (4.1.1) is a linear, parabolic partial
differential equation of second order. The rea-
son that here, in contrast to the Dirichlet prob-
lem for harmonic functions, we are prescribing
boundary values only at the reduced boundary
is that for a solution of a parabolic equation,
the values of u on Ω ×{T } are already deter-
mined by its values on ∂
∗
Ω
T
,asweshallsee
in the sequel.
The heat equation describes the evolution
of temperature in heat-conducting media and is likewise important in many
other diffusion processes. For example, if we have a body in R
3
with given
temperature distribution at time t
0
and if we keep the temperature on its

80 4. Existence Techniques II: Parabolic Methods. The Heat Equation
surface constant, this determines its temperature distribution uniquely at all
times t>t
0
. This is a heuristic reason for prescribing the boundary values
in (4.1.1) only at the reduced boundary.
Replacing t by −t in (4.1.1) does not transform the heat equation into it-
self. Thus, there is a distinction between “past” and “future”. This is likewise
heuristically plausible.
In order to gain some understanding of the heat equation, let us try to
find solutions with separated variables, i.e., of the form
u(x, t)=v(x)w(t). (4.1.2)
Inserting this ansatz into (4.1.1), we obtain
w
t
(t)
w(t)
=
Δv(x)
v(x)
. (4.1.3)
Since the left-hand side of (4.1.3) is a function of t only, while the right-hand
side is a function of x, each of them has to be constant. Thus
Δv(x)=−λv(x), (4.1.4)
w
t
(t)=−λw(t), (4.1.5)
for some constant λ. We consider the case where we assume homogeneous
boundary conditions on ∂Ω ×[0, ∞), i.e.,
u(x, t)=0 forx ∈ ∂Ω,
or equivalently,
v(x)=0 forx ∈ ∂Ω. (4.1.6)
From (4.1.4) we then get through multiplication by v and integration by parts
Ω
|Dv(x)|
2
dx = −
Ω
v(x)Δv(x)dx = λ
Ω
v(x)
2
dx.
Consequently,
λ ≥ 0
(and this is the reason for introducing the minus sign in (4.1.4) and (4.1.5)).
A solution v of (4.1.4), (4.1.6) that is not identically 0 is called an eigen-
function of the Laplace operator, and λ an eigenvalue. We shall see in Sec-
tion 9.5 that the eigenvalues constitute a discrete sequence (λ
n
)
n∈N
, λ
n
→∞
for n →∞. Thus, a nontrivial solution of (4.1.4), (4.1.6) exists precisely if
λ = λ
n
,forsomen ∈ N. The solution of (4.1.5) then is simply given by
w(t)=w(0)e
−λt
.
4.1 The Heat Equation: Definition and Maximum Principles 81
So, if we denote an eigenfunction for the eigenvalue λ
n
by v
n
, we obtain the
solution
u(x, t)=v
n
(x)w(0)e
−λ
n
t
of the heat equation (4.1.1), with the homogeneous boundary condition
u(x, t)=0 forx ∈ ∂Ω
and the initial condition
u(x, 0) = v
n
(x)w(0).
This seems to be a rather special solution. Nevertheless, in a certain sense this
is the prototype of a solution. Namely, because (4.1.1) is a linear equation, any
linear combination of solutions is a solution itself, and so we may take sums
of such solutions for different eigenvalues λ
n
. In fact, as we shall demonstrate
in Section 9.5, any L
2
-function on Ω, and thus in particular any continuous
function f on
¯
Ω, assuming Ω to be bounded, that vanishes on ∂Ω,canbe
expanded as
f(x)=
n∈N
α
n
v
n
(x), (4.1.7)
where the v
n
(x) are the eigenfunctions of Δ, normalized via
Ω
v
n
(x)
2
dx =1
and mutually orthogonal:
Ω
v
n
(x)v
m
(x)dx =0 forn = m.
Then α
n
can be computed as
α
n
=
Ω
v
n
(x)f(x)dx.
We then have an expansion for the solution of
u
t
(x, t)=Δu(x, t)forx ∈ Ω,t ≥ 0,
u(x, t)=0 forx ∈ ∂Ω,t ≥ 0, (4.1.8)
u(x, 0) = f(x)
=
n
α
n
v
n
(x)
, for x ∈ Ω,
namely,

82 4. Existence Techniques II: Parabolic Methods. The Heat Equation
u(x, t)=
n∈N
α
n
e
−λ
n
t
v
n
(x). (4.1.9)
Since all the λ
n
are nonnegative, we see from this representation that all the
“modes” α
n
v
n
(x) of the initial values f are decaying in time for a solution
of the heat equation. In this sense, the heat equation regularizes or smoothes
out its initial values. In particular, since thus all factors e
−λ
n
t
are less than
or equal to 1 for t ≥ 0, the series (4.1.9) converges in L
2
(Ω), because (4.1.7)
does.
If instead of the heat equation we considered the backward heat equation
u
t
= −Δu,
then the analogous expansion would be u(x, t)=
n
α
n
e
λ
n
t
v
n
(x), and so the
modes would grow, and differences would be exponentially enlarged, and in
fact, in general, the series will no longer converge for positive t. This expresses
the distinction between “past” and “future” built into the heat equation and
alluded to above.
If we write
q(x, y, t):=
n∈N
e
−λ
n
t
v
n
(x)v
n
(y), (4.1.10)
and if we can use the results of Section 9.5 to show the convergence of this
series, we may represent the solution u(x, t) of (4.1.8) as
u(x, t)=
n∈N
e
−λ
n
t
v
n
(x)
Ω
v
n
(y)f(y)dy by (4.1.9)
=
Ω
q(x, y, t)f(y)dy.
(4.1.11)
Instead of demonstrating the convergence of the series (4.1.10) and that
u(x, t) given by (4.1.9) is smooth for t>0 and permits differentiation under
the sum, in this chapter we shall pursue a different strategy to construct the
“heat kernel” q(x, y, t)inSection4.3.
For x, y ∈ R
n
, t, t
0
∈ R, t = t
0
, we define the heat kernel at (y,t
0
)as
Λ(x, y, t, t
0
):=
1
(4π |t −t
0
|)
d
2
e
|x−y|
2
4(t
0
−t)
.
We then have
Λ
t
(x, y, t, t
0
)=−
d
2(t − t
0
)
Λ(x, y, t, t
0
)+
|x − y|
2
4(t
0
− t)
2
Λ(x, y, t, t
0
),
Λ
x
i
(x, y, t, t
0
)=
x
i
− y
i
2(t
0
− t)
Λ(x, y, t, t
0
),
Λ
x
i
x
i
(x, y, t, t
0
)=
(x
i
− y
i
)
2
4(t
0
− t)
2
Λ(x, y, t, t
0
)+
1
2(t
0
− t)
Λ(x, y, t, t
0
),

4.1 The Heat Equation: Definition and Maximum Principles 83
i.e.,
Δ
x
Λ(x, y, t, t
0
)=
|x − y|
2
4(t
0
− t)
2
Λ(x, y, t, t
0
)+
d
2(t
0
− t)
Λ(x, y, t, t
0
)
= Λ
t
(x, y, t, t
0
).
The heat kernel thus is a solution of (4.1.1). The heat kernel Λ is similarly
important for the heat equation as the fundamental solution Γ is for the
Laplace equation.
We first wish to derive a representation formula for solutions of the (ho-
mogeneous and inhomogeneous) heat equation that will permit us to compute
the values of u at time T from the values of u and its normal derivative on
∂
∗
Ω
T
. For that purpose, we shall first assume that u solves the equation
u
t
(x, t)=Δu(x, t)+ϕ(x, t)inΩ
T
for some bounded integrable function ϕ(x, t) and that Ω ⊂ R
d
is bounded
and such that the divergence theorem holds. Let v satisfy v
t
= −Δv on Ω
T
.
Then
Ω
T
vϕ dx dt =
Ω
T
v(u
t
− Δu) dx dt
=
Ω
T
0
v(x, t)u
t
(x, t) dt
dx −
T
0
Ω
vΔu dx
dt
=
Ω
v(x, T )u(x, T ) − v(x, 0)u(x, 0) −
T
0
v
t
(x, t)u(x, t)dt
dx
−
T
0
Ω
uΔvdx
dt −
T
0
∂Ω
v
∂u
∂ν
− u
∂v
∂ν
do dt
=
Ω×{T }
vu dx −
Ω×{0}
vu dx −
T
0
∂Ω
v
∂u
∂ν
− u
∂v
∂ν
do dt.
(4.1.12)
For v(x, t):=Λ(x, y, T + ε, t)withT>0andy ∈ Ω
d
fixed we then have,
because of v
t
= −Δv,
Ω×{T }
Λu dx =
Ω
T
Λϕ dx dt +
Ω×{0}
Λu dx
+
T
0
∂Ω
Λ
∂u
∂ν
− u
∂Λ
∂ν
do
dt.
(4.1.13)
For ε → 0, the term on the left-hand side becomes
lim
ε→0
Ω
Λ(x, y, T + ε, T )u(x, T )dx = u(y, T).

84 4. Existence Techniques II: Parabolic Methods. The Heat Equation
Furthermore, Λ(x, y, T + ε, t) is uniformly continuous in ε, x, t for ε ≥ 0,
x ∈ ∂Ω,and0≤ t ≤ T or for x ∈ Ω, t = 0. Thus (4.1.13) implies, letting
ε → 0,
u(y, T )=
Ω
T
Λ(x, y, T, t)ϕ(x, t) dx dt +
Ω
Λ(x, y, T, 0)u(x, 0) dx
+
T
0
∂Ω
Λ(x, y, T, t)
∂u(x, t)
∂ν
− u(x, t)
∂Λ(x, y, T, t)
∂ν
do
dt. (4.1.14)
This formula, however, does not yet solve the initial boundary value problem,
since in (4.1.14), in addition to u(x, t)forx ∈ ∂Ω, t>0, and u(x, 0), also the
normal derivative
∂u
∂ν
(x, t)forx ∈ ∂Ω, t>0, enters. Thus we should try to
replace Λ(x, y, T, t) by a kernel that vanishes on ∂Ω ×(0, ∞). This is the task
that we shall address in Section 4.3. Here, we shall modify the construction
in a somewhat different manner. Namely, we do not replace the kernel, but
change the domain of integration so that the kernel becomes constant on its
boundary. Thus, for μ>0, we let
M(y, T ; μ):=
(x, s) ∈ R
d
× R,s≤ T :
1
(4π(T − s))
d
2
e
−
|x−y|
2
4(T −s)
≥ μ
.
For any y ∈ Ω,T > 0, we may find μ
0
> 0 such that for all μ>μ
0
,
M(y, T ; μ) ⊂ Ω × [0,T].
We always have
(y, T ) ∈ M(y, T; μ),
and in fact, M (y, T; μ) ∩{s = T } consists of the single point (y, T). For t
falling below T, M (y, T; μ) ∩{s = t} is a ball in R
d
with center (y,t)whose
radius first grows but then starts to shrink again if t is decreased further,
until it becomes 0 at a certain value of t.
We then perform the above computation on M(y, T; μ)(μ>μ
0
)inplace
of Ω
T
,with
v(x, t):=Λ(x, y, T + ε, t) − μ,
and as before, we may perform the limit ε 0. Then
v(x, t) = 0 for (x, t) ∈ ∂M(y, T; μ),
so that the corresponding boundary term disappears.
Here, we are interested only in the homogeneous heat equation, and so,
we put ϕ = 0. We then obtain the representation formula
4.1 The Heat Equation: Definition and Maximum Principles 85
u(y, T )=−
∂M(y,T;μ)
u(x, t)
∂Λ
∂ν
x
(x, y, T, t)do(x, t)
= μ
∂M(y,T;μ)
u(x, t)
|x − y|
2(T −t)
do(x, t), (4.1.15)
since
∂Λ
∂ν
x
= −
|x − y|
2(T −t)
Λ = −
|x − y|
2(T −t)
μ on ∂M(y,T; μ).
In general, the maximum principles for parabolic equations are quali-
tatively different from those for elliptic equations. Namely, one often gets
stronger conclusions in the parabolic case.
Theorem 4.1.1: Let u be as in the assumptions of (4.1.1). Let Ω ⊂ R
d
be
open and bounded and
Δu − u
t
≥ 0 in Ω
T
. (4.1.16)
We then have
sup
¯
Ω
T
u =sup
∂
∗
Ω
T
u. (4.1.17)
(If T<∞, we can take max in place of sup.)
Proof: Without loss of generality T<∞.
(i) Suppose first
Δu − u
t
> 0inΩ
T
. (4.1.18)
For 0 <ε<T,bycontinuityofu and compactness of
¯
Ω
T −ε
,there
exists (x
0
,t
0
) ∈
¯
Ω
T −ε
with
u(x
0
,t
0
)=max
¯
Ω
T −ε
u. (4.1.19)
If we had (x
0
,t
0
) ∈ Ω
T −ε
,thenΔu(x
0
,t
0
) ≤ 0, ∇u(x
0
,t
0
)=0,
u
t
(x
0
,t
0
) = 0 would lead to a contradiction; hence we must have
(x
0
,t
0
) ∈ ∂Ω
T −ε
.Fort = T −ε and x ∈ Ω, we would get Δu(x
0
,t
0
) ≤ 0,
u
t
(x
0
,t
0
) ≥ 0, likewise contradicting (4.1.18). Thus we conclude that
max
¯
Ω
T −ε
u =max
∂
∗
Ω
T −ε
u, (4.1.20)
and for ε → 0, (4.1.20) yields the claim, since u is continuous.

86 4. Existence Techniques II: Parabolic Methods. The Heat Equation
(ii) If we have more generally Δu − u
t
≥ 0, we let v := u − εt, ε>0. We
have
v
t
= u
t
− ε ≤ Δu − ε = Δv − ε<Δv,
and thus by (i),
max
¯
Ω
T
u =max
¯
Ω
T
(v + εt) ≤ max
¯
Ω
T
v + εT =max
∂
∗
Ω
T
v + εT ≤ max
∂
∗
Ω
T
u + εT,
and ε → 0 yields the claim.
Theorem 4.1.1 directly leads to a uniqueness result:
Corollary 4.1.1: Let u, v be solutions of (4.1.1) with u = v on ∂
∗
Ω
T
, where
Ω ⊂ R
d
is bounded. Then u = v on
¯
Ω
T
.
Proof: We apply Theorem 4.1.1 to u − v and v − u.
This uniqueness holds only for bounded Ω, however. If, e.g., Ω = R
d
, unique-
ness holds only under additional assumptions on the solution u.
Theorem 4.1.2: Let Ω = R
d
and suppose
Δu − u
t
≥ 0 in Ω
T
,
u(x, t) ≤ Me
λ|x|
2
in Ω
T
for M,λ > 0, (4.1.21)
u(x, 0) = f(x) x ∈ Ω = R
d
.
Then
sup
¯
Ω
T
u ≤ sup
R
d
f. (4.1.22)
Remark: This maximum principle implies the uniqueness of solutions of the
differential equation
Δu = u
t
on Ω
T
= R
d
× (0,T),
u(x, 0) = f(x)forx ∈ R
d
,
u(x, t) ≤ Me
λ|x|
2
for (x, t) ∈ Ω
T
.
The condition (4.1.21) is a condition for the growth of u at infinity. If this
condtion does not hold, there are counterexamples for uniqueness. For exam-
ple, let us choose
u(x, t):=
∞
n=0
g
n
(t)
(2n)!
x
2n
