Jost J. Partial Differential Equations
Подождите немного. Документ загружается.

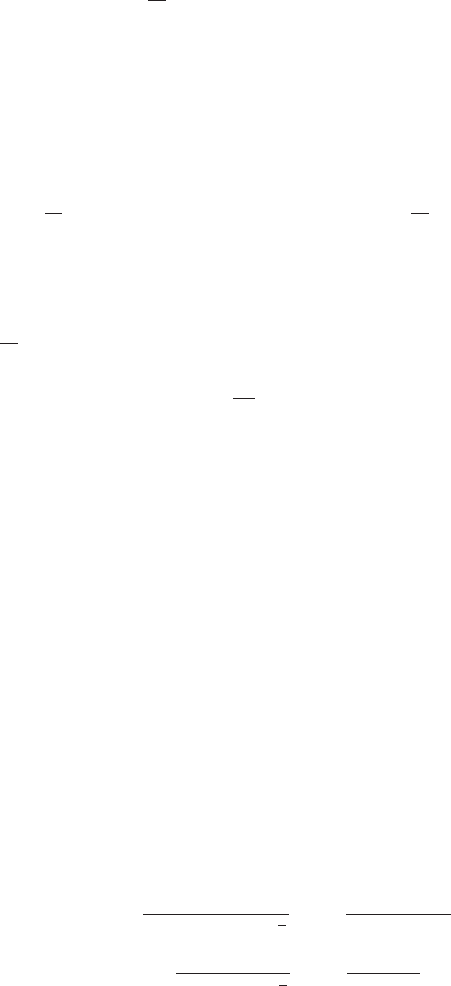
4.1 The Heat Equation: Definition and Maximum Principles 87
with
g(t):=
e
−1
t
k
t>0, for some k>1,
0 t =0,
v(x, t):=0 forall(x, t) ∈ R × (0, ∞).
Then u and v are solutions of (4.1.1) with f(x) = 0. For further details we
refer to the book of F. John [10].
Proof of Theorem 4.1.2: Since we can divide the interval (0,T) into subinter-
vals of length τ<
1
4λ
, it suffices to prove the claim for T<
1
4λ
, because we
shall then get
sup
R
d
×[0,kτ ]
u ≤ sup
R
d
×[0,(k−1)τ ]
u ≤···≤sup
R
d
f(x).
Thus let T<
1
4λ
. We may then find ε>0with
T + ε<
1
4λ
. (4.1.23)
For fixed y ∈ R
d
and δ>0, we consider
(x, t):=u(x, t) − δΛ(x, y, t, T + ε), 0 ≤ t ≤ T. (4.1.24)
It follows that
v
δ
t
− Δv
δ
= u
t
− Δu ≤ 0, (4.1.25)
since Λ is a solution of the heat equation. For Ω
ρ
:= B(y, ρ), we thus obtain
from Theorem 4.1.1
v
δ
(y, t) ≤ max
∂
∗
Ω
ρ
v
δ
. (4.1.26)
Moreover,
v
δ
(x, 0) ≤ u(x, 0) ≤ sup
R
d
f, (4.1.27)
and for |x − y| = ρ,
v
δ
(x, t) ≤ Me
λ|x|
2
− δ
1
(4π(T + ε − t))
d
2
exp
ρ
2
4(T + ε − t)
≤ Me
λ(|y|+ρ)
2
− δ
1
(4π(T + ε))
d
2
exp
ρ
2
4(T + ε)
.
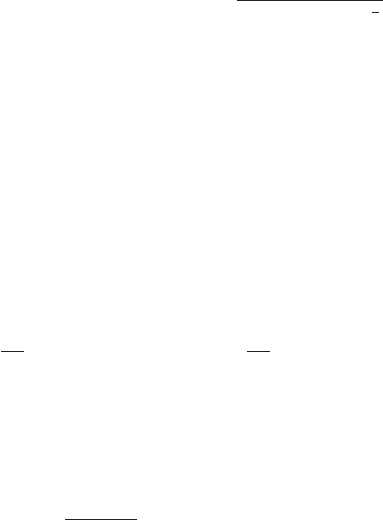
88 4. Existence Techniques II: Parabolic Methods. The Heat Equation
Because of (4.1.23), for sufficiently large ρ, the second term has a larger
exponent than the first, and so the whole expression can be made arbitrarily
negative; in particular, we can achieve that it is not larger than sup
R
d
f.
Consequently,
v
δ
≤ sup
R
d
f on ∂
∗
Ω
ρ
. (4.1.28)
Thus, (4.1.26) and (4.1.28) yield
v
δ
(y, t)=u(y,t) − δΛ(y,y, t, T + ε)=u(y,t) −δ
1
(4π(T + ε − t))
d
2
≤ sup
R
d
f.
The conclusion follows by letting δ → 0.
Actually, we can use the representation formula (4.1.12) to obtain a strong
maximum principle for the heat equation, in the same manner as the mean
value formula could be used to obtain Corollary 1.2.3:
Theorem 4.1.3: Let Ω ⊂ R
d
be open and bounded and
Δu − u
t
=0 in Ω
T
,
with the regularity properties specified at the beginning of this section. Then
if there exists some (x
0
,t
0
) ∈ Ω × (0,T] with
u(x
0
,t
0
)=max
Ω
T
u (or with u(x
0
,t
0
)=min
Ω
T
u),
then u is constant in
¯
Ω
t
0
.
Proof: The proof is the same as that of Lemma 1.2.1, using the representation
formula (4.1.12). (Note that by applying (4.1.12) to the function u ≡ 1, we
obtain
μ
∂M(y,T;μ)
|x − y|
2(T −t)
do(x, t)=1,
and so a general u that solves the heat equation is indeed represented as some
average. Also, M (y,T; μ
2
) ⊂ M(y, T; μ
1
)forμ
1
≤ μ
2
,andasμ →∞,the
sets M(y, T; μ) shrink to the point (y,T).)
Of course, the maximum principle also holds for subsolutions, i.e., if
Δu − u
t
≥ 0inΩ
T
.
In that case, we get the inequality “≤” in place of “=” in (4.1.12), which
is what is required for the proof of the maximum principle. Likewise, the
statement with the minimum holds for solutions of
Δu − u
t
≤ 0.
Slightly more generally, we even have

4.1 The Heat Equation: Definition and Maximum Principles 89
Corollary 4.1.2: Let Ω ⊂ R
d
be open and bounded and
Δu(x, t)+c(x, t)u(x, t) − u
t
(x, t) ≥ 0 in Ω
T
,
with some bounded function
c(x, t) ≤ 0 in Ω
T
. (4.1.29)
Then if there exists some (x
0
,t
0
) ∈ Ω × (0,T] with
u(x
0
,t
0
)=max
Ω
T
u ≥ 0, (4.1.30)
then u is constant in
¯
Ω
t
0
.
Proof: Our scheme of proof still applies because, since c is nonpositive, at
a nonnegative maximum point (x
0
,t
0
)ofu, c(x
0
,t
0
)u(x
0
,t
0
) ≤ 0which
strengthens the inequality used in the proof.
Again, we obtain a minimum principle when we reverse all signs.
For use in §5.1 below, we now derive a parabolic version of E.Hopf’s boundary
point lemma 2.1.2. Compared with §2.1, we shall reverse here the scheme of
proof, that is, deduce the boundary point lemma from the strong maximum
principle instead of the other way around. This is possible because here we
consider less general differential operators than the ones in §2.1sothatwe
could deduce our maximum principle from the representation formula. Of
course, one can also deduce general Hopf type maximum principles in the
parabolic case, in a manner analogous to §2.1, but we do not pursue that
here as it will not yield conceptually or technically new insights.
Lemma 4.1.1: Suppose the function c is bounded and satisfies c(x, t) ≤ 0 in
Ω
T
.Letu solve the differential inequality
Δu(x, t)+c(x, t)u(x, t) − u
t
(x, t) ≥ 0 in Ω
T
,
and let (x
0
,t
0
) ∈ ∂
∗
Ω
T
. Moreover, assume
(i) u is continuous at (x
0
,t
0
);
(ii) u(x
0
,t
0
) ≥ 0 if c(x) ≡ 0;
(iii) u(x
0
,t
0
) >u(x, t) for all (x, t) ∈ Ω
T
;
(iv) there exists a ball
˚
B((y, t
1
),R) ⊂ Ω
T
with (x
0
,t
0
) ∈ ∂B((y, t
1
),R).
We then have, with r := |(x, t) − (y, t
1
)|,
∂u
∂r
(x
0
,t
0
) > 0, (4.1.31)
provided that this derivative (in the direction of the exterior normal of Ω
T
)
exists.
90 4. Existence Techniques II: Parabolic Methods. The Heat Equation
Proof: With the auxiliary function
v(x):=e
−γ(|x−y|
2
+(t−t
1
)
2
)
− e
−γR
2
,
the proof proceeds as the one of Lemma 2.1.2, employing this time the max-
imum principle Theorem 4.1.3.
I do not know of any good recent book that gives a detailed and systematic
presentation of parabolic differential equations. Some older, but still useful,
references are [6], [16].

4.2 The Fundamental Solution of the Heat Equation 91
4.2 The Fundamental Solution of the Heat Equation.
The Heat Equation and the Laplace Equation
We first consider the so-called fundamental solution
K(x, y, t)=Λ(x, y, t, 0) =
1
(4πt)
d
2
e
−
|x−y|
2
4t
, (4.2.1)
and we first observe that for all x ∈ R
d
, t>0,
R
d
K(x, y, t)dy =
1
(4πt)
d
2
dω
d
∞
0
e
−
r
2
4t
r
d−1
dr =
1
π
d
2
dω
d
∞
0
e
−s
2
s
d−1
ds
=
1
π
d
2
R
d
e
−|y|
2
dy =1. (4.2.2)
For bounded and continuous f : R
d
→ R, we consider the convolution
u(x, t)=
R
d
K(x, y, t)f(y)dy =
1
(4πt)
d
2
R
d
e
−
|x−y|
2
4t
f(y)dy. (4.2.3)
Lemma 4.2.1: Let f : R
d
→ R be bounded and continuous. Then
u(x, t)=
R
d
K(x, y, t)f(y)dy
is of class C
∞
on R
d
× (0, ∞), and it solves the heat equation
u
t
= Δu. (4.2.4)
Proof: That u is of class C
∞
follows, by differentiating under the inte-
gral (which is permitted by standard theorems), from the C
∞
property of
K(x, y, t). Consequently, we also obtain
∂
∂t
u(x, t)=
R
d
∂
∂t
K(x, y, t)f(y)dy =
R
d
Δ
x
K(x, y, t)f(y)dy = Δ
x
u(x, t).
Lemma 4.2.2: Under the assumptions of Lemma 4.2.1, we have for every
x ∈ R
d
,
lim
t→0
u(x, t)=f (x).

92 4. Existence Techniques II: Parabolic Methods. The Heat Equation
Proof:
|f(x) − u(x, t)| =
f(x) −
R
d
K(x, y, t)f(y)dy
=
R
d
K(x, y, t)(f(x) − f(y))dy
with (4.2.2)
=
1
(4πt)
d
2
∞
0
e
−
r
2
4t
r
d−1
S
d−1
(f(x) − f(x + rξ)) do(ξ) dr
=
1
π
d
2
∞
0
e
−s
2
s
d−1
S
d−1
f(x) − f(x +2
√
tsξ)
do(ξ) ds
=
···
M
0
···+ ···
∞
M
···
≤ sup
y∈B(x,2
√
tM)
|f(x) − f(y)| +2sup
R
d
|f|
dω
d
π
d
2
∞
M
e
−s
2
s
d−1
ds.
Given ε>0, we first choose M so large that the second summand is less
than ε/2, and we then choose t
0
> 0sosmallthatforallt with 0 <t<t
0
,
the first summand is less than ε/2 as well. This implies the continuity.
By (4.2.3), we have thus found a solution of the initial value problem
u
t
(x, t) − Δu(x, t)=0 forx ∈ R
d
,t>0,
u(x, 0) = f(x),
for the heat equation. By Theorem 4.1.2 this is the only solution that grows
at most exponentially.
According to the physical interpretation, u(x, t) is supposed to describe
the evolution in time of the temperature for initial values f(x). We should
note, however, that in contrast to physically more realistic theories, we here
obtain an infinite propagation speed as for any positive time t>0, the
temperature u(x, t)atthepointx is influenced by the initial values at all
arbitrarily far away points y, although the strength decays exponentially with
the distance |x − y|.
In the case where f has compact support K, i.e., f(x)=0forx/∈ K,the
function from (4.2.3) satisfies
|u(x, t)|≤
1
(4πt)
d
2
e
−
dist(x,K)
2
4t
K
|f(y)|dy, (4.2.5)
whichgoesto0ast →∞.
Remark: (4.2.5) yields an explicit exponential rate of convergence!
More generally, one is interested in the initial boundary value problem for
the inhomogeneous heat equation:

4.2 The Fundamental Solution of the Heat Equation 93
Let Ω ⊂ R
d
be a domain, and let ϕ ∈ C
0
(Ω × [0, ∞)), f ∈ C
0
(Ω), g ∈
C
0
(∂Ω × (0, ∞)) be given. We wish to find a solution of
∂u(x, t)
∂t
− Δu(x, t)=ϕ(x, t)inΩ ×(0, ∞),
u(x, 0) = f(x)inΩ, (4.2.6)
u(x, t)=g(x, t)forx ∈ ∂Ω, t ∈ (0, ∞).
In order for this problem to make sense, one should require a compatibility
condition between the initial and the boundary values: f ∈ C
0
(
¯
Ω), g ∈
C
0
(∂Ω × [0, ∞)), and
f(x)=g(x, 0) for x ∈ ∂Ω. (4.2.7)
We want to investigate the connection between this problem and the Dirichlet
problem for the Laplace equation, and for that purpose, we consider the
case where ϕ ≡ 0andg(x, t)=g(x) is independent of t. For the following
consideration whose purpose is to serve as motivation, we assume that u(x, t)
is differentiable sufficiently many times up to the boundary. (Of course, this
is an issue that will need a more careful study later on.) We then compute
∂
∂t
− Δ
1
2
u
2
t
= u
t
u
tt
− u
t
Δu
t
−
d
i=1
u
2
x
i
t
= u
t
∂
∂t
(u
t
− Δu) −
d
i=1
u
2
x
i
t
= −
d
i=1
u
2
x
i
t
≤ 0. (4.2.8)
According to Theorem 4.1.1,
v(t):=sup
x∈Ω
∂u(x, t)
∂t
2
then is a nonincreasing function of t.
We now consider
E(u(·,t)) =
1
2
Ω
d
i=1
u
2
x
i
dx
and compute
∂
∂t
E(u(·,t)) =
Ω
d
i=1
u
tx
i
u
x
i
dx
= −
Ω
u
t
Δudx, since u
t
(x, t)=
∂
∂t
g(x)=0 forx ∈ ∂Ω
= −
Ω
u
2
t
dx ≤ 0. (4.2.9)

94 4. Existence Techniques II: Parabolic Methods. The Heat Equation
With (4.2.8), we then conclude that
∂
2
∂t
2
E(u(·,t)) = −
Ω
∂
∂t
u
2
t
dx = −
Ω
Δu
2
t
dx +2
Ω
d
i=1
u
2
x
i
t
dx
= −
∂Ω
∂
∂ν
u
2
t
do(x)+2
Ω
d
i=1
u
2
x
i
t
dx.
Since u
2
t
≥ 0inΩ, u
2
t
=0on∂Ω,wehaveon∂Ω,
∂
∂ν
u
2
t
≤ 0.
It follows that
∂
2
∂t
2
E(u(·,t)) ≥ 0. (4.2.10)
Thus E(u(·,t)) is a monotonically nonincreasing and convex function of t.In
particular, we obtain
∂
∂t
E(u(·,t)) ≤ α := lim
t→∞
∂
∂t
E(u(·,t)) ≤ 0. (4.2.11)
Since E(u(·,t)) ≥ 0 for all t,wemusthaveα = 0, because otherwise for
sufficiently large T ,
E(u(·,T)) = E(u(·, 0)) +
T
0
∂
∂t
E(u(·,t))dt ≤ E(u(·, 0)) + αT < 0.
Thus it follows that
lim
t→∞
Ω
u
2
t
dx =0. (4.2.12)
In order to get pointwise convergence as well, we have to utilize the maximum
principle once more. We extend u
2
t
(x, 0) from Ω to all of R
d
as a nonnegative,
continuous function l with compact support and put
v(x, t):=
R
d
1
(4πt)
d
2
e
−
|x−y|
2
4t
l(y)dy. (4.2.13)
We then have
v
t
− Δv =0,
and since l ≥ 0, also
v ≥ 0,

4.2 The Fundamental Solution of the Heat Equation 95
and thus in particular
v ≥ u
2
t
on ∂Ω.
Thus w := u
2
t
− v satisfies
∂
∂t
w − Δw ≤ 0inΩ, (4.2.14)
w ≤ 0on∂Ω,
w(x, 0) = 0 for x ∈ Ω,t =0.
Theorem 4.1.1 then implies
w(x, t) ≤ 0,
i.e.,
u
2
t
(x, t) ≤ v(x, t) for all x ∈ Ω,t > 0. (4.2.15)
Since l has compact support, from Lemma 4.2.2
lim
t→∞
v(x, t) = 0 for all x ∈ Ω,
and thus also
lim
t→∞
u
2
t
(x, t) = 0 for all x ∈ Ω. (4.2.16)
We thus conclude that provided that our regularity assumptions are valid
the time derivative of a solution of our initial boundary value theorem with
boundary values that are constant in time goes to 0 as t →∞.Thus,ifwe
can show that u(x, t) converges for t →∞with respect to x in C
2
, the limit
function u
∞
needs to satisfy
Δu
∞
=0,
i.e., be harmonic. If we can even show convergence up to the boundary, then
u
∞
satisfies the Dirichlet condition
u
∞
(x)=g(x)forx ∈ ∂Ω.
From the remark about (4.2.5), we even see that u
t
(x, t) converges to 0 ex-
ponentially in t.
If we know already that the Dirichlet problem
Δu
∞
=0 inΩ,
u
∞
= g on ∂Ω, (4.2.17)
admits a solution, it is easy to show that any solution u(x, t) of the heat
equation with appropriate boundary values converges to u
∞
. Namely, we
even have the following result:

96 4. Existence Techniques II: Parabolic Methods. The Heat Equation
Theorem 4.2.1: Let Ω be a bounded domain in R
d
,andletg(x, t) be con-
tinuous on ∂Ω ×(0, ∞), and suppose
lim
t→∞
g(x, t)=g(x) uniformly in x ∈ ∂Ω. (4.2.18)
Let F (x, t) be continuous on Ω × (0, ∞), and suppose
lim
t→∞
F (x, t)=F (x) uniformly in x ∈ Ω. (4.2.19)
Let u(x, t) be a solution of
Δu(x, t) −
∂
∂t
u(x, t)=F (x, t) for x ∈ Ω, 0 <t<∞,
u(x, t)=g(x, t) for x ∈ ∂Ω, 0 <t<∞. (4.2.20)
Let v(x) be a solution of
Δv(x)=F (x) for x ∈ Ω,
v(x)=g(x) for x ∈ ∂Ω. (4.2.21)
We then have
lim
t→∞
u(x, t)=v(x) uniformly in x ∈ Ω. (4.2.22)
Proof: We consider the difference
w(x, t)=u(x, t) − v(x). (4.2.23)
Then
Δw(x, t) −
∂
∂t
w(x, t)=F (x, t) − F (x)inΩ × (0, ∞),
w(x, t)=g(x, t) − g(x)in∂Ω × (0, ∞), (4.2.24)
and the claim follows from the following lemma:
Lemma 4.2.3: Let Ω be a bounded domain in R
d
,letφ(x, t) be continuous
on Ω ×(0, ∞), and suppose
lim
t→∞
φ(x, t)=0 uniformly in x ∈ Ω. (4.2.25)
Let γ(x, t) be continuous on ∂Ω × (0, ∞), and suppose
lim
t→∞
γ(x, t)=0 uniformly in x ∈ ∂Ω. (4.2.26)
Let w(x, t) be a solution of
