Jost J. Partial Differential Equations

Подождите немного. Документ загружается.

3.1 Diﬀerence Methods: Discretization of Diﬀerential Equations 57

Proof: As already observed, the discrete problem constitutes a ﬁnite system

of linear equations with the same number of equations and unknowns. Since

by Corollary 3.1.1, for homogeneous boundary data g

= 0, the homogeneous

solution u

= 0 is the unique solution, the fundamental theorem of linear

algebra implies the existence of a solution for an arbitrary right-hand side,

i.e., for arbitrary g

. 

The solution of the discrete Poisson equation

= f

in Ω

(3.1.17)

with given f

is similarly simple; here, without loss of generality, we consider

only the homogeneous boundary condition

=0 onΓ

, (3.1.18)

because an inhomogeneous condition can be treated by adding a solution of

the corresponding discrete Laplace equation.

In order to represent the solution, we shall now construct a Green function

(x, y). For that purpose, we consider a particular f

in (3.1.17), namely,

(x)=



0forx = y,

for x = y,

for given y ∈ Ω

.ThenG

(x, y) is deﬁned as the solution of (3.1.17), (3.1.18)

for that f

. The solution for an arbitrary f

is then obtained as

(x)=h



y∈Ω

(x, y)f

(y). (3.1.19)

In order to show that solutions of the discrete Laplace equation Δ

in Ω

for h → 0 converge to a solution of the Laplace equation Δu =0inΩ

we need estimates for the u

that do not depend on h. It turns out that as

in the continuous case, such estimates can be obtained with the help of the

maximum principle. Namely, for the symmetric diﬀerence quotient

˜ı

(x):=



u(x

,...,x

i−1

+ h, x

i+1

,...,x

)

− u(x

,...,x

i−1

− h, x

i+1

,...,x

)



(x)+u

¯ı

(x)) (3.1.20)

we may prove in complete analogy with Corollary 1.2.7 the following result:

Lemma 3.1.1: Suppose that in Ω

(x)=f

(x). (3.1.21)

58 3. Existence Techniques I: Methods Based on the Maximum Principle

Let x

∈ Ω

, and suppose that x

and all its neighbors have distance greater

than or equal to R from Γ

. Then



˜ı

)



≤

max



max



. (3.1.22)

Proof: Without loss of generality i =1,x

= 0. We put

μ := max



,M:= max



We consider once more the auxiliary function

(x):=

|x|

+ x

(R − x

)



dμ



Because of

|x|



i=1



+ h)

+(x

− h)

− 2(x

)



=2d,

we have again

(x)=−M

as well as

(0,x

,...,x

) ≥ 0 for all x

,...,x

(x) ≥ μ for |x|≥R, 0 ≤ x

≤ R.

Furthermore, for ¯u

(x):=

,...,x

) − u

(−x

,...,x

)),



¯u

(x)



≤ M for those x ∈ Ω

, for which this expression is

deﬁned,

¯u

(0,x

,...,x

) = 0 for all x

,...,x



¯u

(x)



≤ μ for |x|≥R, x

≥ 0.

On the discretization B

of the half-ball B

:= {|x|≤R, x

> 0},wethus

have



± ¯u



≤ 0

as well as

± ¯u

≥ 0 on the discrete boundary of B

(in order to be precise, here one should take as the discrete boundary all

vertices in the exterior of

that have at least one neighbor in

). The

maximum principle (Theorem 3.1.1) yields

3.1 Diﬀerence Methods: Discretization of Diﬀerential Equations 59



¯u



≤ v

in B

and hence



˜ı

(0)



¯u

(h, 0,...,0)



≤

(h, 0,...,0)

dμ

M +

(1 − d)h.



For solutions of the discrete Laplace equation

=0 inΩ

, (3.1.23)

we then inductively get estimates for higher-order diﬀerence quotients, be-

cause if u

is a solution, so are all diﬀerence quotients u

¯ı

˜ı

i¯ı

˜ı¯ı

, etc.

For example, from (3.1.22) we obtain for a solution of (3.1.23) that if x

far enough from the boundary Γ

,then



˜ı˜ı

)



≤

max



˜ı



≤

max



max



. (3.1.24)

Thus, by induction, we can bound diﬀerence quotients of any order, and we

obtain the following theorem:

Theorem 3.1.2: If all solutions u

=0 in Ω

are bounded independently of h (i.e., max



≤ μ), then in any subdomain

Ω ⊂⊂ Ω, some subsequence of u

converges to a harmonic function as h → 0.

Convergence here ﬁrst means convergence with respect to the supremum

norm, i.e.,

lim

n→0

max

x∈Ω

(x) − u(x)| =0,

with harmonic u. By the preceding considerations, however, the diﬀerence

quotients of u

converge to the corresponding derivatives of u as well. 

We wish to brieﬂy discuss some aspects of diﬀerence equations that are

important in numerical analysis. There, for theoretical reasons, one assumes

that one already knows the existence of a smooth solution of the diﬀerential

equation under consideration, and one wants to approximate that solution

by solutions of diﬀerence equations. For that purpose, let L be an elliptic

diﬀerential operator and consider discrete operators L

that are applied to

the restriction of a function u to the lattice Ω

60 3. Existence Techniques I: Methods Based on the Maximum Principle

Deﬁnition 3.1.1: The diﬀerence scheme L

is called consistent with L if

lim

h→0

(Lu − L

u)=0

for all u ∈ C

(

Ω).

The scheme L

is called convergent to L if the solutions u, u

Lu = f in Ω,u = ϕ on ∂Ω,

= f

in Ω

, where f

is the restriction of f to Ω

= ϕ

on Γ

, where ϕ

is the restriction to Ω

of a

continuous extension of ϕ,

satisfy

lim

h→0

max

x∈Ω

(x) − u(x)| =0.

In order to see the relation between convergence and consistency we con-

sider the “global error”

σ(x):=u

(x) − u(x)

and the “local error”

s(x):=L

u(x) − Lu(x)

and compute, for x ∈ Ω

σ(x)=L

(x) − L

u(x)=f

(x) − Lu(x) − s(x)

= −s(x), since f

(x)=f(x)=Lu(x).

Since

lim

h→0

sup

x∈Γ

|σ(x)| =0,

the problem essentially is

σ(x)=−s(x)inΩ

σ(x)=0 onΓ

In order to deduce the convergence of the scheme from its consistency, one

thus needs to show that if s(x) tends to 0, so does the solution σ(x), and

in fact uniformly. Thus, the inverses L

−1

have to remain bounded in a sense

that we shall not make precise here. This property is called stability.

In the spirit of these notions, let us show the following simple convergence

result:

3.1 Diﬀerence Methods: Discretization of Diﬀerential Equations 61

Theorem 3.1.3: Let u ∈ C

(

Ω) be a solution of

Δu = f in Ω,

u = ϕ on ∂Ω.

Let u

be the solution

= f

in Ω

= ϕ

on Γ

where f

,ϕ

are deﬁned as above. Then

max

x∈Ω



(x) − u(x)



→ 0 for h → 0.

Proof: Taylor’s formula implies that the second-order diﬀerence quotients

(which depend on the mesh size h) satisfy

i¯ı

(x)=

∂

(∂x

)



,...,x

i−1

+ δ

i+1

,...,x



with −h ≤ δ

≤ h.Sinceu ∈ C

(

Ω), we have

sup

|δ

|≤h



∂

(∂x

)

,...,x

+ δ

,...,x

) −

∂

(∂x

)

,...,x

)



→ 0

for h → 0, and thus the above local error satisﬁes

sup |s(x)|→0forh → 0.

Now let Ω becontainedinaballB(x

,R); without loss of generality

=0.

The maximum principle then implies, through comparison with the func-

tion R

−|x|

, that a solution v of

v = η in Ω

v =0 onΓ

satisﬁes the estimate

|v(x)|≤

sup |η|



−|x|



Thus, the global error satisﬁes

sup |σ(x)|≤

sup |s(x)|,

hence the desired convergence. 

62 3. Existence Techniques I: Methods Based on the Maximum Principle

3.2 The Perron Method

Let us ﬁrst recall the notion of a subharmonic function from Section 1.2, since

this will play a crucial role:

Deﬁnition 3.2.1: Let Ω ⊂ R

, f : Ω → [−∞, ∞) upper semicontinuous in

Ω, f ≡−∞. The function f is called subharmonic in Ω if for all Ω



⊂⊂ Ω,

the following property holds:

If u is harmonic in Ω



,andf ≤ u on ∂Ω



, then also

f ≤ u in Ω



The next lemma likewise follows from the results of Section 1.2:

Lemma 3.2.1:

(i) Strong maximum principle: Let v be subharmonic in Ω. If there exists

∈ Ω with v(x

)=sup

v(x), then v is constant. In particular, if

v ∈ C

(

Ω), then v(x) ≤ max

∂Ω

v(y) for all x ∈ R.

(ii) If v

,...,v

are subharmonic, so is v := max(v

,...,v

(iii) If v ∈ C

(

Ω) is subharmonic and B(y,R) ⊂⊂ Ω, then the harmonic

replacement ¯v of v, deﬁned by

¯v(x):=



v(x) for x ∈ Ω \ B(y, R),

−|x−y|



∂B(y,R)

v(z)

|z−x|

do(z) for x ∈ B(y, R),

is subharmonic in Ω (and harmonic in B(y,R)).

Proof:

(i) This is the strong maximum principle for subharmonic functions. Al-

though we have not written it down explicitly, it is a direct consequence

of Theorem 1.2.2 and Lemma 1.2.1.

(ii) Let Ω



⊂⊂ Ω, u harmonic on ∂Ω



, v ≤ u on ∂Ω



.Thenalso

≤ u on ∂Ω



for i =1,...,n,

and hence, since v

is subharmonic,

≤ u on Ω



This implies

≤ u on Ω



showing that v is subharmonic.

3.2 The Perron Method 63

(iii) First v ≤ ¯v,sincev is subharmonic. Let Ω



⊂⊂ Ω, u harmonic on Ω



v ≤ u on ∂Ω



.Sincev ≤ v,alsov ≤ u on ∂Ω



, and thus, since v is

subharmonic, v ≤ u on Ω



and thus v ≤ u on Ω



B(y, R). Therefore,

also

v ≤ u on Ω



∩ ∂B(y, R). Since v is harmonic, hence subharmonic

on Ω



∩ B(y, R), we get v ≤ u on Ω



∩ B(y, R). Altogether, we obtain

v ≤ u on Ω



. This shows that v is subharmonic.



For the sequel, let ϕ be a bounded function on Ω (not necessarily contin-

uous).

Deﬁnition 3.2.2: A subharmonic function u ∈ C

(

Ω) is called a subfunc-

tion with respect to ϕ if

u ≤ ϕ for all x ∈ ∂Ω.

Let S

be the set of all subfunctions with respect to ϕ. (Analogously, a su-

perharmonic function u ∈ C

(

Ω) is called superfunction with respect to ϕ if

u ≥ ϕ on ∂Ω.)

The key point of the Perron method is contained in the following theorem:

Theorem 3.2.1: Let

u(x):= sup

v∈S

v(x). (3.2.1)

Then u is harmonic.

Remark: If w ∈ C

(Ω) ∩ C

(

Ω)isharmoniconΩ,andifw = ϕ on ∂Ω,the

maximum principle implies that for all subfunctions v ∈ S

,wehavev ≤ w

in Ω and hence

w(x)= sup

v∈S

v(x).

Thus, w satisﬁes an extremal property. The idea of the Perron method (and

the content of Theorem 3.2.1) is that, conversely, each supremum in S

yields

a harmonic function.

Proof of Theorem 3.2.1: First of all, u is well-deﬁned, since by the maximum

principle v ≤ sup

∂Ω

ϕ<∞ for all v ∈ S

.Nowlety ∈ Ω be arbitrary.

By (3.2.1) there exists a sequence {v

}⊂S

with lim

n→∞

(y)=u(y).

Replacing v

by max(v

,...,v

, inf

∂Ω

ϕ), we may assume without loss of

generality that (v

)

n∈N

is a monotonically increasing, bounded sequence. We

now choose R with B(y, R) ⊂⊂ Ω and consider the harmonic replacements

¯v

for B(y,R). The maximum principle implies that (¯v

)

n∈N

likewise is a

monotonically increasing sequence of subharmonic functions that are even

64 3. Existence Techniques I: Methods Based on the Maximum Principle

harmonic in B(y,R). By the Harnack convergence theorem (Corollary 1.2.10),

the sequence (¯v

) converges uniformly on B(y, R)towardssomev that is

harmonic on B(y, R). Furthermore,

lim

n→∞

¯v

(y)=v(y)=u(y), (3.2.2)

since u ≥ ¯v

≥ v

and lim

n→∞

(y)=u(y). By (3.2.1), we then have v ≤ u

in B(y, R). We now show that v ≡ u in B(y, R). Namely, if

v(z) <u(z)forsomez ∈ B(y, R), (3.2.3)

by (3.2.1), we may ﬁnd ˜u ∈ S

with

v(z) < ˜u(z). (3.2.4)

Now let

:= max(v

, ˜u). (3.2.5)

In the same manner as above, by the Harnack convergence theorem (Corol-

lary 1.2.10), ¯w

converges uniformly on B(y,R)towardssomew that is har-

monic on B(y,R). Since w

≥ v

and w

∈ S

, the maximum principle

implies

v ≤ w ≤ u in B(y,R). (3.2.6)

By (3.2.2) we then have

w(y)=v(y), (3.2.7)

and with the help of the strong maximum principle for harmonic functions

(Corollary 1.2.3), we conclude that

w ≡ v in B(y, R). (3.2.8)

This is a contradiction, because by (3.2.4),

w(z) = lim

n→∞

¯w

(z) = lim

n→∞

max(v

(z), ˜u(z)) ≥ ˜u(z) >v(z)=w(z).

Therefore, u is harmonic in Ω. 

Theorem 3.2.1 tells us that we obtain a harmonic function by taking the

supremum of all subfunctions of a bounded function y. It is not clear at all,

however, that the boundary values of u coincide with y.Thus,wenowwish

to study the question of when the function u(x):=sup

v∈S

v(x) satisﬁes

lim

x→ξ∈∂Ω

u(x)=ϕ(ξ).

For that purpose, we shall need the concept of a barrier.

3.2 The Perron Method 65

Deﬁnition 3.2.3: (a) Let ξ ∈ ∂Ω. A function β ∈ C

(Ω) is called a barrier

at ξ with respect to Ω if

(i) β>0 in

Ω \{ξ}; β(ξ)=0,

(ii) β is superharmonic in Ω.

(b) ξ ∈ ∂Ω is called regular if there exists a barrier β at ξ with respect to Ω.

Remark: The regularity is a local property of the boundary ∂Ω:Letβ be a

local barrier at ξ ∈ ∂Ω; i.e., there exists an open neighborhood U(ξ)such

that β is a barrier at ξ with respect to U ∩ Ω.IfthenB(ξ, ρ) ⊂⊂ U and

m := inf

U\B(ξ,ρ)

β,then

β :=



m for x ∈

Ω \B(ξ, ρ),

min(m, β(x)) for x ∈

Ω ∩B(ξ, ρ),

is a barrier at ξ with respect to Ω.

Lemma 3.2.2: Suppose u(x):=sup

v∈S

v(x) in Ω.Ifξ is a regular point

of ∂Ω,andϕ is continuous at ξ, we have

lim

x→ξ

u(x)=ϕ(ξ). (3.2.9)

Proof: Let M := sup

∂Ω

|ϕ|.Sinceξ is regular, there exists a barrier β,and

the continuity of y at ξ implies that for every ε>0 there exists δ>0anda

constant c = c(ε) such that

|ϕ(x) − ϕ(ξ)| <ε for |x − ξ| <δ, (3.2.10)

cβ(x) ≥ 2M for |x − ξ|≥δ (3.2.11)

(the latter holds, since inf

|x−ξ|≥δ

β(x)=:m>0 by deﬁnition of β). The

functions

ϕ(ξ)+ε + cβ(x),

ϕ(ξ) − ε − cβ(x),

then are super- and subfamilies, respectively, with respect to ϕ, by (3.2.10),

(3.2.11). By deﬁnition of u thus

ϕ(ξ) − ε − cβ(x) ≤ u(x),

and since superfunctions dominate subfunctions, we also have

u(x) ≤ ϕ(ξ)+ε + cβ(x).

Hence, altogether,

|u(x) − ϕ(ξ)|≤ε + cβ(x). (3.2.12)

Since lim

x→ξ

β(x) = 0, it follows that lim

x→ξ

u(x)=ϕ(ξ). 

66 3. Existence Techniques I: Methods Based on the Maximum Principle

Theorem 3.2.2: Let Ω ⊂ R

be bounded. The Dirichlet problem

Δu =0 in Ω,

u = ϕ on ∂Ω,

is solvable for all continuous boundary values ϕ if and only if all points ξ ∈ ∂Ω

are regular.

Proof: If ϕ is continuous and ∂Ω is regular, then u := sup

v∈S

v solves the

Dirichlet problem by Theorem 3.2.2. Conversely, if the Dirichlet problem is

solvable for all continuous boundary values, we consider ξ ∈ ∂Ω and ϕ(x):=

|x − ξ|. The solution u of the Dirichlet problem for that ϕ ∈ C

(∂Ω)thenisa

barrier at ξ with respect to Ω,sinceu(ξ)=ϕ(ξ) = 0 and since min

∂Ω

ϕ(x)=

0, by the strong maximum principle u(x) > 0, so that ξ is regular. 

3.3 The Alternating Method of H.A. Schwarz

The idea of the alternating method consists in deducing the solvability of the

Dirichlet problem on a union Ω

∪ Ω

from the solvability of the Dirichlet

problems on Ω

and Ω

. Of course, only the case Ω

∩ Ω

= ∅ is of interest

here.

In order to exhibit the idea, we ﬁrst assume that we are able to solve the

Dirichlet problem on Ω

and Ω

for arbitrary piecewise continuous boundary

data without worrying whether or how the boundary values are assumed at

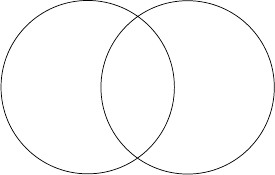
their points of discontinuity. We shall need the following notation (see Figure

3.2):

∗

:= ∂Ω

∩ Ω

:= ∂Ω

∩ Ω

:= ∂Ω

\ γ

:= ∂Ω

\ γ

∗

:= Ω

∩ Ω

Figure 3.2.

Then ∂Ω = Γ

∪ Γ

, and since we wish to consider sets Ω

,Ω

that are

overlapping, we assume ∂Ω

∗

= γ

∪γ

∪(Γ

∩Γ

). Thus, let boundary values

ϕ by given on ∂Ω = Γ

∪ Γ

. We put

:= ϕ|

(i =1, 2),

m := inf

∂Ω

ϕ,

M := sup

∂Ω

ϕ.