Jenkins N., Strbac G., Ekanayake J. Distributed Generation

Подождите немного. Документ загружается.

A resistor in one side (primary or secondary) of the transformer circuit can be

referred to the other side by equating the energy dissipated in them as heat. For

example, the heat loss associated with R

(on the primary side) is I

. If that

resistor is transferred to the secondary side an equivalent resistance is R

, then:

¼ I



ðIV:5Þ

Substituting for the current ratio from (IV.4) into (IV.5):



ðIV:6Þ

The primary leakage reactance may also be referred to the secondary side in a

similar manner:



ðIV:7Þ

Typically, the current through the magnetising branch of a transformer (X

and R

) is only about 3–5% of the full-load current. Therefore when considering a

loaded transformer, the magnetising branch is usually omitted. The equivalent

circuit of a loaded transformer where all the quantities are referred to the secondary

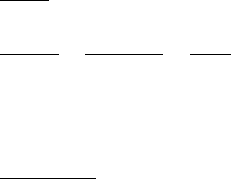
is shown in Figure IV.4.

Ideal

transformer

Figure IV.4 Simplified circuit of a transformer

In Figure IV.4:

¼R



¼X



ðIV:8Þ

The windings of practical power transformers are usually tapped to allow

alteration of the number of turns in use and hence the turns ratio of the transformer.

Power systems 247

In this way the secondary voltage may be altered (with a constant primary voltage).

On load tap changers use a combination of diverter and selector switches to change

the transformer ratio while it passes current and is on load (Figure IV.5). Off load tap

changers can be operated with voltage on the transformer (but no current flowing),

while off circuit tap changers can only be operated when the transformer is isolated.

Transformer windings Arrangement typically used fo

chan

transformer taps

Taps taken out

for the tap

changer

connection

Figure IV.5 Transformer winding and tap changing arrangement

EXAMPLE IV.1

A 50 kVA transformer has 400 turns on the primary and 40 turns on the

secondary. The primary and secondary resistances are 0.3 W and 0.01 W

respectively, and the corresponding leakage reactances are j1.1 W and j0.035

W respectively. Calculate the equivalent impedance referred to the primary.

Answer:

Since the resistance and reactance are transformed from the secondary to the

primary, the transformation is based on the square of the primary to sec-

ondary turns ratio, thus if the equivalent impedance referred to the primary is

þ jX

¼ R



¼ 0:3 þ

400



0:01

¼ 1:3 W

¼ X



¼ 1:1 þ

400



0:035

¼ 4:6 W

248 Distributed generation

IV.3 Per-unit system

The power system has multiple voltage levels from 765 kV, down to 400 V or even

120 V and this makes circuit analysis rather confusing. By converting all the

quantities into dimensionless quantities, known as per-unit (pu) quantities, it is much

easier to analyse the power system. The pu quantity of any value is defined as the

ratio between the actual value of the quantity and the base or reference value in

the same unit. The per-unit system avoids confusion with transformers, where the

impedance of transformers depends on the side from which it is viewed, and elim-

inates the factor of

ﬃﬃﬃ

involved in line and phase voltage and current quantities. The

per-unit normalisation applies only to magnitudes and angles are not normalised.

The per-unit calculation starts with defining base values for power system

quantities. First, choose one base power (VA) for the entire power system being

studied. This value is arbitrarily chosen, normally appropriate for the size of the

system (a common choice for a large power system is 100 MVA). Second, one base

voltage is chosen for each voltage level. Usually this is the nominal voltage on each

side of the transformers; defined by the nominal turns ratio of the transformer.

Finally, other base values are calculated to get the same relationship between per-

unit quantities as between actual quantities.

For a distributed generator calculation, a suitable MVA base, S

, is first cho-

sen. The line-to-line voltages, V

, of the various voltage levels are selected as the

voltage bases (V

). The current and impedance base are then obtained as:

ﬃﬃﬃ

ðIV:9Þ

ﬃﬃﬃ

½V



ðIV:10Þ

For example, if V

= 33 kV and S

= 100 MVA, Z

is given by:

ð33  10

100  10

¼ 10 :86 W

IV.3.1 Power transformers in per unit

For three-phase transformers in a power system, the resistances are much smaller

than reactances. Therefore, the per-phase transformer equivalent circuit shown in

Figure IV.4 is simplified by neglecting the resistance (Figure IV.6).

For a transformer two base voltages are defined: primary voltage, V

, and the

secondary voltage, V

From Figure IV.6:

¼ V

ðIV:11Þ

¼ V

þ jI

ðIV:12Þ

Power systems 249

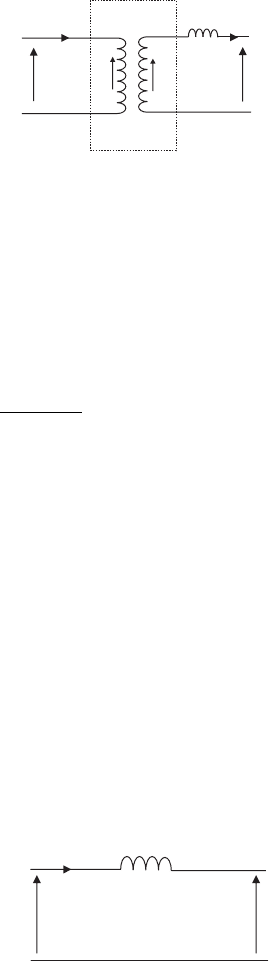
By dividing (IV.11) by V

ﬃﬃﬃ

(as the equation is a per-phase equation):

1;pu

¼ V

1;pu

¼ 1pu ðIV:13Þ

Similarly by dividing (IV.12) by V

ﬃﬃﬃ

2;pu

¼ V

2;pu

ðV

ﬃﬃﬃ

¼ 1pu ðIV:14Þ

From (IV.9) and (IV.10):

¼ V

ﬃﬃﬃ

ðIV:15Þ

Therefore, (IV.14) was rewritten as:

2;pu

¼ V

2;pu

þ jI

2;pu

L;pu

¼ 1pu ðIV:16Þ

From (IV.13) and (IV.16):

1;pu

¼ V

2;pu

þ jI

2;pu

L;pu

ðIV:17Þ

Therefore, the transformer is represen ted by the equivalent circuit shown in

Figure IV.7 in per unit.

, pu

1, pu

2, pu

1, pu

Figure IV.7 Transformer equivalent circuit in pu

The equivale nt leakage reactance of the transformer, X

, is normally defined

as a percentage on its own name-plate rating. For example a transformer impedance

of 6% on a 1 MVA transformer is simply: X

= 0.06 pu, S

= 1 MVA.

Ideal

transforme

Figure IV.6 A simplified circuit of a power transformer

250 Distributed generation

IV.3.2 Generators

As discussed in Tutorial II, a generator also has an internal impedance where the

resistive component is very small compared to the inductive component. The

internal impedance of the generat or is generally represented by a percentage, which

is the internal reactance in pu on the machine base multiplied by 100.

IV.3.3 System studies

To study a system using the pu system, all quantities are expressed in a consistent

manner, that is on the same base power for the whole syst em being studied and the

same base voltage for all the components at a voltage level. In many case s, the

impedances of the transformers and generators are given on their own name-plate VA

bases. It is then necessary to convert these impedances into the common system base.

Assume that a pu impedance, Z

, is given on a power base of S

. If the ohmic

value of the impedance is Z. Then from (IV.10):

¼ Z 

ðIV:18Þ

The impedance Z can be translated to a per unit impedance, Z

, on a power

base of S

as:

¼ Z 

ðIV:19Þ

From (IV.18) and (IV.19):

¼ Z



ðIV:20Þ

EXAMPLE IV.2

Using a 10 MVA base, change all the parameters in the following circuit into

per unit and draw the simplified equivalent circuit.

12.5:33 kV

15 MVA

15%

Distribution line

impedance = 10 + j 50 Ω

12.5 kV

10 MVA

35%

Answer:

Assume voltage bases of: 12.5 kV for the primary side of the transformer and

33 kV for the secondary side of the transformer.

On 10 MVA base, the generator reactance is 35% = j 0.35 pu.

The transformer impedance is equal to j 0.15 pu on a 15 MVA base.

From (IV.20), on a 10 MVA base it is equal to j 0.15  10/15 = j 0.1 pu.

Power systems 251

On 33 kV, 10 MVA, the base impedance is given by: Z

= (33  10

)

10  10

= 108.6 W

The per unit impedance of the distribution line is (10 þ j50)/108.6 =

0.092 þ j0.46 pu.

Then system in pu is drawn as:

0.092 +

0.46 1 pu

j 0.1

i 0.35

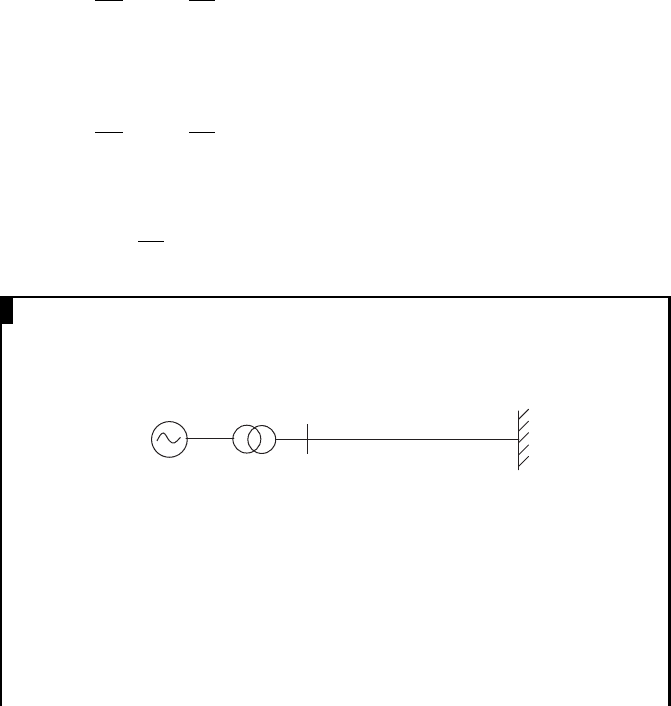
EXAMPLE IV.3

A schematic diagram of a radial network with a distributed generator is

shown here. Calculate the terminal voltage of the synchronous generator if

the voltage at busbar A at 30 kV. Use a 100 MVA base.

11:132 kV

50 MVA

X = 10%

132:33 kV

50 MVA

X = 12%

j 50 Ω

25 MW

0.8 pf lagging

Busbar A

Answer:

On V

= 132 kV and S

= 100 MVA, Z

is given by:

ð132  10

100  10

¼ 174: 24 W

The 11:132 kV transformer impedance on 100 MVA base = j0.1  (100/

50) = j0.2 pu.

The 132:33 kV transformer impedance on 100 MVA base = j0.12 

(100/50) = j0.24 pu.

The line impedance (j 50 W) on 132 kV, 100 MVA base = j50/174.24 =

j0.287 pu.

Since cos f = 0.8, f = 36.87



Therefore, reactive power absorbed by the main system = (25/cos f) 

sin f = (25/0.8)  0.6. = 18.75 MVAr

Load power in pu = (P þjQ)/S

= (25 þ j18.75)/100 = 0.25 þ j0.1875 pu.

As the voltage at busbar A is 30 kV, on a 33 kV base it is 30/33 pu =

0.909 pu. Defining this voltage as the reference voltage:



¼ 0:25 þ j0:1875

0:909  I



¼ 0:25 þ j0:1875

¼ 0:275  j0:206

252 Distributed generation

See Figure I.13 in Tutorial I.

Now for the radial distribution system, the following equation was written

in pu:

¼ V

þI

 jð0:2 þ 0:24 þ 0:287Þ

¼ 0:909 þð0:275  j0:206Þj0:727

¼ 0:909 þ 0:15 þ j0:2

¼ 1:059 þ j0:2

¼ 1:08ﬀ10:7



On the 11 kV base, the generator terminal voltage = 1.08 11 = 11.88 kV.

IV.4 Symmetrical components

A three-phase system operating under balanced, symmetrical conditions was dis-

cussed in Tutorial I. However, unsymmetrical conditions often occur in the power

system due to unbalanced loading and asymmetrical faults (line–ground, line–line,

etc.). In order to analyse the power system under unsymmetrical conditions, the

system of symmetrical components is used. The basis is that any set of unbalanced

three-phase voltages or currents can be represented by three balanced sets of pha-

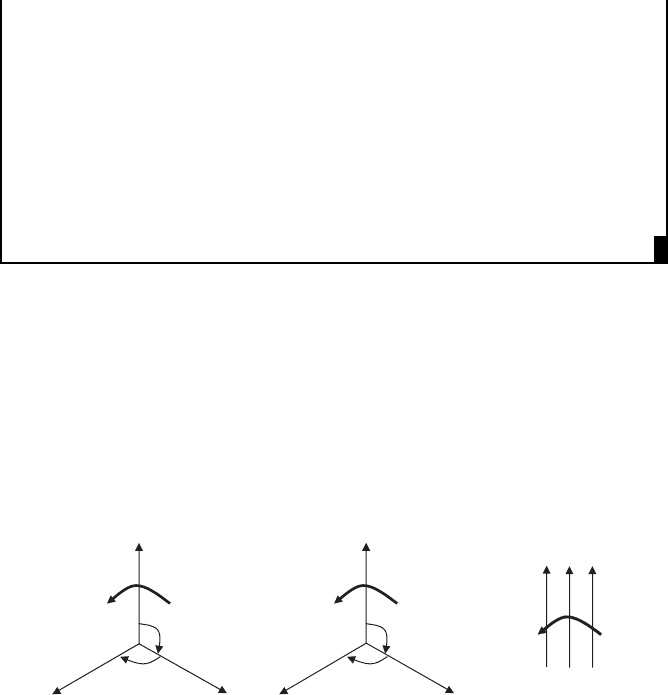
sors – positive, negative and zero – as shown in Figure IV.8.

The positive sequence phasor voltages have the same phase sequence

(ABC)

as the three-phase electrical power system. If the phase sequence of three voltages

is ACB, then these voltage components are called the negative sequence compo-

nents. The components where three voltages are equal in magnitude and phase are

called zero sequence components.

The phasor representation of the zero sequence voltages (subscript 0 refers to

zero sequence):

¼ V

ﬀ0



¼ V

 e

ðIV:21Þ

(

)

Positive sequence

(

)

ative sequence

(

)

Zero sequence

120°

Figure IV.8 Phasor representation of a three-phase voltage system

Power systems 253

The phasor representation of the positive sequence voltages (subscript 1 refers

to positive sequence):

¼ V

ﬀ0



¼ V

 e

¼ V

ﬀ120



¼ V

 e

j2p=3

¼ V

 e

j4p=3

¼ V

ﬀ240



¼ V

 e

j4p=3

¼ V

 e

j2p=3

ðIV:22Þ

Let l = e

j2p/3

, then:

¼ V

 l

¼ V

 l

ðIV:23Þ

The phasor representation of the negative sequence voltages (subscript 2 refers

to the negative sequence):

¼ V

ﬀ0



¼ V

 e

¼ V

ﬀ240



¼ V

 e

j4p=3

¼ V

 e

j2p=3

¼ V

ﬀ120



¼ V

 e

j2p=3

¼ V

 e

j4p=3

ðIV:24Þ

Then:

¼ V

 l

¼ V

 l

ðIV:25Þ

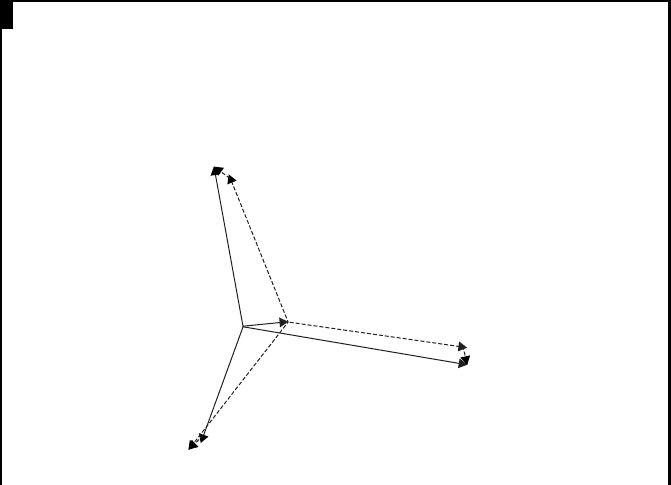
EXAMPLE IV.4

Using a phasor diagram show that the three unbalanced currents I

200 ﬀ 10



, I

= 250 ﬀ100



and I

= 150 ﬀ200



can be represented by the

addition of positive, negative and zero sequence currents.

Answer:

= I

254 Distributed generation

As shown in the above diagram, the unbalanced currents can be repre-

sented by the addition of positive sequence currents (dashed lines) having a

magnitude of 196 A, where I

leads I

by 22



, negative sequence currents

(dotted lines) having a magnitude of 19 A, where I

leads I

by 57



, and

zero sequence currents (solid lines) having a magnitude of 54 A, where I

lags I

by 85



As any unbalanced set of three-phase voltages or currents can be represented

by the addition of the zero, positive and negative sequence voltage or currents, for

voltages:

¼ðV

þ V

¼ðV

þ V

þV

¼ðV

þ V

þV

ðIV:26Þ

Equation (IV.26) was rewritten by substituting from (IV.21), (IV.23) and

(IV.25):

¼ðV

þ V

¼ðV

þ l

þ lV

¼ðV

þ lV

þ l

ðIV:27Þ

In matrix form:

11 1

1 l

1 ll

ðIV:28Þ

If V

, V

and V

are known then the three sequence component may be

found by:

11 1

1 l

1 ll

1

ðIV:29Þ

In order to find the inverse of

11 1

1 l

1 ll

;

11 1

1 l

1 ll



11 1

1 ll

1 l

Power systems 255

is considered:

11 1

1 l

1 ll

11 1

1 ll

1 l

3 ð1 þl þl

Þð1 þl þl

ð1 þl þl

Þð1 þ2l

Þð1 þl

þl

ð1 þl þl

Þð1 þl

þl

Þð1 þ2l

ðIV:30Þ

Figure IV.9 shows how phasors are rotated with the l operator. From the figure it

may be seen that (1 þ l þ l

) = 0, (1 þ 2l

) = 3 and (1 þ l

þ l

)=0.

␭

Figure IV.9 l operator

From (IV.30):

11 1

1 l

1 ll



11 1

1 ll

1 l

¼ 3 

100

010

001

ðIV:31Þ

Therefore from matrix algebra:

11 1

1 l

1 ll

1

11 1

1 ll

1 l

ðIV:32Þ

Thus from (IV.29):

11 1

1 ll

1 l

ðIV:33Þ

IV.5 Problems

1. A single-phase transformer has a primary/secondary turns ratio of 0.5. The

total resistance and reactance referred to the secondary side are 2.5 W and 10 W

[A]  [B] = 3[I], [A]  [B]/[A] = 3[I]/[A], [B] = 3[A]

1

, [A]

1

= 1/3[B]

256 Distributed generation