Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


528
CHAPTER
9.
STOCHASTIC
MODELING
Now,
let us
consider
the
family
F"
of
realizations generated
by a BBS
using
the n first
realizations contained,
for
example,
in the
family
5-'.
Generally, this
new
family
of
equiprobable realizations
is
such
that
In
other words,
the BBS
generates equiprobable realizations
that
neither
a
SGS
nor a
P-field-based
simulator
can
generate. Consequently,
one can say
that
the BBS
really generates
new
equiprobable realizations.
9.9
Assessing
geometric
uncertainties
In
this section,
two
examples
will
show
how
stochastic simulators
can
also
be
used
for
assessing uncertainties
of
geometric objects.
9.9.1
Example
1:
Case
of a
discrete
model
Let
G
be a
]>dimensional
geometric object embedded
in the
IR
m
space
and
whose
unknown
geometry
(x(u)
6
]R
m
}
is a
function
of a
parameter
u
itself
defined
on a
region
D of
]R
P
called
the
"parametric
domain:"
Let us now
consider
a
discrete model
A^
m
(r2,7V,
x,
C)
approximating
the un-
known
geometry
{x(u)
6
M
m
}
of G. At
each node
a
e
0,
the
parameter
u(a)
is
assumed
to be
known
and
x(a)
is
assumed
to be an
approximation
of
the
unknown
value
x(u(a)):
It
should
be
observed
that
the
interpolation
{x(a)
: a 6 fi} of
x(u)
gener-
ated
by the
DSI
method must
be
considered
as an
estimate
of the
unknown
geometry
[153].
To
assess
the
uncertainties regarding
the
geometry
of G, we
propose building
a
geometric simulator
X(u,
u;)
having
the
following
form:
Note
that
it is not
mandatory
for the
vectors
{v(a)
: a G
0}
to be
unit
vectors,
and the
construction
of
X(u,
u>)
can be
reduced
to the
construction
of
the
scalar simulator
5(u,u;).
In
practice,
it is
assumed
that
This
is
achieved
if
5(u,
u;)
is
constrained
to be
centered:

9.9.
ASSESSING GEOMETRIC
UNCERTAINTIES
Assuming
that
a
periodic
P-field
as
denned
in
section
(9.5.2)
is
used
to
build
the
simulator
5(u,c*;),
the
only parameter remaining
to be
chosen
is the co-
variance
function,
which controls
the
behavior
of
5(u,
u]
when
far
away
from
the
data
points.
Comment
1
Observe
that
equation
(9.170)
is
simply
a first-order
approximation
of the
following
general nonlinear model:
In
this equation,
{v(s
a) : a €
$1}
represents
a
given
family
of 3D
curves
parameterized
by
their
arc
length
s and
whose shapes must
be
chosen
as
functions
of the
geometry
of
G.
Note
that
it is
even possible
to
envision
a
more
general
stochastic
geometric simulator where
the
shapes
of
these
curves
are
themselves stochastic:
In
any
case, however,
it is
necessary
to
install some geometric constraints
to
avoid self-intersecting realizations
of the
geometric object
G.
Comment
2
In the
case where
the
geometric object
G is a
smooth surface
not too far
from
its
current approximation,
a
very simple stochastic geometric simulator
consists
in
choosing
v(u)
proportional
to an
approximation
of the
unit normal
vector
N(a)
to G at
point
X(U(CK)):
Choosing
the
orientation
of
v(o:)
this
way has the
advantage
of
being simple,
but
does
not
take into account
the
origin
of the
errors.
To
have
a
better
model,
it is
necessary
to
examine
the
modeling process used
for
building
the
first
draft
of G in
detail
(e.g.,
see
[49]).
Comment
3
If
it is
assumed
that
||v(o;)|
represents
the
maximum amplitude
of the
vari-
ation
of the
geometry
at
location
x(u(a)),
then
it is
wise
to
choose
C$
(h)
to
have:
It is
verifiable
that
any
centered normalized Gaussian Random Variable
has
a
0.95 probability
of
belonging
to the
interval
[—1.96,+1.96].
Consequently,
if
a
Gaussian simulator
is
used, then
from
this
observation,
the
choice
guarantees
that
^(u,^)!
will
remain lower
than
1
with
a
probability greater
than
0.95.
529
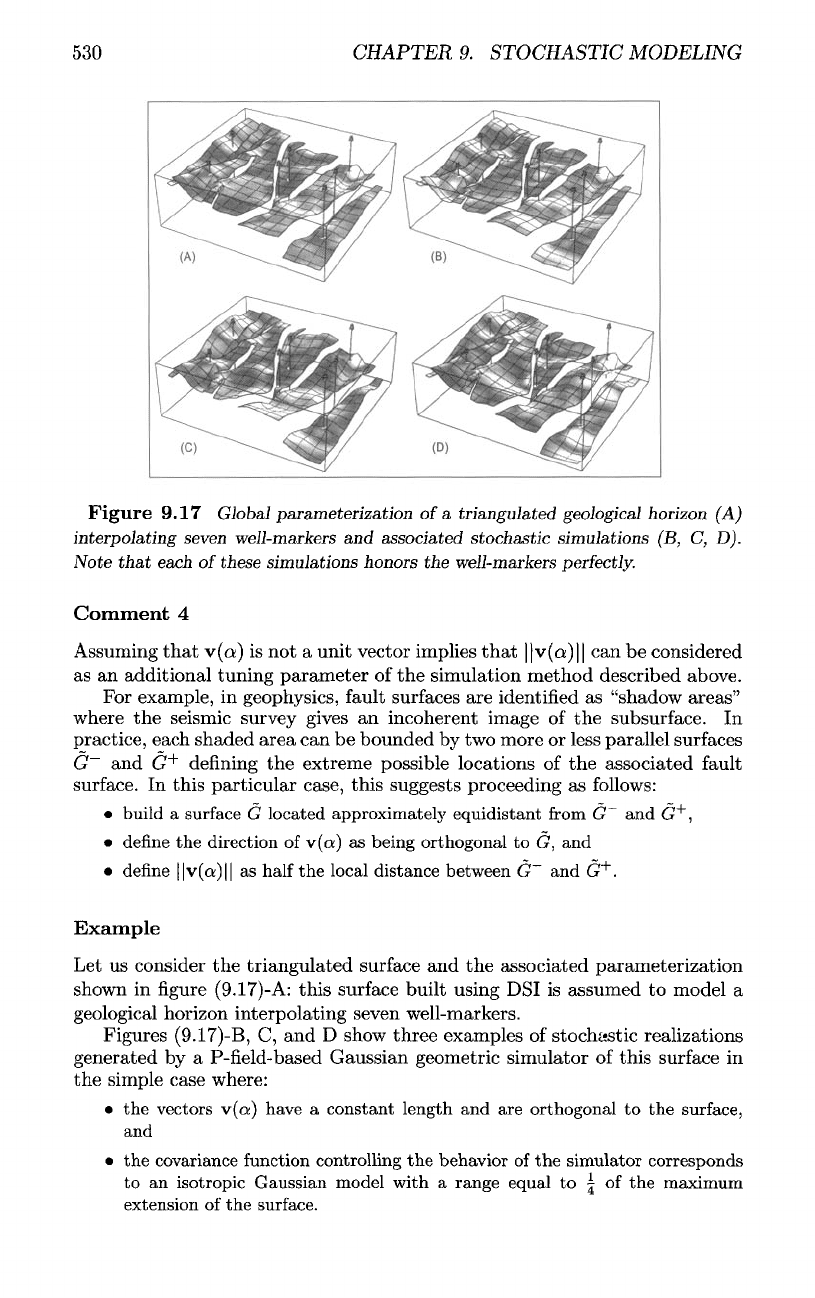
530
CHAPTER
9.
STOCHASTIC MODELING
Figure
9.17
Global
parameterization
of
a
triangulated
geological
horizon
(A)
interpolating
seven
well-markers
and
associated
stochastic
simulations
(B, C, D).
Note
that
each
of
these
simulations
honors
the
well-markers
perfectly.
Comment
4
Assuming
that
v(a)
is not a
unit vector implies
that
11v(a)
11
can be
considered
as an
additional tuning parameter
of the
simulation method described above.
For
example,
in
geophysics,
fault
surfaces
are
identified
as
"shadow
areas"
where
the
seismic survey gives
an
incoherent image
of the
subsurface.
In
practice,
each shaded area
can be
bounded
by two
more
or
less parallel surfaces
G~
and
G
+
defining
the
extreme possible locations
of the
associated
fault
surface.
In
this particular case, this suggests proceeding
as
follows:
•
build
a
surface
G
located
approximately
equidistant
from
G~
and
G
+
,
•
define
the
direction
of
v(a)
as
being
orthogonal
to G, and
•
define
||v(a)||
as
half
the
local
distance
between
G~
and
G
+
.
Example
Let
us
consider
the
triangulated surface
and the
associated parameterization
shown
in figure
(9.17)-A:
this
surface
built using
DSI
is
assumed
to
model
a
geological
horizon interpolating seven well-markers.
Figures
(9.17)-B,
C, and D
show three examples
of
stochastic realizations
generated
by a
P-field-based
Gaussian geometric simulator
of
this surface
in
the
simple case where:
• the
vectors
v(a)
have
a
constant
length
and are
orthogonal
to the
surface,
and
• the
covariance
function
controlling
the
behavior
of the
simulator corresponds
to
an
isotropic
Gaussian
model
with
a
range
equal
to
|
of
the
maximum
extension
of the
surface.

9.9.
ASSESSING GEOMETRIC UNCERTAINTIES
531
Figure
9.18
Stochastic
simulations
of
channels
interpolating
six
well-markers.
Note
that
each
of
these
simulations
honors
the
well-markers
perfectly.
9.9.2
Example
2:
Channels simulator
When characterizing heterogeneities
of fluviatile
reservoirs,
one is
often
faced
with
the
problem
of
channel
facies
observed
on
well
logs
but not
visible
in
the
seismic
data
[234,
222].
In
such
a
situation,
a
stochastic
simulator must
be
built
and
must
be
capable
of
generating
the
geometry
of
possible channels
that
honor
the
well
data.
For
simplicity's sake,
let us
assume
that
• the
channels
have
to be
generated
in a (u, v)
parametric
space
such
that
the
stream
directions
correspond
to the u
direction;
• the
wells
can
intersect
the
channels
at
randomly
simulated
locations
relative
to
centerlines.
According
to
such hypotheses,
the
centerline
of the
channel
to be
generated
can be
seen
as the
realization
of a
random
function
v
=
S(u,
u;).
We
propose
to
build
a
sequential simulator constrained
to
honor
a
series
of
points
{(iti,Vi)
:
«
=
!,...,
AT}
corresponding
to the
intersection
of the
wells with
the
channel.
In
this case,
the
range
of the
covariance
function
Cs(h)
to be
used must
be
chosen
as
being equal
to
half
the
wave length
of the
meanders (see
[186]).
Such
an
approach gives good results
but
suffers
from
one
drawback:
the
shape
of the
meanders does
not
look
like
the
real centerline
of
channels. Sec-
tion (5.6.1) shows
how
this drawback
can be
overcome (see
figures
(5.16)
and
(9.18))
thanks
to a
postprocessing based
on the
curvature
of the
centerline
of
each
channel.
In
practice
and as
shown
in
figure
(9.18),
the
(u,v}
parametric space
is
chosen
as a map of a
channel belt
on a
paleo-horizon
during
a
given geological
time
lag
(i±At)
corresponding
to the
segments
of
channel
facies
intersected
by
the
wells. Proceeding
in
this
way
guarantees
that
the
channels
so
generated
will
remain approximately
in the
channels' belt
if the
covariance
function
Cs(h]
is
chosen such
as
where
Ai>
represents
the
width
of the
channel belt
in the
parametric space.
As
shown
in figures
(9.18)
and
(9.19),
the (u, v)
parametric space
can be
viewed

532
CHAPTER
9.
STOCHASTIC MODELING
Figure
9.19
The
(u,v,w)
parametric
space
represented
in figure
(9.18)
can be
used
to
parameterize
a
faulted/folded
regular curvilinear
3-grid
modeling
a
geological
layer
(see
also
figures
5.16
and
3.18).
as a
slice
of the
(w,
u,
w)
parametric space used
for
parameterizing
a
regular
curvilinear
3-grid modeling
a
faulted/folded layer.
The
geometry
of
such
a
curvilinear
3-grid
can
also
be
denned
to fit the
shape
of the
channel
belt.
9.10
Conclusions
This
chapter presented
a
series
of
stochastic
methods generating equiprob-
able
solutions
of
interpolation problems.
In
practice, these methods
can be
combined
to
randomize both
the
geometry
and the
properties
of
geological
structures. Such
an
approach makes
it
possible
to
scan
a
large number
of
pos-
sible
solutions honoring
the
available
data.
These
solutions
can be
used
in two
different
ways
for
evaluating uncertainties
on
economic
parameters
controlling
the
decision-making process:
•
First,
it is
possible
to use
these solutions
for
building histograms
of
economic
parameters, depending
on the
geometry
and the
properties
of the
subsurface.
•
Next,
it is
possible
to
examine each
of
these solutions
in
turn
to
determine
whether there
are
some catastrophic occurrences where
the
geometry
and the
distribution
of
physical properties jeopardize
the
economic exploitation
of an
oil
field or an ore
deposit.
If
such occurrences
do
exist, then
it is of
paramount
importance
to
look
for
additional
data
to
confirm
or
reject
it.
It
should
be
noted, however,
that
while
these methods
allow
an
evaluation
of
the
uncertainties, they
are
(generally) unable
to
predict their origin.

Chapter
m
Discrete
Smooth
Partition
In a
broad
sense,
a
fades
in
geology
represents
a
part
of
the
subsurface
where
a
given
set
of
properties
can be
considered
as
more
or
less
constant
at a
given
scale.
Each fades
can be
composed
of
a
series
of
non-overlapping
regions,
and
the set
of
all the
possible
fades
constitutes
a
partition
of the
subsurface.
To
estimate such
a
partition, this
chapter
proposes
a new
approach
that
is
based
on
the
DSI
method
and
that takes into account
a
wide
range
of
structural
constraints
allowing
the
space
of the
possible solutions
to be
reduced.
By
definition,
any
partition obtained
using
this method
will
be
called
a
"Discrete
Smooth Partition."
10.1
Introduction
10.1.1
The
classification
problem
Notion
of
classification
In a
general way,
it can be
said
that
any
classification
problem consists
in
splitting
a set
0
into
a
series
of
non-overlapping subsets
{F
1
,...,F
n
},
called
the
"classes"
defining
a
partition
of
Q.
Such
a
definition
can be
applied
to
very
different
types
of
problems,
for
example,
1. in
sociology,
if
$7
represents
a
population
of
individuals, then each class
F"
may
correspond
to a
social class;
2.
in
paleontology,
if
f2
represents
the
family
of
dinosaurs, then each class
F"
represents
a
different
breed
of
dinosaurs;
3.
in
geology,
if
fJ
represents
a
part
of a
geological layer
(see
figure
(10.1)),
then each class
F"
corresponds
to a
given type
of
rock, called
the
"fades,"
533

534
CHAPTER
10.
DISCRETE
SMOOTH
PARTITION
Figure
10.1
Partitioning
the set
fi
of
all
the
3-cells
of
a
(cell-centered)
curvilinear
regular
3-grid
into
n
subsets corresponding
to a
given series
of
geological
fades
{.F
1
,..
.,F
n
}.
For the
sake
of
clarity,
in the
vertical direction, only
one
cell
out of
four
has
been
displayed
and the
altitudes have been multiplied
by a
factor
of 5.
(Data
courtesy
of
Chevron)
contained
in
this layer;
and
4.
in
environmental sciences,
if fi
represents
a
region
on the
surface
of the
earth,
then each class
F
v
may
correspond
to an
ecosystem present
in
this area.
One
of the
very
first to
take
a
scientific
approach
to
classification
problems
was
Linnee
who,
in the mid
18th
century,
proposed
the first
classification
of flowers.
In the
statistical
community,
there
is a
long
tradition
of
works
dedicated
to
"discriminant"
and
"clustering"
methods.
In
1936,
Fisher
[79]
posed
the
problem
in
mathematical
terms,
and,
since
this
date,
a
great
deal
of
literature
has
been
dedicated
to
this
topic.
All
these
methods
assume
that
each
element
of
fi is
characterized
by a
series
of
numerical
and/or
non-numerical
attributes
used
for
detecting
similarities
and
dissimilarities
between
these
elements.
In
practice,
two
generations
of
such
methods
can be
distinguished:
• A first
generation
of
methods, introduced
in the
1970s,
is
based
on the
notion
of
"metrics" used
to
define
similarities
and
dissimilarities
in
term
of
distances
or
pseudo-distances
in the
space
of the
observed attributes.
A
survey
of
these
methods
can be
found
in
[11,
83,
203,
103,113,
189, 126]
can
also
be
mentioned.
• A
second generation
of
methods, introduced
in the
1980s,
is
based
on the no-
tion
of
"neural networks." Compared
to
their previous generation, these meth-
ods
represent
a
major improvement because they
are
nonlinear and, within
the
space
of the
observed parameters, they permit
the
building
of
complex
shaped classes.
A
survey
of
these methods
can be
found
in
[104].
Note also
that
a
method close
to
neural networks
is
proposed
in
section (10.4).

10.1. INTRODUCTION
535
Specificity
of
geometric objects
It is
important
to
note
that
none
of the
traditional
statistical
methods distin-
guishes
between attributes corresponding
to the
location
of the
elements
of
f2
in
space
and
attributes
corresponding
to the
properties
of
these elements.
This strategy
of
clustering
is
certainly valid
for
examples
(1) and (2)
men-
tioned
in the
above paragraph,
but
fails
completely
for
examples
(3) and (4)
where
the
location
of the
elements
of fi
relative
to
each other plays
a
major
role. Compared
to
classic property attributes,
it can be
said
that
location
attributes have
a
totally
different
role
for the
following
reasons:
• two
elements
of
fi
can
belong
to the
same
class
F
v
even
if
they
are
very
distant
from
each
other
in
space,
and
• the
distribution
and the
shapes
of the
classes
{F
l
,...,F
n
}
in
space
must
honor
structural
information,
if
any, related
to the
geometric
shape
of
these
classes.
Traditional
statistical
methods
are
unable
to
take into account
the
specific
nature
of
attributes corresponding
to the
location
of the
elements
of
fi.
For
this reason,
a new
geostatistical approach
to
this problem (Indicator Kriging
[116,
117, 118, 199,
188])
has
been proposed; this approach makes
a
clear
dis-
tinction between
the
property attribute(s)
z(a)
and the
location attribute(s)
u(a)
of
each element
a G
£1.
This chapter presents
a
similar approach based
on
the
Discrete Smooth Interpolation
(DSI)
method
that
allows
a
large spec-
trum
of
structural information
to be
taken into account related
to the
shape
and the
distribution
of the
subsets
{jP
1
,...,
F
n
}
over
the set
17.
10.1.2
Discrete partition
of a
geometrical
object
Notion
of
facies
As
suggested
in figure
(1.5)
and
(10.1),
any
geometrical object
can be
approx-
imated
by a
graph
1
C/(f2,
JV)
where:
•
O
is the set of all the
nodes
of the
graph.
•
N(-)
is an
application
used
for
specifying
the
"neighborhood"
N(a)
of any
node
a
G
fi.
In
this chapter,
as
suggested
in figure
(10.1),
it is
assumed
that
each node
a G
O
consists
of a
homogeneous
n-cell
where
non-geometrical
attributes
2
are
more
or
less constant.
Most
of the
time,
the set
17
is not
homogeneous
and it is
necessary
to
split
it
into
a
family
F
of n
different
regions
F
v
called
the
"facies" where
non-geometrical attributes
can be
considered approximately constant:
the
node
a of
$1
belongs
to the
facies
#
v
1
See
chapter
1,
page
5.
2
For
example,
in
geology,
n = 2 or 3 and
these attributes
may
correspond
to
numerical
properties
such
as
permeability
or
porosity,
and
non-numerical
properties,
such
as
type
of
rock
and
presence
of
oil, attached
to the
cells.

536
CHAPTER
10.
DISCRETE SMOOTH PARTITION
The
family
T
so
defined
constitutes
a
partition
of
f);
this
is
equivalent
to say
that
The
problem
addressed
in
this
chapter
The
partition
F
is
generally unknown
and its
intersection with
a
given subset
L of
fi
is the
only
exact
information available:
There
is, of
course,
an
infinite
set of
partitions
J-
honoring
the
data
set L,
and the
goal
of
this chapter
is to
propose
a
method allowing such partitions
to be
built, while honoring some constraints.
In
particular,
we are
looking
for
"structured" solutions having
the two
following
properties:
1.
If a
node
a is in a
fades
F",
then
it is
highly
probable
that
its
neighboring
nodes
(3 G
N(a)
will
belong
to the
same
facies
F".
In
other
words,
we are
looking
for a
"smooth" partition.
2.
The
proportions
of the
different
facies
and the
transitions
from
one
facies
to
another
should
honor
some
structural
constraints
[91,
195].
It
will
be
shown
how the
DSI
method
can be
used
for
building solutions
honoring both
of
these goals,
and we
propose calling
"Discrete
Smooth
Partition"
(DSP),
the
family
J-~
so
obtained.
Tutorial
geological
example
In
figure
(10.1)
a
geological layer
is
modeled
as a
cell-centered curvilinear
regular 3-grid
£(fi,
N)
where
the set
fi
has
been split into
n
facies
induced
by
non-numerical
geological
attributes:
a €
F
1
•<=>•
a
belongs
to the
"shalestone"
geological
facies
a G F
2
•<=>•
a
belongs
to the
"carbonate"
geological
facies
a G
F
3
<4=>-
a
belongs
to the
"sandstone"
geological
facies
a G
F
n
<=$•
a
belongs
to the
"conglomerate"
geological
facies
The
geometry
of the
curvilinear regular 3-grid
is
chosen
to
cope with
the
sedimentation process
in
such
a way
that
the
curvilinear axis noted
as
(u,
v,
w)
can be
interpreted
as
follows:
• w
corresponds
to the
"paleo-vertical"
direction
orthogonal
to the
layer,
and it
is
implicitly
assumed
that
there
is an
unknown
monotonic
increasing
function
t =
t(w)
linking
the
geological
time
t to
w;
•
(it,
v)
correspond
to the
"pseudo-horizontal"
surface
parallel
to the
layer
and
are
interpreted
as the
"paleo-geographic
coordinates"
at
geological
deposition
time
t =
t(w).

10.1.
Figur e
10.2
Tutorial example:
the
initial data consist
of a set
of
four
poros-
ity
classes
{Fl,
F
2
,
F
3
,
F
4
}
observed
on
eleven well-paths
plus
a
regular curvilin-
ear
3-grid
on
which
the
seismic amplitudes have been reported. (Data courtesy
of
Chevron)
In
practice,
the
facies
{F
1
,...,
F
n
}
are
only known
on a set L of
nodes located
on
the
well-paths
and
have
to be
estimated
on
O
to
interpolate
L,
while taking
into account additional structural information such
as
• a
seismic amplitude observed everywhere
in the
layer,
•
horizontal average proportion
maps
3
of
facies,
•
vertical average proportion
curves
4
of
facies,
and
•
macro
sequences
5
of
transgressions
and
regressions
of the sea
level.
Figure
(10.2)
shows
a
real
data
set
consisting
of
• a set of
eleven wells along which
the
facies crossed
by the
well-paths
are
given,
and
• a
seismic amplitude given
at
every node
of the
grid.
In the
realm
of
geosciences, curvilinear regular 3-grids
are
often
used because
of
the
natural interpretation
of the
w
direction
as
geological time
and the
(w,
v)
as
paleo-geographic
coordinates. Consequently, throughout this chapter most
of
the figures
refer
to
this kind
of
mesh,
but it
should
be
noted
that,
except
in
a few
particular
cases,
6
any
kind
of
graph
£7(O,
AT)
can be
used
for
modeling
the
topology
of the
domain
to be
partitioned.
3
A
function
of
(it,u).
4
A
function
of
w.
5
A
function
of
w.
6
For
example,
in
sections
(10.3.4)
and
(10.3.5), taking into
account anisotropies
and
gradients
does
not
require
a
regular 3-grid.
537
