Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

558
CHAPTER
10.
DISCRETE SMOOTH PARTITION
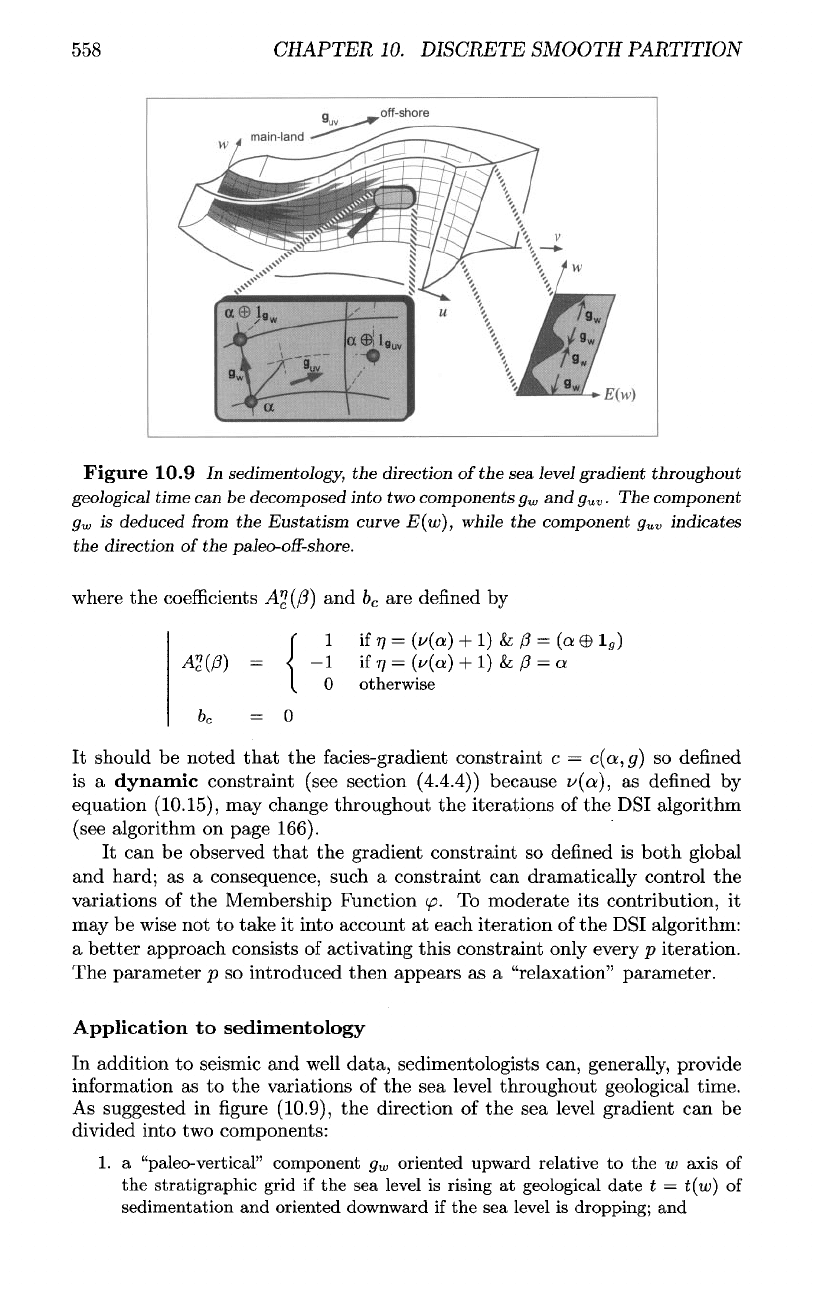
Figure
10.9
In
sedimentology,
the
direction
of
the sea
level
gradient
throughout
geological
time
can be
decomposed
into
two
components
g
w
and
g
uv
.
The
component
g
w
is
deduced
from
the
Eustatism
curve
E(w),
while
the
component
g
uv
indicates
the
direction
of the
paleo-off-shore.
where
the
coefficients
A^(j3)
and
b
c
are
denned
by
A209)
=
if
77
=
(i/(a)
+ 1) & (3 = (a
0
1<
if
j]
=
(i/(a)
+ 1) &
/3
= a
otherwise
= 0
It
should
be
noted
that
the
facies-gradient constraint
c =
c(a,g)
so
defined
is
a
dynamic
constraint (see section
(4.4.4))
because
i'(a),
as
defined
by
equation (10.15),
may
change throughout
the
iterations
of the
DSI
algorithm
(see
algorithm
on
page 166).
It can be
observed
that
the
gradient constraint
so
denned
is
both global
and
hard;
as a
consequence, such
a
constraint
can
dramatically control
the
variations
of the
Membership Function
(p. To
moderate
its
contribution,
it
may
be
wise
not to
take
it
into account
at
each iteration
of the DSI
algorithm:
a
better
approach consists
of
activating
this
constraint only every
p
iteration.
The
parameter
p so
introduced then appears
as a
"relaxation" parameter.
Application
to
sedimentology
In
addition
to
seismic
and
well
data,
sedimentologists can, generally, provide
information
as to the
variations
of the sea
level throughout geological time.
As
suggested
in
figure
(10.9),
the
direction
of the sea
level gradient
can be
divided
into
two
components:
1.
a
"paleo-vertical"
component
g
w
oriented
upward
relative
to the
w
axis
of
the
stratigraphic
grid
if the sea
level
is
rising
at
geological
date
t =
t(w)
of
sedimentation
and
oriented
downward
if the sea
level
is
dropping;
and
1
1
0
b

10.4. MOVING-CENTERS-BASED METHODS
559
2.
a
"paleo-horizontal"
component
g
uv
parallel
to the
(u,v)
horizons
and
indi-
cating,
globally,
the
direction
of the
off-shore
at the
time
of
sedimentation.
One
or two of
these components
may be
given
by the
sedimentologist,
at
least
on
a
subset
A of
f2.
In
practice,
the
vertical
component
g
w
is
deduced
from
the
derivative
of a
curve
E(w],
called
an
"Eustatism
curve," describing
the
variations
in the sea
level
as a
function
of
w.
The
derivative
of
this curve
is
assumed
to
have
the
same sign
as the
derivative
of the sea
level
at
geological
time
22
t =
t(w)
so
that
g
w
can be
deduced
as
follows:
g
w
oriented
upward
g
w
oriented
downward
As
suggested
in
figure
(10.9),
the two
components
g
w
and/or
g
uv
can be
used
for
denning
gradient constraints
on
nodes
a 6 A of the
discrete model used
for
modeling
the
subsurface.
Application
to
paleo-channel
modeling
As
suggested
in figure
(3.18),
let us
consider
a
stratigraphic grid
filling a
paleo-channel.
As
usual,
it is
good
practice
to
adjust
the
orientation
of the
curvilinear axis
(it,
v,
w) as a
function
of the
main parameters which controlled
the
sedimentation
at the
time
of
deposition (see
[200]).
For
example,
let us
assume
that
these curvilinear axes
are
oriented
as
follows:
• the u
axis
is
oriented
radially
from
the
left
bank
to the
right
bank,
• the v
axis
corresponds
to the
orientation
of the
paleo-stream-tubes,
and
• the w
axis
corresponds
to the
paleo-vertical.
Due
to the
shape
of the
meanders
and the
shape
of the
section
of the
channel,
the
cells
do not
have
a
constant size
in the
(it,
w)
cross sections
and
this cells
can be
calibrated
to be
such
that
•
small
cells
correspond
to
small
intensities
of the
paleo-flow,
and
•
large
cells
correspond
to
large
intensities
of the
paleo-flow.
The
intensity
of the
paleo-flow
controls
the
granulometry.
It may be
wise
to
use the
gradient
of the
size
of the
cells
as a
DSI
constraint
to be
applied
to
the
Membership Function
of the
facies corresponding
to
different
classes
of
granulometry.
10.4
Moving-Centers-based
methods
This section presents
a
very simple traditional method used
in
data
analysis
for
partitioning
a set £ of
elements characterized
by a
vector
of
attributes
X(e)
observed
for any e G
£.
It
will
also
be
shown
that
this method
can
easily
be
adapted
to
•
estimate,
in a
nonlinear
way,
a
property
Y(e)
in
function
of the
observation
X(e)
realized
on
each
element
e 6
£,
and
22
It
is
implicitly
assumed that dt/dw
>
0 for any
value
of w.
560
CHAPTER
10.
DISCRETE SMOOTH PARTITION
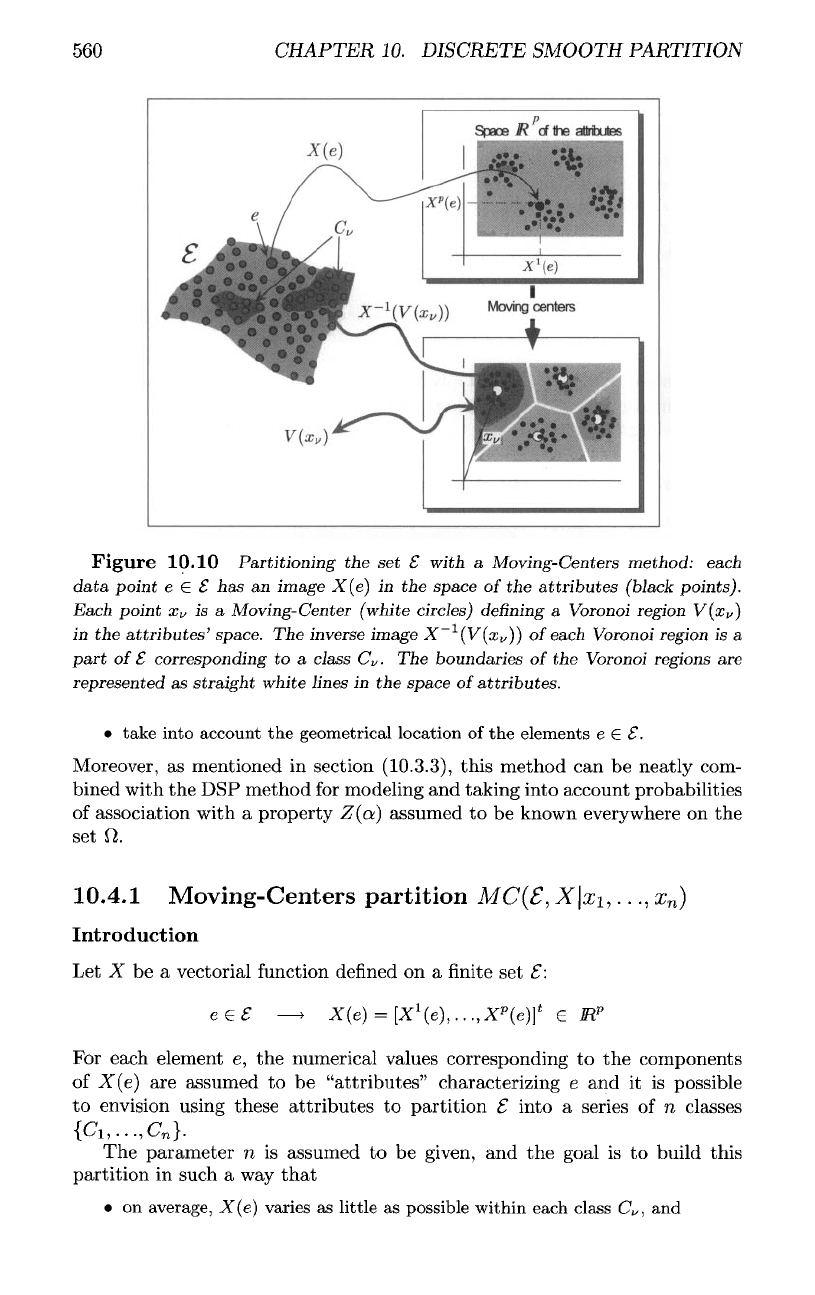
Figure
10.10
Partitioning
the set 8
with
a
Moving-Centers
method:
each
data
point
e
e
8 has an
image
X(e)
in the
space
of
the
attributes
(black
points).
Each
point
#„
is a
Moving-Center
(white
circles)
denning
a
Voronoi
region
V(x
v
)
in the
attributes'
space.
The
inverse
image
X~
l
(V(x
v
}}
of
each
Voronoi
region
is a
part
of
£
corresponding
to a
class
C
v
.
The
boundaries
of the
Voronoi
regions
are
represented
as
straight
white
lines
in the
space
of
attributes.
•
take
into
account
the
geometrical
location
of the
elements
e G
£.
Moreover,
as
mentioned
in
section (10.3.3), this method
can be
neatly
com-
bined with
the DSP
method
for
modeling
and
taking into account probabilities
of
association with
a
property
Z(a)
assumed
to be
known everywhere
on the
set
J7.
10.4.1
Moving-Centers
partition
MC(£,
X\x\,...,
x
n
)
Introduction
Let
X be a
vectorial
function
denned
on a finite set E:
For
each element
e, the
numerical values corresponding
to the
components
of
X(e)
are
assumed
to be
"attributes" characterizing
e and it is
possible
to
envision using these attributes
to
partition
8
into
a
series
of
n
classes
{Ci,..
.,C
n
}.
The
parameter
n is
assumed
to be
given,
and the
goal
is to
build this
partition
in
such
a way
that
• on
average,
X(e)
varies
as
little
as
possible
within
each
class
CV,
and

10.4. MOVING-CENTERS-BASED
• on
average,
(X(e),X(e)}
should
be, as far as
possible,
different
if e and
e
belong
to two
different
classes.
As
suggested
in
figure
(10.10),
to
solve this problem,
it is
assumed that,
ir
the
attributes's space
JR
P
',
the
image
X(C
V
]
of
each class
is
fully
containec
in
a
Voronoi region
(see
definition
(3.2)
page
99)
V(x
v
]
centered
on a
poinl
x
v
E
M
p
.
In
other words, each
of the
centers
{x
v
:
v =
1,..
.,n}
defines
i
class
C
v
as
follows:
The
"Moving-Centers"
method
in a
nutshell
As
shown
in
figure
(10.10),
the
image
X(£)
of £ in the
attributes' space
fit?
consists
of a
"cloud"
of \£\
points.
Let k be an
iteration counter;
to any
giver
set
of
n
"centers"
xl
belonging
to
JR
P
,
it is
possible
to
associate
a
partition
X\-
k
-
of
X(£]
as
defined
by
with:
Any
initial given partition
X^
of
M
p
can
always
be
improved thanks
to
the
"Moving-Centers" method
[83, 126, 59],
which corresponds
to the
following
iterative algorithm:
//—
Moving-Centers
algorithm
let {
x\
,...,
x
n
} be an
arbitrary initial
set of
points
of
JR
P
let k
<-
0
while(
more iterations
are
needed
) {
let
X^
be the
partition
associated
with
{
x\
,...,
Xn
}
for_all(
v €
[l,n]
) {
•
xH?
+l]
=
center
of
gravity
of
x}f
]
}
•
k<-k
+ l
}
As
can be
seen
in
figure
(10.11),
at
each
iteration,
the
centers
{x
v
}
move
to £
new
location, giving this algorithm
its
name:
the
"Moving-Centers" method
This algorithm
is
proven
to be
convergent,
23
and the
series
of
partitions
{A^}
so
obtained
has the
following
interesting properties
[126]:
• If
Wv
is
denned
as the
"within" dispersion
of
class
Xc,
at
iteration
k
23
In
practice,
it
converges
very
rapidly.
561
562
CHAPTER
10.
DISCRETE SMOOTH PARTITION
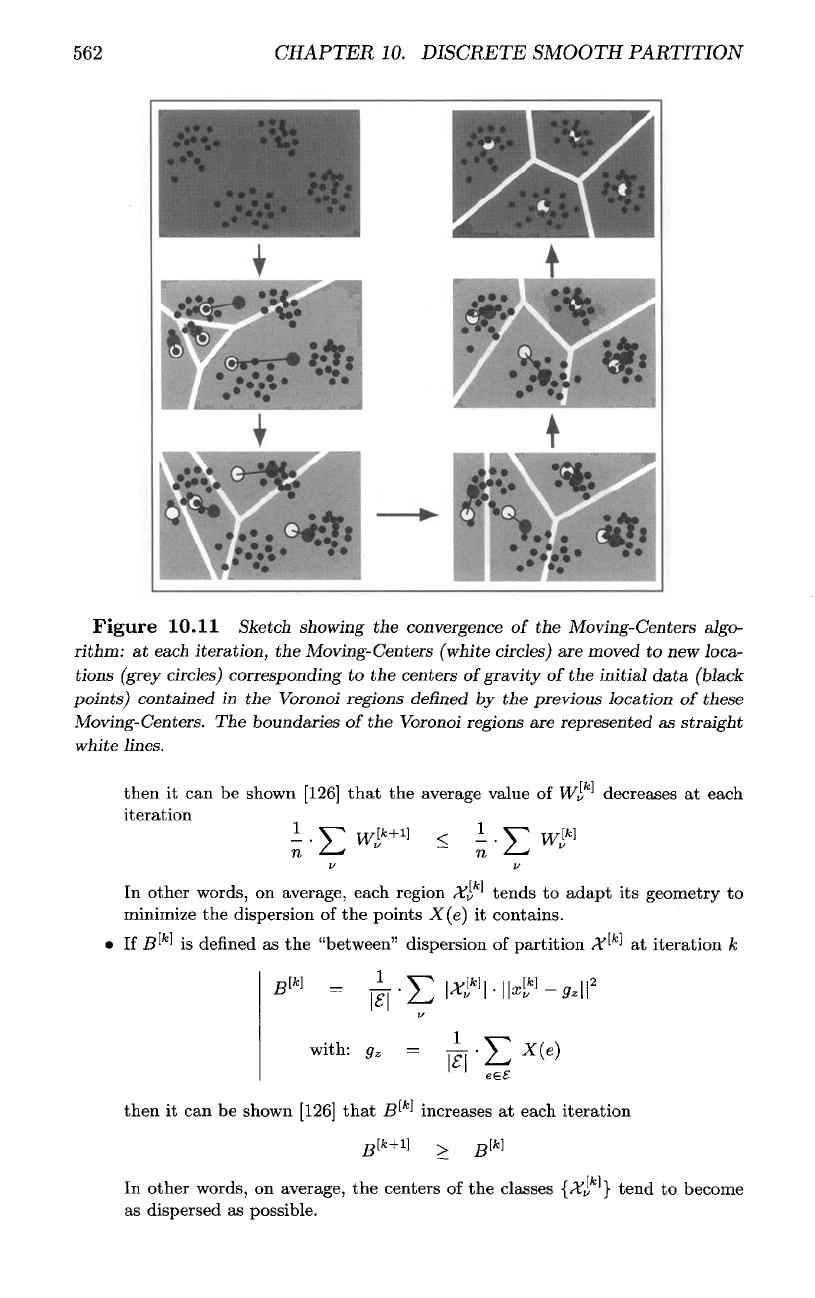
Figure
10.11 Sketch showing
the
convergence
of the
Moving-Centers
algo-
rithm:
at
each
iteration,
the
Moving-Centers (white
circles)
are
moved
to new
loca-
tions
(grey
circles)
corresponding
to the
centers
of
gravity
of
the
initial data (black
points) contained
in the
Voronoi
regions
defined
by the
previous location
of
these
Moving-Centers.
The
boundaries
of
the
Voronoi
regions
are
represented
as
straight
white lines.
then
it can be
shown [126]
that
the
average value
of
Wl
decreases
at
each
iteration
In
other words,
on
average, each region
X»
tends
to
adapt
its
geometry
to
minimize
the
dispersion
of the
points
X(e)
it
contains.
• If
B^
is
defined
as the
"between" dispersion
of
partition
X^
at
iteration
k
then
it can be
shown [126]
that
B^
increases
at
each iteration
In
other words,
on
average,
the
centers
of the
classes
{Xl
}
tend
to
become
as
dispersed
as
possible.

10.4
As
shown
in figures
(10.10)
and
(10.11),
the
classes
{X^}
so
defined
are
delim-
ited
by
convex polyhedral
divisions
of
JR
P
formed
by the
median hyperplanes
of
the
segments joining
all the
center pairs.
Notations
Prom
now on, the
following
notation
will
be
used
to
designate
a set of n
classes
{Ci,...,
C
n
}
generated
by the
Moving-Centers
algorithm based
on the
function
X
defined
on the set 8 and
using
an
initial
set of
centers
{x\,...,
x
n
}:
For
simplicity's sake,
in the following, two
implicit assumptions
will
be
made:
• If a
class becomes empty during
the
iterative Moving-Centers algorithm, then
the
largest class
is
split into
two
classes.
As a
consequence,
the
classes gener-
ated
by the
Moving-Centers method
are
never empty.
• In the
notation
MC(S,X\xi,..
.,x
n
),
the
initial
Moving-Centers
{xi,..
.,£
n
},
given
as
input
of the
method,
are
assumed
to be
replaced
by the
centers
that
define
the
classes generated
by the
method:
In
other words, although this
is not at all
recommended
in
software
design,
the
algorithm
MC(£,
X\x\,..
.,x
n
)
is
assumed
to
modify
its
input arguments
{#i,..
,,x
n
}.
From
a
theoretical point
of
view,
the
following
more rigorous,
but
cumbersome, notations would
be
preferable:
MC(£,X
|*i,...,4
;
z!..,4)
where
the
{xl}
are the new
centers generated
as
outputs
by the
algorithm,
while
the
{xl}
are its
inputs.
Non-uniqueness
of the
solution
It
should
be
noted
that
the
Moving-Centers method does
not
generate only
one
solution:
the
partition
MC(£,
X\xi,...,
x
n
]
depends, theoretically,
on the
number
and
location
of the
initial centers
{x\,...,
x
n
}
given
as
input.
In
practice, however,
for a
given number
of
centers
n, the
classes generated
by
different
sets
of
initial Moving-Centers
are
pretty
similar.
Therefore,
a
series
of n
points
{x
v
=
X(e
v
}}
randomly selected among
the
images
{X(e)
:
e
€
£}
is
generally chosen
as the
initial
set
{#1,..
.,x
n
}.
As can be
seen
in
figure
(10.11),
in the
case where
the
images
of the
classes
in the
attributes'
space
are
well
individualized,
the
partition generated
by the
Moving-Centers
method retrieves these classes
and,
in
practice, does
not
actually depend
on
the
location
of the
initial centers.
Preprocessing
of the
data
The
method presented above implicitly assumes
that
the
components
of
X(e)
are
chosen
in a
consistent
way.
In
particular,
the
following
possible problems
have
to be
taken into account:
563
56

564
CHAPTER
10.
DISCRETE
SMOOTH
PARTITION
• The p
components
of
X(e)
may
correspond
to
heterogeneous physical param-
eters having very
different
orders
of
magnitude. This
may
have
a
detrimental
effect
on the
metric
|| •
\\JRP
of the
attributes' space:
in
this case, components
of
X(e)
having
the
largest order
of
variation
will
completely override
the
effect
of
the
other components.
•
Even
in the
case where
the
components
of
X(e)
are of the
same type,
it is
unavoidable
that
some
of
these components
may be
redundant (e.g., corre-
lated):
in
this case, redundant variables
will
also tend
to
override
the
effect
of
the
other components.
•
Most
of the
time,
the
components
of
X(e)
correspond
to
experiments
affected
by
measurement errors:
in
this case,
the
experimental errors
will
also tend
to
corrupt
the
distances between
the
elements
of the set £.
The
following
procedure
provides
an
excellent
technique
for
avoiding
all
these
problems:
1.
Compute
the
principal
components
24
of the raw
data
{X*(e)
:
e
G
£}
corre-
sponding
to
experimental measurements.
2.
Choose
as
{X(e)
:
e €
8}
the first p
principal components explaining
80% of
the
data
variance.
In
practice,
such
a
preprocessing
generates
excellent
results.
10.4.2
Estimating
a
function
There
are
many
situations
where
a
function
X(e)
is
known
for
each
element
e
E £ of a
given
set
£,
while
a
second
function
Y(e)
is
known only
on a
subset
8*
of £
called
the
"learning
set."
In
such
a
case,
using
the
"links"
between
Y and X for
estimating
Y(e)
everywhere
on
(£
—
£*)
can be
envisioned.
For
example,
if
X(e)
represents
a
seismic
amplitude
25
observed
at
each
node
e of
a
seismic
cube
£,
then
Y(e)
observed
at
well
locations
e €
£*
crossing
the
seismic
cube
may be
• the
porosity:
in
this case,
Y(e)
is
assumed
to be a
continuous
function
taking
its
values
within
the
range
[0,1];
• a
porosity class:
in
this case,
Y(e)
is
assumed
to be an
integer
function
taking
its
values within
the set
{1,2,...,
m}
in
such
a way
that
Y(e)
= i if e has a
porosity belonging
to
class
}yi-i,yi}',
• the
index
of a
geological facies:
in
this
case,
Y(e)
is
assumed
to be an
integer
function
taking
its
values within
the set
(1,2,...,
m};
• the
presence
or
absence
of a
given geological
facies:
in
this case,
Y(e)
is
assumed
to be a
Boolean
function
taking
one of the two
values
0 or 1;
• the dip of the
layers:
in
this case,
Y(e)
is
assumed
to be a
continuous vectorial
function
taking
its
values
on the
unit sphere
of
JR
3
.
Generally
the
"links"
if
any,
are
very
complex,
and it is
illusory
to
look
for
one
single
value
Y(e)
=
f(X(e}}
attached
to
each
node
e 6 £.
Assume
that
24
For
a
complete
presentation
of
Principal Component Analysis (PCA),
the
reader
is, for
example, referred
to
[126].
25
X(e)
could also represent
the
invariants
of the
strain
tensor computed
as
indicated
in
section (8.6.7).
10.4.
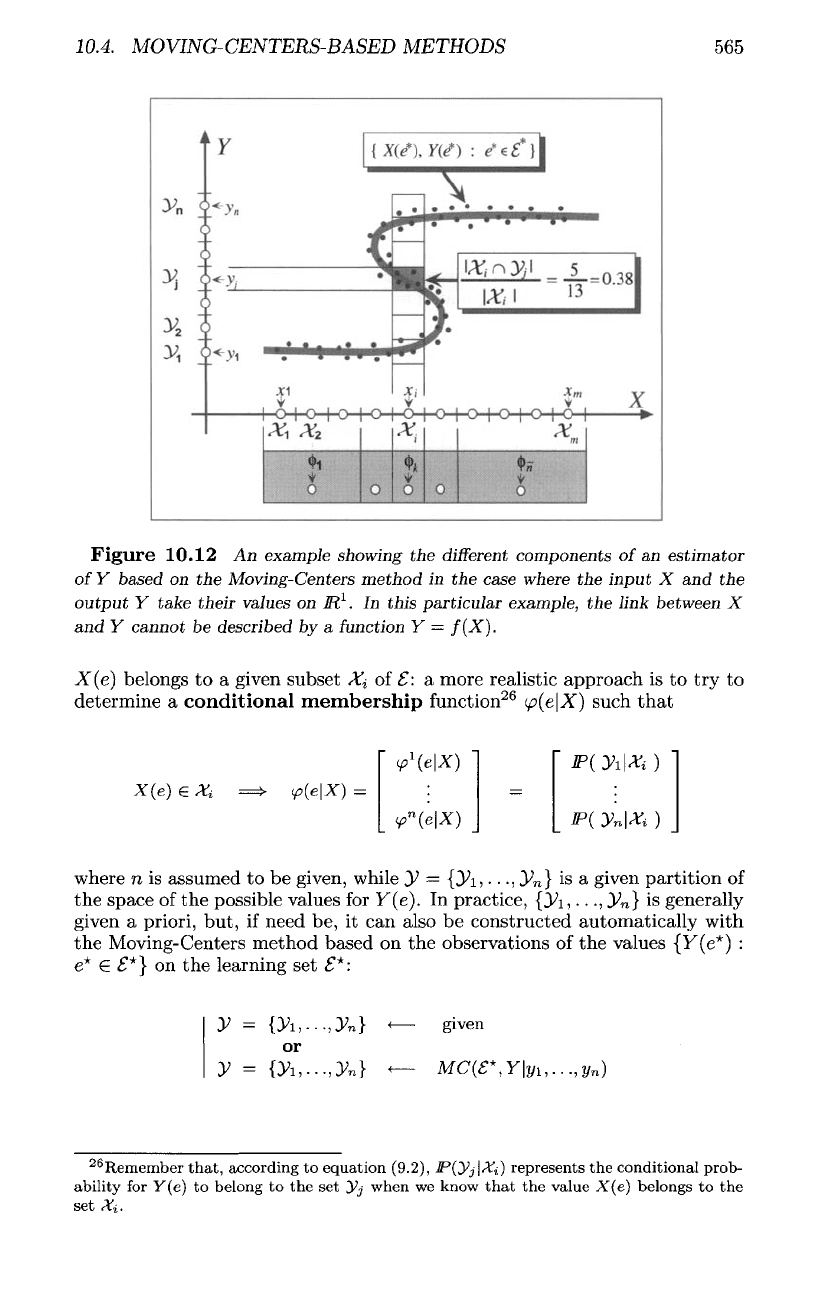
Figure 10.12
An
example showing
the
different
components
of an
estimator
of
Y
based
on the
Moving-Centers
method
in the
case
where
the
input
X and the
output
Y
take their
values
on
M
1
.
In
this particular example,
the
link between
X
and
Y
cannot
be
described
by a
function
Y =
f(X).
X(e)
belongs
to a
given subset
Xi
of
S:
a
more realistic approach
is to try to
determine
a
conditional membership
function
26
(p(e\X)
such
that
where
n is
assumed
to be
given, while
y —
{3^i,
• • •,
y
n
}
is a
given
partition
of
the
space
of the
possible values
for
Y(e).
In
practice,
(3^,...,
y
n
}
is
generally
given
a
priori,
but,
if
need
be, it can
also
be
constructed
automatically
with
the
Moving-Centers
method
based
on the
observations
of the
values
{Y(e*}
:
e*
6 £*} on the
learning
set
8*:
26
Remember
that, according
to
equation
(9.2),
JPQ^IAfj)
represents
the
conditional prob-
ability
for
Y(e)
to
belong
to the set yj
when
we
know
that
the
value
X(e)
belongs
to the
set
Xi.
565

566
CHAPTER
10.
DISCRETE
SMOOTH
PARTITION
A
first
solution based
on
Moving-Centers
First,
build
a
partition
X =
{Xi,...,
X
m
}
of the
learning
set 8*
based
on the
observations
of the
values
{X(e*)
:
e*
e
8*}:
As
suggested
in figure
(10.12),
using
the two
partitions
X and
3^,
for
each
e*
€ 8*
such
that
X(e*)
G
A'j,
the
components
of the
conditional
membership
function
27
(p(e*\X)
can be
estimated
as
follows:
Next,
as
illustrated
in the
lower
part
of figure
(10.13),
it is
proposed
to use the
centers
{#1,..
.,x
m
}
and
their
associated
Voronoi
regions
{V(ori),...,
V(x
m
)}
for
extending
this
estimation
of the
components
of
(p(e\X)
as
follows
on the
whole
set 8
where
X(e)
is
known:
A
better solution based
on
Moving-Centers
One
can
consider
the
estimation
method
presented
above
as a
"black
box"
with
m
inputs
and n
outputs:
• TO
represents
the
number
of
different
Voronoi
regions
of
the
attributes'
space
that
one
wants
to
take into account
as
input
of the
proposed estimation
method. Ideally, choosing
a
large value
for
TO
would seem
to be
ideal
to
make
this method
as
discriminant
as
possible.
However,
correct estimation
of the
probabilities
\Xi
Cl
3^
|/1<-fi|
requires
TO not to be too
large
to
have enough
points
X(e*)
in
each class
Xi.
• n
represents
the
number
of
different
classes
of
values
of
Y(e)
to be
generated
as
output
of the
proposed estimation technique.
The
value
of n is
generally
determined
as a
function
of the
application,
but
must remain small
to
have
enough points
in
each
set Xi
fl
3^-
to
estimate
the
probabilities
\Xi
Pi
3
/
j|/|<
;
ki|
correctly.
Let
us
assume
that
n has
been
chosen;
as
illustrated
in figure
(10.12)
and in
the
upper
part
of figure
(10.13),
a
three-step
algorithm
is
proposed
to
improve
the
estimation
of the
Membership
Function
(p
defined
by
equation
(10.18):
1.
Using
the
images
(y(e*)
:
e* 6
£*},
choose
or
build
a
partition
y =
{^i,..
.,3^}
of
the
learning
set S*
denning
the
output
of the
method:
27
In
other words,
y>i(e*\X)
is the
conditional probability
of
y,-
relative
to the
fact
that
it is
known
that
X(e)
belongs
to Xi.
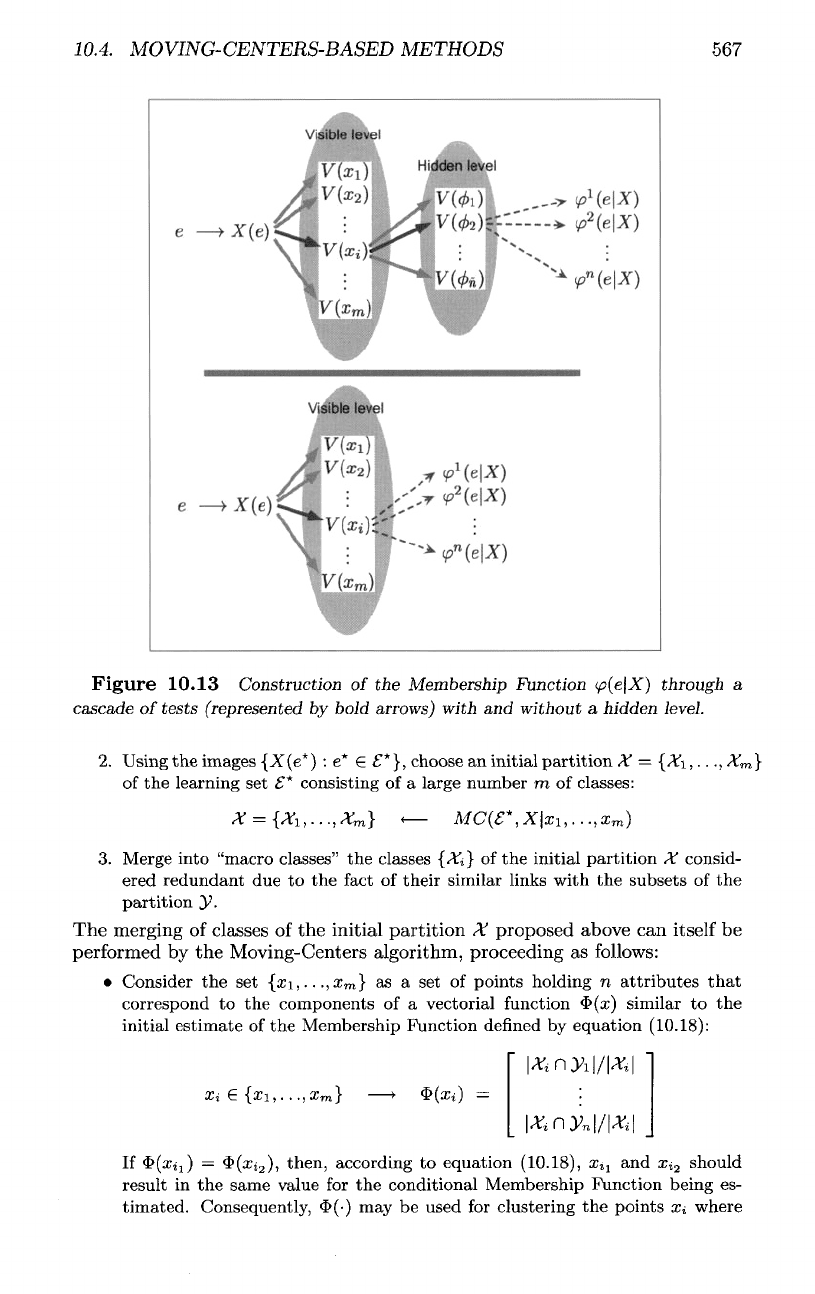
10.4.
MOVING-CENTERS-BASED
Figure 10.13
Construction
of the
Membership Function
<p(e\X)
through
a
cascade
of
tests
(represented
by
bold
arrows)
with
and
without
a
hidden level.
2.
Using
the
images
{X(e*)
:
e*
G
£*},
choose
an
initial
partition
X =
{Xi,...,
X
m
}
of
the
learning
set £*
consisting
of a
large number
m
of
classes:
3.
Merge into "macro classes"
the
classes
{Xi}
of the
initial partition
X
consid-
ered redundant
due to the
fact
of
their similar links with
the
subsets
of the
partition
y.
The
merging
of
classes
of the
initial
partition
X
proposed
above
can
itself
be
performed
by the
Moving-Centers
algorithm,
proceeding
as
follows:
•
Consider
the set
{xi,...,x
m
}
as a set of
points holding
n
attributes
that
correspond
to the
components
of a
vectorial
function
Q(x)
similar
to the
initial
estimate
of the
Membership Function
defined
by
equation (10.18):
If
$(xii)
=
$(xi
2
),
then, according
to
equation (10.18),
x^
and
Xi
2
should
result
in the
same value
for the
conditional Membership Function being
es-
timated. Consequently,
<&(•)
may be
used
for
clustering
the
points
Xi
where
56
