Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


178
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
•
choose
a
constraint
•
update
•
update
}
for_all(
c
e
C ) {
if(
c is
dynamic
) •
update
c
}
let
gradi
be the
vector
defined
by
equation
(4.59)
} // end :
while(
more
iterations
are
needed
)
It is
important
to
note that, contrary
to the
pure conjugate gradient method,
the
above algorithm allows
the
dynamic
and
hard constraints
to be
taken into
account
at
each step
of the
iterative process.
As a
consequence:
• if
there
is no
active
dynamic
and/or
hard
constraint
other
than those
corre-
sponding
to
C
L
,
then
the
above
algorithm
reduces
to the
classical
conjugate
gradient
method,
and
• if
there
are
active
dynamic
and/or
hard
constraints,
then
the
above
algorithm
is
equivalent
to the
classical
DSI
algorithm based
on the
local
form
of the
DSI
equation.
For
these
reasons,
we
propose calling
"pseudo"
Conjugate-Gradient
method
the
above algorithm derived
from
a
method initially proposed
by
Fletcher
and
Reeves [81]
for
minimizing non-quadratic objective
functions.
Computing
the
optimal
value
s
It can be
observed
that
the
above Pseudo-Conjugate-Gradient method
re-
quires
to
compute
the
optimal value
of s at
each
iteration.
Unfortunately,
if
there
are
active dynamic constraints,
the
matrix
[W//]
varies
at
each iteration
and the
pseudo-conjugate directions cannot rigorously honor
the
conjugacy
constraint (4.58):
as a
consequence, equation
(4.57)
cannot
be
used
to
deter-
mine
the
optimal value
of s. In
this section
we
will
show
how to
compute this
optimal value
as a
function
of the
terms
g
u
(oi),
G"(a\(p),
7"(en)
and
T
y
(ot\(f>)
denned
by
equations
(4.47),
and
(4.48).
For
this
purpose,
let us
consider
the
direction d as a vector of IRn' partitioned in a similar way to the partition
of
(p
denned
by
equation (4.30):
For the
sake
of
simplicity,
the (n •
|L|)
components
of
dL
are
assumed
to be
equal to zero and we introduce the vector x(s) of lRn' denned by

4.6.
ACCELERATING
THE
CONVERGENCE
179
Let
x
v
(a.,
s]
and
d
l
'(a)
be the
components
of
x(s)
and d
corresponding
to the
component
(p
v
(ot)
of
(f>:
Using
the
notations
presented
in
section (4.1.5),
we can
write
By
definition
of
R*(x),
we
have (see equation
(4.22)):
According
to
equation
(4.43),
and
(4.44),
we
also have:
Merging
these
two
equations with equation
(4.61)
gives:
Let
B
l>
(a\i/j)
and ft"(a) be the
real values
defined
as
follows
for any
node
a
e
ft and any
vector
^
e
M
n
'
M
:
On
the
other hand,

180
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
Using
these notations,
we
deduce
that
equation (4.62)
can be
written
as
According
to
equation
(4.60),
this implies:
The
optimum value
of s is
thus
the one for
which
dR*(x(s})/ds
is
equal
to
zero,
leading
us to
conclude
that
s
must
be
chosen such
that
where
B
V
(OL\I^)
and
b
v
(a)
are
defined
by
equations
(4.63).
4.6.2
Other acceleration
techniques
The
over relaxation
and
conjugate gradient methods
can be
combined with
other techniques
to
achieve even
faster
implementations
of the DSI
algorithm.
In the
following,
three
of
these possible methods
are
presented
briefly.
Fast
initializers
Fast
initializers
are
methods
that
allow
for the
rapid generation
of an
initial
solution
</?[o],
close
to the
optimal
DSI
solution.
For
example,
a
very
efficient
method,
called
the
"explosive
data
method"
(see
[50])
consists
in
propagating
a
"wavefront"
W(t)
from
the
initial
data
through iterations
t =
(0,1,...):
//—
explosive data
initializer
for DSI
let t
<—
0
let
£7(t)
<—
set of
nodes
holding Control-Nodes
let
W(t)
<—
fi(t)
while(fl(*)
^
ft ) {
W(t
+
!)<—0
for_all(
a 6
W(t)
) {
for_all(
13
€.
N(a)
) {
if(
(3 not in ft(t) ) {
•
¥>(£)
<—
¥>(«)
•
n(t)
<—
n(t)
u
{(3}
• W(t +
l)<—W(t
+
l}U{/3}
}
}
}

4.6.
ACCELERATING
THE
CONVERGENCE
I t is
easy
to
extend
this
algorithm
to
other
constraints
such
as
fuzzy
Control-
Nodes
or
fuzzy
Control-Points (see sections
(4.4.2),
and
(4.7)).
Multigrid
Methods
Multigrid
methods consist
in
decomposing
the
discrete model
.A/P(f2,
N,
(p,C]
into
a
series
of
simpler models defined
as
follows:
is
deduced
from
.M"(n[i_i],Ar[i_i],y>[i_i],C[i_i])
by
regularly
removing
nodes
from
O[j_i]
Let
us
assume
that
a
series
of
m
such models have been built
that
way.
The
interpolation
of
<f>
with
the
DSI
method
on
M
n
($l,
N,
(p,
C]
can be
greatly
ac-
celerated
by
using
the following
algorithm where
m is a
positive given integer:
//-
Multigrid algorithm
for DSI
for(
i = m ;
i>Q
;
i
) {
•
apply
DSI to
•
define
the
Control-Nodes
Ct
n
as
follows:
[i—ij
The
solution
<£>[Q]
s
°
obtained
can
then
be
used
as an
initial
solution
for the
DSI
algorithm applied
to
A4
n
(f2,
N,
ip,C).
The
principal
difficulty
with this
approach
is to
build
the
series
of
constraints
{C[
0
],...,
C[
m
]}
in a
consistent
way.
Parallel
processing
From
a
theoretical point
of
view,
if we
look
at the DSI
algorithm presented
on
page 165,
it is
clear
that
• the
ordering
of the
nodes
of the set /
does
not
matter,
• at
each step
of the
iterative process,
the
application
of the
updating
equation
always
transforms
the
current
function
(p
into
a
function
closer
to the
DSI
solution.
We
conclude
from
these observations
that
the
main loop
of the
iterative algo-
rithm presented
on
page
172 can be
executed
in
parallel
on
several processors
sharing
the
same memory where
the
model
,M
n
(rj,
JV,
</?,£)
is
stored.
181
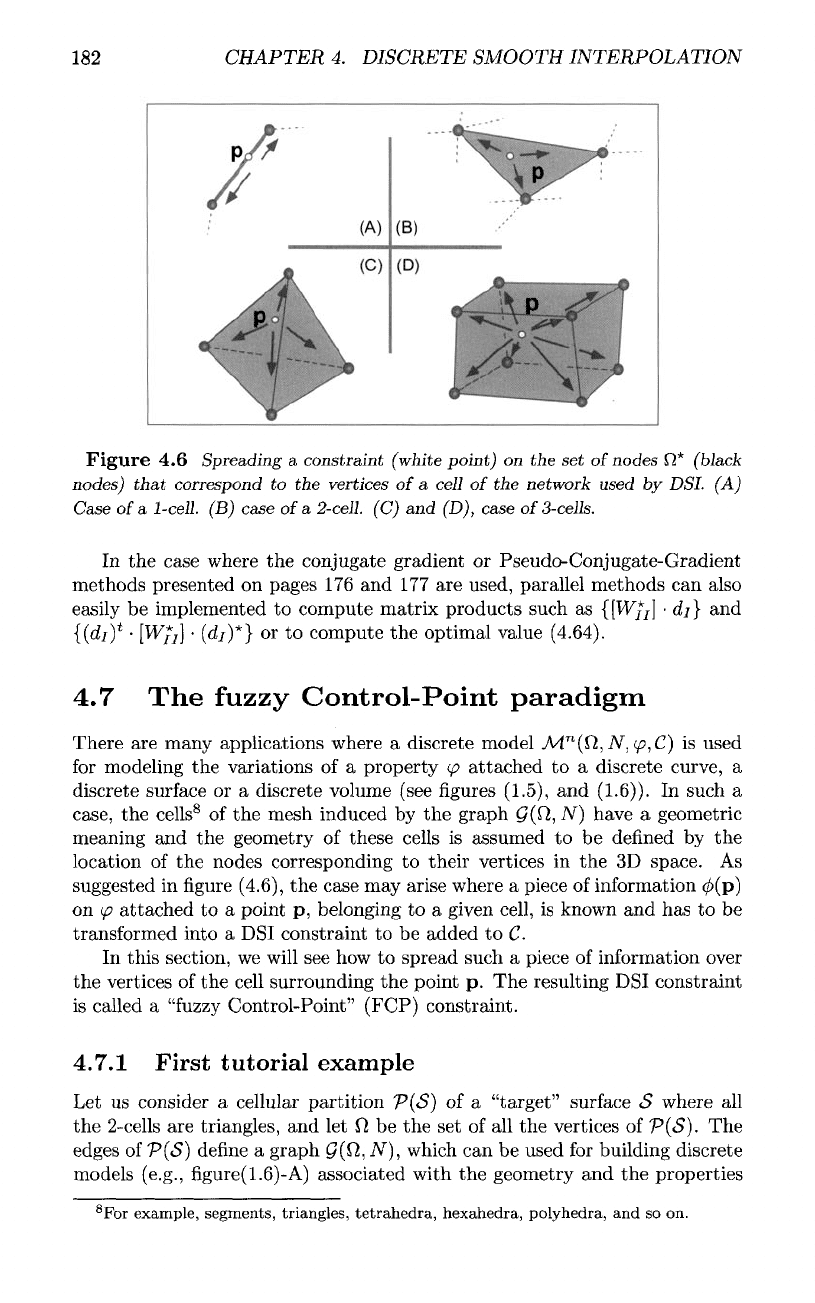
182
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
Figure
4.6
Spreading
a
constraint
(white
point)
on the set
of
nodes
Q*
(black
nodes)
that
correspond
to the
vertices
of a
cell
of the
network
used
by DSL (A)
Case
of a
1-cell.
(B)
case
of a
2-cell.
(C) and
(D), case
of
3-cells.
In
the
case
where
the
conjugate gradient
or
Pseudo-Conjugate-Gradient
methods presented
on
pages
176 and 177 are
used, parallel methods
can
also
easily
be
implemented
to
compute matrix products such
as
{[W/j]
•
dj}
and
{(diY
•
[Wjj]
•
(di}*}
or to
compute
the
optimal value
(4.64).
4.7
The
fuzzy
Control-Point paradigm
There
are
many applications where
a
discrete model
M.
n
(£l,
TV,
95,
C) is
used
for
modeling
the
variations
of a
property
(/?
attached
to a
discrete curve,
a
discrete
surface
or a
discrete volume
(see
figures
(1.5),
and
(1-6)).
In
such
a
case,
the
cells
8
of the
mesh induced
by the
graph
£/(fi,
N)
have
a
geometric
meaning
and the
geometry
of
these cells
is
assumed
to be
defined
by the
location
of the
nodes corresponding
to
their vertices
in the 3D
space.
As
suggested
in figure
(4.6),
the
case
may
arise where
a
piece
of
information
0(p)
on
(p
attached
to a
point
p,
belonging
to a
given cell,
is
known
and has to be
transformed
into
a
DSI
constraint
to be
added
to C.
In
this section,
we
will
see how to
spread such
a
piece
of
information over
the
vertices
of the
cell surrounding
the
point
p. The
resulting
DSI
constraint
is
called
a
"fuzzy
Control-Point" (FCP) constraint.
4.7.1
First tutorial
example
Let us
consider
a
cellular
partition
P(<S]
of a
"target"
surface
<S
where
all
the
2-cells
are
triangles,
and let 0 be the set of all the
vertices
of
P(S}.
The
edges
of
P(S)
define
a
graph
£?(f2,
A/"),
which
can be
used
for
building discrete
models
(e.g.,
figure(1.6)-A)
associated with
the
geometry
and the
properties
8
For
example, segments, triangles,
tetrahedra,
hexahedra, polyhedra,
and so on.

4.7.
THE
FUZZY
CONTROL-POINT
PARADIGM
183
Figure
4.7
Spreading
a
constraint
on the
vertices
of
a
triangle
belonging
to a
triangulated
surface.
of
<5
sampled
at the
vertices
of
P(S}.
For the
sake
of
consistency with further
chapters devoted
to
geometry,
the
location
of any
node
a.
G
1)
will
be
noted
as
x(a)
and the
triangles
of
P(S}
based
on the
vertices
will
be
noted
as !
Fuzzy
Control-Property
Let
Ai
p
(0,
N,
<p,C)
be a
discrete model corresponding
to a
property
9?
of
<S
to be
interpolated over
fi. As
shown
in
figure
(4.7):
• Let p be a
given
point
located
in a
given
triangle
T(x(ao),
X(QI),
x(c*2))
of S
and
corresponding
to the
projection
of a
point
IP on
<S
in a
given
direction
D.
• Let
(Ao(p),
Ai(p),
A2(p)}
be the
barycentric
coordinates
(see
page
254)
of p
relative
to
these three vertices:
be
written
as
The aim is to
define
a
DSI
constraint spread over
the
region
£7*
=
(ao,
ai,
o^)
and
specifying
that
In
other words,
we
would like
to
"project"
the
value
</>(IP)
on the
"target"
<S
in the
direction
D. For
this purpose,
we
propose
to
merge
the
equations
(4.65),
and
(4.66)
into
one
linear
DSI
constraint
c
e
C~,
distributed
on the
region
0*
=
(CKQ,
o^,
Q
2
)
and
defined
by
The linear interpolation

184
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
with:
It is
easy
to
check
that
this
constraint generates
the
following terms
7
c
(cKi)
and
r
c
(oti\(p)
in the
local
form
of the
DSI
equation
at
each node
ctj
G
Q*:
Fuzzy
Control-Point
(sensu
stricto)
Let
us
return
to the
example presented
in the
above section,
and let us
consider
IP as a
"magnet"
attracting
the
point
p of the
triangle
T(X(QO),
x(ai),
x(ai2))
with
a
force
proportional
to a
given factor
w
c
.
In
other words,
we
would like
to
have
p as
close
as
possible
to the
given point
IP
with
a
certainty factor
equal
to
w
c
.
For
this purpose,
the
triangulated surface
S can be
considered
as
being associated with
a
discrete model
A
/
(
3
(0,
.AT,
<£,
C)
where
(p
represents
the
geometry
of S:
In
this
definition
of
</?,
the
values
(X
X
(Q!),X
!/
(Q;),X
;?
(Q;)}
represent
the
coordi-
nates
of the
node
a in the 3D
space,
and we
suggest adapting
the
notion
of
fuzzy
Control-Properties, presented above,
in
such
a way
that
where
(IP
1
,
IP
y
,
IP*}
represent
the
components
of IP in the 3D
space.
In
this
case,
the
"magnet"
IP
attracts
the
point
p and
this generates
a set of
three
independent
"fuzzy
Control-Property" constraints
(c
x
,c
y
,c
z
]
associated with
each
of the
components
of
(p:
This
set of
independent
constraints
is
called
"fuzzy
Control-Point"
and
gen-
erates
the
following
coefficients,
7^(0^)
and
T"(ai\q>),
occurring
in the
local
form
of the DSI
equation
where
Jl*
represents
the set
{aQ,ai,a<2\.
Contrary
to the
notion
of
fuzzy
Control-Property,
in the
case
of a
fuzzy
Control-Point,
the
geometry
is
changing
at
each step
of the
iterative
DSI
algorithm such
that

4.7.
THE
FUZZY CONTROL-POINT PARADIGM
185
• If the
vertices
of
T(X(Q;O),
x(ai),x(a2))
have
moved
in
such
a way
that
p is
still
located
inside
T(x(ao),x(ai),x(a2)),
then
the
barycentric
coordinates
(Ai(p)}
have
to be
updated.
• If the
vertices
of
T(x(ao),
X(QI),
x(a2))
have
moved
in
such
a way
that
p is
now
located
outside
T(x(ao),x(a!i),x(a:2)),
then
we
have
to
look
for a new
triangle
holding
the
projection
p of IP on
S,
and the
barycentric
coordinates
{Ai(p)}
relative
to
this
new
triangle
have
to be
recomputed.
This implies
that
fuzzy
Control-Points have
to be
implemented
as
dynamic
DSI
constraints
(see section
(4.4.4)).
In
practice,
this
type
of
constraint
is
quite
efficient
and
yields excellent results (see [130,
3]).
For
example,
the
modeling
of the
surface presented
in
figure
(1.11)
was
based
on
fuzzy
Control-
Points.
Comment
1:
Generalization
All
of the
above
is
independent
of the
fact
that
the
target
S is a
surface
and
the
fact
that
the
nodes
17*
used
for
spreading
the
constraints
correspond
to
the set of
vertices
of a
triangle.
In
practice, similar results
are
obtained
by
"projecting"
IP at a
point
p
belonging
to a
segment
of a
polygonal curve
(see figure
(4.6)-A),
a
triangle
of a
triangulated
surface (see
figure
(4.6)-B),
a
tetrahedron
of a
tetrahedralized volume (see
figure
(4.6)-C),
a
hexahedron
of
a
volume (see
figure
(4.6)-D),
or any set of
nodes
12*
surrounding
the
impact
point
p.
Comment
2:
Fuzzy
Node-on-Plane
The
notion
of
Node-on-Plane constraint
is the
exact opposite
of the
notion
of
fuzzy
Control-Point (sensu stricto) presented above.
We
would
now
like
to
have
a
node
a to be
attracted
by a
plane
P(p,
N)
passing
by a
point
p
and
orthogonal
to a
unit vector
N. It
should
be
noted
that
the
node
a can
belong
to any
type
of
object,
for
example,
a
curve,
a
surface,
or a
solid.
The
attraction
of a by the
plane
P(p,
N)
tends
to
maintain
the
point
<p(a)
defined
by
equation
(4.68)
in
this plane. This constraint
is
equivalent
to the
following
equation:
This equation
can
easily
be
turned into
the
following
canonic
DSI
constraint
c
=
c(a,
N)
with:

186
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
We
can be
verify
that
this constraint generates
the
following
terms
7^
(a) and
F^(a|(/?)
in the
local
form
of the
DSI
equation
at
node
a:
4.7.2
Second
tutorial
example
Let
us
consider
a
regular
n-grid
as
denned
in
section (3.4),
and let
fi
be the set
of
all the
vertices
of
this grid.
The
edges
of the
grid
define
a
graph
(/(17,
AT),
which
can be
used
for
building discrete models
(e.g.,
see figures
(3.17),
and
(3.18))
where
the
geometry
and the
properties
are
assumed
to be
defined
at
the
vertices
of the
grid.
For the
sake
of
consistency with
further
chapters
devoted
to
geometry,
the
location
of any
node
a 6 0
will
be
noted
as
x(a).
Fuzzy
Control-Property
Let
Ai
p
(fi,
N,
</?,£)
be a
discrete model corresponding
to a
property
(p
to be
interpolated over
the set
O
corresponding
to the
nodes
of the
regular n-grid.
As
shown
in figure
(3.20),
let p =
p(u)
be a
given point
located
in a
given
cell
C,
and let us
assume
that
• the
vertices
{ctii...i
n
'•
ik
G
{0,1}}
of the
cells
are
numbered
as
suggested
in
figure
(3.20),
and
• the
parameter
u
=
[it
1
,..
^u
71
]*
corresponding
to the
location
of p
=
x(u)
in
C is
assumed
to
have
been
determined
according
to the
algorithm
presented
on
page 126.
According
to
equation
(3.16),
an
interpolation
</?c(p)
of
<£
at p =
x(u)
in the
cell
C can be
written
as
with:
As
in the first
tutorial example,
the aim is to
define
a DSI
constraint spread
over
the set of
nodes
0*
consisting
of the
vertices
of C and to
specify
that
where
</>(p)
is a
given value.
For
this
purpose,
we
propose merging equations
(4.70),
and
(4.72) into
one
linear
DSI
constraint
c G
C~,
distributed
on the
region
O*
and
defined
by

4.7.
THE
FUZZY CONTROL-POINT PARADIGM
with:
According
to
equation
(4.49),
such
a
constraint generates
the
following
terms
Jc(&ii...i
n
)
and
r^o^...^!^)
in the
local
form
of the
DSI
equation
at
each
node
ai
l
...i
n
G
0*:
\
Fuzzy
Control-Gradient
In the
same context
as the
fuzzy
Control-Property constraint presented above,
let us now
assume
that
we
want
to
specify
that
where
{<7i(p),
• • •,
<7n(p)}
are
given values while
u =
u(p)
is
determined
as
described
on
page
127.
As can be
seen,
gj(p)
is no
more than
the
jth
(co-
variant) component
of the
gradient
g of the
function
ip
at
location
p
and,
for
this reason,
the set of
n
constraints
(4.74)
is
globally called
a
fuzzy
"Control-
Gradient" constraint.
If
we
define
A^'
in
(p) as
then
equation
(4.70)
implies
that
It can
then
be
deduced
that
the
constraints
(4.74)
are
equivalent
to the
fol-
lowing
DSI
constraints
(c(l,
p),...,
c(n,
p)}
defined
by
187
