Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


168
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
• the
global
roughness
R(tp)
is
smaller
than
R((f>
0
id),
and
• the
smoothed solution
</?
is
close
to
<p
0
id-
By
the
mere installation
of the
following
dynamic constraint, such
a
smooth
solution
can be
very easily obtained using
the
iterative
DSI
algorithm:
This constraint
is a
"fuzzy
Control-Node" constraint similar
to the one
cor-
responding
to
equation (4.52).
The
only
difference
is
that
(p
0
id
is
constantly
modified
to be
equal
to the
value
of
(p
at the
previous iteration.
In the
example shown
in figure
(4.3),
the
efficiency
of the
smoothing
method
is
clearly evident. Here,
the
smoothing algorithm
was
simultane-
ously
applied
to the
components
(<p
x
,
ip
y
,
tp
z
}
of
(/?,
which correspond
to the
location
of the
nodes
of a
surface
in the 3D
space.
Example
2:
Fuzzy
Control-Distance
constraint
Let A be an
object associated with
a
discrete model
.M
3
(fi,./V,
</?,
C)
where
</>
represents
the
geometry
of A:
In
this
definition
of
</?,
the
values
{x
x
(a),x
?/
(Q:),x
2:
(Q:)}
represent
the
coor-
dinates
of the
node
a in the 3D
space.
As
suggested
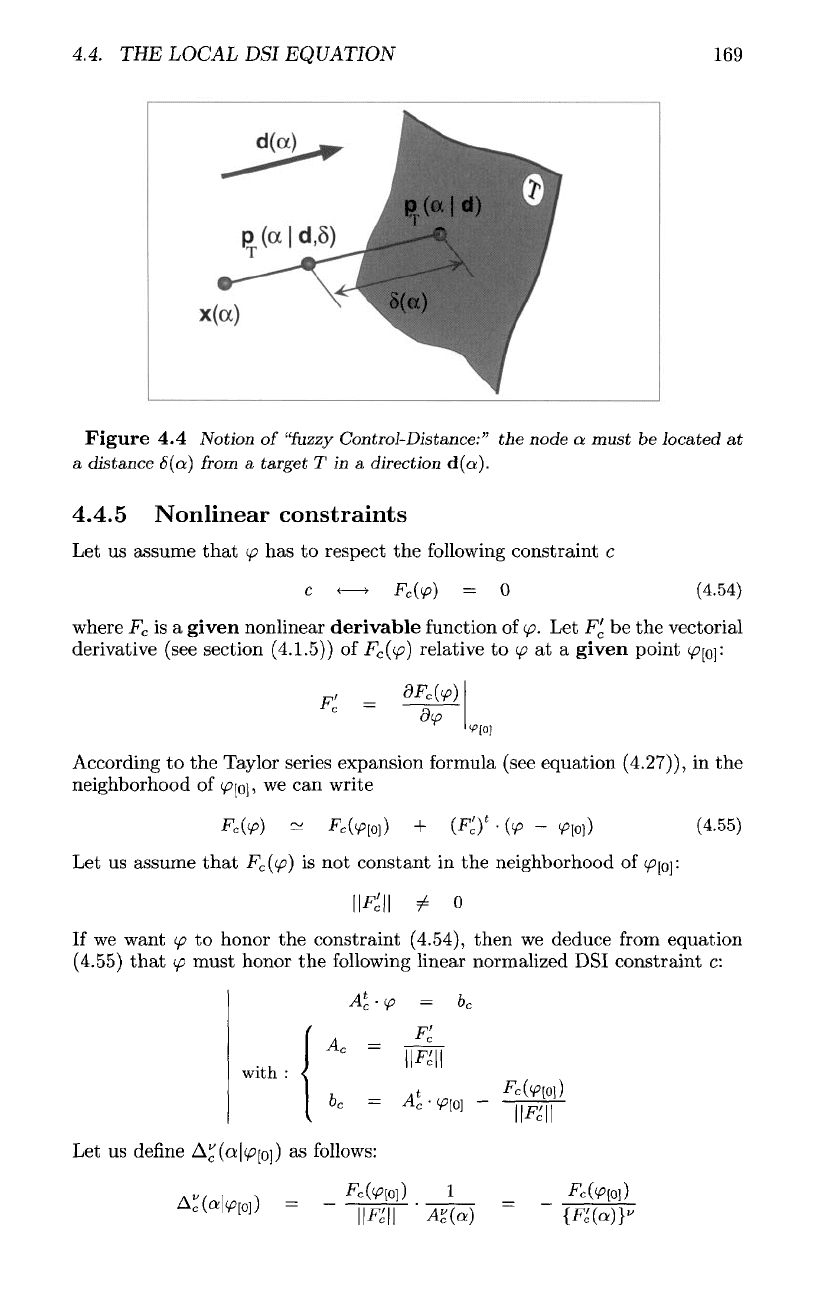
in figure
(4.4),
let us
consider
a
situation where
•
d(a)
is a
given
direction
attached
to a, and
•
p
r
(a|d)
is the
impact point
on a
target
T of the
straight line
launched
from
a in the
direction
d(a).
By
definition,
we
call
a
"fuzzy
Control-Distance" constraint
a DSI
constraint
specifying
that
a
must
be
located
at a
given distance
6(a)
from
T in the
direction
d(a).
If
we
note
p
T
(a|d,
8} as the
point
such
that
then
it is
easy
to see
that
the
notion
of
"fuzzy
Control-Distance"
can be
implemented
as a
"fuzzy
Control-Node" (see page 164) such
that
It
should
be
noted
that
x(a)
moves
at
each iteration
of the DSI
method
and
the
impact point
p
T
(a|d)
has to be
updated
at
each iteration. This clearly
shows
that
the
"fuzzy
Control-Distance" constraint
so
defined
is a
dynamic
constraint.
4.4.
THE
LOCAL
DSIEQ
UATION
169
Figure
4.4
Notion
of
"fuzzy
Control-Distance:"
the
node
a
must
be
located
at
a
distance
6(a)
from
a
target
T in a
direction
d(a).
4.4.5
Nonlinear constraints
Let us
assume
that
(p
has to
respect
the following
constraint
c
where
F
c
is a
given
nonlinear
derivable
function
of
(p.
Let
F'
c
be the
vectorial
derivative
(see section
(4.1.5))
of
F
c
((p)
relative
to
9?
at a
given
point
(p^y.
According
to the
Taylor series expansion
formula
(see equation
(4.27)),
in the
neighborhood of </?[o] > we can write
Let us
assume
that
F
c
((p)
is not
constant
in the
neighborhood
of
<p^:
If
we
want
(p
to
honor
the
constraint
(4.54),
then
we
deduce
from
equation
(4.55)
that
(p
must honor
the
following linear normalized
DSI
constraint
c:
Let us
define
A£(a|</>[o])
as
follows:

170
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
According
to
equations
(4.49),
and
(4.51),
we
conclude
that
the
terms
7e
(a)
and
r^(a|c/?)
associated with
the
above constraint
are
such
that
4.5
Accounting
for
hard constraints
Definitions
Let us
assume
that
the
solution
(p
of our
problem
has to
honor strictly
the
sets
C
=
and
C-
5
"
corresponding
to
hard constraints
as
defined
by
equations (1.5),
and
(1.6). Using
the
notations
introduced
on
page
140,
these
constraints
can
be
written
as
follows:
For any
point
(p
in
JR
n
'
M
,
the
notions
of
active
and
inactive
constraints
are
defined
as follows:
It
should
be
noted
that
the
resulting constraint
is a
"dynamic"
DSI
constraint
because
the
coefficients
A
v
c
(a) and
b
c
have
to be
updated
at
each
step
of the
iterative process.
As a
consequence,
we are not
sure
of the
uniqueness
of the
solution yielded
by the DSI
iterative algorithm. Theoretically,
the
solution
so
obtained
may
depend
on the
initial
solution
ip^.
Remark
The
term
A^(a|(/?[
0
])
m
the
equation
(4.56)
can be
interpreted
as a
"repelling
force"
that
tends
to
pull
<f>
v
(ot)
away
from
its
current value
(ip
v
(a)}^.
As a
consequence,
the
local
DSI
equation
(4.46)
will
tend
to
transform
(p
v
(ot)
in
such
a way
that
From
a
practical
point
of
view, dynamic
constraints
work
fine
only
if the
mod-
ifications
of the
constraints between
two
successive iterations have
a
relatively
small amplitude.
This
suggests
that
we
replace
the
term
Ap(a|<^[
0
])
i
n
the
equation
(4.56)
by the
term
A^(a|(/?[
0
])
defined
as follows:
In the
above expression,
the
chosen value
of
e
should
be
small enough
to
prevent large modifications
of
^p
v
(a) at
each iteration.

4.5.
ACCOUNTING
FOR
HARD
CONSTRAINTS
Withi n
the
framework
of
optimization theory
[90],
such notions
of
active
and
inactive
constraints
are
used
to
introduce
the
following
concepts:
• A
constraint
c
e
C
=
or c
£
C>
is
said
to be
honored
if it is
inactive.
•
<p
is
said
to be a
feasible
point
if, and
only
if, all the
constraints
are
inactive
at
that
point.
• The set of all the
feasible points
<p
is
called
a
feasible
region.
• The set
A(C~,
C
>
\<p]
of all the
active hard constraints
at
point
ip
is
called
the
active
set at
(p.
Active
set
method
Let
us
assume
that
an
approximated solution corresponding
to a
feasible
point
V?[
0
]
is
known
and
that
the aim is to
find,
in the
neighborhood
of
</?[
0
],
a new
point
corresponding
to a
lower
value
of the
global roughness
R*((p~).
For
this
purpose,
we
propose
to
proceed iteratively
for
each node
a of the
graph
as
follows:
1.
Let
(p
be a new
point
of
JR
n
'
M
deduced
from
</?[Q]
by
replacing
the
components
{</7[o](«)}
by the
values
obtained
with
the
local
DSI
equation
(4.46) without
taking
any
hard constraints into account.
2.
Build
the set
A.(C~,
C
5
*)^)
of
active constraints
at
point
(p.
3.
Look
for a
point
tp*
such
that
Determining
(p*
Let
H
c be the hyperplane of lRn associated with a hard constraint c E C
(see
page 141). Complying with item
3 of the
active
set
method introduced
above
implies
finding
that
point
of
H
c
that
is the
closest
to the
current point
(p.
In
other words,
(p
must
be
equal
to the
orthogonal projection
of
(p
on
H
c
.
Bearing
in
mind
the
fact
that
A
c
is
orthogonal
to
H
c
,
it is
easy
to
check
that
the
orthogonal projection
(p*
of
(p
on
H
c
is
defined
by
(see
figure
(4.1)):
171

172
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
Throughout this chapter,
it has
been assumed
that
the
constraints
are
nor-
malized
(see page 140), which, according
to
equation
(4.4),
implies
that
the
above
formula
can be
written
in the
following
simpler way:
Iterative
algorithm
To
account
for
hard constraints,
we
suggest slightly
modifying
the
iterative
version
of the
DSI
algorithm based
on the
local
DSI
equation:
//—
DSI
algorithm
with dynamic
and
hard
constraints
let I be the set of
nodes
where
</?(a)
is
unknown
let
(f>
=
y>[o]
be a
given initial approximated solution
let
w
be an
estimated
value
of the
balancing
factor
while
(
more
iterations
are
needed
) {
for_all(
a
e
/ ) {
for_all(
v
}
{
}
while(
A(C
=
,
C**
\i{>)
is not
empty
) {
•
choose
a
constraint
•
compute
•
update
•
update
}
for_all(
c
<E
C ) {
if(
c is
dynamic
) •
update
c
}
}
Jl
end :
for_all(
a € I )
} // end :
while
(
more
iterations
are
needed
)
Existence
and
uniqueness
of the
solution
Let R™' be the subspace of ]Rn corresponding to the components of <^/.
Eac h hyperplane
H
c
corresponding
to a
hard constraint
c
intersects
IR™'
according
to a
"hyper-straight-line"
H*:
As
suggested
in figure
(4.5),
the set of all
these
hyperstraight-lines
is
bounding
a
region
H of
IR^
M
defined
by
4.5.
ACCOUNTING
FOR
HARD CONSTRAINTS
173
Figure
4.5
Minimizing
the
global roughness
(represented
by
contour lines)
in
the
feasible
domain
H.
denned
by
hard constraints
(dashed
area):
initial
and final
solutions
are
represented
by
white
and
black circles, respectively. Parts
(A) and (C)
show
the
cases
of
one and two
equality constraints, respectively, while part
(B)
shows
the
case
of
an
inequality constraint
and
part
(D) a
combination
of
an
inequality
and
an
equality constraint.
It is
clear
that
H.
is a
convex
subset
of
M™'
,
and,
provided
that
7i
is not
empty, this implies that any convex function denned on JR™ has only one
minimum
in
Ji.
If we
observe
that
any
positive
definite
quadratic
function
such
as, for
example,
the
global
roughness
R*(y>),
is
convex,
then
we can
conclude
that
if : the set of
hard constraints
is not
empty
and
there
is at
least
one
feasible point
then
: the
DSI
solution exists
and is
unique
Convergence
If
the set
H
of
feasible
solutions
is not
empty,
then
convergence
of the
iterative
algorithm
presented
on
page
172 is
ensured
by the
fact
that
the
generalized
global
roughness
R*(<p)
decreases
at
each
step
of the
main
loop.
To
understand
the way
this
algorithm
leads
the
current
value
of
(f>
toward
the DSI
solution,
let us
refer
to the
examples
shown
in figure
(4.5)
where:
• the
contour lines correspond
to the
mapping
of the
variations
of the
global
roughness
R*(y>}
in the
subspace
JR?'
M
,

174
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
• the
initial
solution
c^
'
is
represented
by a
white
circle, while
the
DSI
solution
is
represented
by a
black circle,
and
• the
feasible region
Ti.
corresponds
to one of the
following:
1.
one
hyperplane
H
c
associated with
one
equality constraint
(see
figure
(4.5)-A),
2.
a
convex region bounded
by a
series
of
hyperplanes
{H
c
}
associated
with
inequality
constraints
(see
figure
(4.5)-B),
3.
a
mixing
of the
cases
(1) and (2)
where
the
hyperplane
H
c
associated
with
an
equality constraint
is
"clipped"
to a
convex region
associated
with
a set of
equality
constraints
(see
figure
(4.5)-D),
or
4.
the
intersection
of two (or
more) hyperplanes
H
c
corresponding
to
equal-
ity
constraints
(see
figure
(4.5)-C).
As
can be
seen
in
figure
(4.5),
the
updating formula
tends
to
pull
the
current solution
<£>
toward
the
minimum
of
R*(^}
while
the
loop
while(
A(C~,C
>
\ip)
is not
empty
) {
•
choose
a
constraint
•
update
•
update
}
systematically
projects this current solution orthogonally
on the
convex
do-
main
7i.
4.6
Accelerating
the
convergence
The DSI
problem
is no
more
than
a
particular
quadratic
programming prob-
lem
and the
local
DSI
equation
can be
viewed
as the
well-known steepest
descent method. This suggests
that
traditional methods dedicated
to
this
kind
of
problem
(e.g.,
[141,
90])
can be
used
for
accelerating
the
convergence
of
the
iterative
DSI
algorithm
as, for
example:
• the
successive over-relaxation method (e.g.,
[209],
[177]),
and
• the
conjugate gradient method (e.g.,
[209],
[90],
[177]).
Each
of
these methods
is
based
on the
same principle, which consists
of
using
the
result
of
iteration
[p—
1] to
improve
the
result
of
iteration
\p\.
The first one
corresponds
to a
local strategy, while
the
second involves
a
global approach.

4.6.
ACCELERATING
THE
CONVERGENCE
175
4.6.1
Traditional
methods
Successive
Over-Relaxation
This method relies
on the
following
implicit assumption:
If
the
convergence
is
monotonic,
then
it is
possible
to use the
"direction"
of
variation
of(p
for
updating
(p
by a new
value beyond
the
"optimal" value proposed
by the
local
DSI
equation.
In
other words,
if
<p^
ld
(a)
is the
value obtained
at
iteration
\p—
1] and
^
ew
(a)
the
"optimal"
new
value yielded
by
equation
(4.46),
then
(p
v
(oi)
should
be
updated according
to the
following
schema:
This updating equation
is
generally written
in the
following
equivalent way:
The
factor
LJ
is the
so-called "over-relaxation"
coefficient,
which
is in
general
taken
to be in the
range
[1,2].
The
optimum choice
of
a;
depends
on all
the
parameters
of the
discrete model
A4
n
(f2,
TV,
<f>,C}.
Rather
than
trying
to
determine
this
optimal value
of
a;,
it is
simpler
to use an
average value
determined experimentally.
In
practice,
in the
case
of
DSI,
the
value
uj
= 1.5
seems generally
to
yield excellent
results
([46,
50]).
From
the
programming
point
of
view,
the
implementation
of
this method
has
little impact
on the DSI
iterative
algorithm:
//—
DSI
algorithm with over-relaxation
let
/
be the set of
nodes
where
(p(oi)
is
unknown
let
<£>
=
y>[o]
be a
given
initial
approximated
solution
let
w
be an
estimated
value
of the
balancing
factor
while(
more
iterations
are
needed
) {
for_all(
a € / ) {
for_all(
v ) {
} // end :
for_all(
a
e
/ )
} // end :
while(
more
iterations
are
needed

176
CHAPTER
4.
DISCRETE SMOOTH INTERPOLATION
The
Conjugate-Gradient
method
Let
us
assume
that
there
are
neither dynamic
nor
hard constraints except
those corresponding
to
C
L
.
In
this case, according
to
equation
(4.32),
the
solution
(pi
of the DSI
problem corresponds
to the
minimum
of the
quadratic
form
R*(<p)
or,
equivalently,
to the
minimum
of
(^
•
JR*(</?))
defined
by
Let
]R™'
M
be the
subspace
of
M
n
'
M
corresponding
to the (n •
|/|) unknown
components
of
</?
stored
in the
submatrix
<£>/,
and let
Rj(ipi)
be the
restriction
of
R*(<p)
considered
as a
function
of
</?/
only. According
to
equation
(4.33),
the
gradient
gradi
of
(|
•
R$((pj})
relatively
to
</?/
is
such
that
The
idea
of the
conjugate gradient method
is to
build progressively
at
each
iteration,
a
series
of
independent directions
{d/[
0
]
5
d/[i],...,
d/[p]}
of
JR™'
M
and
to
determine
a
step
(scalar value)
s\
p
]
in the
direction
d^
such
that
It can be
shown
(e.g.,
see
[90])
that
the
optimal step
S[
P
]
in the
direction
d/[
p
]
is
such
that
At
each iteration
p,
the
direction
d/[
p
]
is
obtained
as a
linear combination
of
the
gradient
gradj^
at
point
y>/[
p
],
with directions
{^/[o],<^/[i],
• • •
,^/[
p
-i]}
obtained
at
previous iterations.
The
coefficients
of
this linear combination
are
chosen
in
such
a way
that
rf/[
p
] is
"conjugate" relative
to all the
previous
directions
in the
following
sense:
As
a
consequence
of
this
"conjugacy"
property,
it is
possible
to
show
(e.g.,
see
[90,
163])
that
the
gradient
gradi^
p+
^
at
iteration
\p
+
I]
and the
associated
direction
d/[
p
+i]
can
simply
be
updated according
to the
following
equations:
The
conjugate gradient method
can
then
be
implemented according
to the
following
iterative algorithm:
//—
DSI
algorithm
using
Conjugate-Gradient
let
/
be the set of
nodes
where
ip(a)
is
unknown
let
(p
*—
<£>[o]
be a
given
initial
approximated
solution

let
gradi
<—
[Wjj]
•
<pr
~
ipi
let
di
<—
—
gradi
and 7
<—
||gra<i/||
2
while(
more
iterations
are
needed
) {
•
compute
the
optimal value
s
}
If
end :
while(
more iterations
are
needed
)
This method
is
very
efficient.
Furthermore,
it is
possible
to
prove
that
it
converges
in, at
most,
(n •
|/|)
iterations.
However,
there
are two
major
drawbacks:
1.
Because
ipj
is
used only
in the
initialization phase,
it is
impossible
to
change
if)i
between
two
iterations,
implying
that
dynamic
constraints
cannot
be
taken
into account.
2.
The
method
does
not
allow
hard
equality
or
inequality
constraints
to be
taken
into account.
For
these reasons,
the
next section proposes
a
"pseudo"
Conjugate-Gradient
method
that also converges very rapidly,
yet
still
offers
the
possibility
of
taking
hard
and
dynamic constraints into account.
The
Pseudo-Conjugate-Gradient method
Taking
into account equation
(4.45),
we can
observe that,
for all a
e
O
and
all
v
6
{!,...,n},
the
components
{gradf(a)}
of the
vector gradi
in the
conjugate
gradient method presented above
are
such
that
This suggests
modifying
the
conjugate gradient algorithm
as
follows:
//—
DSI
algorithm using Pseudo-Conjugate-Gradient
let / be the set of
nodes where
<p(a)
is
unknown
let
ip
<—
c/?[o]
be a
given initial approximated solution
let
gradi
be the
vector
defined
by
equation (4.59)
let
di
<—
—gradi
and 7
<—
||grad/||
2
while(
more iterations
are
needed
) {
•
determine
the
optimal value
s
such
that
while(
A(C
=
,C
>
\(p)
is not
empty
) {
4.6.
ACCELERATING THE CONVERGENCE
177
