James I.N. Introduction to Circulating Atmospheres
Подождите немного. Документ загружается.


2.6 Problems
59
The SGCM makes
no
attempt
to
simulate
the
stratosphere.
In the
GCM,
the temperature field,
and
hence,
by
thermal wind balance,
the
zonal wind
field in
the
lower stratosphere,
are
sensitive
to the
details
of the
radiation
scheme and the deep convection scheme. But
it
is clear from the diagram that
the SGCM captures many
of
the basic processes which determine
the
gross
features
of the
zonal wind field. Later,
we
shall
see
that
it
also simulates
various eddy fluxes
of
heat
and
momentum surprisingly realistically.
2.6 Problems
2.1 Show that
Q
f
R
(
=
QR-QR.
2.2
If
Q
is
some conserved quantity such that DQ/Dt
=
0, and Q
is
inde-
pendent
of
height, show that the root mean square meridional displacement
of air parcels
is
Qy
2.3 Show that
a
finite difference analogue
of
the second derivative can
be
written:
^
=
g
+1
-2g
+
e:,
1+ 2
dx
2
Ax
2
Using this formula and centred time differencing, show that the finite differ-
ence analogue
of
the linear diffusion equation:
dt
dx
2
is numerically unstable
for all At.
Suggest
a
modification
of
this finite
difference representation which would
be
stable.
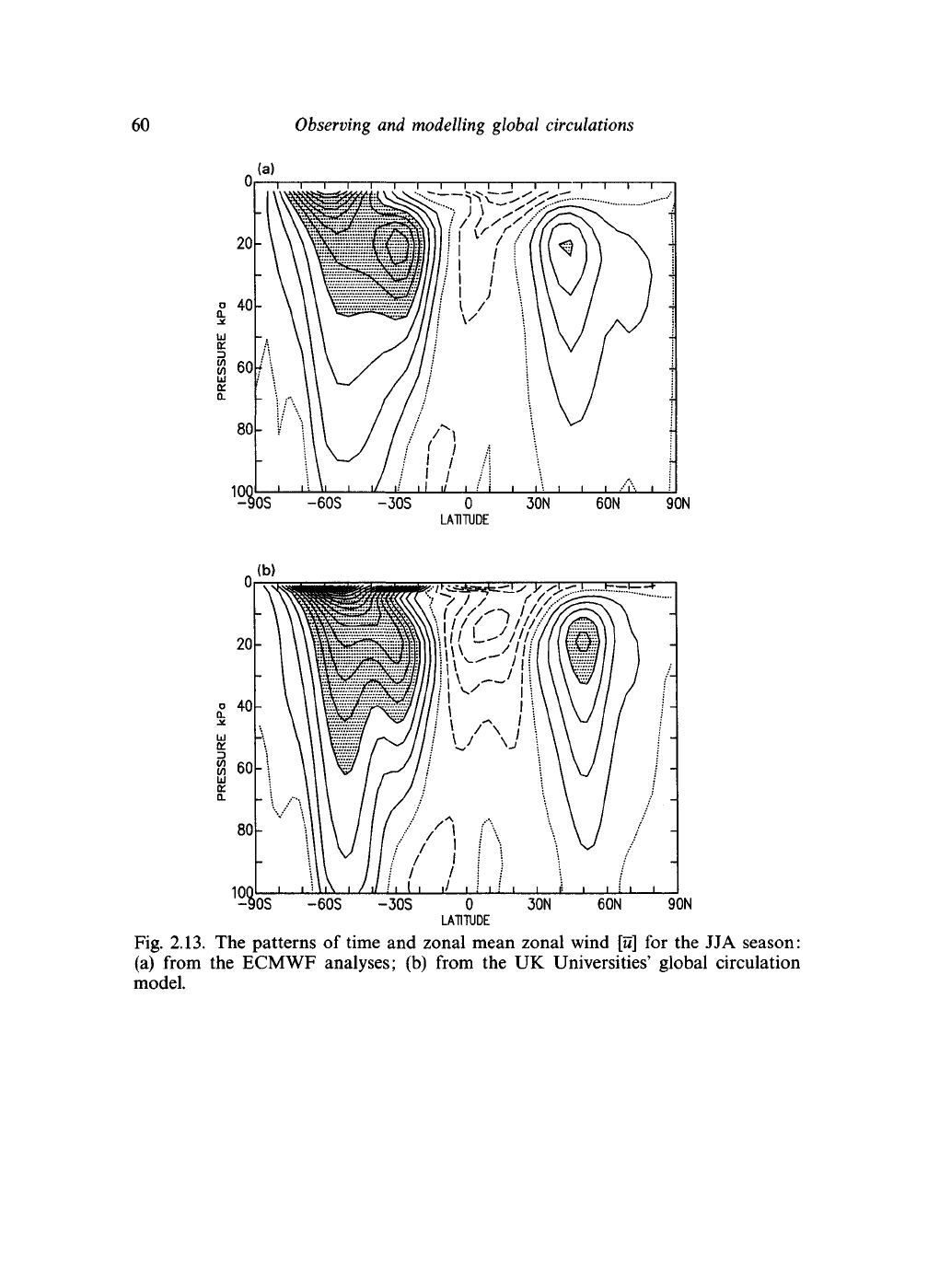
60
Observing and modelling global circulations
0
LATITUDE
i r- i i ; i i
-60S
-30S 0 30N 60N 90N
LATITUDE
Fig. 2.13. The patterns of time and zonal mean zonal wind
[u]
for the JJA season:
(a) from the ECMWF analyses; (b) from the UK Universities' global circulation
model.
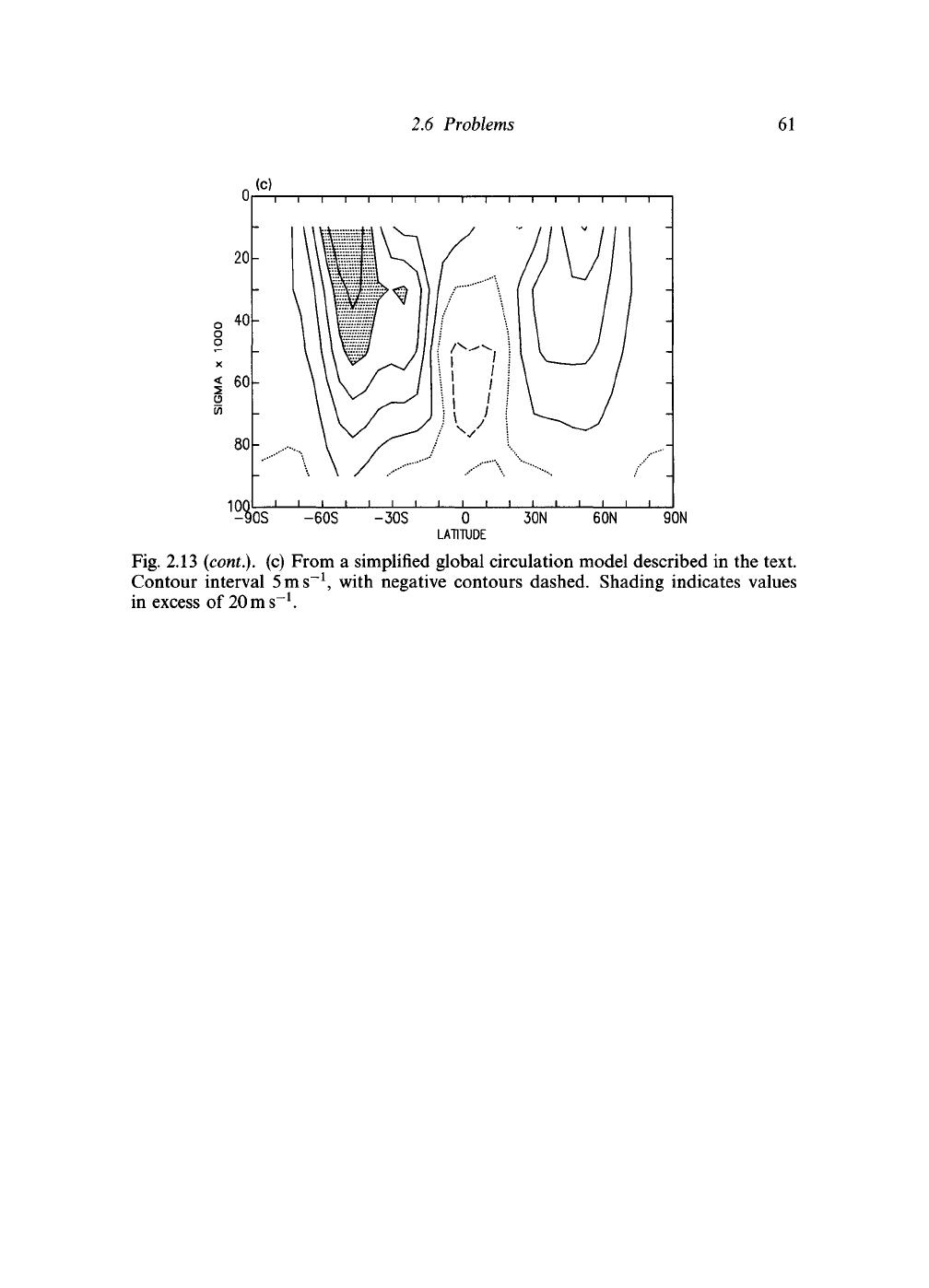
2.6 Problems
61
0
LATITUDE
Fig. 2.13
(cont.).
(c) From a simplified global circulation model described in the text.
Contour interval
5
ms"
1
, with negative contours dashed. Shading indicates values
in excess of
20
ms"
1
.

3
The atmospheric heat engine
3.1 Global energy balance
In this section, we will discuss some basic principles which will help to
describe the thermal forcing of the global circulation. For the present, we
consider the global mean energy balance of the atmosphere; in the next
section we will consider the geographical variations of this balance. In these
sections, we wish to introduce the concept of radiative equilibrium, and
to indicate how a timescale for establishing such an equilibrium might be
estimated.
The basic physical principle to be used is Stefan's law. This states that the
radiant energy emitted per unit area of a perfectly black body is proportional
to the fourth power of its temperature:
S =
GT\ (3.1)
where a is the Stefan-Boltzman constant and has the value 5.67 x
10~
8
Wm~
2
K~
4
. For our purposes, it will be adequate to regard a slab of
gas,
the surface of the Earth or the surface of the sun as black bodies which
obey Stefan's law.
A black body emits radiation with a range of frequencies, but with a
maximum at frequency v
max
. Wien's displacement law relates v
max
to the
temperature of the black body:
Vmax = WT, (3.2)
where W is a constant which has the value 1.035 x 10
11
K"
1
s"
1
. Figure 3.1
shows graphs of energy versus frequency for black bodies at different tem-
peratures. The Sun, with a surface temperature of around 5750 K, radiates
mainly at visible and near infrared wavelengths, with a maximum in the
visible part of the spectrum. The clear atmosphere is nearly transparent to
62

3.1 Global energy balance
63
5750K
1111
1—i—f—i—i
i 111
1—i—i—i
i 1111
10"
4
10"
3
10"
Wavelength (cm)
Fig. 3.1. Curves showing the radiation emitted per unit frequency as a function of
frequency for black bodies with temperatures of 255 K and 5750 K.
these wavelengths, so most sunlight will reach the ground, or at least the tro-
pospheric levels where the cloud tops are situated. In fact, most gases which
form planetary atmospheres transmit sunlight with little absorption. The
atmosphere
itself,
with typical temperatures of 200-300 K, radiates at much
longer wavelengths, in the infrared part of the spectrum. The atmosphere
is rather opaque at these wavelengths. Trace constituents such as water
vapour, carbon dioxide and (at stratospheric levels) ozone, provide most
of this absorption. Thus the surface is unable to radiate directly to space,
and receives additional long wave radiation from the overlying layers of the
atmosphere. Its temperature is raised above the equilibrium expected for an
airless body. The atmosphere behaves rather like a blanket, trapping heat
near the surface and raising its temperature, an effect popularly mis-named
the 'greenhouse' effect.
These concepts can be made quantitative. Let the solar radiation flux
incident upon the Earth be S; S is sometimes called the 'solar constant',
though in fact it varies through the year as the Earth-Sun distance fluctuates.
The mean value of S is
1370
Wm~
2
.
The Earth presents an area na
2
normal
to the solar beam but has a total surface area of
Ana
2
;
the mean flux of solar

64
The atmospheric heat engine
Net Solar
Radiation
(l-a)S/4
(l-a)S/4
Ground
Radiation
I"-
Atmosphere
Temperature
T
U
Atmospheric
Radiation
e)U
T B
T
a
Ground, temperature
T
g
Fig. 3.2. Single slab model
of
the Earth-atmosphere system.
radiation
per
unit area
of
the Earth's surface
is
therefore
S/4.
A
fraction
a
of the incident sunlight
is
simply reflected straight back
to
space;
a is
the
'albedo'
and
is
0.29
for
the
Earth, though there
are
strong
and
important
local variations.
The
albedo
of
cloud
or
fresh snow
is
large,
as
much
as
0.90, while that
of
forest
or
ocean surface
is
less than 0.07.
A
total flux
/
=
(1
— cc)S/4
is
absorbed
by the
Earth;
in the
steady state this must
balance
the
infrared radiation emitted
by
the
Earth. Using
Eq.
(3.1),
the
mean temperature
of
the Earth-atmosphere system
is
therefore:
-{••
-«)sy
4(7
J
(3.3)
The temperature defined
in
this way
is
sometimes called
the
'bolometric'
or
'brightness' temperature;
it is
the
temperature which
a
black body would
have
to
have
in
order
to
radiate
the
same flux
of
infrared radiation. Substi-
tuting values
for the
Earth leads
to T
B
=
255
K. This
is
considerably colder
than
the
mean temperature
of
the Earth's surface (which
is
close
to
288
K).
The bolometric temperature
T
B
may
be
thought
of
as
a
temperature typical
of the higher layers
of
the troposphere which
can
radiate infrared radiation
directly
to
space. The surface
and
the lower layers
of
the atmosphere can
be
much warmer, provided
the
atmosphere
is
opaque
to
infrared radiation.
This
may
be
demonstrated
if
the
atmosphere
is
regarded
as a
single
uniform slab
of
gas lying above the Earth's surface,
as
shown
in
Fig. 3.2.
For
simplicity, assume that
the
atmosphere
is
completely transparent
to
visible
radiation,
but
that
it
absorbs
a
fraction
6 of
the
infrared radiation which

3.1
Global energy balance
65
impinges upon it. The ground emits radiant energy at a rate U, of which a
fraction (1
—
e) escapes to space, while the warm atmosphere emits B both
into the ground and to space. The temperature of the ground T
g
and of the
air T
a
are obtained from Eq. (3.1):
g
l
'\ (3.4)
In the steady state, the fluxes into and out of the ground must balance:
(l-a)|
+ B = l/, (3.5)
as must the fluxes into and out of the atmosphere:
IB = eU. (3.6)
Eliminating B between these equations and using Eq. (3.3), we find
r
* = \2=7}
T
*
(3
-
7)
and similarly
Thus,
in the limit of an atmosphere totally opaque to infrared radiation, i.e.,
e
—>
1, we have that T
g
= 2
1
/
4
T
B
and T
a
= T
B
; the surface is warmer than
the overlying atmosphere. Taking T
B
as 255 K gives T
g
= 303 K, somewhat
warmer than observed. Using a more modest value of e = 0.771 gives the
observed T
g
of 288 K. In this case, T
a
= 227 K, suggesting that a more
transparent atmosphere would have an even stronger lapse rate in radiative
equilibrium. A more sophisticated calculation, using a multilevel approxima-
tion to the vertical structure of the atmosphere would yield a higher surface
temperature; such a model is needed to account for the extremely high
surface temperatures of Venus. It could include additional processes such
as scattering of radiation by aerosols. The action of radiation alone would
eventually establish an equilibrium temperature structure, with temperature
decreasing with height and depending upon the intensity of the incoming
solar radiation. This equilibrium is called 'radiative equilibrium'.
Now consider the time taken to establish such a radiative equilibrium
temperature. This can be estimated as follows. Suppose that by some
unspecified agency the atmospheric temperature is disturbed away from
radiative equilibrium. For simplicity, suppose that the surface has negligible
thermal capacity; in that case, Eq. (3.5) still holds. But Eq. (3.6) must be

66
The
atmospheric
heat
engine
rewritten
C
J*i^=eU-2B,
(3.9)
g
At
where p
s
is the surface pressure; c
p
p
s
/g is the thermal capacity of an
atmospheric column of unit cross sectional area. Write T
a
=
T
a
o+AT,
where
T
a
o is the equilibrium value calculated from Eq. (3.7), and | AT |<C
T
a
o.
Then
Eq. (3.9) can be linearized about T
a
o'.
d
=
_4(2
f
)aTi
)gAT
d£
p
s
c
p
This
equation has a simple and well-known solution: AT decays exponen-
tially
on a timescale T
E
where
which is called the 'radiative equilibrium timescale'. If the radiative timescale
is long compared to the typical timescale for motions in the atmosphere, then
fluid motions can maintain the atmospheric temperature far from radiative
equilibrium; on the other hand, if
T
E
is short, meteorology will do little to
disturb radiative equilibrium. For the Earth, we suppose that e is 1 so that
T
B
is
255
K; then
T
E
from Eq. (3.11) is around 30 days. This is much longer
than the typical timescales of 1-5 days associated with advection by large
scale tropospheric weather systems, and so we anticipate that the circulation
of the atmosphere will greatly modify its thermal structure.
The kind of model which has been described in this section is some-
times called an 'energy balance' climate model. Such models use the global
mean incoming and outgoing fluxes of energy to estimate the global mean
temperatures. More sophisticated versions of the genre include complicated
feedback effects, such as ice-albedo feedbacks. Of course, they give no
guidance as to global circulation, which is driven by variations of the tem-
perature fields from place to place in the atmosphere. Indeed, because of
the complicated nonlinearities within the climate system, such simple energy
balance models do not even give a very reliable guide to the global mean
climate, though they have been used to yield interesting possibilities about
the sensitivity of climate to various kinds of perturbation.
3.2 Local radiative balance
The arguments of the preceding section were global. But the large scale
circulation of the atmosphere is driven by variations of temperature from

3.2
Local radiative balance
67
place to place. So in this section, the geographical variations of the radiation
field will be described. These geographical variations will also change with
time,
thus inducing diurnal and seasonal changes into the atmospheric
circulation.
Both the incoming solar radiation and the albedo of the Earth vary
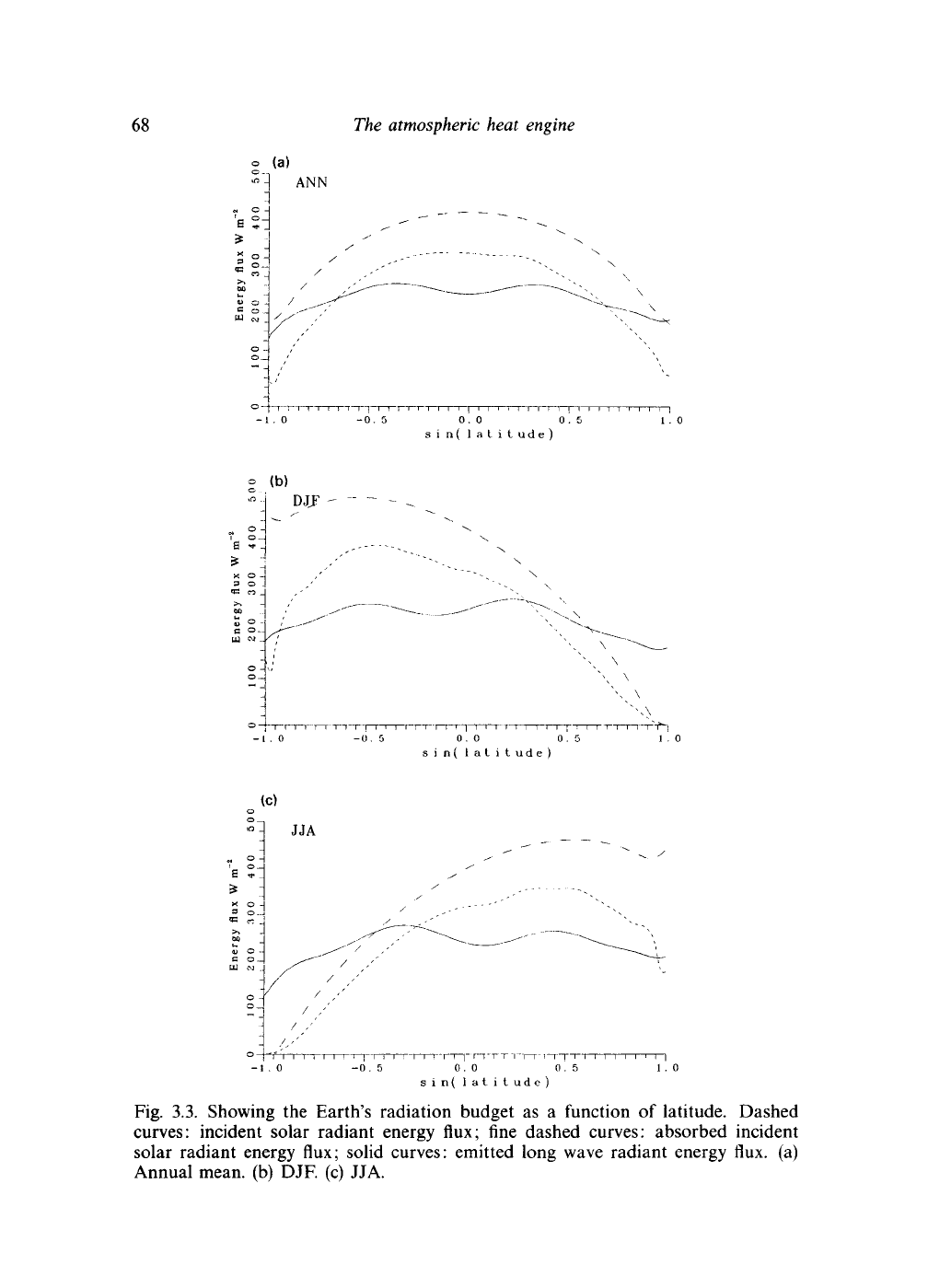
strongly with latitude. Figure 3.3(a) shows the annual mean incoming solar
radiant energy flux plotted against latitude. We denote this incoming flux
of radiation /. The global mean value of / is of course S/4, as shown
in the last section. Geometrical factors mean that / is large in the tropics
but considerably smaller at the poles. Were it not for the axial tilt of the
Earth, the polar value would of course be zero. As it is, there is substantial
insolation at the poles in the summer. In fact, the local value of / is a
maximum at the pole, for a time around the summer solstice. The equator
to pole decline of the annual mean / is accentuated by the variations of
albedo. The albedo of high latitudes, where the snow and ice cover is
large and permanent, is much higher than at lower latitudes. Again, the
midlatitudes are more cloudy than the subtropics. As a result, a nearly
constant short wave flux of about
100
Wm~
2
is reflected directly back to
space at all latitudes. Thus the radiation absorbed by the Earth and its
atmosphere varies from around
100
Wm~
2
at the poles to near
400
Wm~
2
at the equator.
The local radiative equilibrium temperature can be calculated in the same
way as can the global radiative equilibrium temperature, using Stefan's law.
The local bolometric temperature is given by:
T
B
=
(SJo)
l
'\
(3.12)
where S
L
denotes the local absorbed solar radiation. At the pole, the annual
mean value of T
B
would be around 205 K from this formula, while at the
equator we find 290 K. Using Eq. (3.7) to estimate a surface temperature,
assuming e =
0.771,
the equator-pole temperature difference would be about
96
K.
In fact, this temperature difference is much larger than observed. The
annual average temperature difference is around 35 K, with the poles con-
siderably warmer than would be predicted from local radiative balance, and
the tropics rather cooler. The third curve in Fig. 3.3(a) shows the outgoing
long wave radiation plotted against latitude. It is a considerably flatter curve
than that for S
L
, reflecting that the temperature contrast is smaller than it
would be in radiative equilibrium. Of course, the total outgoing radiation,
integrated over the globe balances the total incoming radiation. But locally,
the imbalances are substantial. These local imbalances are a manifestation
68
The atmospheric heat engine
(a)
ANN
1
o
—(-—
r
-
->—
r
—
-1.0
-0.5
0.0 0.
si n( latitude)
(b)
DJF -
1*1
(0
JJA
°
H
i
;
1
-0.5 0.0
sin( latitude)
\ \
i—i—r~i—i—|~T~7"T'T"
-\—\—r""i~
0.0
sin(latitude)
Fig. 3.3. Showing the Earth's radiation budget as a function of latitude. Dashed
curves: incident solar radiant energy flux; fine dashed curves: absorbed incident
solar radiant energy flux; solid curves: emitted long wave radiant energy flux, (a)
Annual mean, (b) DJF. (c) JJA.
