James I.N. Introduction to Circulating Atmospheres
Подождите немного. Документ загружается.


3.5 Problems 79
further, that the upper level flow is close to 30kPa and that the ascent and
descent processes are adiabatic, use the first law of thermodynamics to
estimate the pole-equator temperature difference. Look up a cross section
of
[6]
(given in Fig.4.2) to check and comment upon your result.

4
The zonal mean meridional circulation
4.1 Observational basis
The large scale structure of the atmospheric flow varies most rapidly in the
vertical direction, and least rapidly in the zonal direction. Zonal averaging
therefore makes the important vertical and meridional variations plain, and
has been employed for many years as a compact way of studying the global
circulation. Indeed, for many writers, the global circulation is simply the
pattern of flow projected on to the meridional plane. In this book, we will
take a broader view by attempting to summarize our current understanding
of the full, evolving three-dimensional pattern of winds and temperature in
the atmosphere. But the traditional zonal mean view is a useful starting
point which we will explore in this chapter.
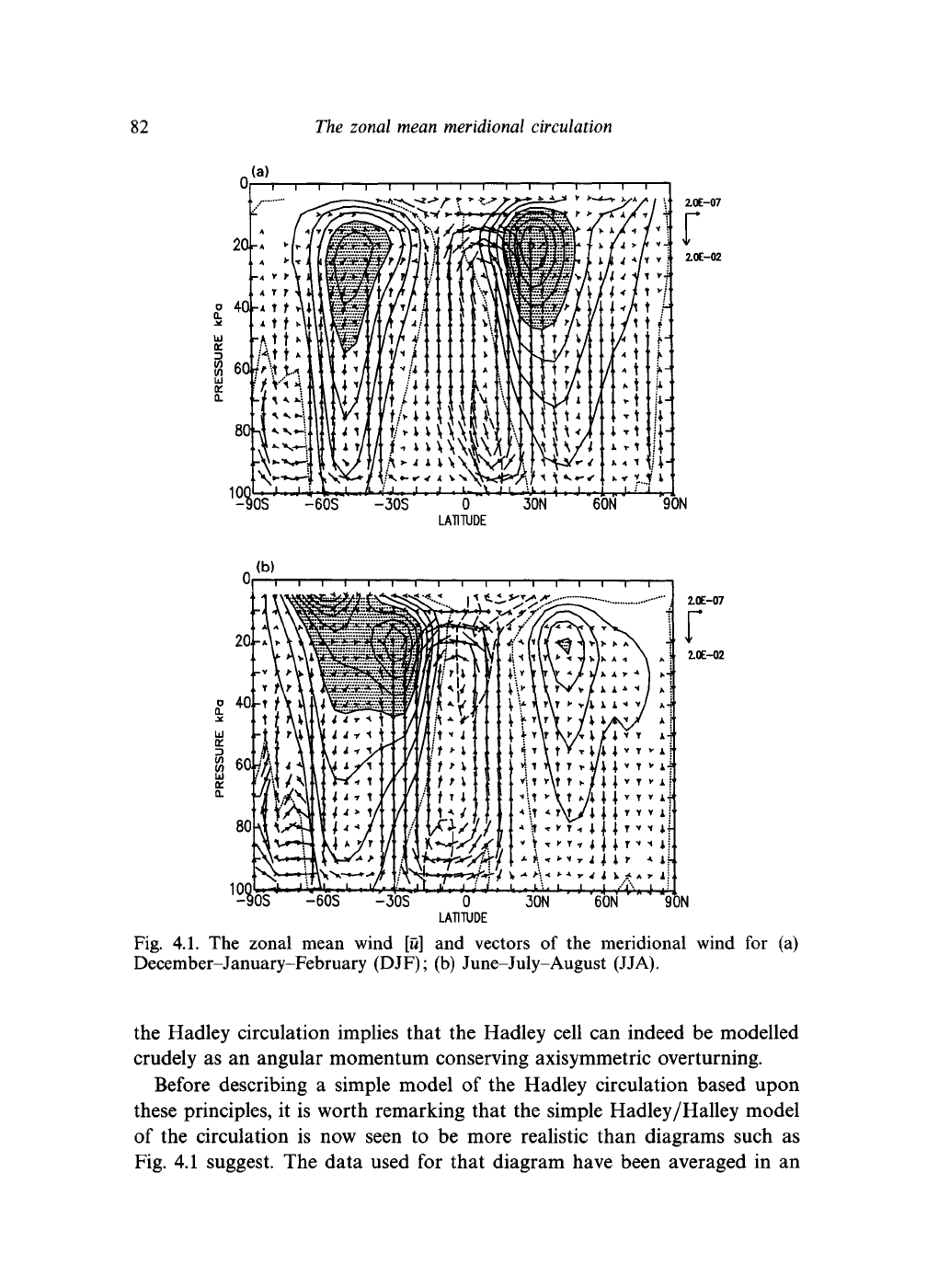
The zonal mean wind and vectors of the mean meridional wind are
illustrated in Fig. 4.1, based on ECMWF analyses. Rising motion is seen in
the tropics, with the maximum vertical velocity in the summer hemisphere.
Strongest descent is at latitudes of around
25 — 30 °
in the winter hemisphere,
with flow towards the equator near the surface and away from the tropics in
the upper troposphere, as is required by continuity. Such an axisymmetric
circulation is the most obvious response of the atmospheric flow to the net
heating excess in the tropics and the deficit at high latitudes discussed in
the preceding chapter. Halley, in 1689, and Hadley, in 1735, both suggested
the existence of such a circulation in order to account for the trade winds
blowing towards the equator at the surface. Their work is of great historical
importance, representing some of the first attempts to account for the global
circulation in terms of simple physically based models.
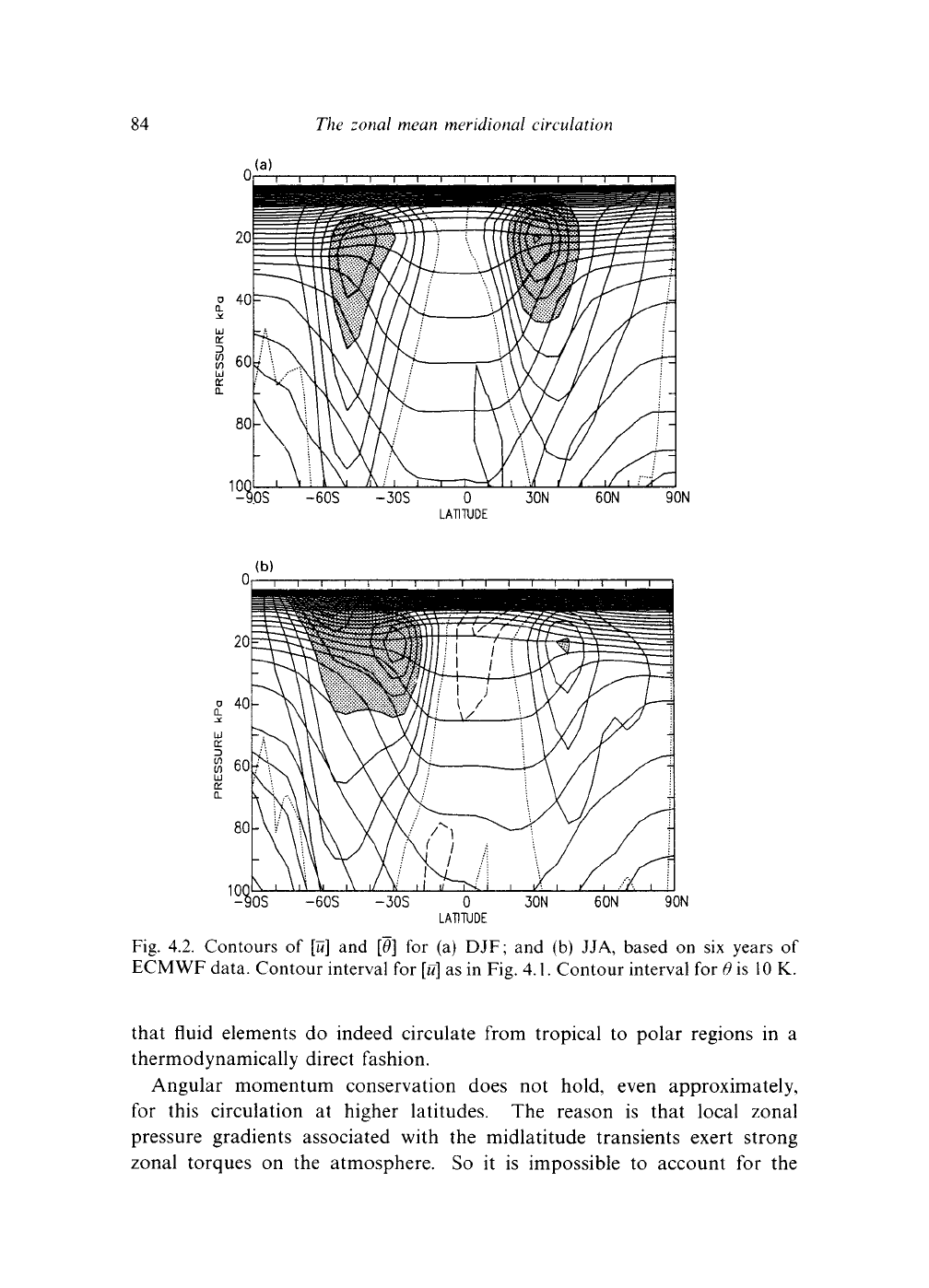
The pattern of zonal wind
[u]
is closely related to the distribution of poten-
tial temperature [0]. This is illustrated by Fig. 4.2, which shows the same
80

4.1
Observational basis
81
contours of
[u]
as Fig. 4.1, but with contours of potential temperature, [6].
The DJF and JJA cases are shown for completeness. Thermal wind balance,
Eq. (1.53), holds to a good approximation for the zonal mean state. Hence,
strong horizontal temperature gradients are related to strong vertical wind
shears throughout middle and high latitudes. In the tropics, the horizontal
temperature gradients are small; since / tends to zero also, the wind is not
determined by the thermal wind relationship in the deep tropics.
Comparison of Figs. 4.1 and 4.2 shows that the low latitude Hadley
circulation has ascent where the temperature is greatest, and descent where
it is less. By the arguments of Chapter 3, such a circulation will generate
kinetic energy; it is termed 'thermally direct'. Thermally direct circulation
is also seen at high latitudes, especially in the winter southern hemisphere.
In the midlatitudes, the mean meridional circulation is 'thermally indirect'.
This axisymmetric thermally direct overturning is absent in the midlatitudes;
there it is replaced by a thermally indirect circulation which is called the
'Ferrel cell'. Thermodynamically, this cell, characterized by descent in warm
regions and ascent in colder regions, represents a sink of kinetic energy.
It must be forced by some form of mechanical stirring. Its study led to a
considerable emphasis being placed on the role of the midlatitude eddies in
driving the circulation, especially by Victor Starr and his coworkers at MIT
in the 1940s and 1950s.
The confinement of the Hadley circulation to the tropics is related to
the rotation of the Earth. Nearly inviscid axisymmetric motion would tend
to conserve angular momentum with the result that unrealistically strong
zonal winds would develop in the upper troposphere poleward of
20 °
or so.
Defining the specific angular momentum of a ring of air at latitude
<j>
as
(Qacos
(j)
+ [w])acos 0, conservation of angular momentum for a ring whose
zonal velocity is zero at the equator implies that the zonal wind at other
latitudes is given by:
[u] == Qa
sin
2
<\>/
cos
(j).
(4.1)
It can quickly be verified that this formula suggests winds of
56
m s"
1
at
20° and
127
m s"
1
at 30° of latitude. Nevertheless, a consideration of
the diagram suggests that while angular momentum conservation is clearly
a hopeless description of the zonal wind throughout middle and higher
latitudes, the upper tropospheric wind in the tropics and subtropics does
indeed vary in a way which is reminiscent of Eq. (4.1). It increases in
a roughly quadratic fashion away from the equator, with a maximum of
35-40 m s"
1
in the so-called subtropical jet. The fact that this subtropical
jet maximum coincides with the poleward limit of the upper branch of
82
The zonal mean meridional circulation
0
LATITUDE
60N
2.0E-07
ZOE-02
90N
0
LATITUDE
60N
ZOE-07
ZOE-02
90N
Fig. 4.1. The zonal mean wind [u] and vectors of the meridional wind for (a)
December-January-February (DJF); (b) June-July-August (JJA).
the Hadley circulation implies that the Hadley cell can indeed be modelled
crudely as an angular momentum conserving axisymmetric overturning.
Before describing a simple model of the Hadley circulation based upon
these principles, it is worth remarking that the simple Hadley/Halley model
of the circulation is now seen to be more realistic than diagrams such as
Fig. 4.1 suggest. The data used for that diagram have been averaged in an
4.1 Observational basis 83
ZOE-07
ZOE-02
0
LATITUDE
90N
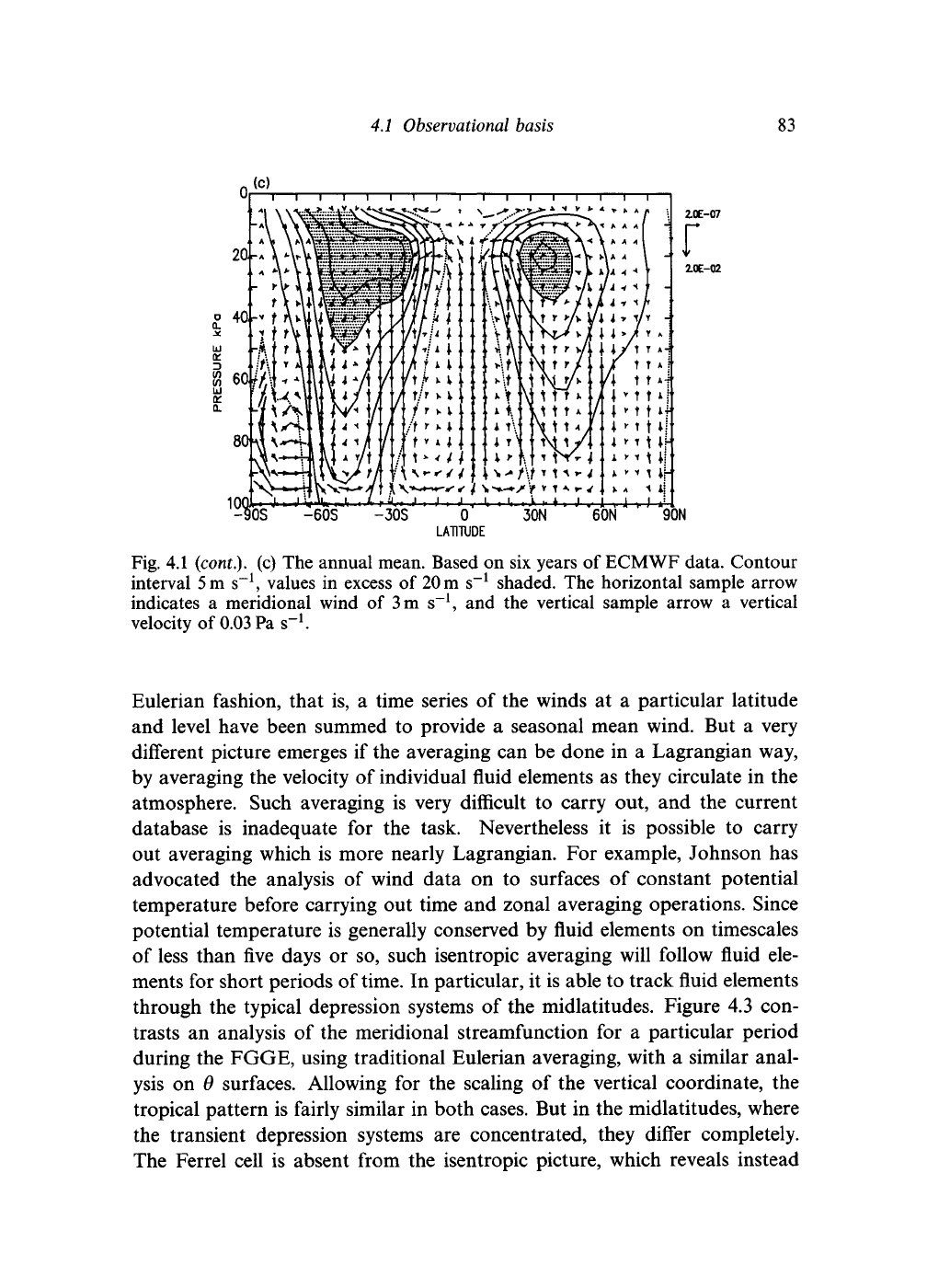
Fig. 4.1 (cont). (c) The annual mean. Based on six years of ECMWF data. Contour
interval
5 m
s"
1
, values in excess of
20 m
s"
1
shaded. The horizontal sample arrow
indicates a meridional wind of
3
m s"
1
, and the vertical sample arrow a vertical
velocity of
0.03
Pa s"
1
.
Eulerian fashion, that is, a time series of the winds at a particular latitude
and level have been summed to provide a seasonal mean wind. But a very
different picture emerges if the averaging can be done in a Lagrangian way,
by averaging the velocity of individual fluid elements as they circulate in the
atmosphere. Such averaging is very difficult to carry out, and the current
database is inadequate for the task. Nevertheless it is possible to carry
out averaging which is more nearly Lagrangian. For example, Johnson has
advocated the analysis of wind data on to surfaces of constant potential
temperature before carrying out time and zonal averaging operations. Since
potential temperature is generally conserved by fluid elements on timescales
of less than five days or so, such isentropic averaging will follow fluid ele-
ments for short periods of
time.
In particular, it is able to track fluid elements
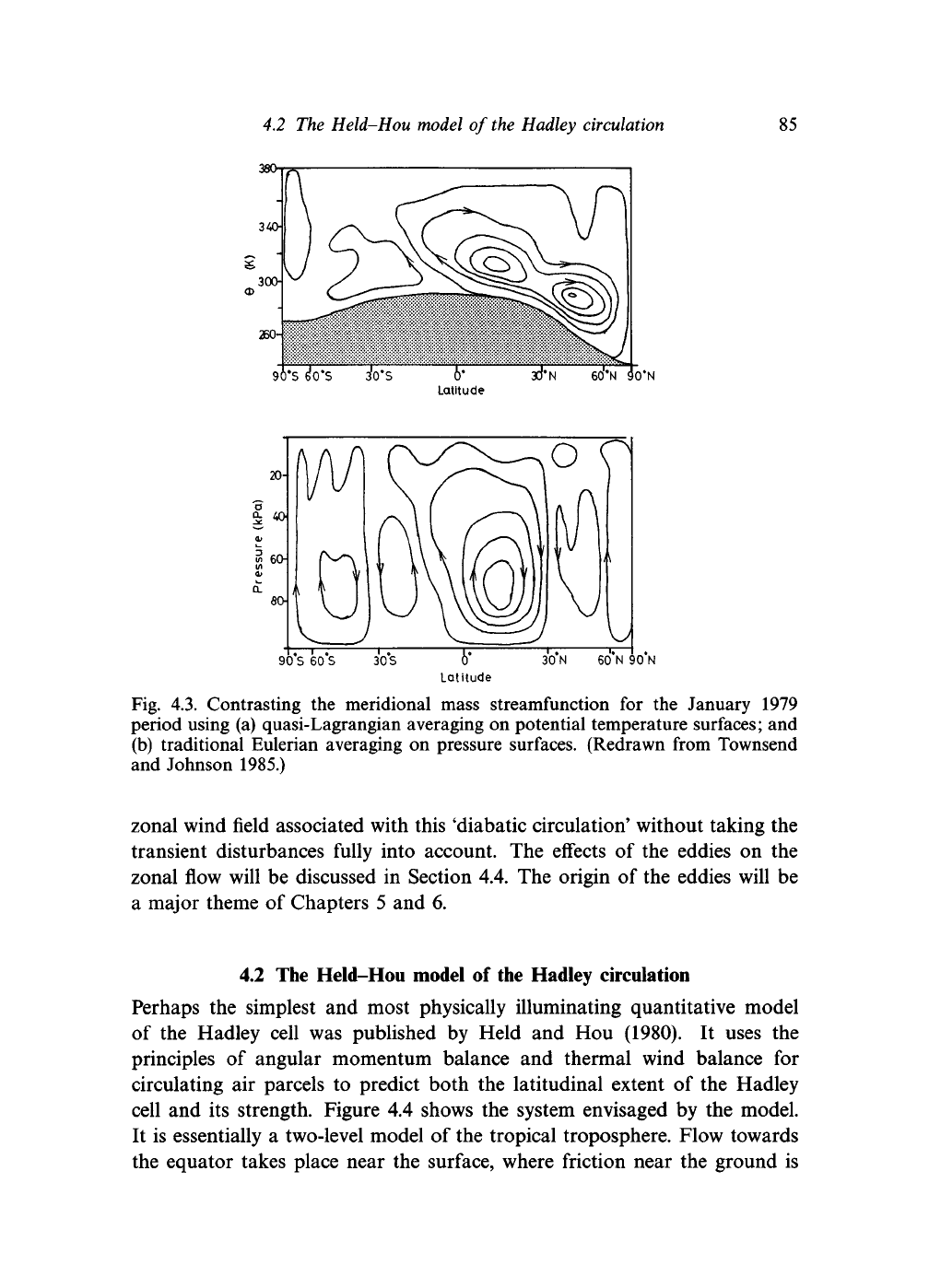
through the typical depression systems of the midlatitudes. Figure 4.3 con-
trasts an analysis of the meridional streamfunction for a particular period
during the FGGE, using traditional Eulerian averaging, with a similar anal-
ysis on 6 surfaces. Allowing for the scaling of the vertical coordinate, the
tropical pattern is fairly similar in both cases. But in the midlatitudes, where
the transient depression systems are concentrated, they differ completely.
The Ferrel cell is absent from the isentropic picture, which reveals instead
84
The zonal mean meridional circulation
-60S
-30S
0
LATITUDE
30N 60N
90N
Fig. 4.2. Contours of
[u]
and
[6]
for (a) DJF; and (b) JJA, based on six years of
ECMWF data. Contour interval for
[u]
as in Fig.
4.1.
Contour interval for 6 is 10 K.
that fluid elements do indeed circulate from tropical to polar regions in a
thermodynamically direct fashion.
Angular momentum conservation does not hold, even approximately,
for this circulation at higher latitudes. The reason is that local zonal
pressure gradients associated with the midlatitude transients exert strong
zonal torques on the atmosphere. So it is impossible to account for the
4.2 The Held-Hou model of the Hadley circulation 85
90*5 60*5 30'S 6'
Latitude
30*N 60'N 90'N
20-
40-
?
60-
fiO-
o c
90S 60S 30 S
30
N
60
N
90
N
Latitude
Fig. 4.3. Contrasting the meridional mass streamfunction for the January 1979
period using (a) quasi-Lagrangian averaging on potential temperature surfaces; and
(b) traditional Eulerian averaging on pressure surfaces. (Redrawn from Townsend
and Johnson 1985.)
zonal wind field associated with this 'diabatic circulation' without taking the
transient disturbances fully into account. The effects of the eddies on the
zonal flow will be discussed in Section 4.4. The origin of the eddies will be
a major theme of Chapters 5 and 6.
4.2 The Held-Hou model of the Hadley circulation
Perhaps the simplest and most physically illuminating quantitative model
of the Hadley cell was published by Held and Hou (1980). It uses the
principles of angular momentum balance and thermal wind balance for
circulating air parcels to predict both the latitudinal extent of the Hadley
cell and its strength. Figure 4.4 shows the system envisaged by the model.
It is essentially a two-level model of the tropical troposphere. Flow towards
the equator takes place near the surface, where friction near the ground is
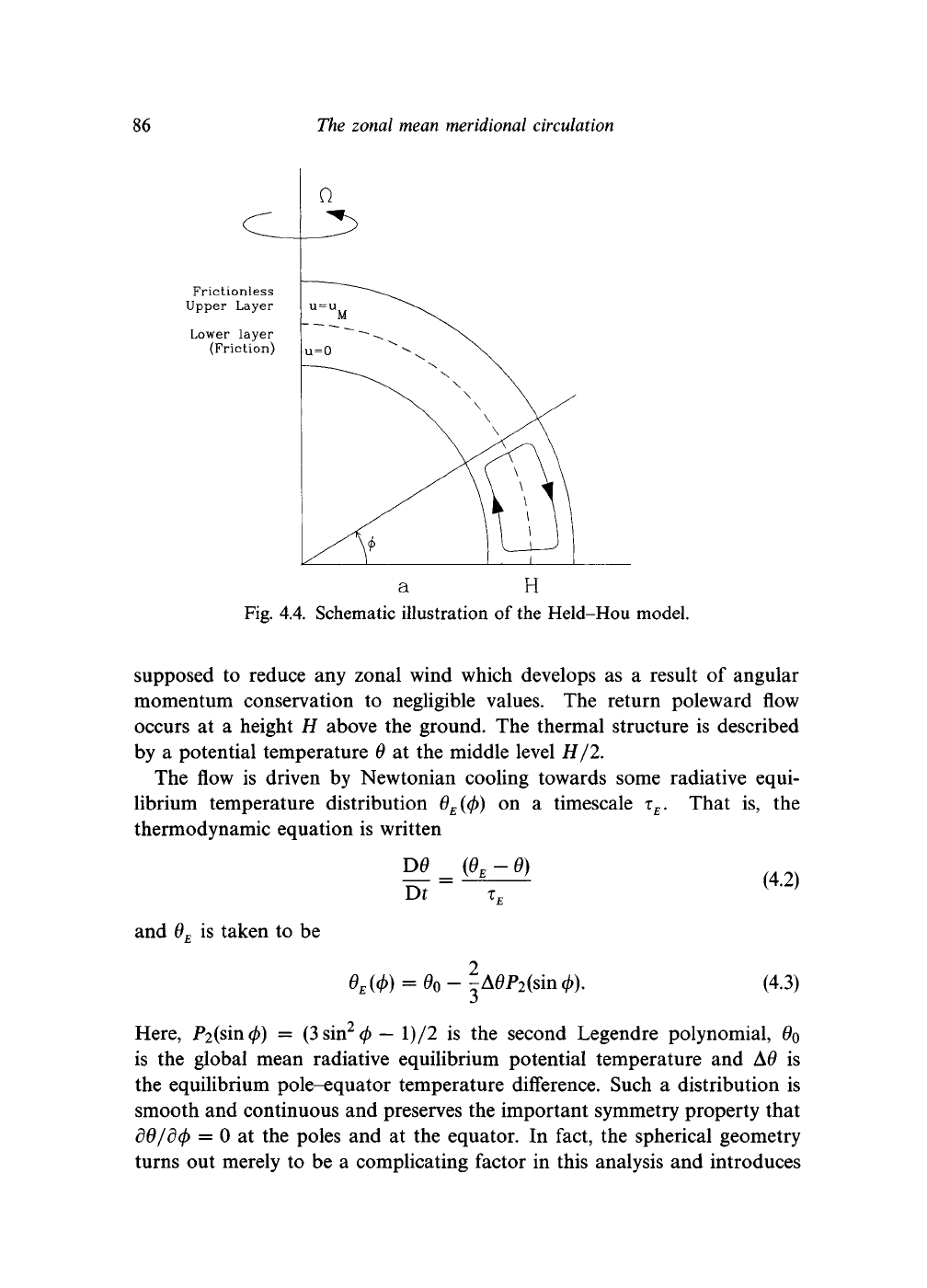
86
The zonal mean meridional circulation
Frictionless
Upper Layer
Lower layer
(Friction)
a
H
Fig. 4.4. Schematic illustration of the Held-Hou model.
supposed
to
reduce any zonal wind which develops
as a
result
of
angular
momentum conservation
to
negligible values. The return poleward flow
occurs
at a
height
H
above the ground. The thermal structure is described
by
a
potential temperature 9 at the middle level H/2.
The flow
is
driven by Newtonian cooling towards some radiative equi-
librium temperature distribution 0
£
(</>)
on a
timescale T
E
. That
is, the
thermodynamic equation is written
(4.2)
and 9
E
is taken to be
Dd
Dt
n
_(e
E
2
°~3
l
-d)
^E
\vr2[
(4.3)
Here, P2(sin0)
=
(3sin
2
(/>
—
l)/2
is
the second Legendre polynomial,
#o
is the global mean radiative equilibrium potential temperature and A9
is
the equilibrium pole-equator temperature difference. Such
a
distribution
is
smooth and continuous and preserves the important symmetry property that
d9/d(f>
=
0
at
the poles and
at
the equator. In fact, the spherical geometry
turns out merely to be
a
complicating factor in this analysis and introduces

4.2 The Held-Hou
model
of
the
Hadley
circulation
87
no new physical principle into the model; accordingly, we will assume that
(j)
= y/a is so small that sine/) can be replaced by y/a. Equation (4.3) is
therefore conveniently rewritten
The actual temperature distribution will differ from this radiative equi-
librium distribution, with advection by the air motion balancing the diabatic
tendencies implied by Eq. (4.2). The essence of the Held-Hou model is in
predicting the actual temperature from angular momentum balance con-
siderations. Assume the wind at the upper level is given by Eq. (4.1) which
in the small latitude limit becomes
U
M
=
^f- (4.5)
The subscript M reminds us that this is a zonal wind derived on the basis
of angular momentum conservation. The low level zonal wind is taken to be
zero as a result of friction. Then
Jz =
\
=
%•
(46)
But the vertical wind shear is related to the horizontal temperature gradi-
ent by the thermal wind relationship. Under the assumption of steady
axisymmetric flow and hydrostatic equilibrium, thermal wind balance must
hold even at low latitudes (see Eq. (1.53)). In the present notation, and using
height as the vertical coordinate, it can be written
or substituting for du/dz from Eq. (4.6):
By integrating this relation, the actual potential temperature distribution
required by this pattern of zonal wind is
0 0
Q20
° v
4
(4 9)
Once more, the subscript M emphasizes that this potential temperature
distribution was derived using angular momentum conservation arguments.
The constant 6
M0
is a constant of integration which has yet to be determined;

The zonal mean meridional circulation
20°S
10°S
Fig. 4.5. Showing 6
E
and 6
M
as a function of poleward distance for the Held and
Hou model. 0
m
must be chosen so that the areas between the two curves are equal,
i.e., so that there is no net heating of air parcels.
it represents the equatorial temperature and we anticipate that the heat
transport by the Hadley cell means that it will be less than 9
E0
.
The distributions of
9
E
and 9
M
are compared in Fig. 4.5. The temperature
profile is much flatter than the radiative equilibrium profile close to the
equator. At higher latitudes, it falls off more rapidly. A suitable choice of
9
m
means that there is heating between the equator and the first crossing
point of the curves and cooling between the first and second crossing points.
At higher latitudes, heating is implied; clearly this is thermodynamically
impossible and so we conclude that poleward motion ceases at this second
crossing point, which must represent the poleward limit of the Hadley
circulation; its latitude is denoted Y. At higher latitudes, 9 = 9
E
in this
strictly axisymmetric model. The latitude of the poleward edge of the cell, 7,
is determined by choosing 9
m
so that there is no net heating of circulating
air parcels, so that (from Eq. (4.2)):
L
