Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.


278 Chapter 6
and the general evolution equations of homogeneous and non-homogeneous
reward processes in the immediate case are respectively given by:
()
()
11 1 11
11 1
11
() () () () () ()
( ) ( ) (1 )(1 ()) () ()
(1 ( )) ( ) ( ) ( ),
mt mt
iikik ikik
kk
mt t
ik k i i
k
mt
iikik
k
Vt b b
bVt swpe Ht
swpe H t t
ϑ
ε
εε
ϑτ ϑ
ε
εε
ϑ τ
ε
τ
ϑψτντ ϑγϑνϑ
ϑ
ϑν ϑ ψ τν τ
ϕψτντ
== = ==
== =
==
=+
+−+−−
+−
∑∑ ∑ ∑∑
∑∑ ∑
∑∑
(7.5)
() ()
11
1
11 11
1
(,) (1 (,)) (,) (, ) (, )
(1 )(1 ( , )) ( , ) ( , )
(, ) ( ,) , (, ) (, ) ,
(, ) (, ) (, )
mt
iiikik
ks
t
ii
s
mt mt
ik k ik ik
ks ks
ik ik
s
Vst swpe Hst st s s
swpe H s t s s
bs V t s bs s s
bs s s
ε
ε
τ
ε
τ
ε
εε
ϑϑ
ϑ
ε
ϑτ
ϕψτντ
ψτντ
ϑ
ϑν ϑ ϑγ ϑν ϑ
ϑψτντ
==+
=+
==+ ==+
=+
=−
+− −
++
+
∑∑
∑
∑∑ ∑∑
∑
11
,
mt
ks==+
∑∑
(7.6)
where:
1
() ()(),
n
j
j
j
Vt Vt
ε
βεβ
θ
φθ θ
=
−= −
∑
(7.7)
1
(,) (,) (,),
n
j
j
j
Vt sVt
ε
βεβ
θφθθ
=
=
∑
(7.8)
given that r
ε
was the implied interest rate at time 0.
Let us point out that in relation (7.7), the term ( )
j
Vt
β
θ
−
represents the RMPV of
all the rewards paid or received in a time t
θ
−
, given that the system is in state
S
β
and the interest rate is
j
r .
At starting time 0 of our study, the known interest rate was
r
ε
. The system
evolves for a time
θ
and gets the interest
j
r with the probability ( )
j
ε
φ
θ
.
To compute the mean RMPV, we first need to compute the expected value (7.7)
and then to use the general formula.
Similar arguments can be used for relation (7.8) in the non-homogeneous case.
Furthermore if we don’t know the interest rate at the initial moment, it results
that:
1
() (),
n
ii
Vt pV t
ε
ε
ε
=
=
∑
(7.9)
Finance and Insurance models 279
1
(,) () (,),
n
ii
Vst p sV st
ε
ε
ε
=
=
∑
(7.10)
where:
12
,,,
n
p
pp… (7.11)
and
12
(), (), , ()
n
p
sps ps… (7.12)
are the initial probability distributions of the r.v. interest rate respectively at time
0 in the homogeneous case and at time
s in the non-homogeneous one.
In the non-homogeneous case if (7.12) is unknown, we can work in the following
way:
1
(0, ) (0,0) (0, )
n
ii
p
sp s
εε
ε
φ
=
=
∑
(7.13)
where (0,0)
i
p are the elements of initial probability distribution and should be
known.
The related due cases are given by:
()
()
1
11 0 11
1
11 0
1
10
() () () () () ()
( ) ( ) (1 )(1 ( )) ( ) ( )
(1 ( )) ( ) ( ) ( ),
mt mt
iikik ikik
kk
mt t
ik k i i
k
mt
iikik
k
Vt b b
bVt swpe Ht
swpe H t t
ϑ
ε
εε
ϑτ ϑ
ε
εε
ϑ τ
ε
τ
ϑψτντ ϑγϑνϑ
ϑ
ϑν ϑ ψ τν τ
ϕψτντ
−
== = ==
−
== =
−
==
=+
+−+−−
+−
∑∑ ∑ ∑∑
∑∑ ∑
∑∑
(7.14)
()
1
1
1
11
1
11
(,) (1 (,)) (,) (, ) (, )
(, ) (, ) (, )
(1 )(1 ( , )) ( , ) ( , )
(,) (,) , (,) (,)
mt
i i ik ik
ks
mt
ik ik
ks s
t
ii
s
mt
ik ik ik k
ks
Vst swpe Hst st s s
bs s s
swpe H s t s s
bs s s bs V t
ε
ε
τ
ϑ
ε
ϑτ
ε
τ
ε
εε
ϑ
ϕψτντ
ϑψ τντ
ψτντ
ϑγ ϑν ϑ ϑ ϑ ν
−
==
−
==+ =
−
=
==+
=−
+
+− − +
+
∑∑
∑∑ ∑
∑
∑∑
()
11
,.
mt
ks
s
ϑ
ϑ
==+
∑∑
(7.15)
In the due case, equations (7.7) and (7.8) become:
1
() ()(),
n
j
j
j
Vt Vt
ε
βεβ
θ
φθ θ
=
−= −
∑
(7.16)
1
(,) (,) (,).
n
j
j
j
Vt sVt
ε
βεβ
θφθθ
=
=
∑
(7.17)
At last it results that:
280 Chapter 6
1
() (),
n
ii
Vt pV t
ε
ε
ε
=
=
∑
(7.18)
1
(,) () (,).
n
ii
Vst p sV st
ε
ε
ε
=
=
∑
(7.19)
To apply this model we should, in both immediate and due cases, solve the two
different evolution equations, the first for the rate of interest and the other one for
the reward process. These equations are obtained with two independent data sets.
Furthermore, in the solution of the two different evolution equations it is
supposed that the two phenomena are independent. But this is not a strong
hypothesis because it is obvious that the interest rate structure doesn’t depend
upon the evolution of an illness.
In conclusion, the semi-Markov reward models presented in this last section are
quite general and can take into account two random evolutions, one for the
interest rate and the other for the evolution of the actuarial phenomena and
constitute strong models for real life applications.
Chapter 7
INSURANCE RISK MODELS
In this chapter, we will first recall the main classical models in risk theory which
are useful for insurance companies and then extend them fully to the semi-
Markov case. To avoid confusion we adopt the classical actuarial notation of risk
theory
1 CLASSICAL STOCHASTIC MODELS FOR RISK
THEORY AND RUIN PROBABILITY
In this section, we will develop Example 4.1 of Chapter 3, first into a general
case, and then into the particular case of a Poisson process for claim arrivals.
Let us consider an insurance company, beginning at time 0 with an initial capital
of amount u (u > 0), also called reserve for insurance companies or equity for
banks.
In almost all developed countries, this initial reserve has a minimal amount fixed
by the government and depending on the turnover of the insurance company.
Indeed, it is clearly understood that this capital protects customers against the
possibility that an unlucky company would have to pay a lot of large claims in a
short period of time, for example for a catastrophic event, and not be liquid
enough to do so.
A basic problem, in general solved by actuaries, is to give an objective value for
this minimal reserve. We will learn later how to solve this fundamental problem.
Any risk model related to an insurance company is characterized by three "basic"
processes:
(i) the first one is the claim number process. This is a stochastic process giving
the counting process of claims occurring to the customers;
(ii) the second stochastic process concerns the claim amounts. In particular, it
gives the distribution of what the company has to pay when a claim occurs;
(iii) the last process is related to the income of the company; and it is generally a
deterministic process since the premiums paid by the customers must be known
at the origin of the individual contracts.
To any set of assumptions about these three processes, there corresponds a
particular stochastic risk model. The most important will be presented later.
This section will only be concerned with two models: the so-called G/G model or
the E.S. Andersen model, and the P/G model or the Poisson or Cramer-Lundberg
model. The notation, borrowed from queuing theory, gives information
282 Chapter 7
concerning the two d.f. used in these models, one for the interarrival and the
other one for the claim amounts (G for general means any d.f. and P, for Poisson,
a negative exponential distribution
1.1 The G/G Or E.S. Andersen Risk Model
1.1.1 The Model
The basic assumptions for the G/G model are:
(i) The claim number process
Let
(, 1)
n
Xn≥ represent the stochastic process of interarrival times between
successive claims. We will suppose that this process is a sequence of i.i.d. non -
negative random variables with A as common d.f., such that:
a) A(0) < 1, (1.1)
b)
0
() .xdA x
α
∞
=
<∞
∫
(1.2)
(ii) The claim amount process
Let
(, 1)
n
Yn≥ represent the sequence of successive claim amounts. Here too, we
will suppose that we have a random sequence of non-negative i.i.d. random
variables with B as common d.f., such that:
a) B(0) < 1, (1.3)
b)
0
() .ydB y
β
∞
=
<∞
∫
(1.4)
Moreover, the sequences ( , 1)
n
Xn≥ and ( , 1)
n
Yn≥ are independent and defined
on a complete probability space
(,,)P
Ω
ℑ .
(iii)
The premium income process
The classical assumption is that there is a constant, of course positive, premium
rate c per unit of time, which means that in the time period [0,t], the total amount
of income for the company is ct.
1.1.2 The Premium
One of the major problems for the company is how to fix the premium rate
"fairly" while respecting two conditions:
a) the lifetime of the company, that is the period in which its capital is always
positive, must be, with a very large probability, as long as possible.
Indeed from the economic point of view, large reserves constitute a factor of
security but excessive reserves may signify that the premiums are too high.

Insurance risk models 283
b) It is in the best interest of each company to choose c as low as possible but
without infringing upon its own economic security.
To fix the value of c, let us consider the renewal process ( , 0)
n
Tn≥ of claim
arrival times related to the sequence ( , 1)
n
Xn≥ , with X
0
=0 a.s.. That is:
0
.
n
nk
k
TX
=
=
∑
(1.5)
Using renewal theory, the associated counting process ( ( ), 0)Nt t≥ defined by
(2.3) of Chapter 2, gives the total number of claims in (0,t] and from
Corollary
4.2
, Chapter 2, relation (4.26), we know that:
() 1
lim
t
Ht
t
α
→∞
=
(1.6)
if
() ( ())Ht ENt
=
(1.7)
and so, for large t:
(()) .
t
ENt
α
≈ (1.8)
Now, from relation (1.4) the mean cost of the total number of claims in (0,t]
is approximately:
t
β
α
. (1.9)
This last result shows that the mean total cost of claims having to be paid by the
insurance company during the period (0,t] is approximately given by
ct
, where:
.c
β
α
=
(1.10)
It follows that if we take this value
c
as the constant premium rate per unit of
time, we have what is called a game, "insurance company-customers" which is
asymptotically fair. That is why
c
is called the
pure premium.
But, unfortunately, we will see later that this choice leads to the ruin of the
company a.s. on
[
)
0,∞ . Also, it is necessary to introduce a positive security
loading
η
such that:
(1 )
cc
η
=
+
(1.11)
or
(1 ) .c
β
η
α
=+ (1.12)
In other words, the company must choose the premium rate
c such that:
.c
β
α
> (1.13)
Now,
c
is called the loading premium.
284 Chapter 7
So, if we set c = 1, this relation implies the assumption:
α
β
> , (1.14)
i.e., the mean interarrival time between two successive claims is larger than the
mean claim amount.
Intuitively, this condition warrants good service to the policy holders and it will
be theoretically justified below.
In conclusion, we can state that each insurance company has to
control two basic
parameters: its
initial reserve or equities u and its security loading .
η
Moreover,
the possibilities open to the insurance companies are dictated by law.
1.1.3 Three Basic Processes
We will now introduce three stochastic processes of fundamental importance in
risk theory.
1) The accumulated claim amount process
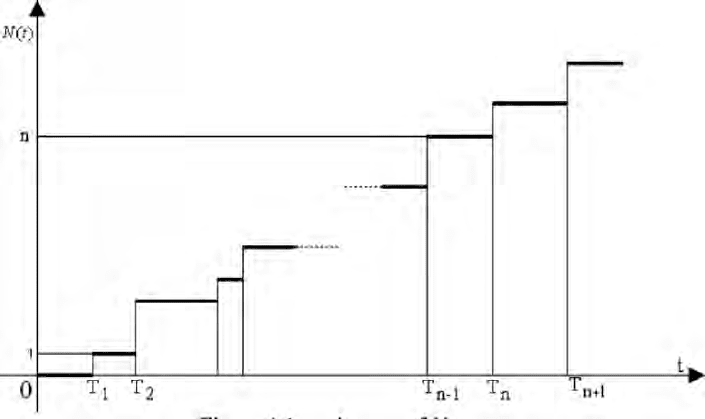
It is the stochastic process ( ( ), 0)Ut t
≥ defined as:
()
1
()
Nt
n
n
Ut Y
=
=
∑
(1.15)
or as:
()
()
Nt
Ut U
=
(1.16)
if
1
,
n
ni
i
UY
=
=
∑
(1.17)
always using the classical convention that the value of a sum over a void set is
zero.
For every fixed t, U(t) gives the total number of claims on (0,t].
Let us denote by M(t,y) the value of the d.f. of U(t) at y; we can then write:
0
(, ) ( , () )
n
n
M
ty PU yNt n
∞
=
=
≤=
∑
. (1.18)
Using relation (3.5) of Chapter 2, the independence assumption of the two
stochastic processes
(, 1)
n
Xn≥
and
(, 1)
n
Yn≥
leads to:
0
() ( 1) ()
n=0
(, ) ( ) ( () )
= ( ( ) ( )) ( ).
n
n
nnn
Mty PU yPNt n
At A tB y
∞
=
∞
+
=≤ =
−
∑
∑
(1.19)
2) The risk process
It is the stochastic process:
Insurance risk models 285
(() , 0)Ut ctt
−
≥ (1.20)
representing the total net outcome of the company up to time t, provided it is still
alive at this time.
3) The risk reserve process (or the surplus process)
It represents the stochastic process ( ( ), 0)tt
α
≥ , where:
() () , 0.tuUtctt
α
=
−+≥ (1.21)
It gives, at time t, the total net asset of the company supposing the company is
still alive at time t.
The next two figures give typical trajectories of the N process and the
α
process.
Figure 1.1: trajectory of N process
1.1.4 The Ruin Problem
We come now to the fundamental ruin problem in risk theory.
From a strict economic point of view, the lifetime of the insurance company may
be defined as the stopping time:
{
}
inf : ( ) 0 .Ttt
α
=< (1.22)
This is a "strict" point of view, as we do not consider the possibility for the
company to take out a loan to cover a "small" ruin.
Clearly, if the event
{
}
:() 0T
ωω
≤
occurs, then the company is ruined before or
at time t; otherwise the company is still alive at time t.

286 Chapter 7
Figure 1.2: trajectory of
α
process
We will use the following notation for the probabilities of ruin and non-ruin on
an infinite time horizon, i.e. on
[
)
0,
∞
:
() ( (0) ),uPT u
α
Ψ= <∞ = (1.23)
() ( (0) ) 1 ().uPT u u
φα
==∞ ==−Ψ (1.24)
The knowledge of Ψ or equivalently of
φ
is necessary in order to select values
for parameters u and for
η
to warrant good services for the customers.
For example, if u is fixed, we can see the probability
φ
as a function of the
security loading
η
, say:
(, ).u
φ
η
(1.25)
If we impose the condition:
(, ) ,u
φ
ηε
> (1.26)
for example with
ε
=0.99999, we can select the minimum value of
η
such that
condition (1.26) is satisfied.
With the aid of results on random walk, we can now justify theoretically the fact
that a strictly positive security loading is a necessary condition for not having
ruin on
[
)
0,∞ a.s.
On the time period
(
]
1
,
nn
TT
−
, the liability of the company increases or decreases
by a net amount given by:
,1.
nn n
ZYcXn
=
−≥
(1.27)
Insurance risk models 287
The sequence of i.i.d. r.v.
(, 1)
n
Zn≥
(1.28)
generates a random walk of successive values:
1
.
n
nk
k
SZ
=
=
∑
(1.29)
From relation (1.21), we get:
()
nn
TuS
α
=
−
(1.30)
since S
n
is the risk process value at time T
n
.
Let us now consider the r.v. M defined by relation (17.27) of Chapter 3; from
relation (1.24), we deduce that:
() ( ).uPMu
φ
=
≤ (1.31)
From
Proposition 17.1 of Chapter 3, we know that the d.f. of M is non-
degenerate iff the random walk drifts toward
−
∞
, or equivalently iff:
()0.
n
EZ
<
(1.32)
It is now clear that this last condition is, from relation (1.27), also equivalent to
the inequality (1.13).
The case
0c
β
α
−
= (1.33)
must be treated carefully.
Indeed, in this case, the random walk generated by the random sequence (1.27)
oscillates, so that for any positive u, we have:
0
(:)1.
n
Pn S u
∃
∈>= (1.34)
In other words, this result shows that whatever the initial reserve is, the company
will be ruined with probability 1. This also means that the asymptotic fair game
leads a.s. to the ruin of the company.
So, without any loading, the random walk ( , 0)
n
Sn≥ will either drift toward +∞
or oscillate. In both cases, we know that a.s.
.M
=
∞ (1.35)
It follows that the problem of computing the non-ruin probability function
φ
only arises when inequalities (1.13) or (1.14) are satisfied, and it is necessary to
particularize some basic assumptions in order to obtain more tractable analytical
expressions. This is possible in the case of the P/G or Cramer-Lundberg model.
1.2 The P/G Or CRAMER-LUNDBERG Risk Model
1.2.1 The Model
To obtain this particular risk model, it suffices to adapt the Andersen model
explained above in the following manner: we impose that the claim amount
process is a Poisson process or as in
Example 3.1, Chapter 2 that:
