Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.


298 Chapter 7
0
0, 0,
()
1, 0.
u
u
u
≥
⎧
Ψ=
⎨
≤
⎩
(1.107)
By induction, we get successively:
1
00
()
00
()
00
0
() ( ) ()
( )
( )
( ).
t
nn
tRucty
Ru Rc t Ry
Ru Ry
uedtuctydBydt
edt e dBydt
eedtedBy
eedBy
Rc
λ
λ
λ
λ
λ
λ
λ
λ
∞∞
−
+
∞∞
−−+−
∞∞
−−+ −
∞
−−
Ψ= Ψ+−
≤
≤
≤
+
∫∫
∫∫
∫∫
∫
(1.108)
It suffices now to use the Cramer-Lundberg equation (1.100) to obtain the
desired result (1.101).
This last corollary shows the fundamental importance of inequality (1.101). The
knowledge of R gives to the insurer the possibility to adopt an informed, careful
attitude and it is well known that carefulness is one of the pillars of insurance.
The price to pay is just the resolution of the Cramer-Lundberg equation but that
is not a problem if we use the numerical Newton method.
However, the next two results show how to avoid this resolution in order to get
other upper bounds of the ruin probability.
Corollary 1.2
(i) Under the assumptions of Proposition 1.1, and if moreover, the variance
2
σ
related to the d.f. B, is supposed to be finite, then:
22
2( )
()
c
R
λ
β
λ
βσ
−
<
+
. (1.109)
(ii) If moreover the claim amount is, a.s., a bounded r.v. with M as upperbound,
then:
1
ln .
c
R
M
λβ
<
(1.110)
Proof
(i) This result is easily obtained by replacing
R
y
e in the equation (1.100) by its
development into a second-order MacLaurin series.
(ii) The function
R
y
ye being convex on
[
)
0,
∞
, we get from the convexity
inequality that:
0
1, 0 .
M
Rx RM Rx
xx x
ee xMe x
MM M
⎛⎞
≤+−≤≤ ≤
⎜⎟
⎝⎠
∫
. (1.111)
Coming back to the Cramer Lundberg equation (1.100), we obtain:
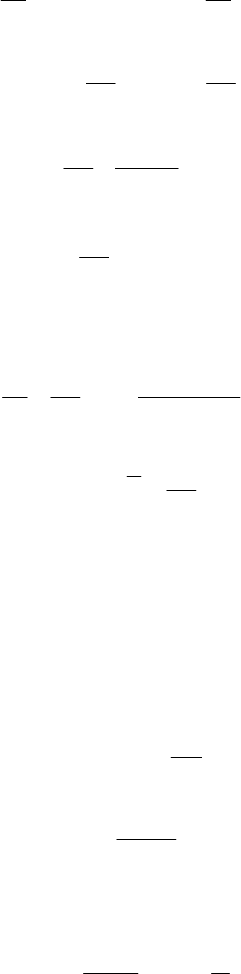
Insurance risk models 299
00
() (),
MM
RM
R
cxedBx xdBx
MM
λλ
λλ
+≤ +−
∫∫
(1.112)
so that:
.
RM
Rc e
M
M
λ
βλβ
λλ
+≤ +− (1.113)
It follows that:
1
,
RM
ce
RM
λβ
−
≤ (1.114)
and consequently:
,
R
M
c
e
λβ
≤ (1.115)
a result equivalent to the inequality (1.110) to be proved.
So, under the assumption that there exists a constant M such that B(M)=1, then
we have:
22
12()
ln .
()
cc
R
M
λ
β
λβ λ β σ
−
<<
+
(1.116)
In particular, by
Corollary 1.1, we have:
() ln .
t
M
c
te
λ
β
−
Ψ< (1.117)
This last inequality gives a useful upper bound of the ruin probability without
having to solve the Cramer-Lundberg equation. of course, as M tends toward
+
∞, we get the trivial bound 1.
Example 1.3 Let us suppose that the claim amount distribution is normal
2
(, ), 0
βσ β
> and with
μ
large enough so that the truncated normal is well
approximated by the entire normal curve.
From result (5.13) of Chapter 1, the Cramer-Lundberg equation (1.100) becomes:
22
2
.
R
R
Rc e
σ
β
λλ
+
+= (1.118)
Using a Taylor development of order 1, we get:
2
2
c
R
λ
β
σ
−
≈ . (1.119)
Example 1.4 (The adjustment coefficient for the P/P risk model)
In this case, we know that:
11
() ,0 .
1
B
ss
s
ϕ
β
β
=≤<
−
(1.120)
For this special case, the Cramer-Lundberg (1.100) equation takes the form:
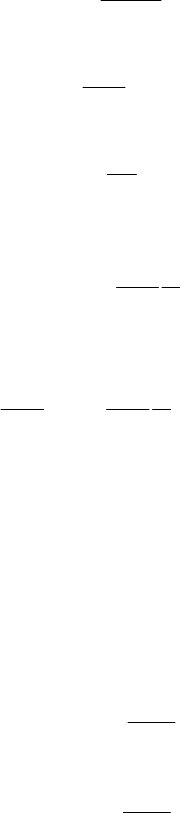
300 Chapter 7
.
1
Rc
R
λ
λ
β
+=
−
(1.121)
Therefore, the value of the adjustment coefficient is
1
R
η
β
η
=
+
(1.122)
where we know that:
1.
c
λ
β
η
=− (1.123)
This last result gives the following Cramer-Lundberg inequality (1.100) for the
P/P model:
() exp
1
u
u
η
ψ
η
β
⎛⎞
≤−
⎜⎟
+
⎝⎠
. (1.124)
Comparing with the exact value of
Ψ
given by relation (1.68), we see that this
majoration gives the overestimation:
exp .
11
u
ηη
η
ηβ
⎛⎞
−
⎜⎟
++
⎝⎠
(1.125)
Remark 1.1
(i) Economic interpretation of the adjustment coefficient
Using the exponential utility principle to cover the total outcome U(t) on the time
interval
[]
0,t , we can write:
() ()
()
aU t aP t
Ee e= (1.126)
where P(t) represents the mean global premium for the insurance company.
To find the value of the parameter a satisfying this last relation, let us first recall
that, from relation (1.19), we have:
()
0
()
(() ) ()
!
n
tn
n
t
PU t y e B y
n
λ
λ
∞
−
=
≤=
∑
. (1.127)
It follows that the generating function of the r.v. U(t) is given by:
()
0
(1 ( ))
()
() ()
!
.
B
n
sU t t n
B
n
ts
t
E
ee s
n
e
λ
λϕ
λ
ρ
∞
−
=
−−
=
=
∑
(1.128)
where the function
B
ρ
represents the generating function associated with the r.v.
Y
n
.
Consequently, the equality (1.126) is equivalent to:
(1 ( )) ( ).
B
taaPt
λ
ρ
−
−= (1.129)
We want to have a risk model for which the ratio P(t)/t is independent of t and
has as value c. Therefore, we must have from relation (1.129):
(1 ( ))
B
taact
λ
ρ
−
−=
, (1.130)

Insurance risk models 301
which is the Cramer Lundberg equation for the unknown parameter a, so that
a=R.
This result shows that if the choice is a linear income P(t) =ct, then a, the relative
marginal utility of the policyholder, is the constant R.
(ii) The adjustment coefficient and martingale theory
It is also possible to show that the adjustment coefficient R is the only value for a
such that the process
()
(,0)
aU t
et
−
≥ is a martingale with respect to the filtration
(, 0),
((), )
t
t
t
Us s t
σ
ℑ
≥
ℑ
=≤
(1.131)
and so, in particular:
()
().
R
Ut Ru
E
ee
−−
= (1.132)
2 DIFFUSION MODELS FOR RISK THEORY AND RUIN
PROBABILITY
There exist other risk models than those of type G/G. Models using semi-Markov
processes will be fully developed later.
In this section, we will briefly present two models using simple diffusion
processes (see Chapter 1).
2.1 The Simple Diffusion Risk Model
In this model (Cox and Miller (1965) and Gerber(1979)), we will immediately
model the risk reserve or the surplus process with a particular continuous time
stochastic process.
This means that the
α
process satisfies the very simple stochastic differential
equation:
(),
(0) .
ddtdWt
u
α
μσ
α
=
+
=
(2.1)
The process
((), 0)WWtt=≥is a standard Brownian motion defined on a
complete probability space
(,,)P
Ω
ℑ
and of course, we suppose that:
0, 0.
μ
σ
>> (2.2)
As in continuous time stochastic finance (see Merton(1999)), the first parameter
is called the trend and the second one the volatility.
This model gives a very simple expression for the
α
process:
() (), 0.ttWtt
α
μσ
=
+≥ (2.3)
With such a simple model, it is possible to compute the exact value of the ruin
probability (see Cox and Miller (1965)) on a finite time horizon [0,t], that is
(,) ( (0) )ut PT t u
ψα
=
<=, (2.4)
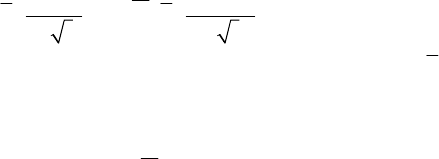
302 Chapter 7
with T defined by relation (1.22) and ( , )ut
ψ
by the following expression:
2
2
(,) 1 ,
u
ut ut
ut e
tt
μ
σ
μ
μ
ψφ φ
σσ
−
+−+
⎛⎞ ⎛ ⎞
=− +
⎜⎟ ⎜ ⎟
⎝⎠ ⎝ ⎠
(2.5)
where here, to avoid confusion with the notation for the non-ruin probability,
φ
represents the d.f. of a reduced normal r.v.
Let us point out that, letting t →∞, we get the following asymptotic result:
2
2
,0,
() lim (,)
1, 0.
u
t
e
uut
μ
σ
μ
ψψ
μ
−
→∞
⎧
⎪
>
==
⎨
⎪
<
⎩
(2.6)
Remark 2.1
a) From the result (2.5), we deduce that, for all positive u:
0
lim ( , ) 0
t
ut
ψ
→
=
. (2.7)
This is a simple consequence of the a.s. global continuity property of the
trajectories of the
α
process. That was not the case for the G/G risk model!
b) We also have:
(0, ) 1, 0tt
ψ
=
> (2.8)
and so:
(0) 1
ψ
=
, (2.9)
contrary to the result (1.116) for the Cramer-Lundberg or G/G risk model.
c) The asymptotic result (2.6) gives interesting information concerning the
strategic point of view of the insurance company.
Indeed, in this formula (2.6), the basic parameter is
2
2/
μ
σ
.
It gives a good measure of the two models of action available to the manager of
the company: increase or decrease the premiums, i.e. act on the trend
μ
, or
increase or decrease the risk by the mix of portfolio selection, i.e. act on the
volatility
.
σ
2.2 The ALM-like Risk Model (Janssen(1991),(1993))
In finance, it is usual to model the evaluation of the assets and the liabilities of a
bank or of an insurance company with the use of stochastic processes for both
parts of the balance sheet. This leads to useful models used in the theory and
practice of
asset liability management (in short ALM (Janssen (1991), (1993)).
We will now briefly present this type of model for an insurance company.
Let us represent by
((), 0), ((), 0)AAtt BBtt=≥=≥ (2.10)
successively the stochastic processes of the asset and of the liability under the
assumption that they satisfy the very simple stochastic differential system
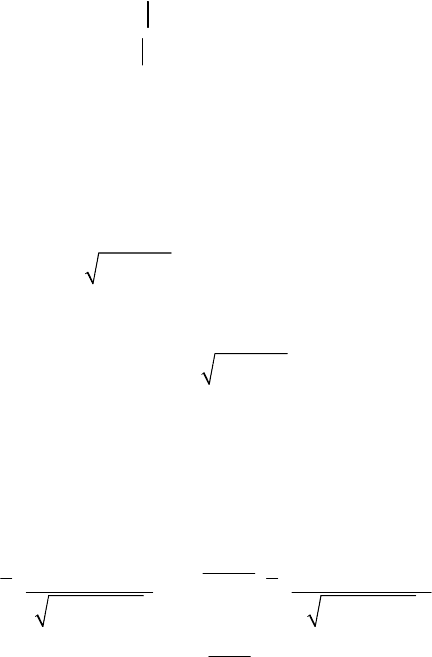
Insurance risk models 303
() (),
() (),
(0) , (0) 0
AAA
BBB
dA t dt dW t
dB t dt dW t
AuB
μσ
μσ
=+
=+
==
(2.11)
and where:
(i) , , , ,
AB AB
u
μ
μσσ
are strictly positive,
(ii)
((), 0), ((), 0)
AA BB
WWtt WWtt=≥=≥ are two independent standard
Brownian motions.
Clearly, the stochastic differential problem (2.11), has the following solution:
() (),
() ().
AAA
BBB
At u t W t
Bt t W t
μ
σ
μσ
=
++
=+
(2.12)
As above, we also have:
(,) ( (0) ),
() ( (0) ) lim (,).
t
ut PT tA u
uPT A u ut
ψ
ψψ
→∞
=≤ =
=≤∞ ==
(2.13)
From (2.12), we can write that:
() () () ().
AAA BBB
A
tBtu t Wt t Wt
μ
σμσ
−=++ −− (2.14)
The independence assumption between the two Brownian processes implies that
the process
(() (),0)
AB
AW t BW t t
−
≥ (2.15)
is probabilistically equivalent to the process
(
)
22
(), 0
AB
Wt t
σσ
+
≥ (2.16)
where the process W is a standard Brownian motion.
Let us now introduce two new parameters defined as:
22
,,
AB AB
μ
μμσ σσ
=− = + (2.17)
so that, using relation (2.14), we get
() () ().At Bt t W t
μ
σ
−
=+ (2.18)
Thus, we see that, with the change of parameters (2.17), the process ( )AB− is
modelled exactly like the simple diffusion risk model given by relation (2.3).
Consequently, all the results of subsection 2.1 are valid for the ALM-like model,
particularly the results (2.5), (2.6) giving here as results:
22
2
()
22 22
() ()
(,) 1 ,
() ()
AB
u
AB AB
AB AB
ut ut
ut e
tt
μ
σσ
μμ μμ
ψφ φ
σσ σσ
−
+
⎛⎞⎛ ⎞
+− −+−
⎜⎟⎜ ⎟
=− +
⎜⎟⎜ ⎟
++
⎝⎠⎝ ⎠
(2.19)
22
2
,,
() lim (,)
1 , .
AB
AB
u
AB
t
AB
e
uut
μμ
σσ
μ
μ
ψψ
μ
μ
−
−
+
→∞
⎧
⎪
>
==
⎨
⎪
<
⎩
(2.20)

304 Chapter 7
Remark 2.2
a) In addition to Remark 2.1, let us say that, with the ALM-like risk model, the
manager has more flexibility to measure the influence of strategic changes. This
is due to the fact that there are four parameters with two of them, ,
AA
μ
σ
only for
the asset part and the last two, ,
B
B
μ
σ
, only for the liability part.
b) For the ALM-like risk model, the basic parameter R becomes:
22
2
AB
AB
R
μ
μ
σ
σ
−
=
+
. (2.21)
It gives the possibility to correct a bad change, for example in the asset part with
an action on the liability part or vice-versa, and to introduce hedging strategies
for insurance companies (see Janssen, Bergendhäl (1999)).
2.3 Comparison Of ALM-Like And Cramer-Lundberg Risk
Models
It is interesting to see how "to adjust" an ALM risk model to a P/G or Cramer-
Lundberg model.
To do this, let us begin to consider a P/G model with as basic parameters , ,
λ
βη
.
From result (1.127), we know that the d.f. of U(t), the total claim amounts up to
time t, is given by
()
0
()
(() ) ()
!
n
tn
n
t
PU t y e B y
n
λ
λ
∞
−
=
≤=
∑
. (2.22)
From this expression, it results that:
0
()
(()) .
!
n
t
n
t
E
Ut e n t
n
λ
λ
β
λβ
∞
−
=
==
∑
(2.23)
Using the second Wald’s identity (Chapter 1, relation (6.59)), we also have
2
11
22
2
var( ( )) var( ) ( ( )) ( ( )) var( ( ))
= ,
Ut Y ENt EY Nt
tt
t
λσ λβ
αλ
=+
=+ (2.24)
2
σ
and
2
α
being respectively the variance and the centred moment of order 2
related to the d.f. B.
Let us note respectively by ,
CL ALM
α
α
the risk reserve processes related to the
Cramer-Lundberg model and the ALM risk model. From relation (2.23), it
follows that:
( ( )) ( ( ))
.
CL CL
E
tEuctUt
uct t
α
λβ
=
+−
=+ −
(2.25)
For the variance, we obtain:
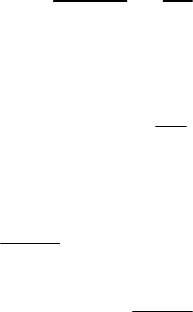
Insurance risk models 305
2
var( ( )) var( ( ))
.
CL CL
tUt
t
α
λα
=
=
(2.26)
For the ALM risk model, we have:
() () (),
ALM
tuAtBt
α
=
+−
(2.27)
and consequently:
22
(()) ( ),
var( ( )) ( ) .
ALM A B
ALM A B
E
tu t
tt
α
μμ
ασσ
=
+−
=+
(2.28)
Remembering that (1 ),c
λ
βη
=+ the method of moments for the adjustment of
these two models gives, with relations (2.25), (2.26) and (2.28), the following
conditions:
22
2
,
.
AB
AB
λ
βη μ μ
λ
ασσ
=
−
=+
(2.29)
The key parameter (2.21) is given by:
22
2
22.
AB
AB
R
μ
μ
β
η
σ
σα
−
==
+
(2.30)
From result (2.20), we can now propose an approximation value for the ruin
probability
()
CL
u
ψ
which is given by:
2
() exp 2
CL
uu
βη
ψ
α
⎛⎞
−
⎜⎟
⎝⎠
. (2.31)
Of course, this approximation will be reliable only if the ALM risk model fits
well the G/P considered model.
Substituting the value of
c
λ
β
η
λ
β
−
=
in this last result, we get:
2
() exp 2
CL
c
uu
λβ
ψ
λα
⎛⎞
−
−
⎜⎟
⎝⎠
. (2.32)
We see that the approximation (2.31) is equivalent to the approximation using
inequality (1.109), showing so that the approximation with the ALM-like model
gives a lower bound of
ψ
.
2.4 The Second ALM-Like Risk model
In the first ALM-like model, it is possible to have negative values for the asset
and liability values. To avoid this eventuality, we will start with a new model
called the second ALM-like Risk model or model ALM II based on the following
stochastic differential equations under the same assumptions as for the first
ALM-like model, called now ALM I but with dependence between the
considered Brownian motions.

306 Chapter 7
''
,
AA AA
dA A dt A dW A dZ
μσ β
=+ + (2.33)
''
,
B
BBB
dB B dt B dW B dZ
μσ β
=+ + (2.34)
where
(i)
W=(W(t), t
≥
0) is a standard Brownian motion,
(ii)
''
'( (), (), 0)
AB
ZZtZtt=≥ is a two-dimensional standard Brownian motion with
as covariance matrix:
1
,1,
1
ρ
ρ
ρ
⎡⎤
=
≤
⎢⎥
⎣⎦
M (2.35)
(iii) the processes W and '
Z
are independent,
(iv)
0000
(0) , (0) , ,AABBAB==>
(2.36)
(v)
μ
A,
μ
B,
σ
A
'
,
σ
B
'
are non-negative parameters.
Without loss of generality, the model (2.33), (2.34) can be replaced by the
following one:
,
,
AAA
B
BB
dA A dt A dZ
dB B dt A dZ
μ
σ
μσ
=
+
=+
(2.37)
where
2'22
2'22
,
,
AAA
B
BB
σ
σβ
σ
σβ
=+
=+
(2.38)
,
A
B
Z
Z being two standard Brownian motions with M as correlation coefficient.
With the result (4.20) of Chapter 5, we get:
0
0
()
exp( ( ))
()
A
At
tWt
Bt B
μσ
=+
(2.39)
with
0
0
()
exp( ( ))
()
A
At
tWt
Bt B
μσ
=+
, (2.40)
22
1
(),
2
AB AB
μ
μμ σσ
=−− −
(2.41)
222
2.
AB AB
σ
σσ ρσσ
=+− (2.42)
Let us remark that, theoretically, the risk component disappears when
,1
AB
σ
σρ
==. Of course, this case never occurs in practice but it means that the
management of the company must tend toward this result if they want to
minimize the risk.
As before we can study the lifetime of the company T, here defined as the first
value of t such that A(t) < B(t), or equivalently such that the process
()
ln , 0
()
At
t
Bt
⎛⎞
≥
⎜⎟
⎝⎠
(2.43)
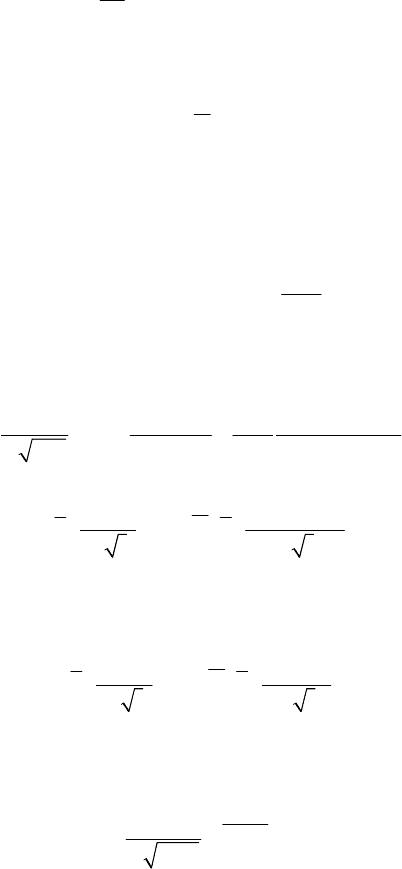
Insurance risk models 307
hits −∞,0
(
)
.
We can thus write:
0
0
inf{ ( ) },
ln .
TttWta
A
a
B
μσ
=−− >
=
(2.44)
Using the result of section 2.1, we get:
2
2
1, 0,
()
,0.
a
PT
e
μ
σ
μ
μ
−
≤
⎧
⎪
<∞ =
⎨
⎪
>
⎩
(2.45)
We can also get results for the following probability:
(,) ( , () ), ,
() ().
Pxt PT tMt x x a
Mt t Wt
μσ
=
>≤<
=− −
(2.46)
We can also write:
()
(,) ( , () ), ), .
()
ax
At
Pxt PT te Mt x x x a
Bt
−
=> < ≤< < (2.47)
Cox and Miller (1965) proved that
(,) ( ,)
x
Pxt pytdy
−∞
=
∫
, (2.48)
22
22 2
1()2(2)
(,) exp
22
2
yt ayat
pyt
tt
t
μμ μ
σσ σ
σπ
⎡
⎤
+−+
=−−
⎢
⎥
⎣
⎦
(2.49)
and by integration:
2
2
2
(,)
a
x
txat
Pxt e
tt
μ
σ
μ
μ
φφ
σσ
−
+−+
⎛⎞ ⎛ ⎞
=−
⎜⎟ ⎜ ⎟
⎝⎠ ⎝ ⎠
. (2.50)
Here, the non-ruin probability ( , )at
φ
on [0,t] is given by:
(,) (,)at Pat
φ
=
(2.51)
and so
2
2
(,)
a
at at
at e
tt
μ
σ
μ
μ
φφ φ
σσ
−
+−+
⎛⎞ ⎛ ⎞
=−
⎜⎟ ⎜ ⎟
⎝⎠ ⎝ ⎠
(2.52)
for which we get result (2.44), letting t →∞.
When the ruin is certain on an infinite horizon, that is iff 0
μ
≤
, T has the
following density:
2
2
()
2
3
() ,
2
at
t
T
a
ft e
t
μ
σ
σπ
+
−
= (2.53)
called an inverse Gaussian distribution for which it can be proved that
