Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.

268 Chapter 6
Table 5.6
reports the unconditional mean sojourn times, with the year as time
unit.
1 2 3 4 5
2.008219 3.353425 3.342466 3.465753 3.326027
Table 5.6:unconditional mean sojourn times
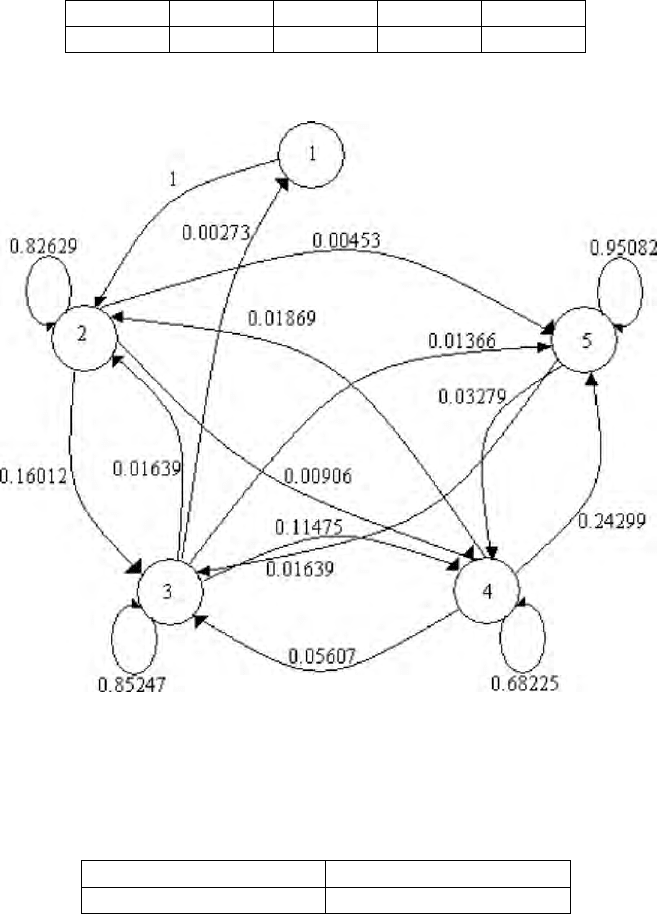
Figure 5.1: P-weighted transition graph
The last table of this section reports the asymptotic mean degrees obtained
respectively using Markov and semi-Markov models, the results already given in
the previous subsection.
Markov Semi-Markov
82.8533 82.75804
Table 5.7: asymptotic mean degrees
Finance and Insurance models 269
6 SEMI-MARKOV REWARD MULTIPLE-LIFE
INSURANCE MODELS
In this part, we present three different models for insurance applications.
The first two examples concern the topic of multiple life problems and are strictly
connected with pension scheme problems.
These two examples are given to show how to write the related formulas and to
attempt a first easy approach to pension scheme problems; for these reasons we
do not tackle in this case the problem of input data.
The third example is a real-life case concerning the evolution of a disability
illness. It is similar to the example developed in the previous section but the data
are different and the example will be developed without using, as previously, a
negative exponential increasing d.f. but with the distribution functions directly
obtained from the observed data, and furthermore, we use the reward model.
The results will be the RMPV and the rewards in this case will be only of
permanence type.
The first example will describe a two-life annuity example.
The typical case is the one of a retired person who can leave his/her pension to
the spouse.
Though we want to introduce the age dependence of the pensioners in addition to
the duration of pension, we will begin the simpler case of fixed death
probabilities to develop the topic thoroughly in the non-homogeneous case.
In the non-homogeneous environment it is possible to take into account many
aspects of pension schemes. Furthermore, as we will show in the last chapter, the
extension of the non-homogeneous case gives the possibility to consider all the
relevant aspects of pension schemes.
First we describe the model by means of a graph. This graphical approach was
described in Manca (1988).
Figure 6.1 reports the multiple state graph related to our example. The states of
the system are the following:
rs – state in which both the insured, retired and spouse, are living (state 1)
r – state in which only the direct pensioner is living (state 2)
s – state in which only the spouse is living (state 3)
d – state in which both the insured are dead (state 4).
The transition probabilities of the embedded Markov chain are:
rs
p
- probability of surviving of both the insured
r
p
- probability of surviving of direct pensioner
s
p
- probability of surviving of the spouse
rs
q - probability of dying in the same period of both the insured persons
r
q - probability of dying of direct pensioner
s
q
- probability of dying of the spouse.

270 Chapter 6
Figure 6.1: two-life annuity
The embedded Markov chain has the following form:
00
00
0001
rs s r rs
rr
s
s
p
qqq
p
q
p
q
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
P
. (6.1)
In the non-homogeneous case, the MC matrix structure is similar and the only
difference is that the non-zero elements will be time dependent.
The ( )
ij
F
t and ( , )
ij
F
st could be constructed by the available data.
In this case the rewards are only of the permanence type and transition rewards
make no sense.
We suppose that permanence rewards will be constant in time and are paid at the
end of the period, and also that the intensity of interest rate is fixed.
Under all these assumptions, it is possible to write the reward evolution equations
in both the homogeneous and non-homogeneous cases as follows:
Finance and Insurance models 271
()
4
11111
0
1
3
1
0
1
() 1 () ( )
() ( ) ,
t
k
t
k
t
kk
k
Vt Ht a Q a d
QeVtd
δϑδ
δϑ
ψ
ϑψϑ
ϑϑϑ
=
−
=
=− +
+−
∑
∫
∑
∫
(6.2)
()
4
11111
1
3
()
1
1
(,) 1 () (, )
(, ) ( ,) ,
t
k
ts s
s
k
t
s
kk
s
k
Vst Ht a Q s a d
Qs e V td
δϑδ
δϑ
ψ
ϑψϑ
ϑϑϑ
−−
=
−−
=
=− +
+
∑
∫
∑
∫
(6.3)
()
4
22222
0
2
22 2
0
() 1 () ( )
() ( ) ,
t
k
t
k
t
Vt H t a Q a d
QeVtd
δϑδ
δϑ
ψ
ϑψϑ
ϑϑϑ
=
−
=− +
+−
∑
∫
∫
(6.4)
()
4
22222
2
()
22 2
(,) 1 (,) (, )
(, ) ( ,) ,
t
k
ts s
s
k
t
s
s
Vst H st a Q s a d
Qs e V td
δϑδ
δϑ
ψ
ϑψϑ
ϑϑϑ
−−
=
−−
=− +
+
∑
∫
∫
(6.5)
()
4
33333
0
3
33 3
0
() 1 () ( )
() ( ) ,
t
k
t
k
t
Vt H t a Q a d
QeVtd
δϑδ
δϑ
ψ
ϑψϑ
ϑϑϑ
=
−
=− +
+−
∑
∫
∫
(6.6)
()
4
33333
3
()
33 3
(,) 1 (,) (, )
(, ) ( ,) .
t
k
ts s
s
k
t
s
s
Vst H st a Q s a d
Qs e V td
δϑδ
δϑ
ψ
ϑψϑ
ϑϑϑ
−−
=
−−
=− +
+
∑
∫
∫
(6.7)
Relations(6.2) and (6.3) give the mean present value of all the rewards received
by the system starting at time 0 or at time s from state 1 (both the insured are
living at the given time). The sum of the last elements rises to three because the
absorbing state doesn’t give any benefit.
Relations (6.4), (6.5) and (6.6), (6.7) are similar to the previous ones. They give
the mean present value of the rewards received starting at time 0 or s respectively
from state 2 or 3. From both these states the only real transition is with state 4
(dead state).
The formulas take into account this property and the last element takes into
account the only transition that is possible, the virtual one.
The next example will take into account a three-life model.
In this case, the example could be a pension to a family composed of three
members, the direct pensioner, her/his spouse and their child. The child will be in
the position to get the pension up to the end of his life (disabled child).
Figure 6.2 reports the multi-state graph related to this problem with as states:
272 Chapter 6
rsc – state in which all the insured are living (state 1)
rs – state in which the pensioner and the spouse are living (state 2)
sc – state in which the spouse and the child are living (state 3)
rc – state in which pensioner and the child are living (state 4)
r – state in which only the direct pensioner is living (state 5)
s – state in which only the spouse is living (state 6)
c – state in which the child is living (state 7)
d – state in which all the insured are dead (state 8).
The transition probabilities of the embedded Markov chain are:
rsc
p
- probability of surviving of all the insured people
rs
p
- probability of surviving of the pensioner and the spouse
s
c
p
- probability of surviving of the spouse and the child
rc
p
- probability of surviving of the pensioner and the child
r
p
- probability of surviving of direct pensioner
s
p
- probability of surviving of the spouse
c
p
- probability of surviving of the child
rsc
q - probability of dying of all the insured people
rs
q - probability of dying in the same period of both the insured persons
s
c
q
- probability of dying of the spouse and the child
rc
q - probability of dying of the pensioner and the child
r
q - probability of dying of direct pensioner
s
q
- probability of dying of the spouse.
c
q - probability of dying of the child
The homogeneous transition matrix of the embedded Markov chain is the
following:
000 0
00 00
000 0
0000 00
00000 0
000000
00000001
rsc c r s sc rc rs rsc
rs s r rs
s
ccssc
rc c r rc
rr
ss
cc
p
qqqqqqq
p
qq q
p
qqq
p
qqq
p
q
p
q
p
q
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
P
. (6.8)

Finance and Insurance models 273
Figure 6.2: three-life annuity graph
In the non-homogeneous case, the MC matrix structure is similar and the only
difference is that the non-zero elements will change because of time.
As before we do not enter into the details for the construction of ( )
ij
F
t and
(,)
ij
F
st .
We suppose that permanence rewards will be variable in time and will be paid at
the end of the period and also that the intensity of the interest rate is fixed.
Now we can write the related CTHSMRW and CTNHSMRW evolution
equations:
274 Chapter 6
()
111
0
87
11 1
11
00 0
() 1 () ( )
() () () ( ) ,
t
tt
kkk
kk
Vt H t e d
QeddQeVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑ ϑ
−
−−
==
=−
++−
∫
∑∑
∫∫ ∫
(6.9)
()
()
111
87
() ()
11 1
11
(,) 1 (,) (, )
() (,) (,) (,) ,
t
s
s
tt
ss
kkk
kk
ss s
Vst H st s e d
QseddQseVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−−
−− −−
==
=−
++
∫
∑∑
∫∫ ∫
(6.10)
()
222
0
87
22 2
22
00 0
() 1 () ( )
() () () ( ) ,
t
tt
kkk
kk
Vt H t e d
QeddQeVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−
−−
==
=−
++−
∫
∑∑
∫∫ ∫
(6.11)
()
()
222
87
() ()
22 2
22
(,) 1 (,) (, )
(, ) (, ) (, ) ( ,) ,
t
s
s
tt
ss
kkk
kk
ss s
Vst H st s e d
Qs s e dd Qs e V td
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−−
−− −−
==
=−
++
∫
∑∑
∫∫ ∫
(6.12)
()
333
0
87
33 3
33
00 0
() 1 () ( )
() () () ( ) ,
t
tt
kkk
kk
Vt Ht e d
QeddQeVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑ ϑ
−
−−
==
=−
++−
∫
∑∑
∫∫ ∫
(6.13)
()
()
333
87
() ()
33 3
33
(,) 1 (,) (, )
(, ) (, ) (, ) ( ,) ,
t
s
s
tt
ss
kkk
kk
ss s
Vst H st s e d
Qs s e dd Qs e V td
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−−
−− −−
==
=−
++
∫
∑∑
∫∫ ∫
(6.14)
()
444
0
87
44 4
44
00 0
() 1 () ( )
() () () ( ) ,
t
tt
kkk
kk
Vt H t e d
QeddQeVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−
−−
==
=−
++−
∫
∑∑
∫∫ ∫
(6.15)
Finance and Insurance models 275
()
()
444
87
() ()
44 4
44
(,) 1 (,) (, )
(, ) (, ) (, ) ( ,) ,
t
s
s
tt
ss
kkk
kk
ss s
Vst H st s e d
Qs s e dd Qs e V td
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−−
−− −−
==
=−
++
∫
∑∑
∫∫ ∫
(6.16)
()
555
0
8
55 55 5
5
00 0
() 1 () ( )
() () () ( ) ,
t
tt
k
k
Vt Ht e d
QeddQeVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑ ϑ
−
−−
=
=−
++−
∫
∑
∫∫ ∫
(6.17)
()
()
555
8
() ()
55 55 5
5
(,) 1 (,) (, )
(, ) (, ) (, ) ( ,) ,
t
s
s
tt
ss
k
k
ss s
Vst Hst s e d
Qs s e dd Qs e V td
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−−
−− −−
=
=−
++
∫
∑
∫∫ ∫
(6.18)
()
666
0
8
66 66 6
6
00 0
() 1 () ( )
() () () ( ) ,
t
tt
k
k
Vt H t e d
QeddQeVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑ ϑ
−
−−
=
=−
++−
∫
∑
∫∫ ∫
(6.19)
()
()
666
8
() ()
66 66 6
6
(,) 1 (,) (, )
(, ) (, ) (, ) ( ,) ,
t
s
s
tt
ss
k
k
ss s
Vst Hst s e d
Qs s e dd Qs e V td
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−−
−− −−
=
=−
++
∫
∑
∫∫ ∫
(6.20)
()
777
0
8
77 77 7
7
00 0
() 1 () ( )
() () () ( ) ,
t
tt
k
k
Vt H t e d
QeddQeVtd
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑ ϑ
−
−−
=
=−
++−
∫
∑
∫∫ ∫
. (6.21)
()
()
777
8
() ()
77 77 7
7
(,) 1 (,) (, )
(, ) (, ) (, ) ( ,) .
t
s
s
tt
ss
k
k
ss s
Vst H st s e d
Qs s e dd Qs e V td
δθ
ϑ
δθ δϑ
ψθ θ
ϑ
ψθ θϑ ϑ ϑϑ
−−
−− −−
=
=−
++
∫
∑
∫∫ ∫
(6.22)
From the graph depicted in
Figure 6.2, each node constitutes an equivalence
class and the equivalence classes are:
276 Chapter 6
{
}
{
}
{
}
{
}
{
}
{
}
{
}
{
}
12345678
,,,,,,,.CrscCrsCscCrcCrCsCcCd========
Class
1
C is the only maximal class and
8
C the only minimal (absorbing,
essential) class and all the other classes are transient.
For these reasons once the system is in a state, it cannot come back.
In the formulas the sum starts always from the initial state.
For obvious reasons, the absorbing state does not make any contribution to the
rewards, and is not considered in the last part of each formula.
In the last six formulas it results that for the starting state the only real transition
is with state 8 (death state). The formulas take into account this property and the
last element takes into account the only transition that is possible, the virtual one.
7 INSURANCE MODEL WITH STOCHASTIC
INTEREST RATES
7.1 Introduction
In this section we apply homogeneous or non-homogeneous semi-Markov
rewards to the actuarial field using a stochastic term structure of implied forward
rates.
To apply the model, first it is necessary to solve the semi-Markov evolution
equation to get the stochastic interest rates problem as presented in section 3 and
then we have to solve the related homogeneous semi-Markov reward process.
In the homogeneous reward case the semi-Markov interest model should be
homogeneous; however in the non-homogeneous case we can have a
homogeneous or non-homogeneous semi-Markov interest rate model.
In the non-homogeneous case only the non-homogeneous interest rate model will
be presented.
The reward process will be extended with the introduction of stochastic interest
rates.
7.2 The Actuarial Problem
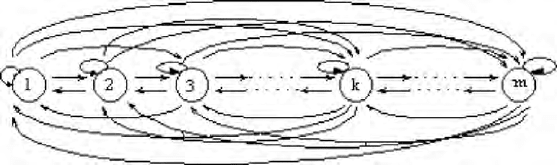
We now consider a model with m states presented in the graph of Figure 7.1.
It must be made clear that the arcs depict all possible transitions; they are
weighted and their weights represent the transition probabilities and the rewards
that are paid in the case of transition on the arc.
The weights will be represented by a pair (p,r) where p represents the probability
and r the related reward, which can be a positive or negative value, depending on
whether it is respectively an entrance or a payment.
If p is equal to 0, then r must be 0 because if it is not possible to cross the arc the
related reward is meaningless.
Finance and Insurance models 277
Furthermore, the nodes representing the model states are also weighted and their
weights represent the permanence reward paid or received remaining in the
considered state.
Figure 7.1: m states model for insurance models.
All rewards can be fixed or can change during the time evolution of the model.
The different models can be constructed giving different values for p. For
example if a node has all the probabilities of leaving the related state equal to 0,
then this will be an absorbing state.
7.3 A Semi-Markov Reward Stochastic Interest Rate Model
A stochastic term structure of implied forward rates can be constructed by means
of SMP in both homogeneous and non-homogeneous cases, as explained before.
As usual the evolution equation of the DTSMP will be the following one:
11
() (1 ()) ( ) ( ),
nt
ij ij i j i
tHt tb
ββ
βϑ
φ
δφϑϑ
==
=− + −
∑∑
(7.1)
11
(,) (1 (,)) ( ,) (, ),
nt
ij ij i j i
s
st H st tb s
ββ
βϑ
φ
δφϑϑ
==+
=− +
∑∑
(7.2)
where ( )
ij
t
φ
and ( , )
ij
s
t
φ
represent, as already said, the probability that at time t
the implied interest rate will be
j
r given that the implied interest rate was
i
r at
time 0 in the homogeneous case and s in the non-homogeneous. We suppose that
the states of interest rate model are:
{
}
12
,, , .
n
E
rr r
=
… (7.3)
The related mean discount factors at time h are constructed as explained in
section 3.
More precisely ( )h
ε
ν
and ( , )
s
h
ε
ν
represent the mean discounting factor for a
time h given that at epoch 0 (s) the interest rate was r
ε
.
The states of the reward process are always
{
}
12
,,,
m
ISS S
=
… (7.4)
